教学考试杂志社“优师计划”阶段性成果展示——“电磁学”相关试题选登

一、电场

【例1】如图所示，两块长度均为L的带电平行板水平放置，两板之间距离为d。当两平行板之间的电压为U时，一带电荷量为q的小球以速度v恰好能够沿两平行板之间的中心线做匀速直线运动，下列说法正确的是

( )

【例2】如图所示的匀强电场中，A、B、C、D、E、F是一边长为5 cm的正六边形的顶点，已知A、C、D三点电势分别为15 V、10 V、5 V。关于该匀强电场的场强，下列说法正确的有

( )

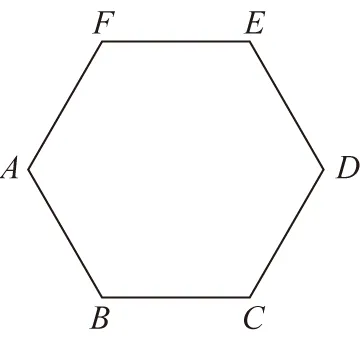
A.电场方向沿AD连线指向D，场强大小为100 V/m

B.电场方向沿AD连线指向A，场强大小为100 V/m

二、磁场

( )

A.该带电粒子带负电

D.若将入射点D稍向A点移动，其在磁场中运动的时间变长

( )

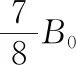
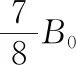
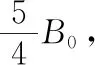
【例3】轻质绝缘的细线一端连接固定的悬点O，另一端系在匀质导体棒的重心(几何中心)。假设导体棒垂直放在水平向左的匀强磁场中，电流向里保持不变，导体棒在重力、安培力的作用下正好保持平衡状态，此位置细线水平，正好伸直但无拉力。现让匀强磁场的方向沿逆时针缓慢转动，方向由水平向左缓慢变成水平向右，保持磁感应强度的大小不变，在此过程中导体棒也缓慢的下降，悬线也缓慢的转动。认为导体棒始终处于平衡状态。有关悬线拉力的大小、方向的变化，下列说法正确的是

( )

A.当匀强磁场的方向沿逆时针缓慢旋转的角度为α时，悬线绕O点旋转的角度也为α

C.匀强磁场的方向沿逆时针由水平向左缓慢变成水平向右的过程中，悬线的拉力先变大后变小

D.匀强磁场的方向沿逆时针由水平向左缓慢变成水平向右的过程中，悬线的拉力不可能等于重力的2倍

( )

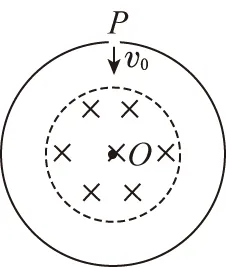
A．粒子与壁槽碰撞次数一定是奇数次

B．粒子与壁槽碰撞次数一定是偶数次

D．若粒子与壁槽撞击四次，则粒子的运动路径只有唯一可能

( )

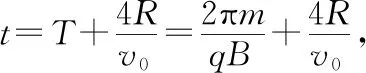
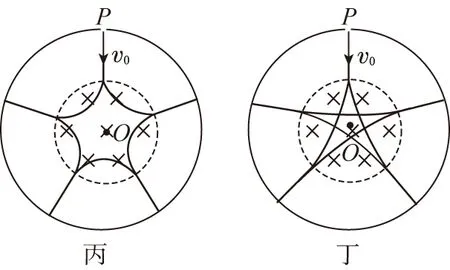
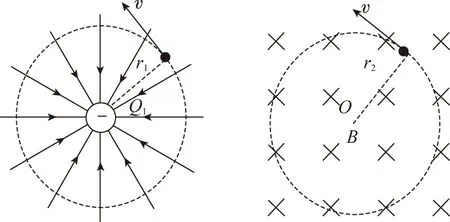
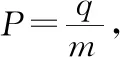
【例6】如图所示，在边长为l的菱形ACDE中分布着磁感应强度为B的匀强磁场，磁场方向垂直纸面向外，且∠A=60°。在菱形的对角线CE的中点P有一粒子放射源，可以向各个方向释放不同速率的电子，电子带电荷量为e，质量为m。

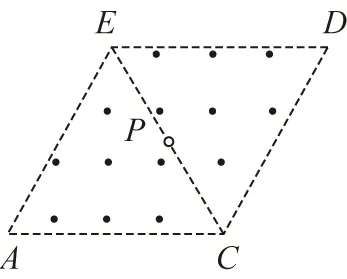
(1)若所有电子都能在菱形磁场内运动，不会射出菱形磁场区域，求电子的最大速率v0；

(2)若电子以4v0向各个方向发射，求电子到达AC边的最长时间。

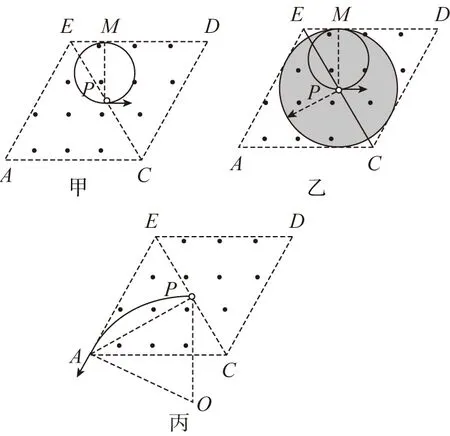
【解析】(1)所有电子不会射出菱形磁场区域，临界状态如图甲所示，粒子能够到达区域如图乙所示。

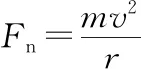
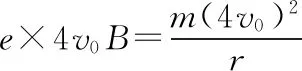
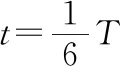
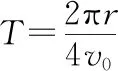
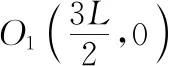
(1)电场强度的大小；

(2)电场强度与磁感应强度的大小之比；

(3)带电粒子从进入磁场到离开电场所用的时间。

【解析】(1)如图所示，将带电粒子的运动过程逆向处理，带电粒子在电场中做类平抛运动时，设其竖直分位移为y，设合位移与水平方向之间的夹角为α，粒子射出电场时的速度与水平方向之间的夹角为β，由类平抛运动的规律得

L=v0t1①

vx=v0④

vy=at1⑤

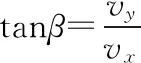
联立①②③④⑤⑥解得tanβ=2tanα⑦

由几何关系得

由牛顿第二定律得qE=ma⑩

(2)带电粒子在磁场中运动的速率为

由几何关系知，带电粒子在磁场中运动时的轨道半径为

(3)带电粒子做匀速直线运动的时间为

带电粒子在磁场中运动的时间为

带电粒子从进入磁场到离开电场所用的时间为

三、电磁感应

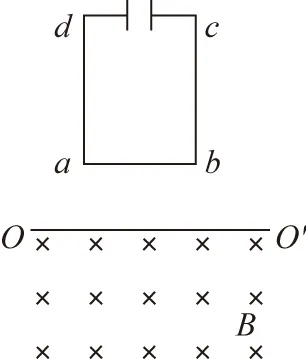
【例1】如图所示，空间中存在垂直纸面向里的匀强磁场(磁场区域足够大)，磁场的上边界为水平线OO′，现将一个接有电容器且不计电阻的矩形线圈从水平线OO′上方的某点由静止释放，设线圈下落过程中的速度为v，加速度为a，已知电容器的初始电荷量为零，电容器可以容纳足够多的电荷。设ab边进入磁场的时刻为t1，cd边进入磁场的时刻为t2。下列图象能正确反映线圈在这段时间内运动规律的是

( )

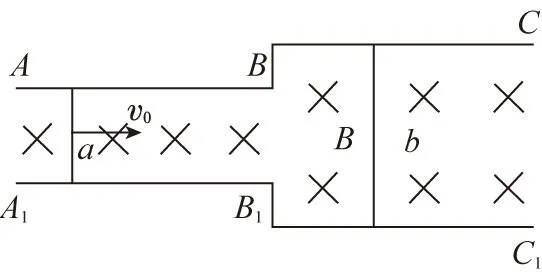
【例2】两根相互平行、足够长光滑金属导轨ABC-A1B1C1固定于水平桌面，左侧AB-A1B1轨道间距为L，右侧BC-B1C1轨道间距为2L，导轨所在区域存在垂直桌面竖直向下的匀强磁场，磁感应强度大小为B。如图所示，两横截面积相同、由同种金属材料制成的导体棒a、b分别置于导轨的左右两侧，已知导体棒的长度均略大于导轨间的距离，导体棒a的质量为m。某时刻导体棒a获得一个初速度v0开始向右运动,导体棒始终垂直于导轨且与导轨接触良好。不计导轨电阻，关于导体棒以后运动，下列说法正确的是

( )

A．导体棒a、b稳定运动后，相等时间通过的位移之比是 2∶1

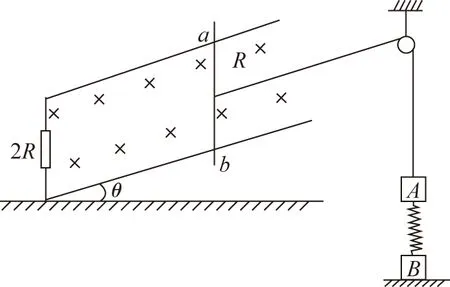
【例3】如图所示，倾角为θ的斜面处于垂直斜面向下的匀强磁场中，磁感应强度大小为B，斜面上固定有两光滑平行导轨，两导轨足够长且电阻不计，导轨间的距离为L，并且在导轨下端连有一阻值为2R的电阻。物体A、B的质量为m，用一根轻弹簧连接，物体A与导体棒ab通过一根绕过光滑定滑轮的轻绳连接，导体棒ab的质量是10m，在外力作用下静止在斜面上，开始的时候绳子刚好伸直但不受力，A、B处于静止状态，弹簧劲度系数为k，现无初速度释放电阻为R的导体棒ab，当物体B恰好离开地面时，导体棒ab的加速度恰好为零，重力加速度为g，求：

(1)从ab开始运动到物体B刚好离开地面的过程中，流过电阻的电荷量为多少？

(2)从ab开始运动到物体B刚好离开地面的过程中，导体棒ab产生的热量是多少？

(3)物体B刚好离开地面时剪断轻绳，若从剪断轻绳到导体棒再次加速度为零时，导体棒ab向下移动了x，求这一过程所经历的时间。

【解析】(1)开始时弹簧处于压缩状态

由mg=kΔx1

同理，物体B刚离开地面时，弹簧的伸长量

故此时导体棒ab沿斜面向下运动了

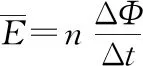
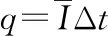
(2)物体B对地面压力为零时，导体棒ab的加速度恰好为零，由10mgsinθ=BIL+2mg

E=BLv

由能量守恒定律得

整理得

(3)剪断细线后，棒开始做加速运动，再次达到匀速时，有10mgsinθ=BI′L

E′=BLv′

对棒，取一小段时间Δt，由动量定理有

10mgsinθ·Δt-BI1LΔt=mv1-mv

10mgsinθ·Δt-BI2LΔt=mv2-mv1

10mgsinθ·Δt-BI3LΔt=mv3-mv2

……

左右各相加得10mgsinθ·t-BLq′=mv′-mv