形异质同——“人船模型”的应用

江西 郭春文

“人船模型”不仅是动量守恒定律的典型模型，也是非常重要的力学综合模型。它伴随着力学与运动过程的发生、发展和变化，解决此类问题常利用微元法，而微元法的思想也是高中物理的难点之一，直接影响动力学问题的分析思路，通过“人船模型”的学习，可以使许多动量守恒问题迎刃而解。

一、构建“人船模型”

两个原来静止的物体发生相互作用时，若所受外力的矢量和为零，则系统动量守恒。在相互作用的过程中，任一时刻两物体的速度大小之比等于质量的反比，这样的问题归为“人船模型”问题。

【例1】如图1所示，质量为M的船停在静止的水面上，船长为L，一质量为m的人，由船头走到船尾，若不计水的阻力，求整个过程人和船相对于水面移动的距离。

图1

【解析】“人船模型”是人与船构成的系统，由于系统受力平衡，故人和船组成的系统动量守恒。在人和船运动过程中，以水面为参考系，设任意时刻人的速度大小为v1i，船的速度大小为v2i，由于人和船组成的系统任意时刻所受合力都为零，故任意时刻都满足动量守恒定律。

对人和船组成的系统，以向右为正方向，根据动量守恒定律得0=mv1i-Mv2i

两边乘以Δti得0=mv1iΔti-Mv2iΔti

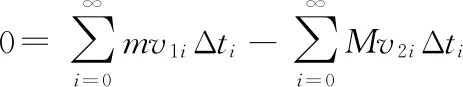
则mx1-Mx2=0

而x1+x2=L

【易错点分析】首先，从“人船模型”过程来看，人动船动，人快船快，人慢船慢，人右船左，不能简单地理解为人匀速向右运动，要体现微元法的思想；其次，“人船模型”属于动量守恒定律的运用，要注意其矢量性、相对性；最后，解题的要画人和船的过程图，在此过程中人相对地面向右运动，船向左运动，由于运动具有独立性，人的位置在出发点的右侧，船的位置在出发点的左侧。

【例2】如图2所示，长为L，质量为M的小船停在静水中，船头与船尾分别站立质量为m1、m2(m1>m2)的两个人，那么，当两个人互换位置后，船在水平方向移动了多少距离？

图2

【解析】本题是“人船模型”的应用，两个人和船构成一个系统，系统受力平衡，故系统动量守恒。在人和船运动过程中，以水面为参考系，由于两个人相向运动，根据人船模型结果可知，人船模型中人与船的位移之比与速度大小无关，则可以认为左右两边质量均为m2的人保持静止，即等效于是一个质量为Δm=m1-m2的人从左向右运动，船的质量变为M′=M+2m2，设人的速度大小为v1i，船的速度大小为v2i。

对人和船组成的系统，以向右为正方向，由动量守恒定律得0=Δmv1iΔti-(M+2m2)v2iΔti

两边求和得(m1-m2)x1-(M+2m2)x2=0

而x1+x2=L

【易错点分析】首先，本题为“人船模型”的拓展应用，题中两个人在船上相向运动，涉及三个物体运动的问题，多对象问题是一个难点，较难分析清楚对应的具体物理过程及解题思路；其次，两人相向运动，可以看成两人先后运动求解，此方法虽然可以解题，但是过程和计算都比较麻烦，考试中会浪费大量时间。

【点评】本题主要考查多个物体的“人船模型”问题及其解题方法。题中人和船组成的系统动量守恒，两人相向运动，根据其模型结论，人和船位移与速度大小无关，只与质量有关，可以认为船两端质量为m2的人保持静止，与原来的船构成了一个新的船，质量为M′=M+2m2，相向运动中，两人等效于一个新的研究对象，质量为Δm=m1-m2，新的研究对象Δm和新的船M′组成新的人船模型，从而可以方便、快速求解。等效替代法是科学研究中常用的思维方法，掌握等效替代法及应用，体会物理等效思想的内涵，有助于提高考生的科学素养，初步形成科学的世界观和方法论，为终身的学习、研究和发展奠定基础。

二、“人船模型”变形一

滑块从光滑水平地面上的斜面滑下，与人船模型类似，滑块类似于人，小车类似于船，水平方向不受外力作用，水平方向动量守恒和系统机械能守恒，可以此来求水平速度以及水平位移。

【例3】如图3所示，质量为M的小车静止在光滑的水平面上，小车AB段是半径为R的四分之一光滑圆弧轨道，BC段是长为L的水平粗糙轨道，两段轨道相切于B点，一质量为m的滑块在小车上从A点由静止开始沿轨道滑下，然后滑入BC轨道，最后恰好停在C点。已知小车质量M=2m，滑块与轨道BC间的动摩擦因数为μ，重力加速度为g滑块可视为质点。则滑块从A运动到C的过程中

图3

( )

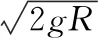
【解析】以滑块和小车为系统，当滑块m下滑的过程中，水平方向向右运动，小车向左运动，滑块重力势能转化为系统的动能。滑块m从A到C过程中，以向右为正方向，系统的水平方向动量守恒。

设滑块相对地面的位移大小为x，小车相对地面的位移大小为s，滑块和小车在水平方向上动量守恒。

由人船模型结论可得0=mx-Ms

x+s=R+L

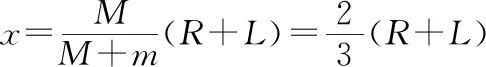
在滑块m从A到B过程中，小车速度一直在增大；滑块m从B到C过程中，小车速度一直在减小，故滑块运动到B点时，小车、滑块速度最大。

滑块m从A到B过程中，以水平向右为正，系统水平动量守恒、机械能守恒。

由水平方向动量守恒得0=mv1-Mv2

【点评】本题主要考查“人船模型”的变形——滑块从光滑圆弧轨道滑下，是水平动量守恒和机械能量守恒定律的共同运用。在下滑过程中，滑块对四分之一光滑圆弧轨道做正功，圆弧轨道速度增大，即滑块的重力势能转化为系统的总动能，要求学生选择恰当的初末状态，运用水平方向动量守恒和能量守恒解题，求出速度大小；通过类比人船模型寻找两者位移的几何关系，可求出各自位移大小。

【例4】如图4所示，光滑水平面上有一平板车，车上固定一竖直直杆，杆的最高点O通过一长为L的轻绳拴接一个可视为质点的小球，小球的质量与小车质量相等，悬点O距离地面的高度为3L，轻绳水平时，小球与小车速度均为零。释放小球，当小球运动到最低点时，轻绳断开，重力加速度为g。(小球在运动过程中与竖直直杆和小车不相撞)求：

图4

(1)轻绳断开的瞬间，小球的速度大小；

(2)小球从释放到落地的过程中，小车向右移动的距离。

【解析】(1)小球下落过程中，小球与车组成的系统，水平方向动量守恒，系统机械能守恒，设小球运动到最低点时，小球的速率为v1，小车的速率为v2。

设小球的速度方向为正方向，小球和车的质量均为m，则由水平方向应用动量守恒定律和机械能守恒定律可得

mv1-mv2=0

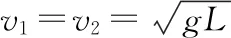
(2)小球下落的过程中，小球向左移动的距离为x1，车向右移动的距离为x2，则有

mx1-mx2=0

且x1+x2=L

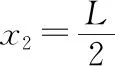
三、“人船模型”变形二

在人船模型中，应用动量守恒定律，要注意参考系的选取，没有特殊说明，一般以地面为参考系，即公式v1、v2、x和s一般都是相对地面而言的；当以其他物体为参考系时，要注意始末状态都应保持同一参考系。

【例5】如图5所示，气球质量为100 kg，载有质量为50 kg的人(可以把人看做质点)，静止在空中距地面20 m高的地方，气球下方悬一根质量可忽略不计的绳子，此人想从气球上沿绳慢慢下滑至地面，为了安全到达地面，则绳长至少应为

图5

( )

A.10 m B.30 m C.40 m D.60 m

【解析】人和气球组成的系统动量守恒，当人不动时，气球也不动；当人向下运动时，气球向上运动，且变化情况一致，根据动量守恒定律列出等式求解。

人与气球组成的系统动量守恒，设人的速度大小v1i，气球的速度大小v2i，设运动时间t，对人与气球组成的系统为研究对象，以向下为正方向，由动量守恒定律得

m1v1i-m2v2i=0

m1s1-m2s2=0

气球和人运动的路程之和为绳子的长度，则绳子长度l=s1+s2=30 m，故B正确，ACD错误。

【易错点分析】人与气球组成的系统动量守恒，人向下运动，气球向上运动，人相对地面向下运动了20 m，即x人=20 m，而人船模型中则是人相对船走了一个船长，此题中参考系发生了改变，应避免误用人船模型结论x人+x船=l。

【点评】本题主要考查动量守恒定律参考系的问题，关键是找出人和气球的速度关系和绳子长度与运动路程的关系。人和气球组成系统动量守恒，由于初始状态人距离地面高度为20 m，以地面为参考系，在人相对地面向下运动20 m到达地面，即x人=20 m.球向上运动，所以绳长应等于两者路程之和，而“人船模型”是人相对船运动的位移为船长，故在运用“人船模型”及其变式时应注意研究对象相对哪一参考系运动了多少距离；本题中假设人可以看成质点，如果不能看成质点，则要考虑其质心运动。

【例6】在光滑的冰面上停着一辆车，车上坐着一个人，还堆有2个质量均为m的沙袋，车、人及所有沙袋的总质量为M。若车上的人每次均将沙袋以相对于车大小为v的速率向后扔出，则在第2个沙袋扔出后，车速大小为

( )

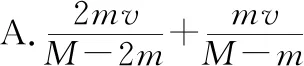
【解析】本题是动量守恒定律的直接应用，分别对两次扔沙袋列出系统动量守恒，以地面为参考系。

扔下第一个沙袋后瞬间，设车的速度为u1，根据系统动量守恒得

0=(M-m)u1+m(-v+u1)

扔下第二个沙袋后瞬间，设车的速度为u2，根据系统动量守恒得

(M-m)u1=(M-2m)u2+m(-v+u2)

【易错点分析】首先本题车、人及所有沙袋组成的系统动量守恒，以地面为参考系，而题中车上的人每次均将沙袋以相对于车大小为v的速率向后扔出，应先将沙袋相对于车大小为v的速率转化为相对于地面的速度，即v袋对地=v袋对车+v车对地，应注意速度与速率的区别；其次应同时考虑速度转换过程中速度的矢量性和同时性，即v袋对车、v车对地指的是同一时刻的速度。

【点评】本题是动量守恒定律的一个典型应用，重点考查转换参考系中速度矢量性和同时性问题。动量守恒定律一般以地面为参考系，题中车上的人每次均将沙袋以相对于车大小为v的速率向后扔出，以车的速度为正，应先将速率转化成以地面为参考系下的速度，vA对地=vA对B+vB对地，即题中v袋对地=-v+v车对地；其次特别要注意动量守恒的始末状态，相对车的速度指的是沙袋相对同一时刻(即同一状态)时车的速度，否则容易造成错选。

人船模型及其变形是动量守恒定律的重要运用，与机械能守恒定律、能量守恒定律的巧妙结合，使题目变化多样，学生应紧紧抓住这几大主线及其使用条件，弄清题中各物理量的物理意义，灵活运用物理规律，许多动量守恒问题便迎刃而解。