基于自适应模糊PID的爬壁机器人运动路径控制研究

苏 娜，张华胜，俞竹青

(常州大学机械工程学院，江苏 常州 213100)

0 引言

在大型发电供热企业中，由于锅炉壁面长期受到液体侵蚀、磨损，使壁厚变薄，所以需定期检测壁面磨损程度以保证锅炉的安全可靠[1]。目前，锅炉壁面磨损检测主要由人工搭建脚手架完成检测，而人工检测效率低，费用高且危险系数高，因此研制一种能自主检测壁面磨损的爬壁机器人是化工行业发展的趋势。

在锅炉内部，磨损检测机器人的移动作业环境较为复杂，确保爬壁机器人按照预定的轨迹爬行是完成壁厚检测任务的重点。机器人在正常工作爬行过程中，在理想情况下，控制左右两电机速度完全相同，则可以始终直线爬行。但实际上，由于制造误差以及环境等因素的影响，爬壁机器人的位姿会出现偏差，所以对其路径控制的研究是研究爬壁机器人的重点。针对路径控制的研究，相关学者根据具体情况提出了各自的解决方案。张扬名[2]等基于滑模控制方法来实现路径控制，但由于滑模控制方法的特性使其存在“抖振”，且无法避免，控制效果欠佳。李林琛[3]等通过遗传算法对比例积分微分(proportion integration differentiation，PID)参数整定来实现路径控制。但遗传算法编程比较复杂，需要较长时间的训练得到精确解。

针对上述问题，本文提出一种基于自适应模糊PID算法的运动路径控制方法，即根据爬壁机器人实时的位姿角度偏差对PID参数进行模糊化在线增量调节，以应对系统的实时变化。通过选择合适的参数对机器人左右电机速度进行模糊PID控制，进而控制机器人的运动方向，保证其运动的稳定性。通过MATLAB试验仿真，验证了该算法鲁棒性好、自适应性强，控制效果显著提升。该方法能够快速、准确地控制左右电机的转速，进而纠正机器人的位姿偏差，达到运动路径控制的目的。

1 爬壁机器人基本结构

本文研究的爬壁机器人由爬行驱动机构、超声波检测机构、磁吸附机构等组成，采用永磁吸附、链条式传动和电机驱动的机器人原理设计。

爬壁检测机器人静止时，通过履带上的永磁铁吸附在壁面。运动时，通过驱动电机正反转，经减速器减速后链轮转动，带动与之啮合的链条，使机器人沿着壁面上下爬行。

2 系统总体结构与运动学建模

建立爬壁机器人运动模型，系统结合倾角传感器和编码器测速传感器以及自适应模糊PID控制算法，实现爬壁机器人运动控制。

2.1 系统介绍

本文研究的基于STM32的爬壁机器人驱动控制系统，主要由电源、电机驱动、速度检测、位置检测等部分组成。爬壁机器人系统框架如图1所示。

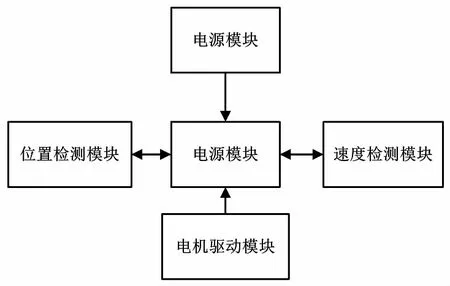
图1 爬壁机器人系统框架Fig.1 Framework of a wall-climbing robot system

爬壁机器人系统采用的是位置角度误差外环和速度误差内环的双闭环控制方式[4]，如图2所示。

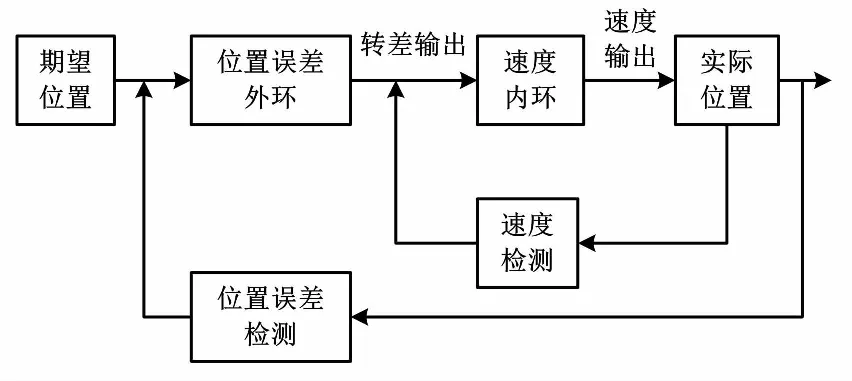
图2 双闭环控制方式Fig.2 Double closed-loop control mode

在爬壁机器人爬行过程中：首先，位置误差作为外环，通过倾角传感器不断获取位置角度偏差信息，进行外环位置误差的模糊 PID控制；其次，通过推导的运动学方程，得到转向的输出速度，转差给速度内环，利用速度闭环控制，检测实际运行速度，通过模糊PID控制算法对目标速度进行误差诊断；最后，控制脉冲宽度调制(pulse width modulation,PWM)不断调节电机转速，使爬壁机器人运动得到控制，更加快速、平稳地在双闭环系统下按照规定轨迹爬行，完成检测工作。

2.2 运动学建模

爬壁机器人运动分析如图3所示。

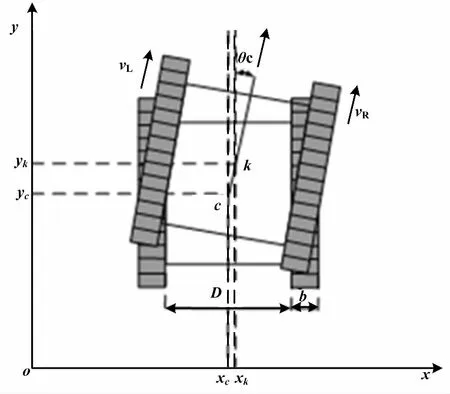
图3 爬壁机器人运动分析图Fig.3 Motion analysis diagram of wall-climbing robot

针对上述爬壁机器人，对其进行运动学分析，并建立爬壁机器人运动模型[5]，掌握其运动规律，为下文控制器的设计奠定基础。

设在XOY参考平面上，爬壁机器人以平行于规定轨迹L的位姿运动，左右履带的理论运动速度分别为vL和vR，合成速度为v，爬壁机器人的质心运动到C点(xc,yc)，倾斜角度为0°，则爬壁机器人的位姿表示为Pc=[xc,yc,0]T。当机器人继续向前运动，质心运动到K点，机器人的位姿表示为Pk=[xk,yk,θk]T。所以爬壁机器人位姿可由式(1)表示：

(1)

本文研究的爬壁机器人在其运动过程中几乎不发生滑动，即vL=vL′和vR=vR′，求得kL=kR=0。故可以将式(1)改写为：

(2)

在理想情况下，偏差角度始终保持在0°，移动速度vR=vL=v，对式(2)求导，得到爬壁机器人在理想情况下的运动学方程：

(3)

而实际上，两侧履带因制造差异及工作环境等因素的影响，速度无法完全一致，故机器人运动方向发生变化，位姿发生偏差。不妨假设其质心运动到K点时， 爬壁机器人倾斜角度为θk， 则可得到在K点时的动力学方程：

(4)

式中：D为两履带内侧的距离；d为履带的宽度。本文研究的爬壁机器人D=210 mm，d=45 mm。由运动学方程可知，爬壁机器人位姿偏差与左右履带运动速度和偏差角度之间的关系。

综上所述，爬壁机器人在运动过程中，可以通过对两侧驱动轮的速度vL和vR的差速控制，实现对机器人的运动速度和偏转角度的实时调节，得到位置误差外环的输出，进而实现爬壁机器人预期位置的调节。

3 控制器设计

3.1 控制结构

自适应模糊PID算法相较于普通PID的先进之处在于跟据系统的跟踪误差，运用模糊推理的策略对PID的3个参数进行实时调节[6]，以满足不同时刻的要求。这样既能够保持普通PID控制系统的简单易用的优点，又具备一定的自适应性，可进一步提高控制的精确性[7]。模糊PID控制器框图如图4所示。

图4 模糊PID控制器框图Fig.4 System diagram of fuzzy PID controller

模糊控制器的输入为系统设定的期望位置偏转角度，反馈值为传感器模块反馈得到的实际位置偏转角度。模糊系统的输入通过模糊推理，找出与输出的PID 3个参数的模糊关系，实时更改，使控制器具有一定的自适应能力和良好的控制效果。速度内环和位置误差外环的控制原理相似，下文控制器的设计以位置误差外环控制为例。

3.2 模糊化和隶属度函数

将位置误差外环的输入变量方向偏差θ和方向偏差变化率θc变化范围定义为模糊集上的论域[-30,30]，输出量Δkp、Δki、Δkd的论域为[-3,3]，模糊子集分别为{NB,NM,NS,ZO,PS,PM,PB},对应为{负大，负中，负小，零，正小，正中，正大}。考虑调节难易程度以及灵敏度的问题，以三角形函数建立隶属度函数[8]，隶属度函数如图5所示。

图5 隶属度函数Fig.5 Membership function

3.3 模糊控制规则

根据实际操作经验和相关的专业知识，建立合适的模糊规则[9]。本文根据Δkp、Δki、Δkd对系统的影响，采用条件语句if-then的推理规则，即：If (θis NB) and (θcis NM) then (Δkpis PB) (Δkiis NB) (Δkiis NS) ，得出相应的结果，如表1～表3所示。

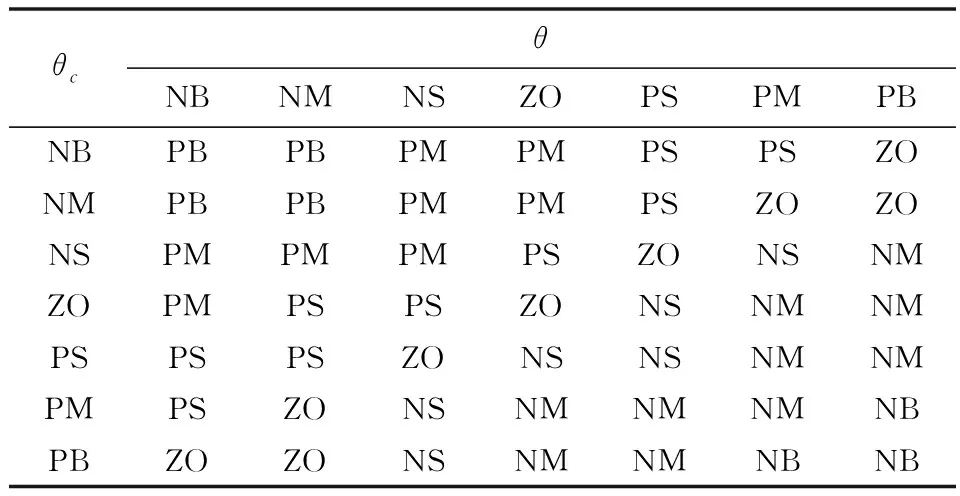
表1 Δkp模糊控制规则表Tab.1 Δkp fuzzy control rules table

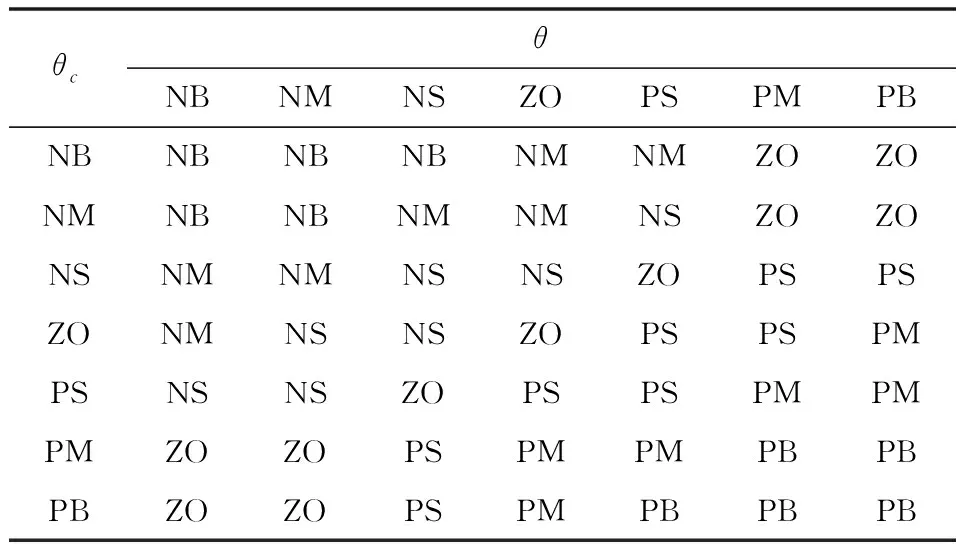
表2 Δki模糊控制规则表Tab.2 Δki fuzzy control rules table

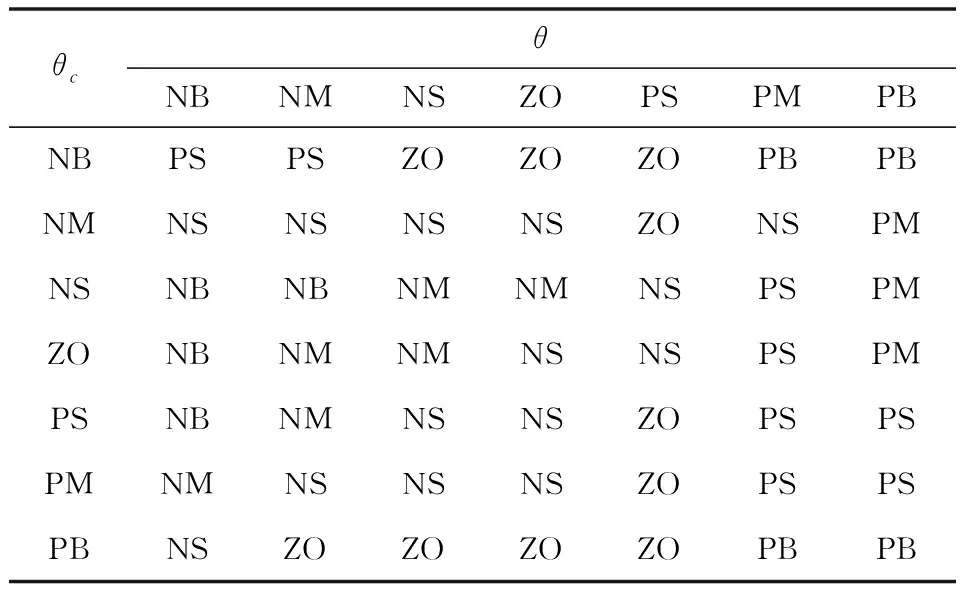
表3 Δkd模糊控制规则表Tab.3 Δkd fuzzy control rules table

3.4 最终参数整定

经过模糊推理规则得到的结果是一个模糊集，需要通过解模糊，将其转化成一个精确值后才能使用。本文采用加权平均法[10]，将控制量中的各元素和它对应的隶属度加权平均值，计算公式如式(5)所示：

(5)

式中:u′为解模糊后的精确值;ui为模糊变量的元素;μ(ui)为ui元素相对应的隶属度。

根据上文建立的模糊规则表，执行相应的运算，将结果转化处理后代入式(6)中，得出整定后的PID实际参数。

(6)

式中:kp′、ki′、kd′为PID的初始参数；Δkp、Δki、Δkd为模糊控制器根据系统的输入方向偏差θ和方向偏差变化率θc实时调节的增量；kp、ki、kd为系统最终整定的参数值。

PID参数实时改变体现了本文控制算法的自适应性。

4 Simulink仿真验证

为了验证自适应模糊PID算法对本文爬壁机器人运动路径控制的电机驱动的控制效果，爬壁机器人采用直流无刷电机驱动。通过相关软件，将传递函数简化为二阶系统[11]，表示为：

(7)

在Simulink中，根据上文研究分析的控制规则，建立控制器的仿真模型。

本文根据以往经验，通过不断的试验，得到一组比较合适的PID参数值:P=60，I=8，D=0.05。为了便于比较两种算法对输入信号的跟踪效果，将初始参数值设定为相同。试验过程中，在1 s时加入阶跃信号，两种控制算法的阶跃信号响应线和仿真数据对比如图6和表4所示。

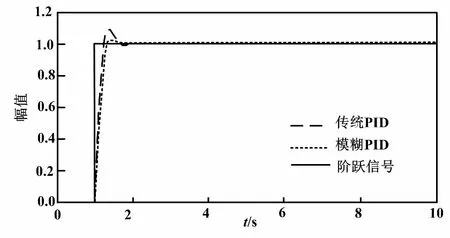
图6 阶跃信号响应曲线Fig.6 Step signal response curves

表4 仿真数据对比表Tab.4 Comparison table of simulation data

在加入阶跃响应后，传统算法在1 s后达到稳定状态并保持，而本文采用的自适应模糊PID算法只需要0.65 s就能够保持稳定。其次，算法在响应过程中的最大超调量，前者达到了8.5%，而后者则大幅降低为2%。

利用模糊PID算法对目标速度进行误差跟踪。爬壁机器人爬行过程中，通过不断改变左右电机的转速，进而改变爬壁机器人的运动方向，达到运动路径控制的目的。为了验证模糊PID算法对变化的输入信号的跟踪响应效果，本文通过编程给定一个变化的输入信号(0→1→0.2→0.5→1→0.4)，设定相应的参数值。输入变化的响应曲线如图7所示。通过响应过程得出，模糊PID控制器相比于传统PID控制器对动态变化的输入信号的跟随性较好，超调量较低，达到稳态的时间较快，具有较好的自适应性。

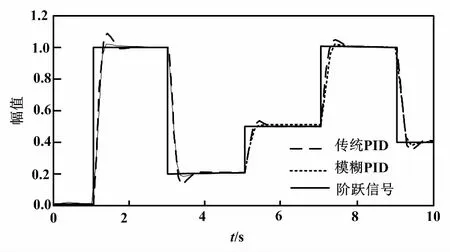
图7 输入变化的响应曲线Fig.7 Response curve of input change

5 结论

本文针对爬壁机器人爬行检测过程中出现的位姿偏差问题，提出一种基于自适应模糊PID算法的运动路径控制方法。该算法可根据实际情况在线调整PID的参数值，实现爬壁机器人的双闭环模糊控制。通过Simulink模块仿真分析，自适应模糊PID控制效果明显优于普通PID控制，对输入信号的跟随性较好，达到稳态的时间较快，超调量较低，控制效果显著提高。本文提出的双闭环运动路径控制方法能够快速、准确地控制爬壁机器人左右电机的转速，不断纠正其位姿偏差进而控制运动方向，使爬壁机器人沿目标轨迹稳定爬行。