三种典型炸药晶体微塑性与撞击感度的相关性

温茂萍，付 涛，唐明峰，谭凯元，徐 容，陈天娜

（中国工程物理研究院化工材料研究所，四川 绵阳 621999）

1 引言

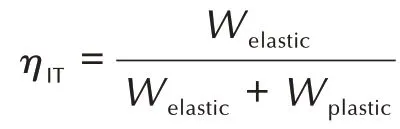
为了研究验证该观点，本研究采用纳米压痕仪表征晶体的弹性和塑性，压痕面内形貌和深度都是百纳米级，这种尺寸级别表征方法有别于宏观拉伸或压缩表征方法，两种方法表征的结果也可能会有差异，笔者认为用“微弹性”、“微塑性”定义由纳米压痕技术表征的微观弹性和微观塑性可能更明确。本研究提出以塑性压痕比（塑性能量与压痕总能量之比，ηP）量化炸药晶体微塑性的计算方法，将炸药晶体微塑性与其撞击感度建立起线性关系，为评价炸药安全等级提供一种研究思路。

2 实验方法与原理

2.1 炸药单晶

本研究按照文献［4，8-9］溶剂蒸发方法制备了炸药单晶。选取适量TNT、RDX、HMX 等炸药晶体，加入丙酮，搅拌状态下加热至一定高温，使其充分溶解，冷却至常温后过滤，将滤液放在一定温度的恒温箱中进行单晶培养，数十天后，得到毫米级TNT、RDX 和HMX 炸药大单晶作为实验样品。

2.2 炸药晶体结构的表征

利用Bruker 公司的D8 Advance X 射线衍射仪，对所制备的TNT、RDX、HMX 单晶进行XRD 测试，确定其晶型结构与最大显露晶面的晶面指数。测试中采用CuKα射线，X 光管操作条件为40 kV、40 mA，采用Vantec⁃1 一维阵列探测器，样品扫描范围为10°～60°（2θ）。利用德国耐驰公司STA449C 热分析仪测试了TNT 单晶的DSC 曲线，升温速率为10 ℃·min-1。

2.3 炸药晶体的微弹性与微塑性表征方法

利用Hysitron 公司Triboindenter 纳米压痕仪测试了TNT、RDX、HMX 三种炸药大单晶微观压力性能。测试中选取Berkovich 金刚石压针，采用“加载⁃恒载⁃卸载”与时间线性的控制方式，加载、恒载和卸载的时 间 分 别 为10，5，10 s，恒 载 力 分 别 为500，1000，2000，、3000，4000，6000 μN 和9000 μN，将这7 个恒载定义为峰值载荷。加载测试完成后，采用压痕仪的Triboindenter 原位成像功能，对500 μN 和9000 μN 两种恒载条件的三种晶体进行了残余压痕形貌成像。

纳米压痕测试能够获得如图1 所示的典型“载荷⁃深度”曲线，根据图1 由Oliver⁃Pharr 原理可以计算材料微观力学性能参数［12］。最常用的计算参数为压入模量（EIT），其数值与材料杨氏模量最接近，可用于表征材料弹性特性，其计算方法如公式（1）：

式中，νS为试样的泊松比，一般取0.25［14］，Ei、νi分别为金刚石压针的弹性模量和泊松比，其值分别为1140 GPa 和0.07［14］。Er为 压 入 折 合 模 量，GPa，计 算公式见式（2）：

图1 典型的“载荷⁃压入深度”曲线示意图Fig.1 Typical schematic relation of loading⁃indentation depth

式中，S 为接触刚度，N·m-1，通过图1 中的卸载曲线起始段斜率计算获得，β 是与压头形状有关的常数，对于三角形Berkovich 压头取为1.034［15］，Ac为压头和试样接触的投影面积，μm2，可根据压入深度以及压头形状计算。

由于纳米压痕的晶体塑性量化表征方法还没有建立科学统一的标准，所以采用与压痕深度相关的无量纲 参 数 定 量 表 征 法，用 无 量 纲δh表 示［17］，计 算 公 式见式（3）。

式中，hmax、he、hp分别为最大压入深度、弹性回复深度、残余压痕深度，单位：nm。

本文参考公式（3）的压痕深度比方法［17］，提出一种与能量相关的无量纲参数量化炸药晶体的微塑性，用无量纲ηP表示，计算公式见式（4）：

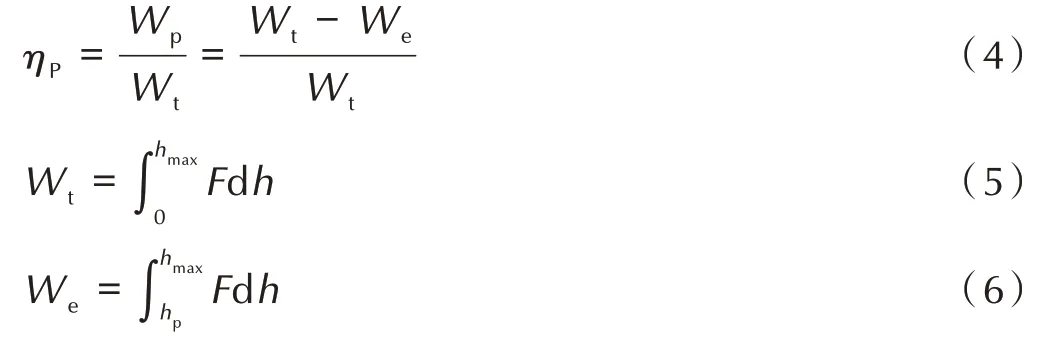
式中，Wp为压入塑性能量，Wt为压入总能量，We为压入弹性能，f J。

3 结果与讨论

3.1 三种炸药单晶结构

三种炸药大单晶照片如图2 所示，其中TNT 单晶呈现淡黄色，宽度及厚度均达到数毫米以上，长度方向已达到了厘米级，在尺寸上已能满足纳米压痕仪的测试要求。RDX 和HMX 两种单晶均呈现出无色透明，虽然形状不如TNT 那样规则，但尺寸同样也达到数毫米，可以用于压痕测试。

图2 三种炸药单晶形貌Fig.2 Single⁃crystal appearances of TNT，RDX and HMX explosives

图3 三种炸药单晶的XRD 曲线Fig.3 XRD curves of TNT，RDX and HMX single⁃crystal

TNT 存在单斜和正交两种晶型结构，其中单斜为稳定的常用晶型。RDX 有Ⅰ、Ⅱ两种晶型结构，其中Ⅰ⁃RDX 单晶为正交晶型，Ⅱ⁃RDX 极不稳定。HMX 存在α、β、γ、δ 等四种晶型结构，其中β⁃HMX 为单斜晶型［18］。图3 是所制备的TNT、RDX 和HMX 三种单晶最大显露晶面的XRD 曲线，与剑桥结构数据库（CSD）的晶体结构比对，发现它们均为实际使用较多的、最稳定的晶型结构：TNT 近似为单斜晶型（晶胞参数：a=21.275 Å，b=6.093 Å，c=15.025Å，β=110.14°），RDX 为正交晶型，最大显露晶面为（210）晶面（晶胞参数：a=13.202 Å，b=11.601 Å，c=10.717），HMX 为单斜晶型，最大显露晶面为（011）晶面（晶胞参数：a=6.537 Å，b=11.054 Å，c=8.7018 Å，β=102.8°）。为了进一步证明制备的TNT 试样为单斜晶型，对TNT 大单晶进行了DSC 分析，结果如图4 所示。由图4 可见，TNT 大单晶只存在一个81.07 ℃熔融峰，而正交TNT晶体除了82 ℃熔融峰外，还存在一个72 ℃较小熔融峰［4，15］，从而确定所制备TNT 单晶确实为单斜晶型。

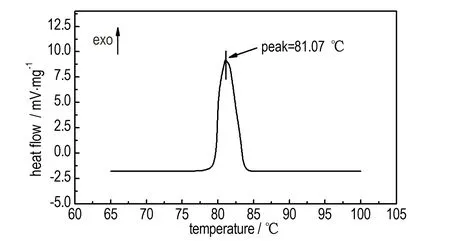
图4 TNT 单晶的DSC 曲线Fig.4 DSC curvet of TNT single⁃crystal

3.2 三种炸药晶体的纳米压痕测试曲线

分别在所制备的单斜晶型TNT 单晶（100）晶面、正交晶型RDX 单晶（210）晶面和单斜晶型HMX 单晶（011）晶面上，进行了500，1000，2000，3000，4000，6000 μN 和9000 μN 7 个不同恒载程度的压痕试验，测试曲线见图5。由图5 可见，三种炸药晶体压入深度随压入载荷的变化过程相似，当压入载荷较小时，压入深度变化较大；当压入载荷较大时，压入深度变化较小，其载荷值拐点均在2000 μN 附近。

图5 三种炸药单晶的纳米压痕测试曲线Fig. 5 Typical nano⁃indentation test curves of TNT，RDX and HMX single⁃crystal

3.3 三种炸药晶体的微弹性

根据三种炸药单晶的纳米压痕测试曲线（图5），采用公式（1）计算了三种炸药单晶在不同峰值载荷下的压入模量EIT，得到图6。从图6 可以看出，在所有峰值载荷最低时，基于纳米压痕曲线计算获得的三种炸药晶体压入模量最小，详细值见表1 中Emin，与其他文献［11，14-15］测试值相当。随着压入峰值恒载的提高，压入模量略有增加，7 个压入峰值载荷计算后的平均压入模量（-E）见表1。由于纳米压痕压头与试样表面接触时，试样压痕上应力分布较为复杂，还需结合炸药晶体在不同峰值恒载下的压痕弹塑性区域分布的变化及其对压入模量计算结果影响分析，才能充分解释三种炸药晶体压入模量随压入峰值载荷的变化趋势。

图6 不同恒载条件下三种炸药晶体的压入模量Fig.6 The indentation modulus of TNT，RDX and HMX crys⁃tals under different holding loads

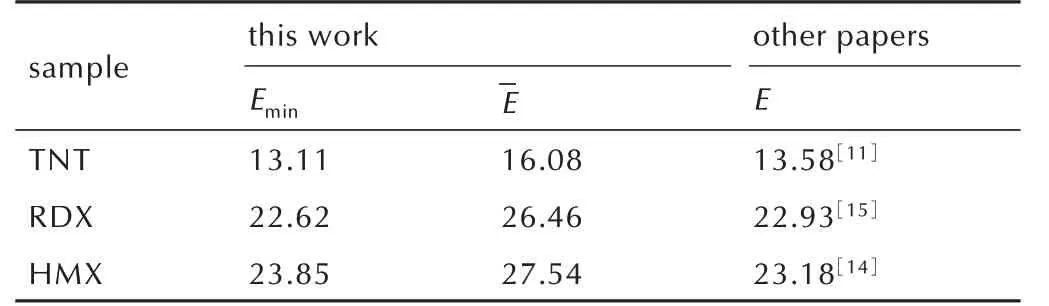
表1 TNT、RDX、HMX 单晶的压入模量Table 1 Single⁃crystal indentation modulus of TNT，RDX and HMX from different researches GPa

3.4 三种炸药晶体的微塑性

材料塑性最为直接的表现是材料在所施加载荷卸载后会残留不可恢复的变形，三种炸药单晶在经过500 μN 压载后的残余压痕形貌如图7 所示。但仅从残留的压痕形貌量化材料的塑性还不够严谨，因此一般采用公式（3）提及的压痕深度比δh来量化材料的微塑性。

采用Hysitron 公司Triboindenter 纳米压痕仪测量的最大压入深度和残余压痕深度如图8 所示。

结合图6 炸药晶体的压入模量，从图8a 可以看出，压入弹性模量小的TNT 单晶，最大压痕深度在相同的峰值载荷下均为最深，而RDX 与HMX 的压入弹性模量相近，两者最大压痕深度也相近。从图8b 可以看出，在500～9000 μN 峰值载荷范围内的压痕加载后，三种炸药晶体表面均会产生残余压痕。当峰值载荷较小时，三种炸药晶体残余压痕深度差异相对较大，可以认为是三者晶体的塑性不同；随着恒载压力增加，残余压痕差异减小，在峰值载荷为9000 μN 时，三种炸药晶体的残余深度几乎相等，其残余压痕形貌如图9所示。

图7 恒载为500 μN 时三种炸药晶体的残余压痕形貌Fig.7 Residual indentation patterns of TNT，RDX and HMX crystals after 500 μN holding loads

图8 三种炸药晶体最大压痕深度、残余压痕深度随峰值载荷变化曲线Fig.8 Relationships of maximum and residual indentation depths and corresponding peak loads for TNT，RDX and HMX crystals

利用公式（3）计算出三种炸药单晶的微塑性δh与最大恒载力有关，如图10 所示。由图10 可以看出，在压入峰值载荷不大于2000 μN 时，三种炸药晶体微塑性参数δh值差异较小，在压入峰值载荷大于2000 μN后，RDX 和HMX 的微塑性δh差异较小，TNT 的微塑性δh值小于前两者。

但是，笔者认为也可以从能量相关角度来量化炸药晶体的微塑性，以ηP表征，按照公式（4）计算出500～9000 μN 压痕载荷范围内的ηP，结果如图11 所示。由图11 可见，ηP与δh类似，呈下降趋势。由于采用的计算方法不同，三种炸药晶体的塑性特征参量的排序有所不同，在2000 μN 恒载以上，规律比较明显，以δh表征时，三者的微塑性排序为TNT＜HMX＜RDX，以ηP表征时，微塑性排序为TNT＜RDX＜HMX。两种表征量化方式都有一定的科学依据，但ηP不仅包含深度因素，还包含力的因素，整体表现出做功（或称为机械能）。在机械载荷作用下，机械能量的一部分储存为晶体可恢复变形的弹性能量，另一部分造成了晶体出现不可恢复的塑性形变。因此，用与能量相关的ηP表征的微塑性与炸药晶体的机械感度更紧密关联。

目前尚未有毫米级炸药晶体的机械感度数据，但在董海山［19］先生论著中有对微细晶体单质炸药的落锤撞击感度的测试方法和数据：TNT 为4%，RDX 为80%，HMX 为95%。将本研究测试获得的δh、ηP与三种单质炸药落锤撞击感度P 进行了相关性分析，结果见图12。由图12 可见，δh与P 相关性不强，而ηP与P的线性相关度高达95.8%。分析认为，δh表征的晶体微塑性只包含变形部分，而ηP中不仅包含变形，还含有与能量相关的载荷和压入位移，所以以可量化的微观力学性能分析与能量相关的感度具有合理性。另外，炸药在撞击作用下发生爆炸反应，本质上是撞击能量转换的结果。这一结果再次支撑了“以能量相关量化的炸药晶体微塑性与炸药撞击感度具有高度线性相关”的结论是比较合理的。

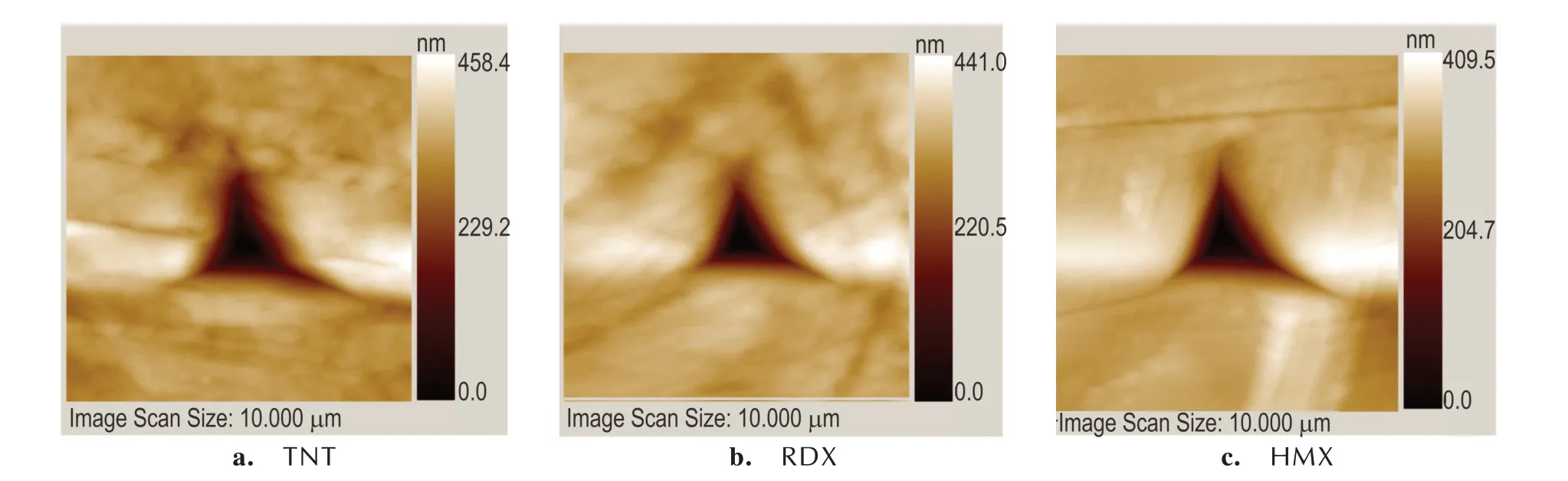
图9 恒载为9000μN 时三种炸药晶体的残余压痕形貌图Fig.9 The residual indentation patterns of TNT，RDX and HMX crystals after 9000μN holding load

图10 三种炸药晶体的δh⁃Fmax关系Fig.10 Relationship of δ h⁃Fmax ofTNT，RDX and HMX crystals

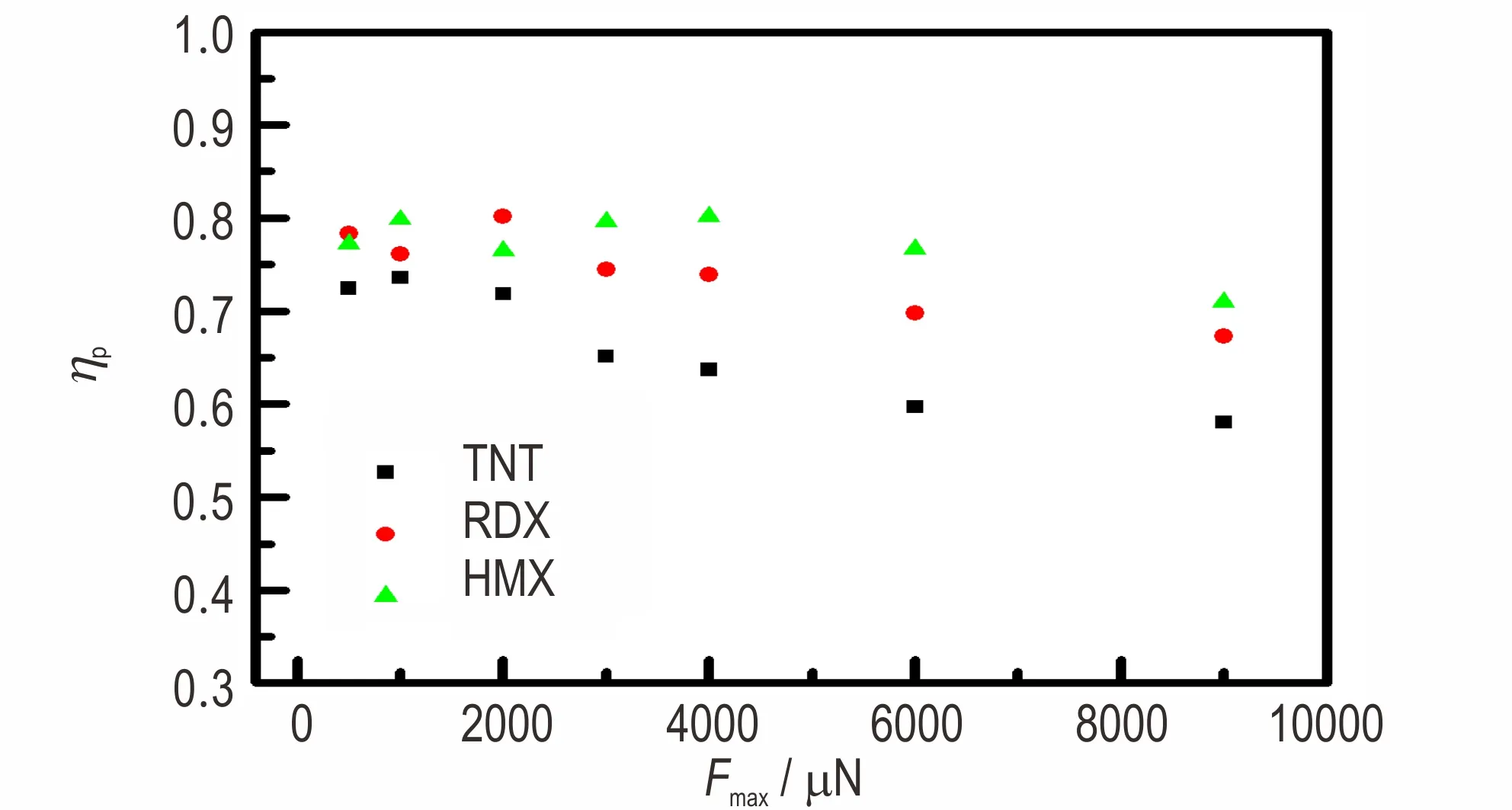
图11 三种炸药晶体ηP⁃Fmax关系Fig.11 Relationship of ηP⁃Fmax of TNT，RDX and HMX crystals

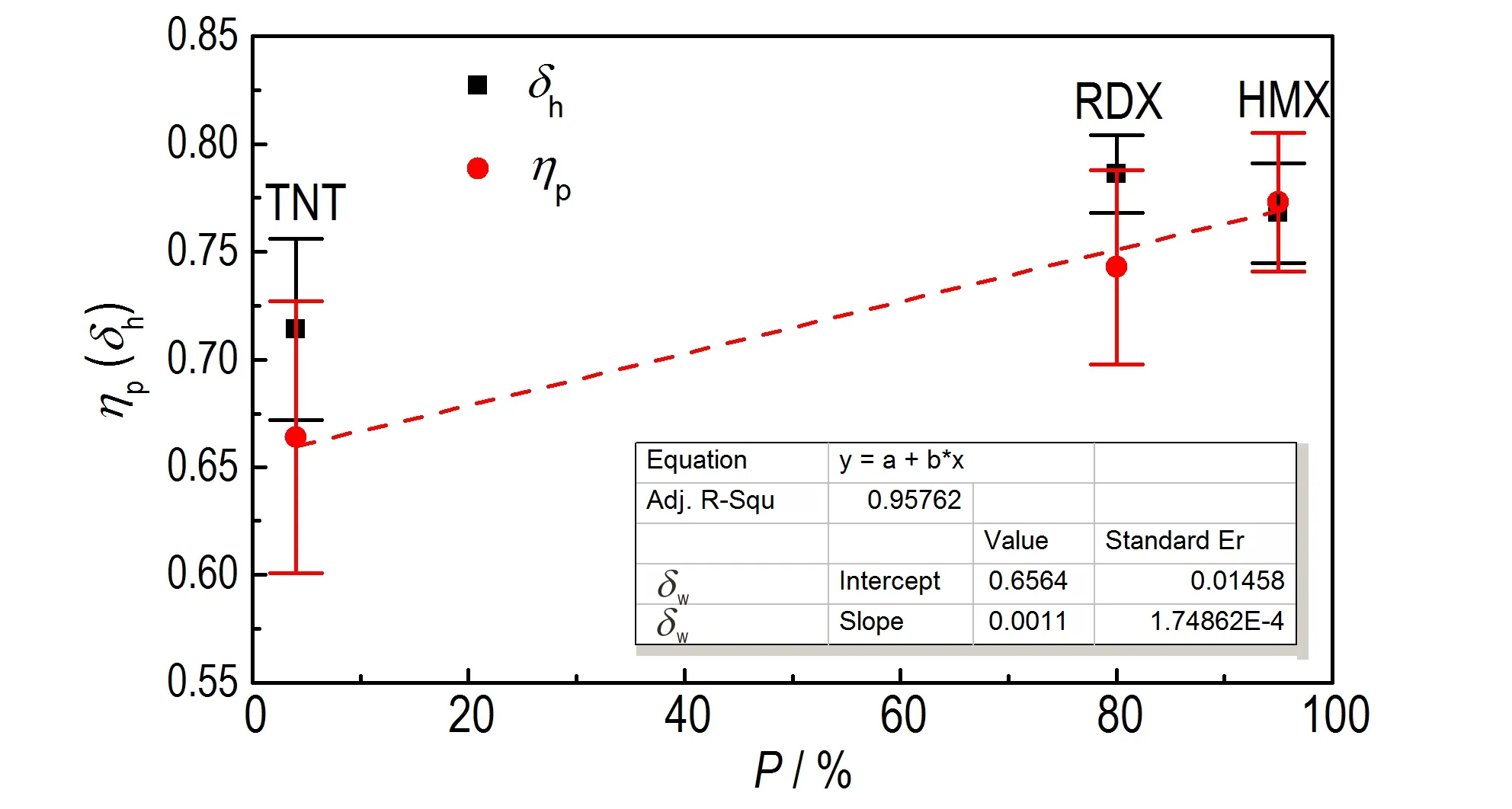
图12 炸药晶体微塑性与其粉末态撞击感度的关系Fig.12 Relationships between micro⁃plastic performance of TNT，RDX and HMX explosives crystals and their impact sen⁃sitivity in powders

4 结论

采用纳米压痕技术获得了TNT、RDX 和HMX 三种炸药晶体的“加载⁃恒载⁃卸载”测试曲线，提出了一种与炸药感度密切相关的微观塑性量化方法，结论如下：

（1）基于纳米压痕技术提出了一种以能量相关的炸药晶体微塑性量化方法，获得的TNT、RDX 和HMX三种常用炸药晶体微塑性ηP与压入深度计算获得的δh排序略有不同，从三者的撞击感度与它们的微塑性高度线性相关结果分析，认为所提出的微塑性量化方法更合理。

（2）此外，测试获得了TNT、RDX 和HMX 三种常用炸药的微弹性参数EIT，RDX 与HMX 的EIT比较接近，TNT 的EIT明显小于RDX 和HMX。