基于用电模式聚类的层级电力时序预测方法

沈泉江 郭乃网 郑作梁

1(上海市电力科学研究院 上海 200437) 2(星环科技(上海)有限公司 上海 200233)

0 引 言

电力需求预测是电网系统中的一个十分重要的问题，关乎国家的发展大计[1]。精确的电力需求预测可以有效地指导电力系统有关部门的合理决策和管理，从而促进国家经济发展，以及缓解生态环境问题。随着智能电网系统地快速发展，海量的用电数据不断地产生，其蕴含了极大的潜在价值[2]。由于电力数据的规模极大，种类繁杂，因此如何高效合理地利用这些数据是一个亟待解决的问题。

目前，常用的电力需求预测模型大多是基于地理层级结构的[3]。例如，一个城市的电力需求可以通过行政区划划分为若干区域，并再进一步划分为若干街道、街区。图1展示了6个不同城市的代表性的用户用电时间序列曲线。

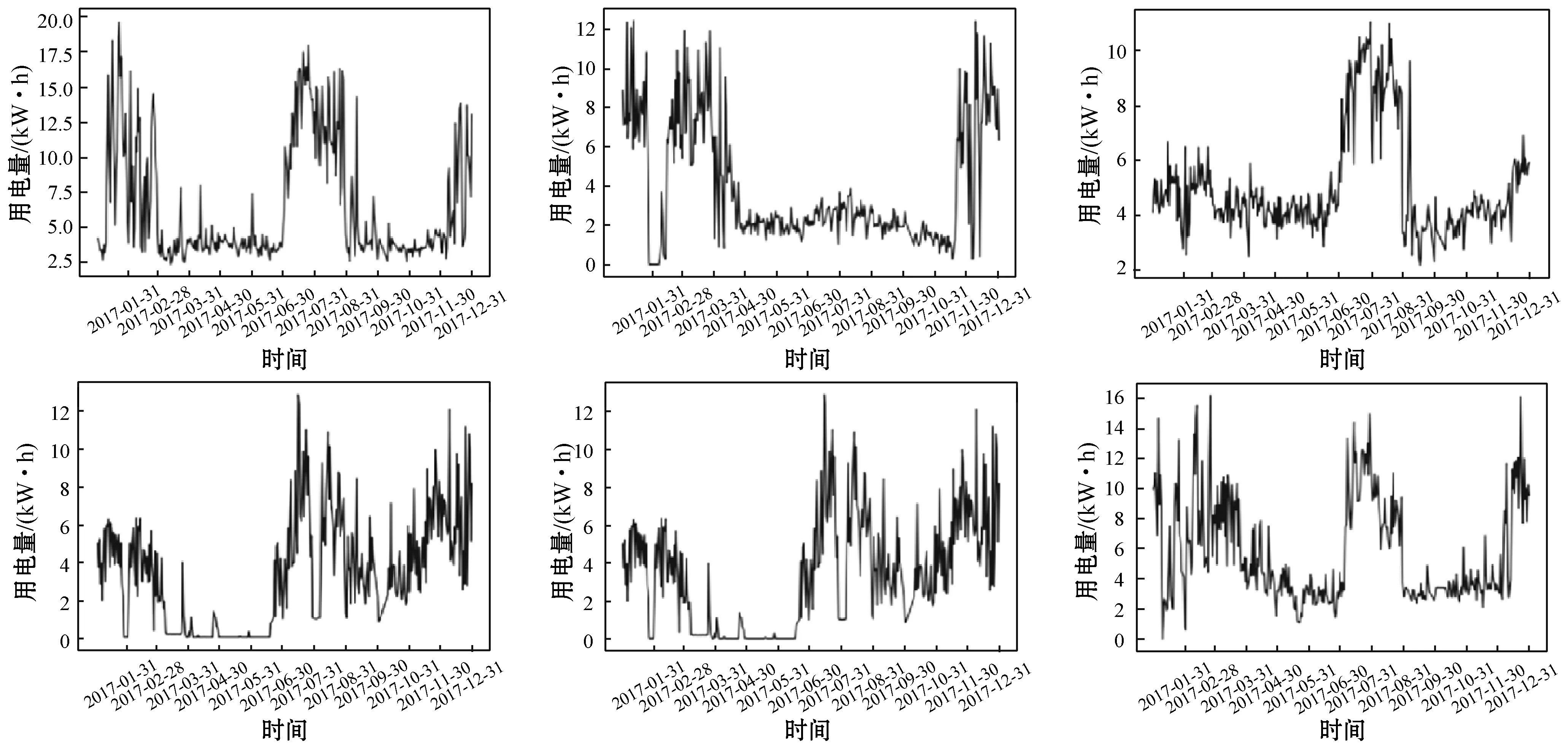
图1 不同地理区域的代表性用电时间序列曲线

本文提出一种基于用电模式聚类的层级电力时序预测方法。相对于传统的用电预测模型，该方法能够自动地对层级结构的用电数据进行建模，并且其预测精度显著提升。该方法的主要创新点如下：

1) 使用ST-DBSCAN聚类算法自动地对家庭用电数据进行聚类，从而构建用电模式的层级结构。2) 基于聚合一致性将层级预测建模为最优GLS回归问题，直接通过梯度下降法求解。3) 加入L1正则化降低模型的复杂性，防止模型训练陷入过拟合，从而提高模型的泛化能力，并使得MAPE和RMSE指标也得到显著提高。

1 层级电力时序预测基本原理

层级电力时序预测是智能电网中一个十分重要的课题，区别于传统的电力预测，其难点主要体现在如下两点：

1) 时序性。即对电力的预测不仅要考虑环境、电费、政府政策等外部特征因素，还需要考虑用户自身的历史用电曲线，根据历史曲线体现出的用电规律或者用电模式，来预测用户接下来用电曲线的变化。

2) 层级性。用户的用电量、用电习惯与用户的地理区域分布具有很强的相关性，例如北方用户的用电量大多集中在冬季(取暖用电)，而南方用户的用户量大多集中在夏季(防暑用电)。因此，不同地理区域的用户可以根据其所在街道、城乡、县市、省份等层次进行逐层归类与划分。因此，在层级预测中，我们很关心同一层级的用户之间、父子层级的用户之间的用电模式是否存在一些隐含的关系，这种隐含关系能够辅助我们更好地预测用电模式。此外，相较于直接对电力时序数据进行预测，层级预测具有更加良好的可解释性，并且能够在一定程度上降低模型的计算量。

聚合一致性是层级预测中的关键，即分解后的若干时间序列的加和应当同高层次聚合后的时间序列相等。由于在整个时间序列的独立预测中很难保证聚合一致性，因此目前在工业界中往往采用“自底向上”的方法。然而，当分解后的数据信噪比较低时，现有的方法往往预测精度较差[4]。近年来，各种基于最优调节的方法逐渐成为了主流，例如Hyndman等[5]提出了一种基于最小二乘协调法处理层级预测问题的方法。然而，由于调节的副作用可能会扩大预测误差，因此通常以牺牲预测精度为代价来实现聚合一致性。

为了避免聚合一致性带来的预测精度降低，本文提出了一种全新的电力需求层级预测方法。该方法不直接对地理层次结构进行处理，而是对用电模式检测进行时间序列的聚类分析。由于个人家庭用电往往在一定程度上随时间稳定增长，因此本文基于聚类结果，构建了一个新的基于用电模式的时间序列层级结构。通过将具有相似模式的时间序列组合在一起，可以显著提高聚合时间序列的信噪比，从而提高聚合时间序列的预测精度。在此基础之上提出了一种新的优化调节方法，以提高分解时间序列的预测能力。最后采用“自底向上”的方法对分解后的预测结果进行汇总，形成各种高层级的聚合预测，从而实现了地理层级结构的聚合一致性。

2 算法设计

2.1 用电模式分析

首先探讨一下智能电表数据的用电模式。用电模式是利用ST-DBSCAN[6]聚类算法从个体家庭时间序列的数量中提取出来的。ST-DBSCAN聚类算法是一种基于DBSCAN算法的改进，本质上也是一种基于密度的聚类算法。ST-DBSCAN拥有传统的DBSCAN具有的优势：基于密度的聚类，即给定密度阈值，如果两个点的距离小于这个阈值，那么将其划分至同一个类别。相较于K-means算法，ST-DBSCAN不需要提前定义好类别数K，其能够自动地学习出最适合的类别数。此外，ST-DBSCAN相较于DBSCAN，其在时空数据上的表现更加优异，与用电时序数据的地理区域分布和时序特征恰好吻合。

以图2为例，其展示了将5个时间序列进行聚类，并抽取出其用电模式的过程。首先对于这5个用电时间序列，采用ST-DBSCAN将其划分为两个类别，然后通过时间序列的聚合算法，将每个聚类中时间序列的共性提取出来，从而得到能显著代表聚类中所有时间序列的整体趋势共性的用电模式。

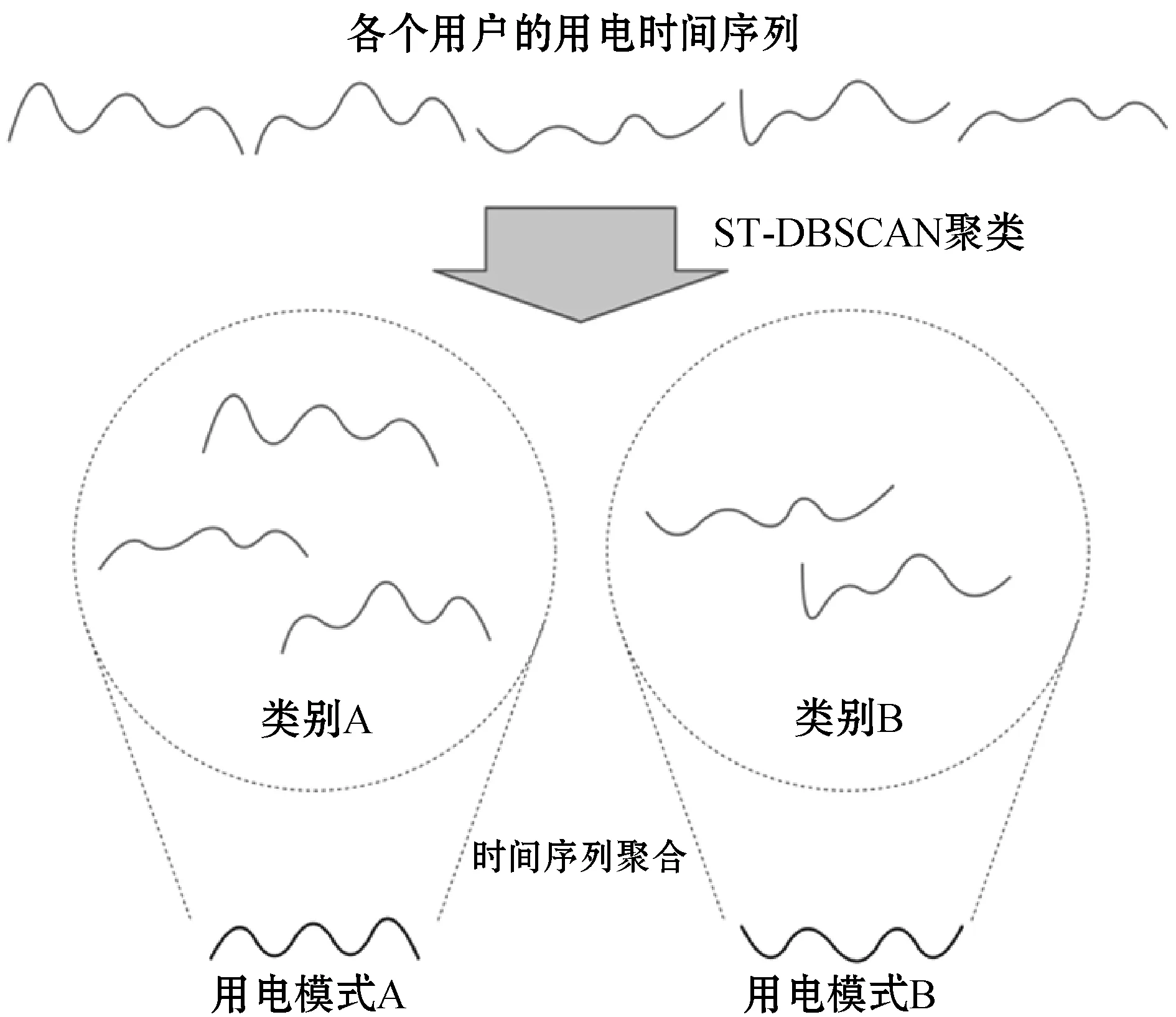
图2 基于ST-DBSCAN聚类的用电模式分析过程

2.2 层级结构构建

不同层级的用电消费水平大体上是一致的。如果聚合时间序列的预测是准确的，那么在聚合约束和调节的情况下，单个时间序列的平均预测精度就有可能得到提升。此外，用电时间序列的模式要比基于地理层级结构的聚合时间序列更为规则。因此，基于用电模式的预测误差应当要小于基于地理区域聚合时间序列的预测误差。

基于这个想法，本文构建了一个基于用电模式的层级结构，如图3所示。这种层级结构由高层的用电模式和低层的单独的时间序列构成。最左列的用电模式向右衍生出三个子用电模式，如中间列所示。这三个用电模式又分别向右衍生出它们各自的用电模式。可以看出，属于同一个父节点的用电时间序列曲线，其用电的变化规律十分相似，只是在变化幅度上有略微的差异。

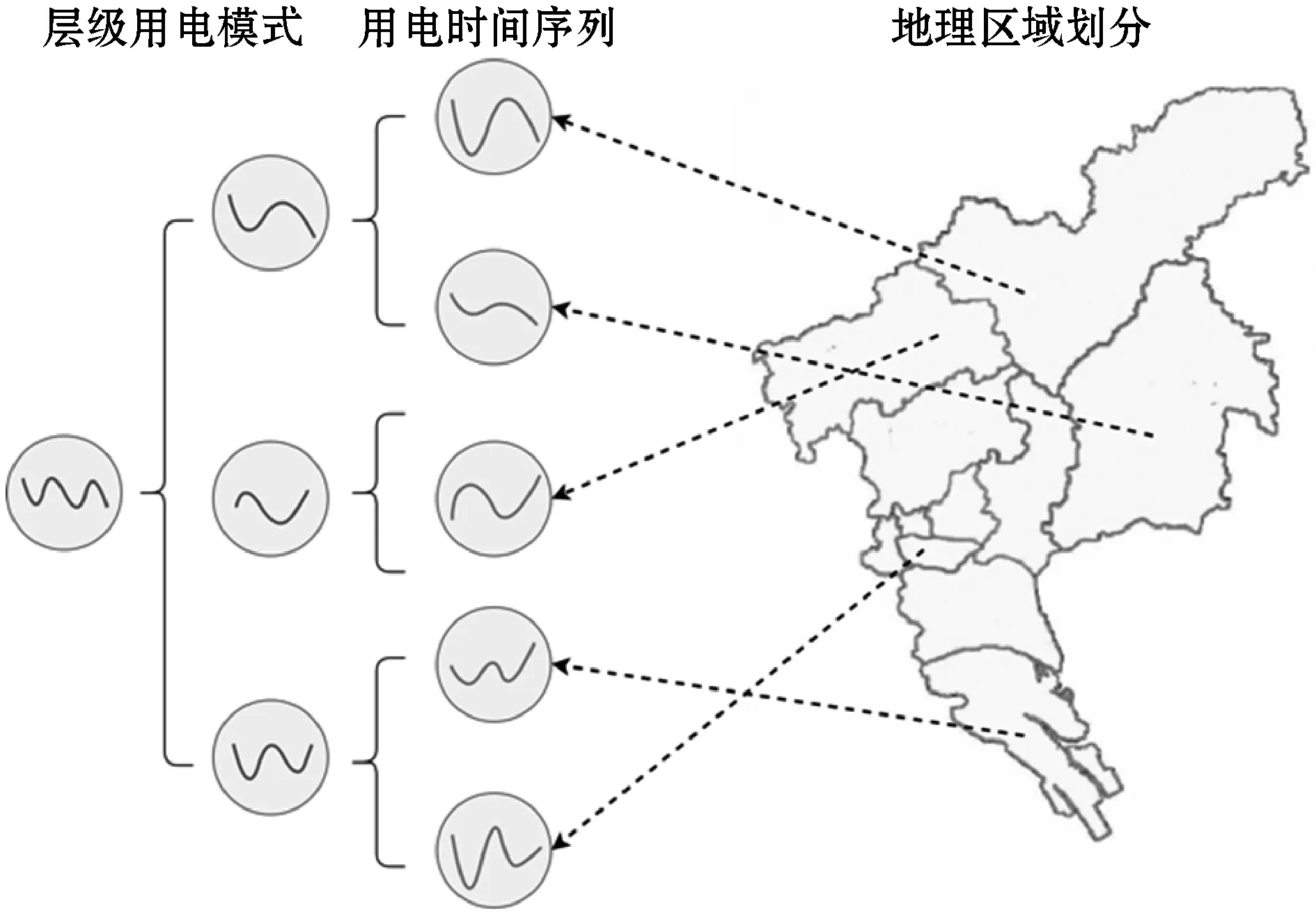
图3 基于用电模式聚类的层级结构

这种层级结构相较于传统的用电预测方法，其优势主要体现在它充分利用了地理区域相近的用户具有相似的用电模式这一先验特征。并且在理想情况下，层级结构的深度是Log级别的，其运算复杂度很小。此外，层级结构中的每一层有对应的具体含义，例如顶层代表国家、底层代表街道，这样，模型的预测结果就具有更好的可解释性。

2.3 基于聚合一致性的层级预测

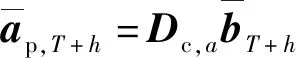
(1)

本文目标是通过最小化平方预测误差的期望值来获得调节后的底层预测：

(2)

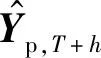
式(2)中的最优解可以通过最佳线性无偏调节预测得到：

(3)

式中：Uh表示h时间段内的预测误差的协方差矩阵。

根据广义最小二乘法(GLS)[8]，式(3)中的底层预测结果也可以通过回归模型来得到：

(4)

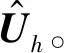
(5)

通过这种方式，将问题建模为一个关于预测误差的最优GLS回归问题，可以使用梯度下降法[9]求解。

为了使得优化更加快速且鲁棒，本文使用了Adam算法[10]取代传统的随机梯度下降优化算法(Stochastic Gradient Descent)进行优化。相对于传统的随机梯度下降法，Adam算法的优势主要体现在如下两个方面：1) Adam算法引入了动量(Momentum)机制，通过指数加权平均(Exponentially Weighted Averages)方法，在每次对一个Batch的数据做梯度下降时，通过一个超参数来控制每次的梯度一部分来自最新计算的值，另一部分来自历史保留的值，从而使得最终得到的梯度为过去几个Batch的平均值。历史Batch梯度的平均值等效为动量，可以加速网络向过去累积更新量最大的方向进行更新，显著地加快模型的收敛速度。2) Adam算法引入了RMSprop机制，在每个Batch计算梯度时，也利用了指数平均加权方法，对梯度的平方根倒数进行累加平均。达到的效果是：每个Batch计算出的梯度能够根据历史梯度的震荡情况，自动消解来回震荡幅度大的方法，避免梯度在无意义的方向上来回摆动，从而加速收敛并增加了训练的鲁棒性。

此外，我们在训练的过程中也引入了一些其他防止模型过拟合的机制，例如L1正则化、BatchNorm、Dropout等。BatchNorm即在Adam算法每次取一个Batch的数据时，将数据在一个Batch内进行归一化，使得特征的均值为0，并且起到了一定的数据增强作用(每个样本在不同的Batch中的特征值均不同)。Dropout则是在每个Batch训练的过程中，随机地丢弃若干输入数据的特征，通过加入一定噪声增加模型的鲁棒性。本文将Dropout的概率设为0.5。

2.4 L1正则化

正则化属于结构风险最小化策略，能够有效地防止参数过大所导致的过拟合。L1正则化是一种常见的正则化技术，也称为L1范数，其等于模型权重的绝对值之和。L1正则化具有以下特点：

1) L1正则化可以防止模型的权重过大，起到防止过拟合的作用(但其正则化强度略低于L2正则化)。

2) L1正则化可以使模型得到一组相对稀疏的权值，也就是当模型收敛后，权值矩阵中有很多值接近0。

因此，我们在式(5)所示的优化目标中加入了L1正则项[11]：

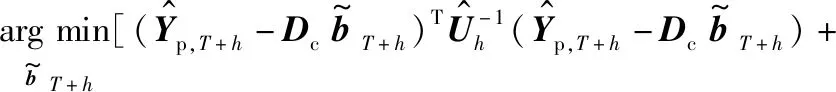
(6)

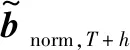
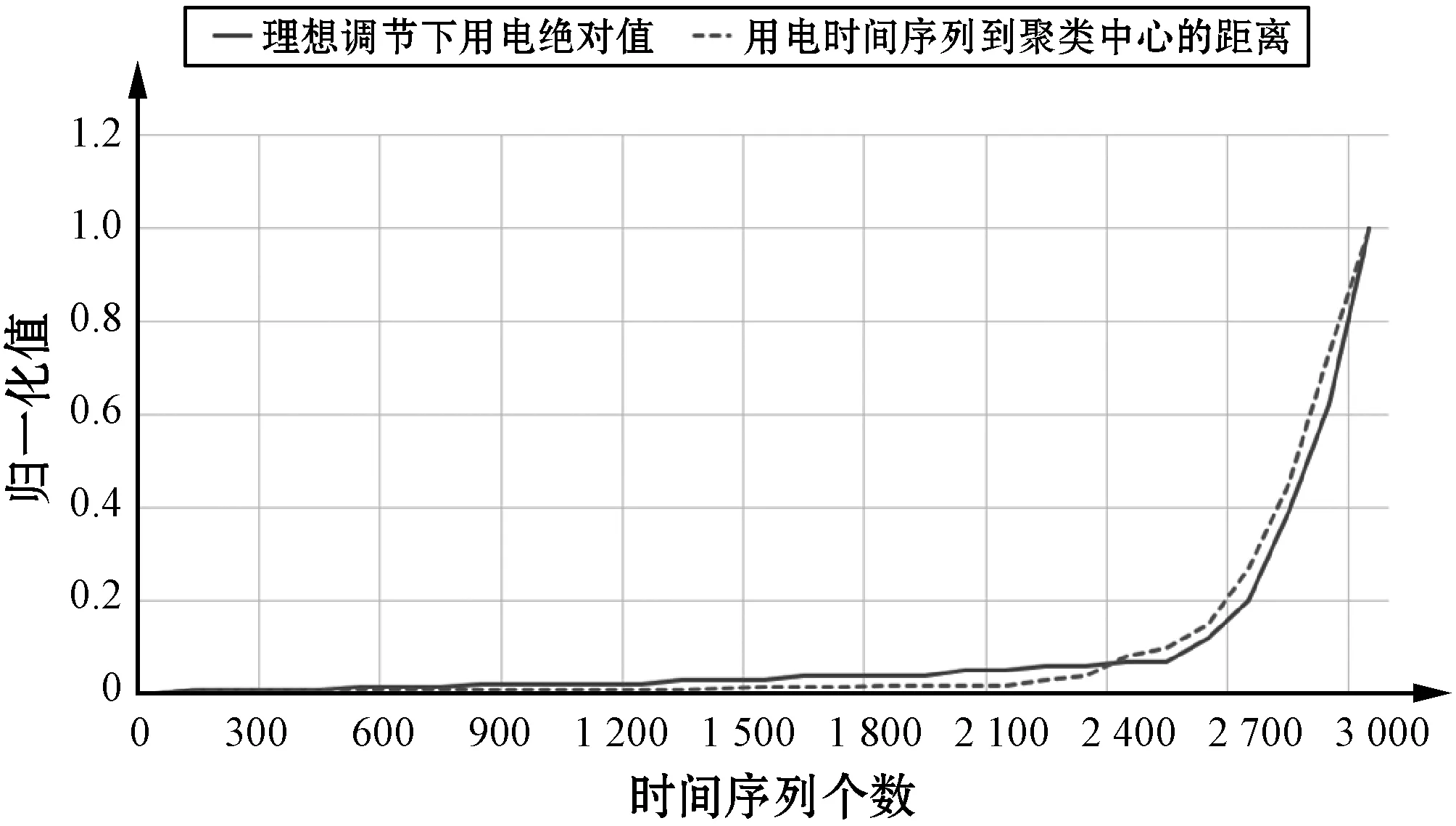
图4 理想调节下用电绝对值与用电时间序列到聚类中心距离的分布对比

用电时间序列与其用电模式越相似，也就意味着这个用电时间序列是越稳定和正规的，即当时间序列越接近聚类中心时，其预测结果越准确，因此需要的调整也就越小。为了确定如何达到最优的调节，本文引入了正则化项来惩罚序列调整分布与其对应模式隶属度的相关性。当用电时间序列接近聚类中心时，通过求解式(6)得到的相应的调整值将较小。

3 实 验

3.1 实验数据与设置

在本文实验部分，采用了来自能源需求研究项目的公开电力数据集：EDRP(Early Smart Meter Trials)[12]。该数据集是关于个人家庭用电消耗的真实数据集，包含了2 501个时间序列，时间序列的采样间隔为30分钟。

在实验中，利用数据集上的历史消耗观测值，来计算提前一步滚动预测[13]。对于EDRP数据集，重复了48个预测任务，从2009年5月9日至2009年5月20日，预测全天的电力需求。此外，使用平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)和均方根误差(Root Mean Square Error，RMSE)来测量预测误差，它们分别表示家庭用电量的相对预测误差和平均预测误差。

在对比实验中，将本文方法与目前常用的模型进行比较，其中包括BASE、WLS[14]和MinT-Reg[15]。同时，也对加或不加L1正则化项的本文方法分别进行了实验，L1正则化参数λ的取值为104。

3.2 实验结果分析

在EDRP数据集上的每个层级的预测精度和平均统计结果分别如表1和表2所示。

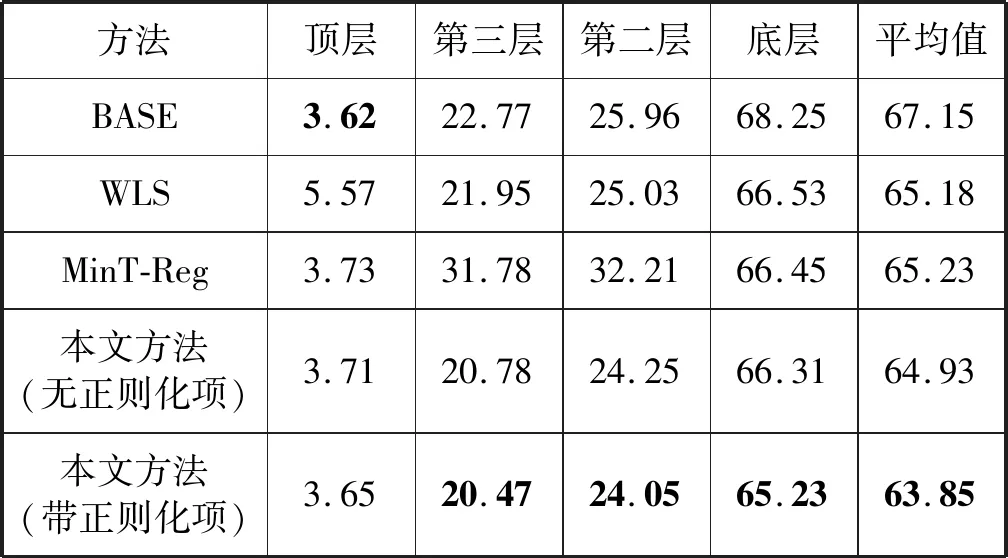
表1 不同方法的MAPE比较

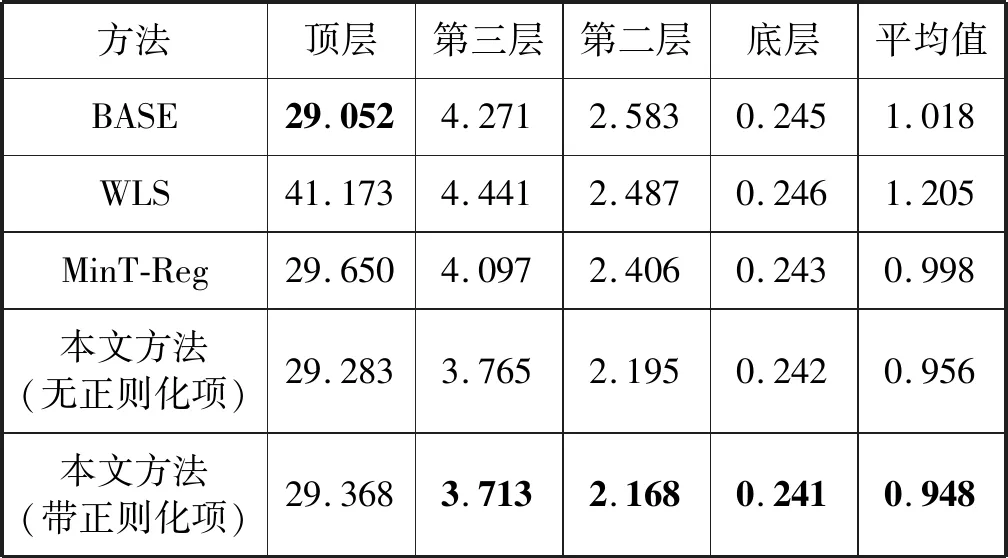
表2 不同方法的RMSE比较

可以得出，高层的预测结果的误差往往比低层的预测误差更小。这是因为高层的预测由于聚合而具有更高的信噪比。也可以观察到，BASE模型在一些高的层次的预测误差最小，但是其不能够保证地理聚合的约束。相比之下，在大多数情况下，本文方法不仅满足了地理聚合的约束条件，而且实现了比BASE模型更高的预测精度。

此外，在EDRP数据集上带正则化项的本文方法取得了最高的预测精度，并且带L1正则化项的方法比不带L1正则化项的方法展示出了更明显的优势。这是因为L1正则化项遵循结构风险最小化准则，防止模型陷入过拟合从而影响精度。总的来说，就MAPE和RMSE这两个指标而言，带L1正则化项的本文模型在公开的真实场景数据集上比对比模型具有更好的预测能力以及更强的鲁棒性。

4 结 语

聚合一致性是层级时间序列预测的关键点之一。在以往的大多数工作中，预测过程通常受到地理聚集约束的影响，从而造成预测精度的损失。在本文的工作中，证明了灵活使用聚集约束可以带来用电需求预测的改进。为了解决预测精度损失的问题，本文通过用电模式分析建立了一个新的数据层级结构。然后基于新的层级结构，提出了L1正则化回归方法，并使用Adam算法进行快速训练，在现实的用电场景中，显著地提高了聚合和分解时间序列的预测精度。未来将在电力需求预测及其相关的其他应用领域，探索新的层次构建方法和具有聚合一致性的优化预测方法。