基于三向Dexel的GPU加速数控仿真方法

李一鹏 贾世宇 潘振宽 王吉强 李 冰

(青岛大学计算机科学技术学院 山东 青岛 266000)

0 引 言

数控仿真对数控加工有着重要的意义。数控仿真通过在虚拟环境中使用数控加工程序模拟加工过程来验证其正确性，避免因数控加工程序错误而导致的工件质量下降和资源浪费。

现代数控仿真一般使用基于空间分割的方法来表示工件模型实体，其中由Hook[1]提出的Dexel方法广泛地应用于国内外商业软件和仿真系统中。基于Dexel的仿真方法的主要问题在于表示几乎平行于Dexel方向的部分实体时精度较差，存在难以避免的阶梯化现象与信息丢失的问题。其改进版本三向Dexel方法则可以在保留其简单布尔操作以及较小空间占用优点的同时增加建模的精度。三向Dexel方法在数控仿真中应用的主要问题在于复杂的表面重构过程。目前主流的做法是利用三向Dexel模型与体素(Voxel)模型的相似性，将三向Dexel模型转换成体素模型，再使用成熟的体素模型表面重构算法进行表面重构[2]。于珊[3]通过使用GPU加速的移动立方体(Marching Cube)[4-5]方法进行表面重构提高了数控仿真的速度。Peng等[6]提出的基于轮廓的表面重构方法及Ren等[7]提出的基于网格的表面重构方法相比于将三向Dexel模型转换为体素模型，其算法复杂度较高，时间消耗较大，且难以使用并行技术进行加速。Jachym等[8]通过使用OptiX光线追踪引擎来获取更具真实感的重构表面，但难以实现流畅的实时仿真。Inui等[9]提出的四面柱(Quad Pillars)算法拥有较高的并行度和执行效率，但是仅适用于单向Dexel模型的表面重构。

相比于移动立方体方法，双轮廓(Dual Contouring，DC)[10]方法通过使用厄米特数据(Hermite data,物体表面点及其法线数据)计算特征点，可以还原由于采样问题丢失的特征(如尖锐棱角特征)。双轮廓法在数控仿真中应用的主要限制在于其高昂的计算开销，在CPU端进行的双轮廓法往往难以满足数控仿真对于实时性的要求，因此目前该方法还未在数控仿真中有所应用。

针对上述问题，本文提出一种并行化的基于三向Dexel的数控仿真方法，通过使用三向Dexel建模方法提高仿真精度，采用双轮廓方法进行表面重构，并通过运用并行加速技术提高计算速度。相较于现存的数控仿真方法，在仿真的精度相同时，本文方法使用的GPU加速的双轮廓算法能够更准确地还原出数控加工工件的尖锐棱、角特征，为实际加工提供更加准确的仿真结果。同时通过应用多线程加速和GPU加速技术，使得中等配置(参考配置见仿真结果部分)的计算机也能实现流畅、准确的仿真，降低了对计算机硬件的要求。

1 仿真方法

数控仿真方法的结构如图1所示。数控仿真程序在CPU端、GPU端有不同的分工。仿真程序从存储工程文件中读取信息后，在CPU端根据胚料信息进行实体建模，根据刀具参数计算每行NC代码控制下刀具所扫过的空间体(下简称为扫掠体)；将工件实体与扫掠体进行相减操作；将所得三向Dexel模型转换成适合进行表面重构的结构后发送到GPU端；由GPU对表面进行重构，并对重构所得多边形表面进行图形渲染。如此重复上述过程，直至NC代码读取完毕。

图1 数控仿真方法示意图

2 仿真算法实现

2.1 三向Dexel实体建模方法

数控仿真使用实体间的布尔减运算来描述数控加工中刀具切削工件的过程，为此需要对工件和刀具进行实体建模。单向与三向Dexel模型示意图如图2所示。单向Dexel模型通过记录一组平行且等距的光线在实体内部的部分来表示实体，这种方式会造成如图2(a)所示的信息丢失。三向Dexel模型则通过如图2(b)所示的方式，在三个相互垂直的方向进行取样来减少信息丢失，从而提高仿真精度。三向Dexel模型的结构由三组单向Dexel模型组成。

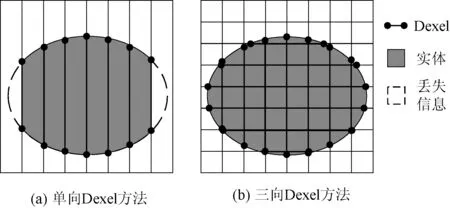
图2 单向Dexel与三向Dexel模型示意图

2.1.1单向Dexel模型的建模

单向Dexel模型在其XY平面上，沿X轴、Y轴正方向以仿真精度P为间隔分布着向Z轴正向发射的光线。每条光线与实体相交的交点都被保存下来，每两个交点之间的线段代表着光线在实体内部的部分，称为一个Dexel。构成Dexel的两个交点中距离XY平面距离较远的为Dexel的上端点，较近的为下端点。同一条光线上的Dexel端点依据距离发射点的距离按升序排列形成的链状结构称为Dexel链。这些Dexel链可以构成一个二维的网格(Grid)结构。假定网格结构沿X轴、Y轴方向分为nX、nY份，则该Dexel模型的分辨率为nX×nY，空间复杂度为O(nX×nY)。

为了压缩Dexel模型所需的储存空间，在记录端点位置信息时仅记录端点到XY平面的距离。需要获取端点的确切坐标时，依据当前Dexel链在二维网格中的位置进行计算即可。坐标为(i,j)的Dexel链上端点的坐标(x,y,z)为：

x=OX+P×iy=OY+P×jz=OZ+dZ

(1)

式中：{OX,OY,OZ}为单向Dexel坐标系中的原点;P为仿真精度;dZ为端点到XY平面的距离。

2.1.2三向Dexel模型的建模

三向Dexel模型的结构由三个相互垂直方向的单向Dexel模型叠加得到。由于数控加工的仿真过程中仅包含布尔减运算，仿真中可能发生布尔运算的范围可以限定在工件胚料的包围盒中。建模时选择在胚料包围盒的X、Y、Z方向分别建立编号为0、1、2的三组单向Dexel模型。第i组单向Dexel模型的局部坐标系{O，eX，eY，eZ}为：

O=BmineX=e(i+1)mod3eY=e(i+2)mod3eZ=ei

(2)

式中：O为单向Dexel模型局部坐标系的原点;eX、eY、eZ为单向Dexel模型局部坐标系X、Y、Z轴的单位向量;Bmin为胚料包围盒的最小点;e0、e1、e2为胚料包围盒坐标系的X、Y、Z轴单位向量。

三向Dexel模型的分辨率NX×NY×NZ为：

NX=ceil[(Bmax.x-Bmin.x)/P]NY=ceil[(Bmax.y-Bmin.y)/P]NZ=ceil[(Bmax.z-Bmin.z)/P]

(3)

式中：Bmax为胚料包围盒的最大点;P为仿真精度。

2.1.3三向Dexel模型的布尔运算

文献[11]详细描述了三向Dexel的并、交、差布尔运算，数控仿真中主要用到的为三向Dexel的减运算。三向Dexel模型之间进行布尔运算时，对双方X、Y、Z方向的单向Dexel模型分别进行布尔运算，即为相对应光线上Dexel的减运算。数控仿真中运算根据刀具Dexel和工件Dexel的相对位置关系，共有图3所示的6种情况。

图3 Dexel间的相减运算

(1) 刀具Dexel与工件Dexel没有任何相交，不需要修改工件Dexel。

(2) 与情况1相同，不需要修改工件Dexel。

(3) 工件Dexel的下端点到刀具Dexel上端点之间的部分被切除。

(4) 刀具Dexel的下端点到工件Dexel的上端点之间的部分被切除。

(5) 工件Dexel被完全删除。

(6) 刀具Dexel的下端点到上端点之间的部分被切除，工件Dexel分裂成两个Dexel。

可以看出，相减产生的新Dexel端点的位置为相应刀具Dexel端点的位置，法线与该刀具Dexel端点法线方向相反。

2.2 刀具扫掠体生成

刀具扫掠体的生成有两种方法：第一种为近似的方法[12]，根据操作的轨迹位置、刀轴角度信息以一定的间距进行插值计算，将扫掠体离散为多个刀具实体；第二种方法为精确的方法[13-14]，通过刀具轮廓线和操作起止点信息精确地计算刀具的扫掠体。精确计算的主要优势在于精度高于前者，劣势在于计算需要更多时间。因此本文选择近似的构造方法，以仿真精度P的一半为间隔插值生成刀具实例，将这些实例的集合作为当前操作所生成扫掠体的近似。

工件与刀具的减运算首先需要生成刀具实例的三向Dexel模型。为了减少建模的运算量，在三向Dexel模型的局部坐标系中生成该实例的包围盒，仅在该范围内进行模型生成。之后从工件三向Dexel模型中减去所生成的模型。其多线程加速运作机制如图4所示。假定共有i个辅助线程，将其分别编号为1,2,…,n，创建辅助线程的主线程也作为0号线程参与运算，则第i号线程负责每个刀具实例包围盒内第k(n+1)+i条Dexel链的构建与对应工件Dexel链的相减运算。

图4 布尔减运算的并行运作机制

2.3 工件的表面重构

三向Dexel模型不适用于可视化，为了获取适合图形设备渲染的多边形表面，需要对实体进行表面重构。本文方法在表面重构时，在CPU端将三向Dexel模型转化为厄米特数据，并在GPU上进行八叉树的构建、特征点的计算、八叉树的化简，以及重构表面的提取。

如图5所示，由于三向Dexel模型的采样精度有限，直接使用表面重构算法(如移动立方体算法，以下简称MC算法)进行表面重构会产生如图5(c)所示的特征丢失。双轮廓(简称DC)算法则可以通过使用由三向Dexel模型提取而来的厄米特数据，通过计算每个体素内部的特征点(图5(d)中的白色点)来还原其丢失特征。表面重构算法的步骤如下：

(1) 在CPU中将三向Dexel数据转换为适合构建八叉树的数据，并将数据送入GPU；

(2) 在GPU上生成能够完全容纳网格数据的最小八叉树；

(3) 并行处理每个叶子节点，对其特征点进行计算；

(4) 对八叉树进行化简，并提取重构表面。

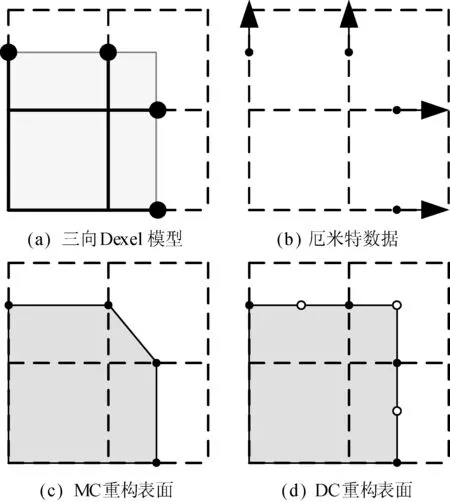
图5 移动立方体与双轮廓表面重构

2.3.1网格信息与赫米特数据的提取

八叉树的建立需要包含完整三向Dexel模型的网格信息，因此需要建立与三向Dexel模型同等分辨率的网格，网格格点及厄米特点的数据结构如图6所示。为了节省显存，格点数据中不保存完整的厄米特点数据，只保存索引值。索引数组的0、1、2号元素分别代表格点X、Y、Z方向的厄米特点。厄米特点的数据单独封装，以一维数组的形式传递给GPU。格点信息的提取通过遍历三向Dexel模型中的Dexel完成，如图7所示。首先为每个Dexel的端点分配索引值，并将其所经过的格点均设置为内部格点，在最靠近Dexel上下端点的内部格点处记录对应Dexel端点的索引值。

图6 格点与厄米特点的数据结构示意图

图7 从三向Dexel模型中提取网格信息

2.3.2八叉树的建立

双轮廓法结合自适应精度八叉树可以简化生成的表面，有效减少表面包含三角形的数量，提高渲染速度。本文使用的在GPU端运行的并行八叉树生成算法[15]能够在节约显存的同时提升算法的运行效率，可以极大缩短八叉树构建时间。所构建八叉树的最大深度由传入网格数据的尺寸决定，大小为能够完全容纳网格的最小八叉树。由于GPU并不支持动态内存分配，每层节点所需要的存储空间需要提前分配。该方法首先构造叶子节点，并从底层向上依次进行八叉树的构造。若一个叶子节点为非空叶节点(8个角点中既包含内部格点又包含外部格点的叶节点)，则构建一个新的节点，使用原子计数器对其进行编号并使用查询表来存储子节点与父节点之间的关系。在建立八叉树的过程中需要统计构建叶节点数量，用于为后续步骤会用到的二次误差方程数据分配存储空间。八叉树构建完成后，使用构建的八叉树来进行特征点的计算和八叉树的简化。

2.3.3特征点的计算

双轮廓法中特征点的计算是通过求解叶节点的二次误差方程(Quadratic Error Function，QEF) 得到的。QEF的定义如下：

(4)

式中：pi、ni代表着该叶子节点所对应体素边上厄米特点的位置与法线，可以通过查询该体素8个角点对应格点的索引数组得到。将式(4)转化为矩阵形式并展开为：

E[x]=xTATAx-2xTATb+bTb

(5)

式中：矩阵A代表着体素边上厄米特点的法线ni;向量b的第i个分量为nipi，求解方程最小值所得的x即是该体素的特征点。方程的具体解法参照文献[7]。为了方便后续八叉树的简化及多边形表面的提取，由体素构造出的QEF及其计算结果被单独封装在QEF类中，存储于事先分配好的存储空间中并由原子计数器为其分配索引值。构建完成后，在八叉树节点中记录其QEF的索引值以建立对应关系。所有叶节点的特征点计算完成后，对八叉树进行简化。

2.3.4八叉树的化简与重构表面的提取

对八叉树进行化简的目标是使用更少的三角形来表示重构表面的平缓区域，在保持图形特征不改变的前提下减少渲染三角形的总量，以降低图形设备的负担。首先将同属于一父节点的8个叶节点的QEF中各项相加，若计算相加所得QEF解得的误差值小于一给定阈值，则可以对这些叶节点进行化简。化简后将叶节点的特征点修改为父节点的特征点，并将父节点标记为伪叶子节点，如此往复由底向上逐层进行化简。

化简完成后遍历八叉树的每个叶节点，对其进行表面提取。将每个叶节点的特征点提取到数组中，使用原子计数器为其分配索引值。最后根据叶节点之间的拓扑关系设置索引，完成多边形表面的提取。

3 仿真结果

数控仿真系统软件使用C++编写CPU端程序，使用OpenCL编写GPU端程序，使用OpenGL进行图形渲染，运行硬件环境为Intel Core i7-3770 四核CPU，12 GB内存，2 GB显存的NVIDIA GeForce GTX 660 Ti显卡。

仿真实验1测试不同建模方法的仿真效果，如图8所示，其中：(a)、(c)为使用单向Dexel建模方法，(b)、(d)为使用三向Dexel建模方法。可以看出，应用三向Dexel建模方法后消除了使用单向Dexel建模方法时的阶梯化问题。

图8 不同建模方法的仿真效果对比

仿真实验2为双轮廓法对特征修复的验证，图9、图10分别为该方法对雕像模型和叶轮模型丢失特征的修复效果。图9(a)、图10(a)为使用三向四面柱(Tri-Quadpillars，简称TQ，将文献[9]中的算法扩展到三维得到)算法进行表面重构得到的结果图；图9(b)、图10(b)为使用双轮廓法进行表面重构得到的结果图。可以看出，使用双轮廓法后，由特征丢失导致的毛刺、锯齿问题得到了修复，同时能够更好地保存尖锐棱角等信息。

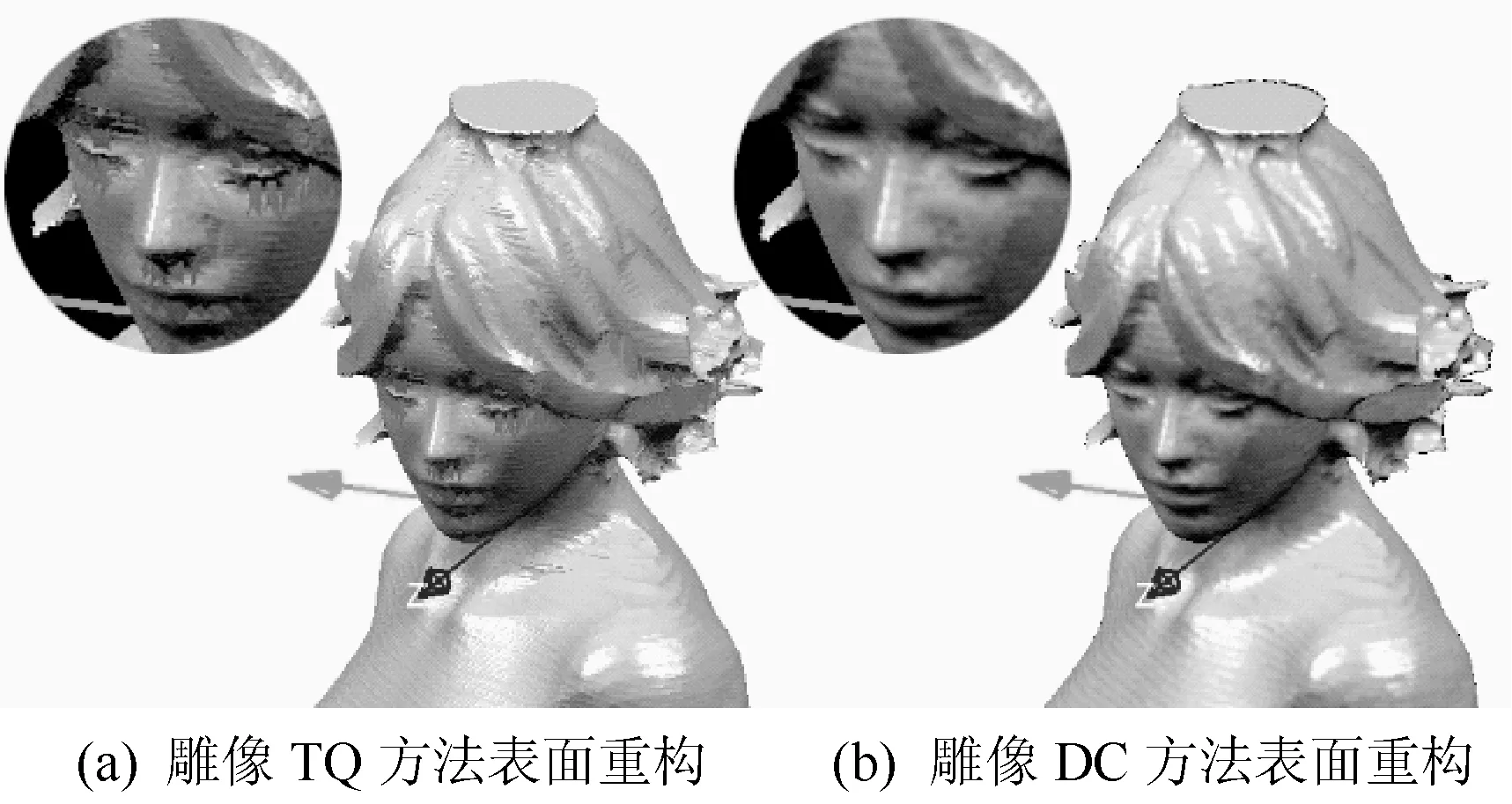
图9 双轮廓法对雕像模型丢失特征的修复效果

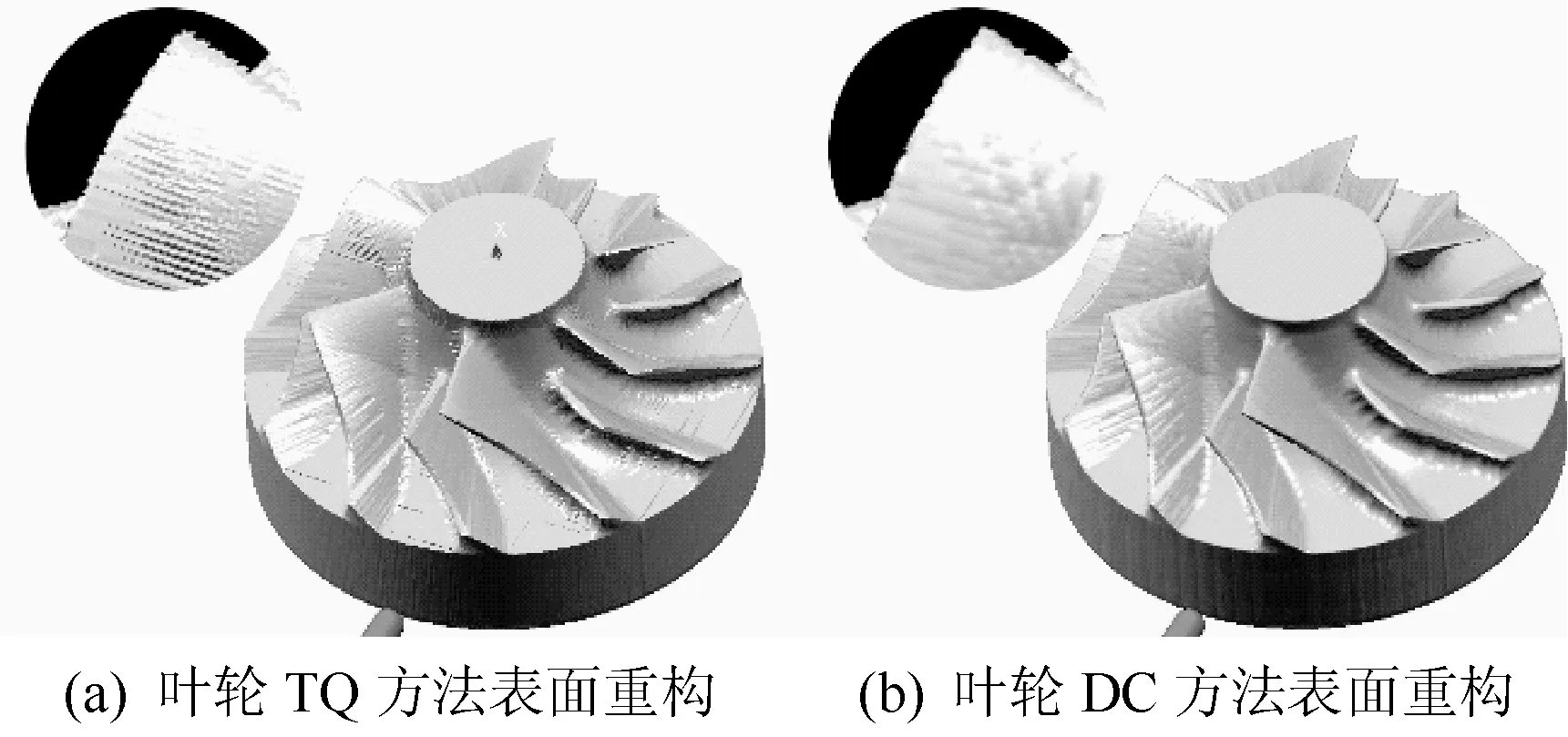
图10 双轮廓法对叶轮模型丢失特征的修复效果

仿真实验3测试仿真方法加速前后的运行效率。表1为仿真实验3中所使用的实验对象，实验共使用两组数控加工程序：第1组为雕像的加工，第2组为叶轮的加工。

表1 仿真所用实验对象

表2所示为多线程加速前后表面重构的平均时间。可以看出，多线程加速比单线程双轮廓法表面重构快232%～289%。由于双轮廓算法中八叉树构建所耗费的时间在算法总耗时中占比最大，且该部分并行化程度较高，多线程加速能够获得较高的加速比，但由于双轮廓算法本身时间开销较大，仅在CPU端进行加速仍然难以满足实时仿真的要求。

表2 多线程加速前后表面重构平均时间

表3展示了GPU加速前后表面重构平均时间。可以看出GPU加速比CPU下多线程加速双轮廓法表面重构快5～15倍。完全在GPU端进行的双轮廓算法在重构对象分辨率升高时，因网格数据与厄米特数据的增大而增加了GPU的读写压力，造成了加速比的下降，但仍然能满足实时仿真的要求。

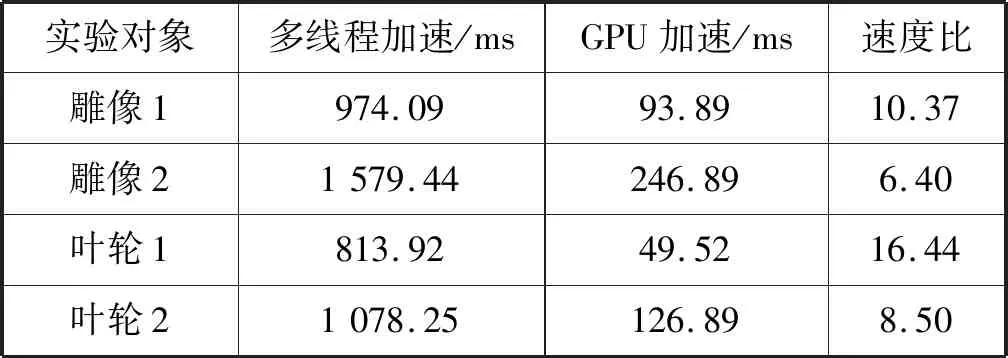
表3 GPU加速前后表面重构平均时间

4 结 语

本文实现了一种并行化的基于三向Dexel的数控仿真方法。采用三向Dexel建模方法提升仿真的精度，使用双轮廓法来获取更加真实的重构表面。该方法的创新之处在于其通过双轮廓算法修复因表面特征丢失造成的毛刺、锯齿问题，并通过将多线程加速、GPU加速与双轮廓算法结合起来，使得表面重构的速度相对于多线程的实现提升了5～15倍，能够在满足仿真实时性要求的前提下，修复由于三向Dexel模型采样问题造成的特征丢失，从而提高仿真的真实度。