基于改进PCA算法的振荡故障根因定位方法
2020-11-12陈孟婷付晓薇
陈孟婷 付晓薇* 李 曦
1(武汉科技大学计算机科学与技术学院 湖北 武汉 430065) 2(智能信息处理与实时工业系统湖北省重点实验室 湖北 武汉 430065) 3(华中科技大学人工智能与自动化学院 湖北 武汉 430074)
0 引 言
近年来,工业系统领域的振荡故障越来越受到关注,故障根因定位技术成为了该领域的热点研究问题。故障根因定位是指通过一定的手段来寻找出处于异常状态下的系统故障点,进而为系统损坏的及时处理提供参考作用[1]。现有的故障根因定位方法主要分为基于模型和数据驱动两类[2-4]。基于模型的方法需要了解生产制造系统的机理,从而建立起准确且可靠的解析模型,主要包括状态估计法、参数估计法等;数据驱动方法以多元统计分析为基础,融合了信号处理、人工智能等方法,不需要准确的机理模型,仅依靠系统运行过程中的大量测量数据挖掘出有用的潜在信息,实现故障监测[5]。随着传感器技术和数据采集、存储方法的快速发展,数据驱动方法越来越受到工业界和学术界的关注。
多元统计分析方法是数据驱动的重要组成部分,它利用过程变量之间的相关性进行分析和复杂数据的简化[6-8]。常见的方法有PCA、偏最小二乘法(PLS)、主元回归方法(PCR)等。其中PCA的应用最为广泛,使用Hotelling’s T2指标和SPE指标来进行故障的甄别。然而,PCA方法无法进行故障根因判别,需要提出一种新的方法在故障检测后准确找到故障的根因。
作为以上方法的扩展,研究者们提出了局部LPCA[9]、核PCA[10]和混合PCA[11]等方法。但是,时变的动态信息可能对不同的变量间存在高度的耦合性[12]。一些变量在表现出强烈的动态特性时,会影响到其他变量的连锁反应,这给故障的根因定位带来了难度。同时,上述方法将所有变量都置于同样的动态水平来处理,这对于故障的根因定位实现是没有实际效果的。
格兰杰因果关系检验(Granger Causality Test,GCT)旨在检测两个时间序列之间的因果方向[13-14]。作为一种全新的特征提取方法,GCT能够从时序信号中找出两个变量之间的相互因果关系,其基本原理是建立自回归模型,在控制过去值条件下,估计过去值对当前值的预测精度。
本文在此基础上提出改进的PCA方法,即PCA-GCT方法,将原有方法进行扩展,使其能够寻找出所发生的故障根因位置。
1 振荡信号显著性指标
1.1 振荡信号的识别
已知在时间[t0,t1]上连续变化的m维输入:
x(t)=[x1(t),x2(t),…,xm(t)]
(1)
假设存在函数g(x)=[g1(x),g2(x),…,gm(x)],可以得到输出信号s(t)=[s1(t),s2(t),…,sm(t)],其中si(t)=gi(x(t))。振荡信号检测如下:
(2)
式(2)表示当输出信号在全局范围内,时间[t0,t1]上最大值与最小值之和isO。在阈值R设定合理时,当阈值R>isO时,则认为无振荡信号出现,反之,则会出现振荡信号,表明工业过程出现故障。而阈值R的设计则需结合所研究工业系统的固有特性来实现。
1.2 振荡显著性指标OSI
工业过程当中存在大量传感器测量变量与振荡无关。为提高振荡故障根因定位准确性,基于PCA方法计算振荡显著性指标(Oscillation Significance Index,OSI),从原始过程数据中筛选出振荡变量。OSI表示信号振荡的强烈程度,计算如下:
(3)
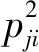
2 改进的PCA算法
2.1 PCA算法

(4)
k的个数表示原观测数据矩阵拟降维后的维数,其最优值可以根据方程的累计比例获得,即:
(5)

依据PCA结果可以对OSI进行选择,筛选出振荡变量,以缩小振荡因果分析的范围。
2.2 格兰杰因果检验
系统运行历史数据由多个过程变量的时间序列数据组成,取其中任意两个过程变量的时间序列xi(t)和xj(t),分别对xi(t)和xj(t)所有滞后项xi(t-k),xj(t-k),k=1,2,…,l作回归,建立预测xi(t)的完整模型:
(6)
式中:a为模型系数;ei(t)为模型预测误差;l为模型阶数,定义模型中包含滞后项个数。
对应上述完整模型定义,排除变量xj(t)的滞后项再作回归,建立预测xi(t)的受限模型:
(7)
式中:ei(j)(t)是指不考虑xj对xi的预测所得的模型预测误差。
如果模型预测方差var(ei)显著小于var(ei(j)),其统计意义是结合xj的过去值,xi的预测更为准确,即xj对xi产生格兰杰因果关系。其因果影响程度可以通过受限模型预测误差与完整模型预测误差比率指数来量化:
(8)
将格兰杰因果关系推广至多变量情形下,对工业过程原始过程数据建立向量自回归(VAR)模型,表示为:
(9)
式中:[x1(t)x2(t) …xn(t)]T表示n=1,2,…,24过程变量时序数据;l定义VAR模型滞后阶数;[e1(t)e2(t) …en(t)]T分布表征x1(t),x2(t),…,xn(t)的模型预测误差。


表1 n个过程变量方差矩阵

(10)
在进行格兰杰因果关系推论之前,应用F检验验证其统计显著性。提出假设“xj对xi不存在因果关系”,在该条件下统计量服从自由度为lr和(m-lur)的F分布。在选定的显著性水平α(值设为0.05)上计算F值,若P值小于α,即F值超过临界值Fα,则拒绝零因果假设,表明xj是xi的原因。
(11)
式中:m为观测样本容量;RRSr和RRSur为受限模型和完整模型的残差平方和;lr等于xj滞后项阶数,即受限模型中待估参数数量;lur为完整模型中待估计参数的个数,满足lur>lr。
以上描述针对的是时域下的格兰杰因果检验方法,为了进一步分析在特定频率f下振荡变量间的相互作用程度,在频域中分解基于时域格兰杰的因果关系,得到因果频谱图。计算频率f下从xj到xi的频域格兰杰因果关系度量值采用参考文献[13]的方法。
综上,可以通过PCA方法降低数据的维度,从而便于故障数据间的相关性分析。在此基础上,与GCT方法相结合后,通过格兰杰因果关系分析,达到使用PCA-GCT进行故障根因定位的目的。
3 振荡故障定位的实现
GCT通过定量估计过程变量间相互影响程度实现振荡传播路径分析,具有实现简单、可解释性强等优点。然而,GCT分析是基于VAR模型的,这要求多变量时间序列数据输入必须满足广义平稳性要求。由于不同运行状态切换,系统原始运行数据中存在线性变化,直接使用GCT方法会影响振荡源的识别效果。为了确保振荡因素作为原始数据的主要信息,同时满足VAR建模要求的广义平稳性,对原始数据作平稳化预处理如差分变换操作,消除时间序列时变趋势。
SOFC系统振荡根因定位分为两个阶段:
1) 离线实现。
根据国内已溃八座水库大坝统计资料,结合已有的研究成果,通过试算与数理统计分析数据,在风险人口死亡率值的确定中考虑了一个修正系数β,建议取值β=1.4。
步骤1采集工业系统的过程数据,获取数据集X0;
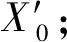
步骤3将处理后的数据代入PCA算法,即将数据代入式(4)和式(5),获取影响振荡的主要数据元素;
步骤4获取降维的简化数据后,选出各振荡变量代入式(10)和式(11)进行因果分析的判断;
步骤5若能准确分析出故障的根因,则认为达到了根因定位的目的,则进入步骤6,否则重新进行步骤4;
步骤6根据实际工业系统运行经验设计合理的振荡信号阈值R。
2) 在线实现。
对比振幅isO和阈值R,若isO>R,则引入PCA-GCT算法进行故障根因定位。
本文方法结合PCA和GCT的优点,可抓住工业系统的动态过程信息,具体流程如图1所示。
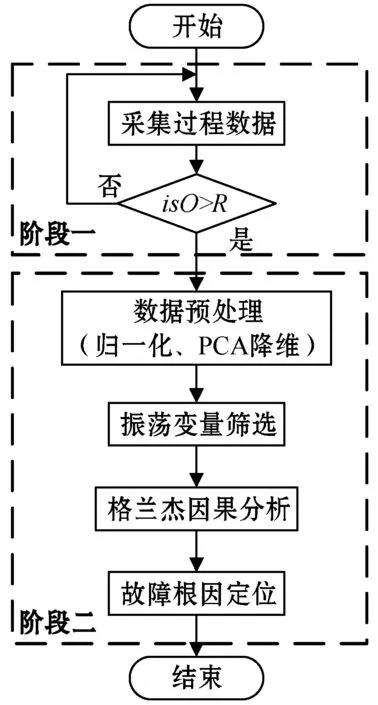
图1 振荡故障定位流程图
4 应 用
4.1 SOFC系统工作过程介绍
采用1 kW带水蒸气重整SOFC发电系统的过程数据进行振荡故障定位分析。该独立发电系统由SOFC电堆集成热箱(含重整器、燃烧室与换热器)与冷箱(含风机、功率变换器与控制系统)等外围部件(Balance of Plant,BOP)组成,图2为系统流程示意图,具体的系统描述可参考文献[15]。图2给出主要传感器分布情况,这些传感器测量包括气体流量、压力以及各组件内部温度共21个过程变量数据。
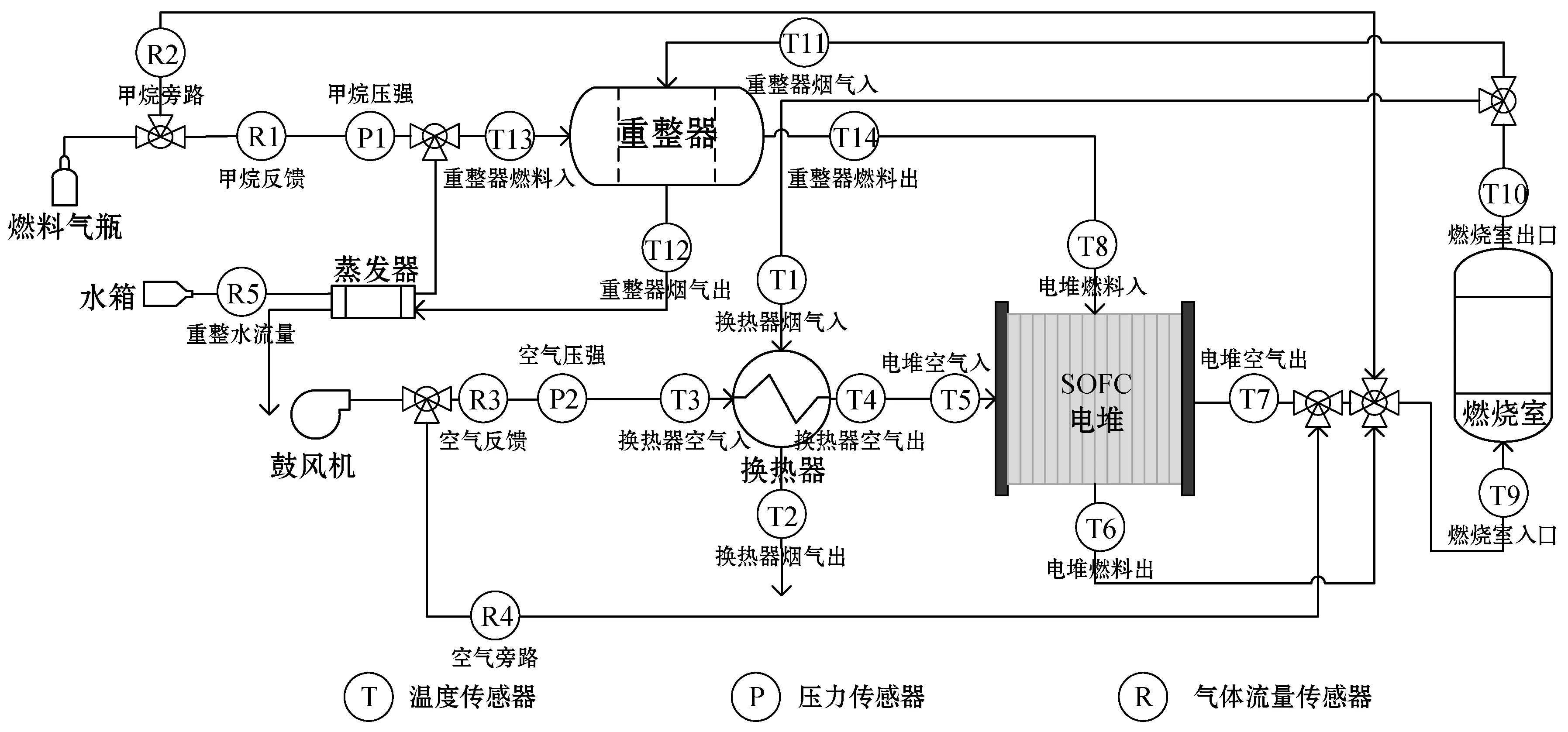
图2 水蒸气重整SOFC发电系统流程示意图
从系统中每隔1 s采集24个过程变量数据用于振荡故障分析,包括上述传感器数据以及电堆电压、电流和功率三组电特性数据,图3为过程数据归一化时间趋势曲线。可以看出,将近一半的过程变量都出现了不同程度的振荡。由于整个发电过程涉及变量众多、控制回路关联性复杂,振荡信号可以很容易地在多个控制回路中传播,因而很难确定故障源。
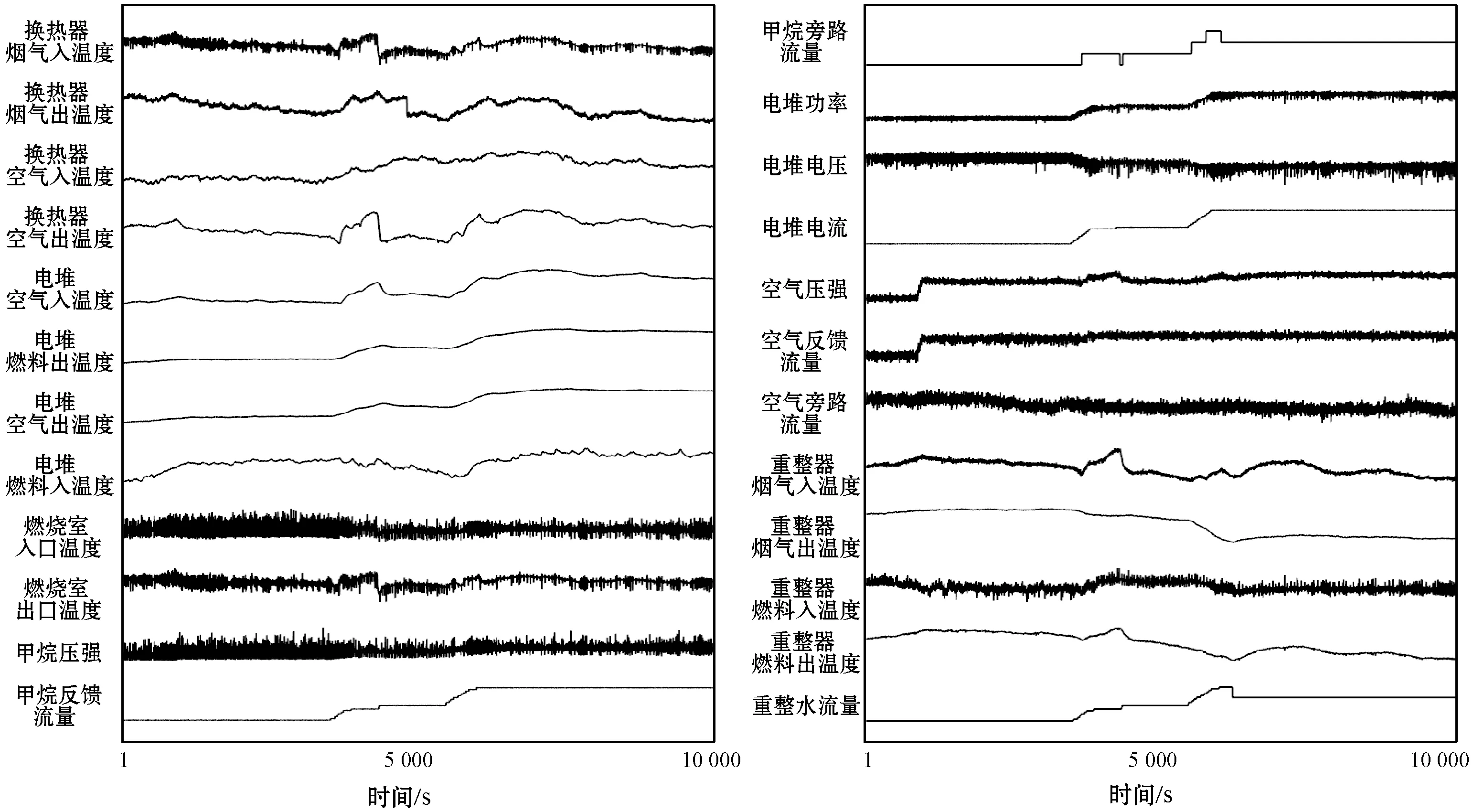
图3 系统振荡过程时间趋势图
4.2 仿真实验结果与讨论
1) 振荡变量的筛选。对原始传感器数据作归一化处理,并采用PCA降维,如图4所示。24个原始过程变量降维至5维主元,其累计贡献率已经达到95%以上。
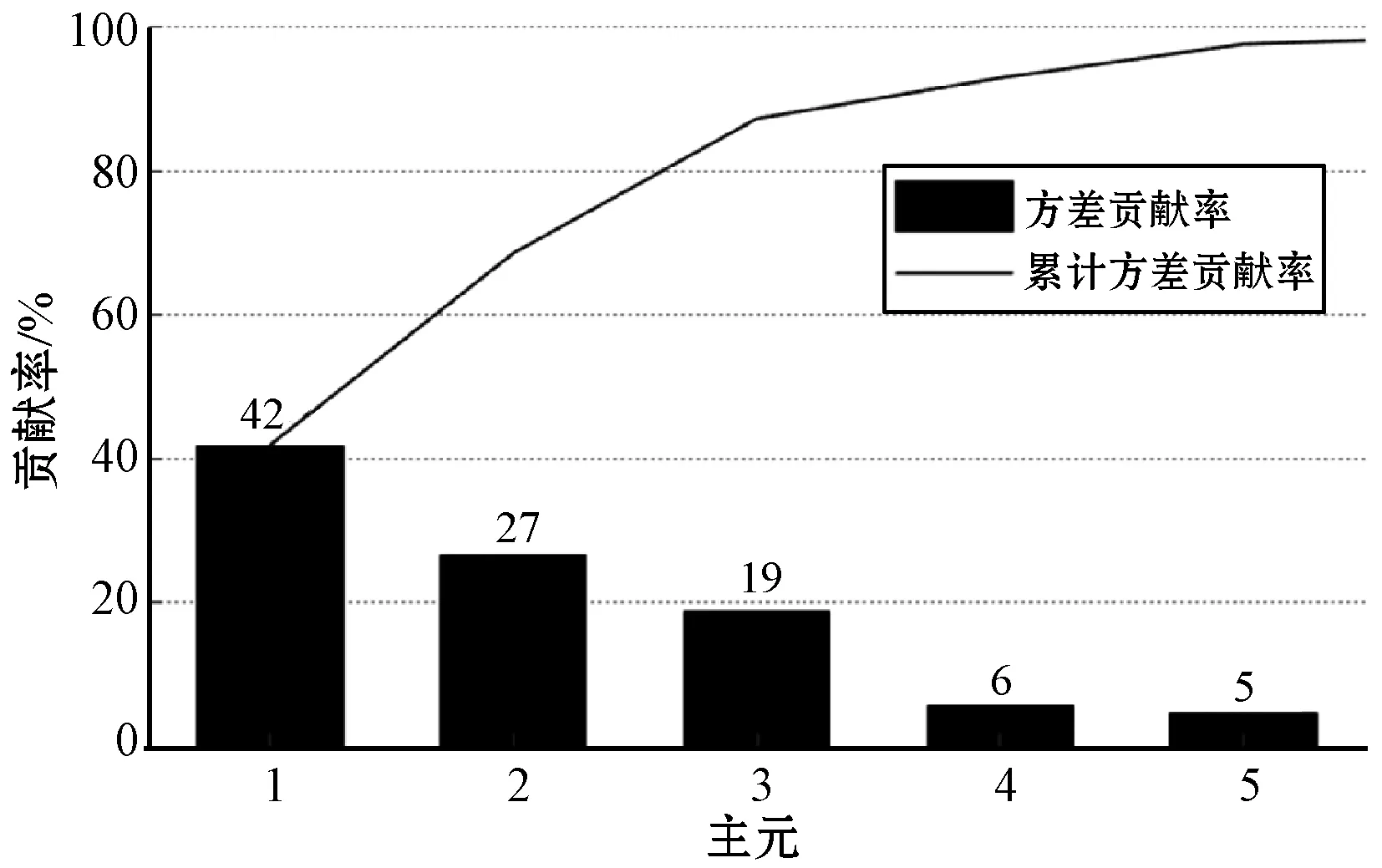
图4 PCA降维图
以方差贡献率所占百分比大于10%为条件,在所有过程变量中筛选出具有显著振荡的变量,结果如图5所示。振荡变量包括燃烧室入口温度、甲烷压强、电堆电压、空气旁路流量,以及重整器燃料入温度。结合图5给出的所有过程变量时间序列图来看,振荡变量筛选结果是其中受振荡影响最大的五个变量。

图5 振荡显著性指标结果
图6(a)为筛选出的振荡变量原始数据曲线。可以看出,除燃烧室入口温度外,其他振荡变量均表现出不同程度的时变趋势,其中空气旁路流量和重整器燃料入口温度呈现出不规则趋势变化。为了确保时间序列格式数据的广义平稳性,提高定位结果的可靠性,在数据平稳化预处理环节对原始非平稳时序数据进行一阶差分操作(即xt=xt-xt-1),振荡变量平稳化结果如图6(b)所示。可以看出,各振荡变量的趋势变化被有效过滤,同时完好地保留了振荡特性。例如,燃烧室入口温度原始数据初期具有明显趋势变化且振荡幅度最大,平稳化处理后数据的前期趋势基本消除,同时保留最大振荡幅度特征。
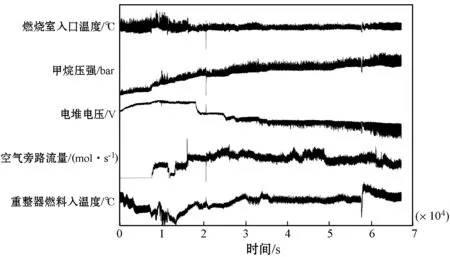
(a) 振荡变量原始数据曲线
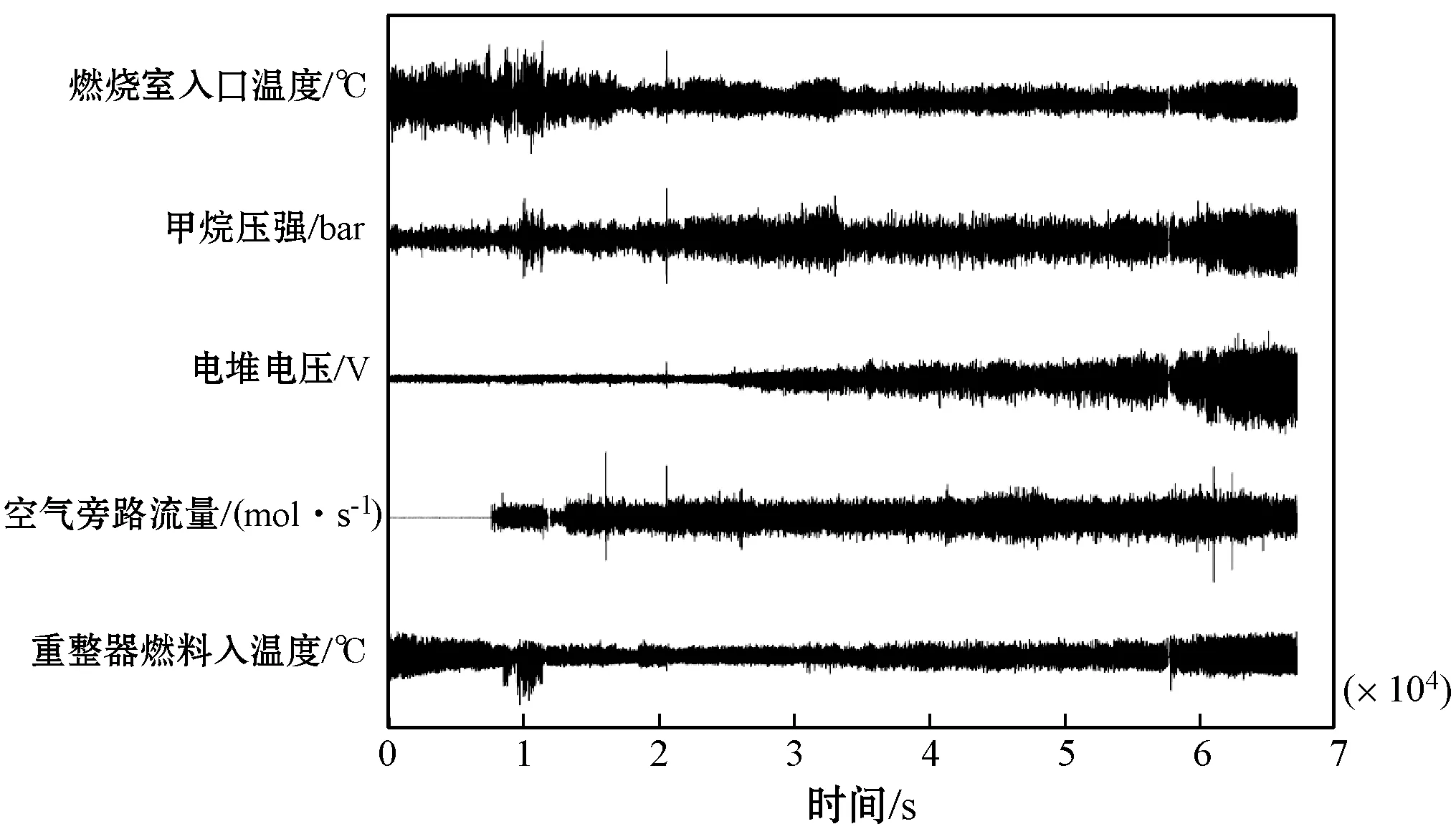
(b) 振荡变量平稳化结果图6 振荡变量曲线图
2) 振荡传播路径分析。通过对筛选出的振荡变量进行格兰杰因果检验,分析振荡传播路径。主要内容如下:
(1) 对五个振荡变量进行时域格兰杰因果分析,得到时域因果矩阵如表2所示。因果矩阵中任意位置表示从第列变量到第行变量的因果度量值。例如,位置表示甲烷压强对电堆电压的格兰杰因果度量值为0.284 1,是所有因果度量值中最大的,这表明甲烷压强对电堆电压的振荡影响最大。表3给出每组因果关系的F检验结果P值,当P值小于显著性水平α时,该因果推论成立,在表3中以加粗形式标出,相应因果度量值在表2中加粗显示。结合因果矩阵和假设检验结果,确定具有因果关系的变量对。
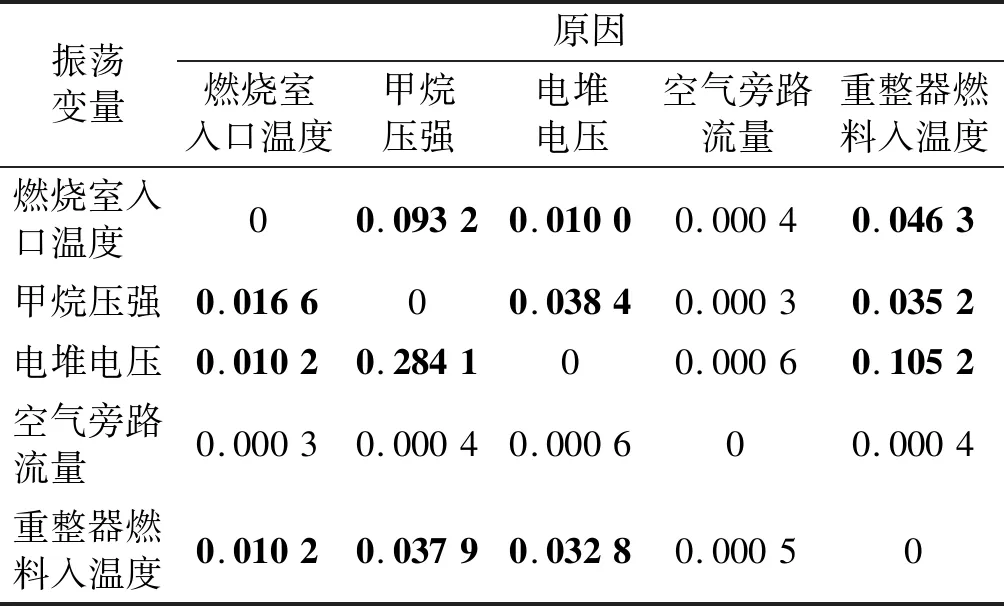
表2 时域格兰杰因果矩阵
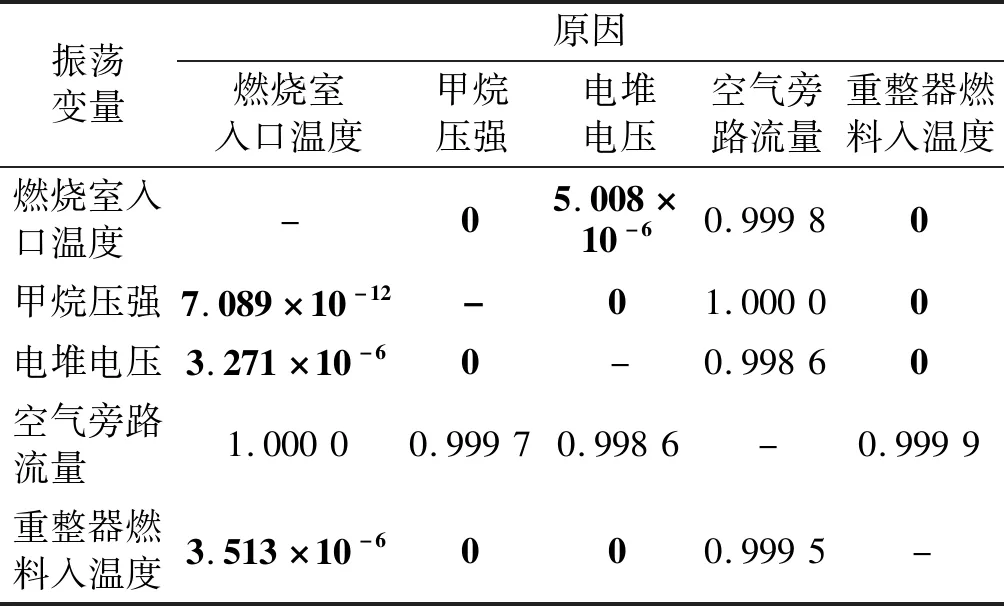
表3 显著性检验结果P值
值得注意的是,空气旁路流量与其他变量间的因果度量值都非常小,F检验结果显示对应因果假设不成立,这表明空气旁路流量不参与上述振荡传播。结合过程知识,可以给出合理解释:在空气管道上增设的冷空气旁路,其目的是通入足量的冷空气,实现对电堆入口空气温度有效控制,从而保证电堆处于热安全状态。相比于过量的空气反馈供给,燃料供给才是引起电堆放电异常波动的关键。另外,从图3可以看到,与空气旁路流量一样,空气反馈流量和空气压强也受到了振荡影响,但由于受影响程度较小在振荡变量筛选环节被过滤掉。由此可以推出鼓风机故障导致的空气量波动,与甲烷压力无关。
(2) 在时域格兰杰因果关系基础上,通过频域进一步分解得到因果谱,如图7所示。图中给出了振荡变量在不同频率下对其他变量的因果度量值,即(i,j)子图表示第j个振荡变量在各频率上对第i个变量的振荡影响程度。结合表2中因果关系成立的变量组合对应位置来看因果频谱图,图中系统振荡频率范围在0.00~0.05 Hz,除空气旁路流量外,其余振荡变量两两间均存在因果反馈,这反映了系统的强耦合特性。甲烷压强和重整器燃料入温度对燃烧室入口温度的波动均表现出显著性因果影响,二者无明显差异。但同时可以发现,甲烷压强在振荡频率范围内对电堆电压影响最大,0.006 Hz处达到最大值0.47,远高于其他原因(包括重整器燃料入温度)引起电堆电压变化的因果值。此外,由于检测甲烷压强的压力传感器与检测重整器燃料入温度的热电偶部署在同一管道上且十分靠近,两过程变量对另一变量的变化具有相当的预测能力。又因为位置临近振荡源,两变量数据振荡更为活跃,相互预测能力不高,由此推断甲烷压力不稳定是振荡故障源,直接影响到重整器燃料入温度波动,而后导致电堆电压抖动,最后引起燃料入口温度波动性变化。
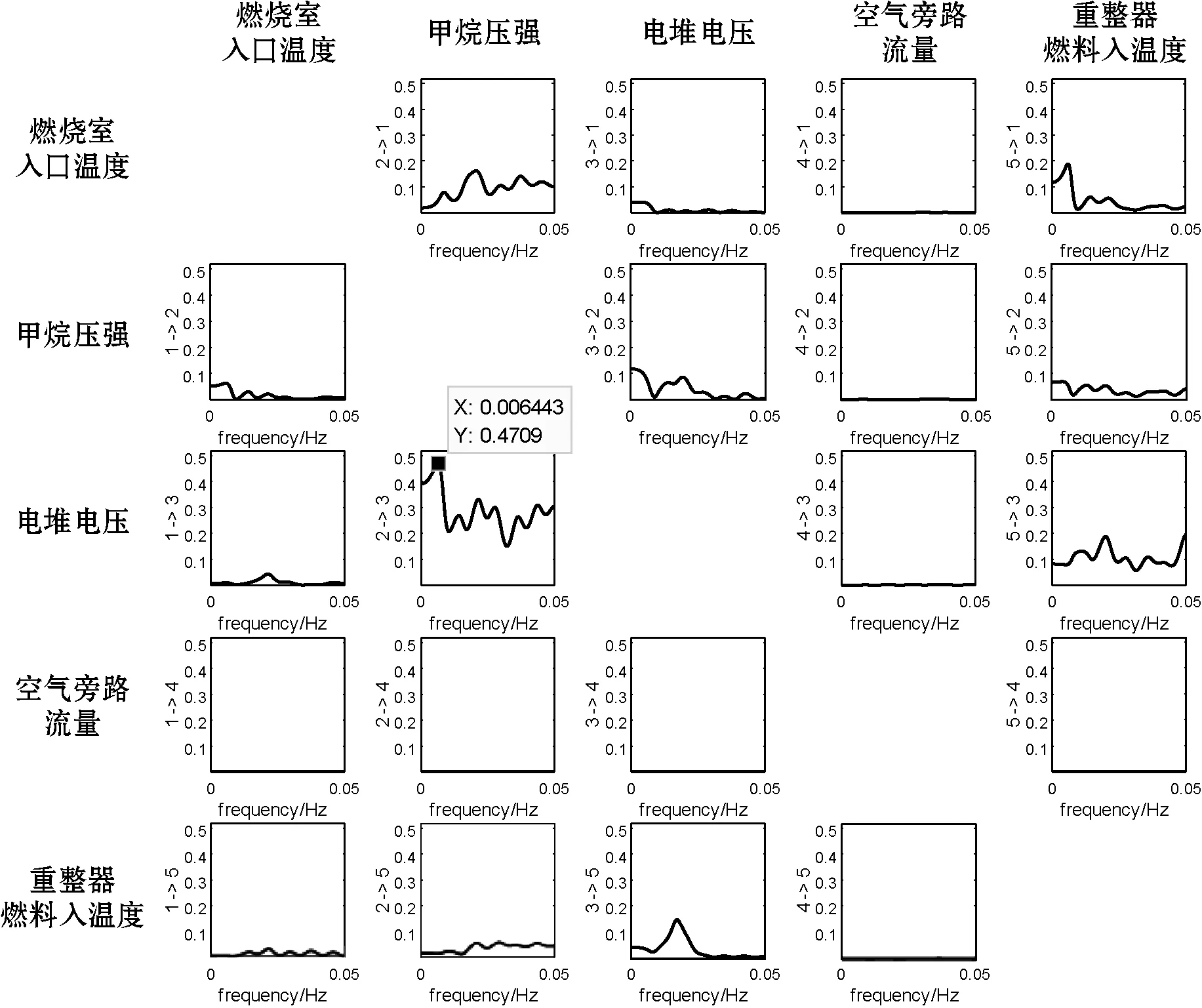
图7 频域格兰杰因果图
依据SOFC发电系统各组件连通性规则,如图2所示,该实例中振荡故障传播路径为燃料供给→重整器→电堆→燃烧室,振荡源为甲烷压力不稳定。甲烷反馈流量没有明显振荡,可以排除燃料供给端流速不稳定原因。结合专家经验和事后验证实验得出该实例故障根因是重整反应水蒸气波动。因重整反应水蒸气和甲烷供给管道相通,水蒸气的波动影响到腔室内压力波动,进而影响到甲烷压力的波动。由于蒸发器内部水蒸气的波动无法用传感器监测得到,因而振荡故障源定位在甲烷压力不稳定是最接近实际故障根因的结果。
5 结 语
本文在分析振荡信号显著性指标的基础上,提出一种改进PCA方法,使其能够判断所产生的复杂工业过程振荡信号的根因。该方法结合PCA和GCT的优点,能抓住系统的过程动态信息。最后,将改进的PCA方法应用于复杂的SOFC发电系统上,验证了所提方法对SOFC发电系统振荡信号根因定位的有效性。同时,该方法为其他复杂工业过程的故障根因定位提供一种新思路与解决方案。
