基于水导激光平面缩流喷嘴内流场仿真研究
2020-11-11杨林帆黄宇星龙芋宏
杨林帆,焦 辉,黄宇星,梁 恩,龙芋宏
(桂林电子科技大学 机电工程学院 广西制造系统与先进制造技术重点实验室,桂林 541004)
引 言
稳定高速射流具有特征尺寸小、集束性强、瞬间动能大等特点,被广泛应用于高压水射流、水利针刺以及水导激光加工工艺。喷嘴孔内的空化和液流反转对射流的质量和流动状态有着重要的影响,国内外很多学者进行了大量的理论和实验研究。1936年,OHNESORGE[1]做出了第1个重大贡献,他提出了在不同雷诺数和韦伯数下工作的圆边喷嘴的流态分类。WAGNER等人[2]研究了小孔喷嘴直径与水射流的速度对水射流的稳定长度的影响。在此基础上,国内FU[3]和LEI[4]等学者分别对水导激光的水射流破裂长度与出口速度进行模拟探究。SUN[5]和LIN[6]等人通过改变喷嘴入口压力获得缩流型水束,最大压力可达5MPa。五邑大学YANG等人[7]对光液耦合腔体进行多场仿真,获得喷嘴直径为0.4mm,水束压力为20MPa的水导激光切割钢化玻璃的工艺参量。ZHANG等人[8]通过实验的方式对低气压包裹下的低压水束稳定因素进行探究,验证了气缩型水导激光工艺的可行性。TOMIYAMA等人[9]研究了2维喷嘴不同工况下空化对射流的影响,指出了空化、超空化和水力翻转等不同的产生流态。ANNONI等人[10]通过测量金刚石孔口的流量系数,研究了金刚石孔口几何形状对上锥和下锥几何孔口切割性能和射流稳定性的影响。LU等人[11]从理论上分析了类层流射流可以改善激光能量的分布。ZHANG等人[12]通过理论研究发现海洋中非均匀偏振光束的光强分布主要受海洋湍流的影响。TAMAKI[13]和HIROYASU[14]等人的实验研究表明,孔内空化的发生对射流的破裂有重要的促进作用。空泡的破裂会增加气流中的扰动,导致射流更快地破裂。TAFRESHI等人[15]对空化和水力翻转进行了数值模拟,并分析水利针刺喷嘴内部流场。结果表明,当水力翻转发生时,由于下游空气向上进入喷嘴,气蚀消失,类层流水束形成,进一步促进射流破碎长度的延长,产生的收缩射流不再遵循Ohnesorge的射流状态分类机理。高速射流生成和快速动态结合过程的小特征尺寸,目前通过实验方法验证非常困难,面对微小尺寸的瞬态两相层流,计算流体动力(computational fluid dynamic,CFD)数值模拟可以对毛细喷嘴内部流场有更好的理解和优化。本文中对不同的喷嘴几何参量和供液压力0MPa~50MPa范围下喷嘴内部流场模拟计算,进行缩流型水束的形成因素系统化分析总结,为高压供液系统下的水导激光工艺所需的稳定光滑水光纤形成,提供参量依据。
1 微水导激光喷嘴模型
1.1 模拟理论
有限元模型基本原理是将求解域离散成大量控制单元,通过对这些控制单元的积分,可以将控制偏微分方程转换为它们的代数等价形式,然后用迭代法求解得到的代数方程组。本研究中采用有限元CFD中流体体积模型(volume of fluid model,VOF)层流两相流模型,在整个区域内求解一个动量方程,得到液体和空气共用速度场。
连续性方程为:
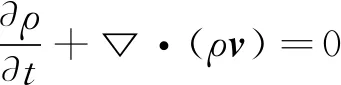
(1)
式中,ρ为流体的密度,t为时间,v为流体空间上的速度矢量和。
动量方程为:
▽·(μ(▽v+▽vT))+ρg+F
(2)
式中,p为压力项,μ为流体动力粘度,g为液体的惯性加速度,F为液相边界表面张力。动量方程通过材料属性ρ和μ受所有相的体积分数影响。
为追踪两相界面,结合(1)式、(2)式求解液相体积分数连续性方程。
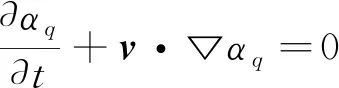
(3)
式中,αq为第q相流体的体积分数。
为得到更加精确的界面模拟结果,采用几何重构方案,表面张力以及惯性力加入模拟计算,并利用压力隐式拆分算法(pressure implicit split operator,PISO)对压力场和速度场进行耦合,得到最佳收敛性。
1.2 计算模型
水导激光工艺最初由RICHERZHAGEN深入研究,形成完整的加工工艺[16]。其工作原理如图1所示。
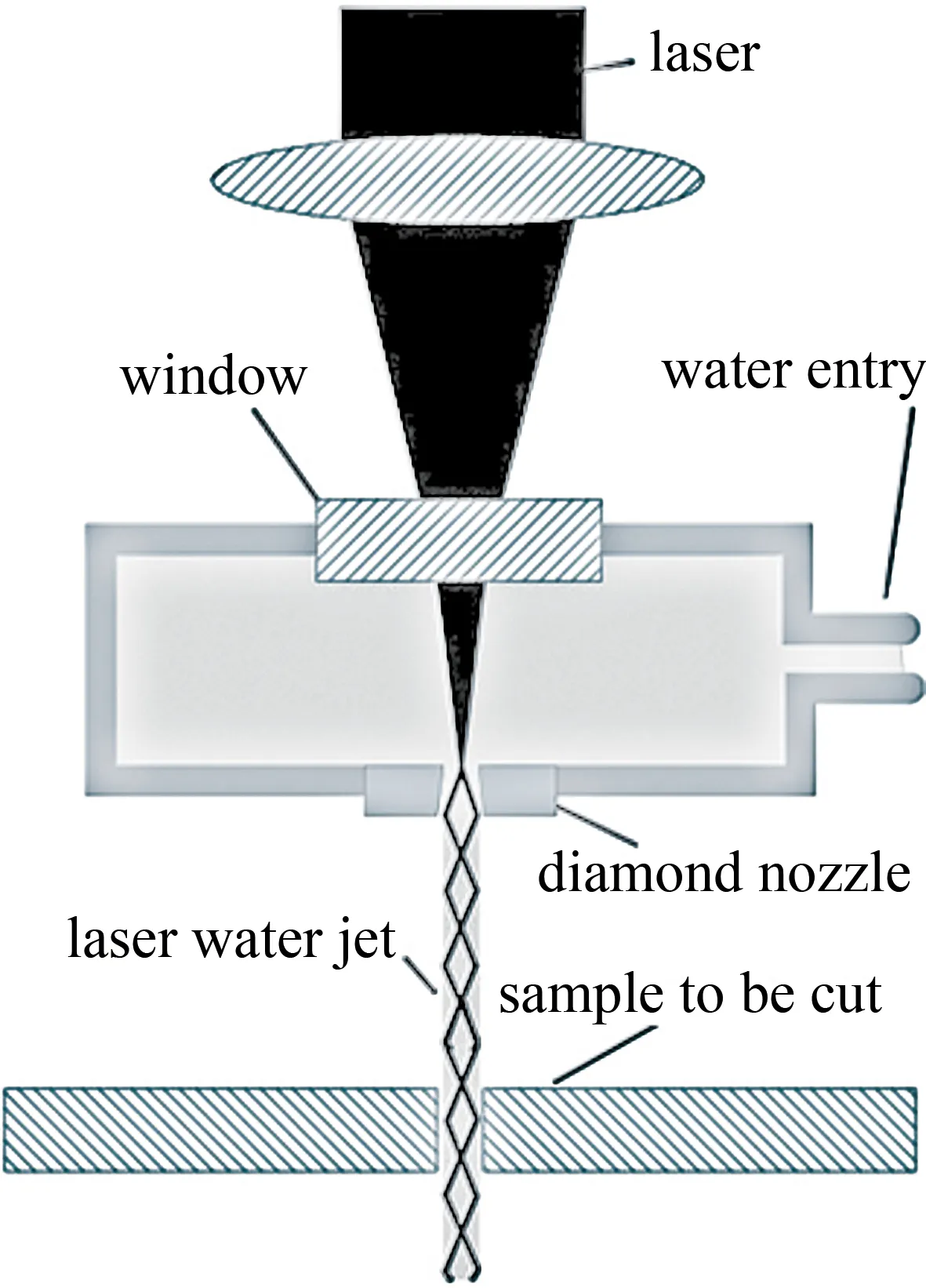
Fig.1 Principle of water-laser coupling unit
水光耦合腔体的高压工作环境对喷嘴上端有冲击腐蚀影响,减短其工作时长,毛细段可以有效解决冲击腐蚀问题,锥角段则为承压考虑。因此本研究采用毛细带锥角结构,如图2所示。喷嘴内部流场长L=
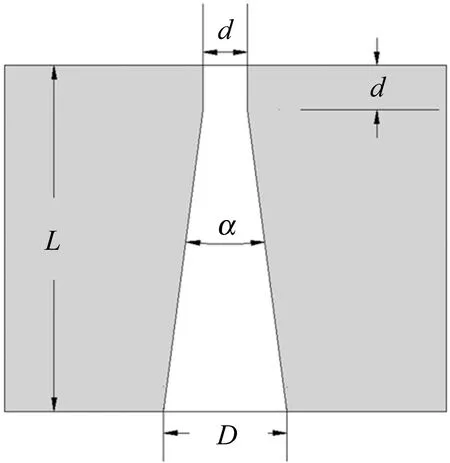
Fig.2 Schematic diagram of nozzle structure with capillary tapered angle
1mm,入口直径d分别为0.128mm,0.07mm,0.03mm,出口直径D和锥角α=15°。
模型选取实际尺寸,整个区域包括压力入口,壁面和压力出口,如图3所示。参考实际物理条件添加薄水层,喷嘴内部流场初始充满空气。
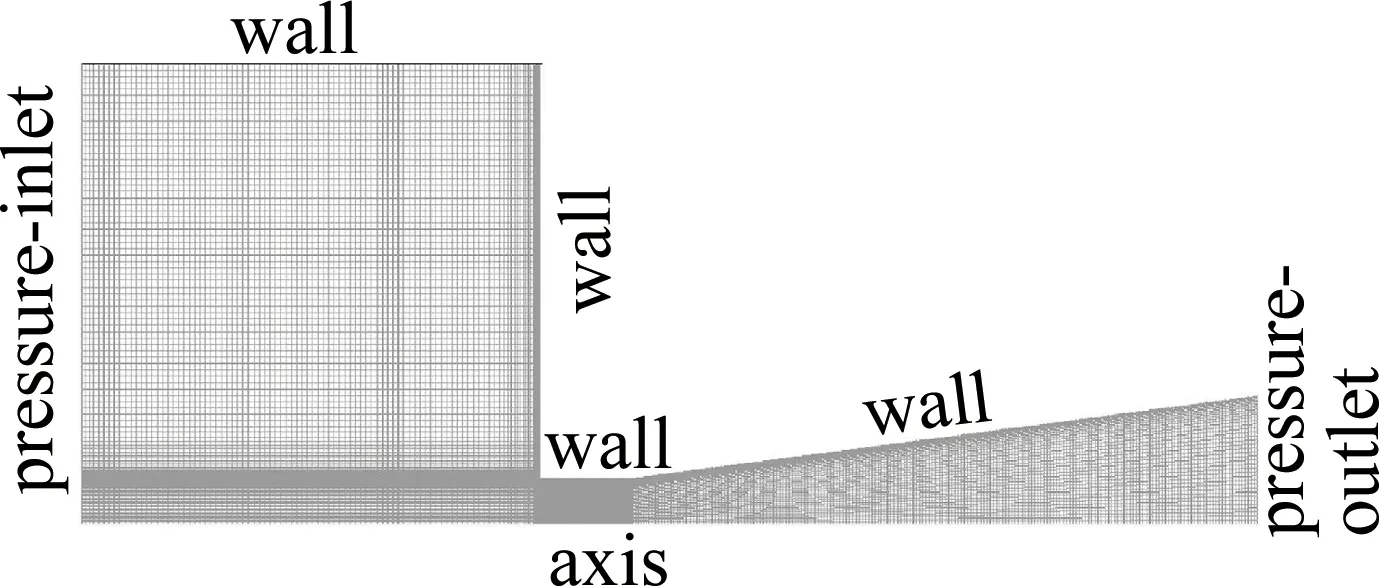
Fig.3 Gridding of calculation area
1.3 网格无关性验证
在考虑喷嘴几何形状和流速对射流形成的影响之前,确保模拟结果与网格无关即网格依赖程度可以忽略是至关重要的。因此,本研究中考虑了毛细管的3种不同的网格密度,并在雷诺数Re=5430下模拟了喷嘴内的射流流动。研究喷嘴的入口直径和毛细段长度均为0.128mm。毛细段轴向和径向网格密度分别为20×40,40×80和80×160。
图4为雷诺数Re=5430模拟计算660ns所得包含网格的水-空气两相图。从图中可知,网格密度越高,界面清晰度越好;但是流体相整体形状没有明显不同。因此为了减小运算时间,本文中采用中间网格密度40×80作为后续模拟计算。
2 模拟结果与分析
2.1 毛细带锥角喷嘴与锥状喷嘴对比
合格的水束光纤表面平滑准直,其内部的光线在水束与空气界面发生全发射,保证高效的光线传输效率[17]。水光耦合腔体内的水流经过充满空气的毛细段,与喷嘴内壁发生分离,主要原因是平面喷嘴上端的加压液流经过90°直角壁面时获得一定的动量,而这种动量促使流体在直角锐边发生明显的类抛物线运动。雷诺数Re=12800时,喷嘴毛细段水-空气两相随时间的模拟结果如图5所示。
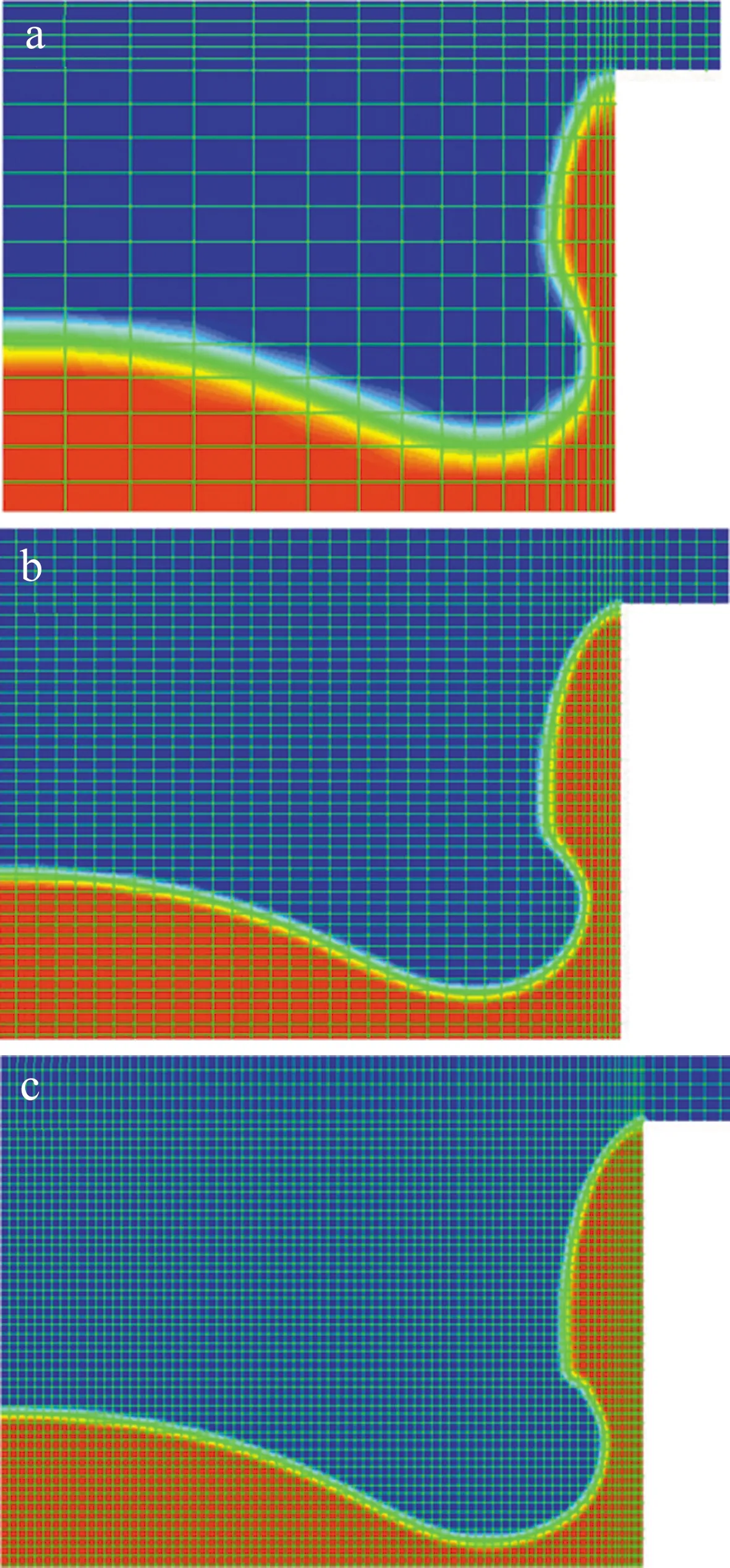
Fig.4 Axisymmetric simulation results of radial and axial densities of different capillary segments
液流经过直角锐边与壁面发生明显的分离,图5中t=2196ns的相图显示,水流前沿与壁面发生接触,产生再附壁现象。一旦流体再次贴近壁面,喷嘴壁面处会形成包裹空气的封闭循环区域,在此区域内空气泡会骤然破裂,随后水流充满整个区域。从图5中可以看到,明显的空气泡破裂以及其导致的水相离散,而这种空化现象对形成水束的稳定性和集束性造成强烈的扰动和湍动。喷嘴内部液流发生再附壁,形成的水束不再具备类层流和光滑特性。
锥角状喷嘴相比于毛细带锥角喷嘴,喷嘴入口直径为0.128mm,锥角为15°,雷诺数Re=12800时,喷嘴内部流体无再附壁现象发生,水束不受因接触壁面的扰动破裂的影响,两种喷嘴内部流场模拟结果对比如图6所示。
锥角状喷嘴内部射流由周围空气包裹,阻止其与壁面接触,壁面产生的湍流扰动无法作用于射流,准直光滑的水束生成。因此缩流现象对水束凝聚有重要的助益作用。

Fig.5 The phase diagram of the water flowing into the nozzle filled with air at different times at the Reynolds number of 12800
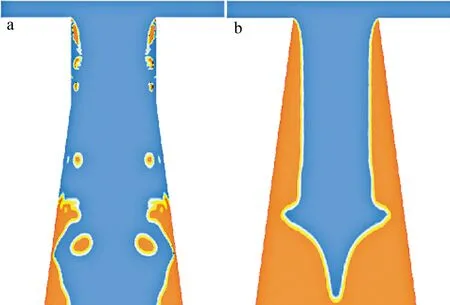
Fig.6 Water beam state under the same simulation conditionsa—capillary nozzle with cone angle b—cone angle nozzle
2.2 喷嘴入口不同雷诺数对再附壁长度作用
通过第2.1节中的模拟分析,可知喷嘴内部流体状态对水束特性有很大影响。水导激光工艺中水束的状态直接影响光束在类层流水光纤中的传输效率[18]。目前,国内外尚无关于喷嘴内部状态的定论,已有的经验模型依赖于修正实验数据所得。喷嘴内部流场状态可由空化数与临界返流数进行判断,其判断参量值主要由喷嘴长径比的比值,喷嘴上端倒角大小和入口直径的比值,以及入口雷诺数Re决定。本文中的模型为锐边入口,长径比为1的喷嘴,雷诺数Re对水束状态的影响作为主要研究目标,其经验公式如下式所示:
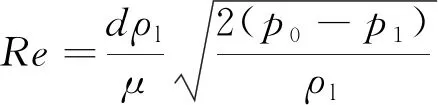
(4)
式中,d为喷嘴入口直径;ρl为液体密度;μ为流体的动力粘度;p0为喷嘴入口端压力;p1为喷嘴出口端压力。
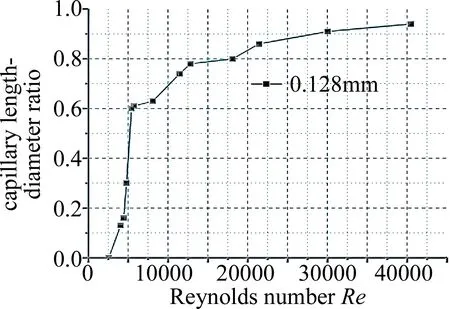
从前文可得,锥角状喷嘴相比于毛细带锥角状喷嘴更容易形成稳定水束。但是其锐边在高压入口的工作条件下易磨损,所以毛细带锥角状喷嘴具有更广泛的应用。鉴于此条件,对喷嘴毛细段水束再附壁长度进行探究。此模型下,水束再附壁位置主要与入口倒角和流体雷诺数有关,已知锐边入口,不同参量下的雷诺数大小可由(4)式计算可得。图7为喷嘴入口在不同压力下模拟所得再附壁长度。
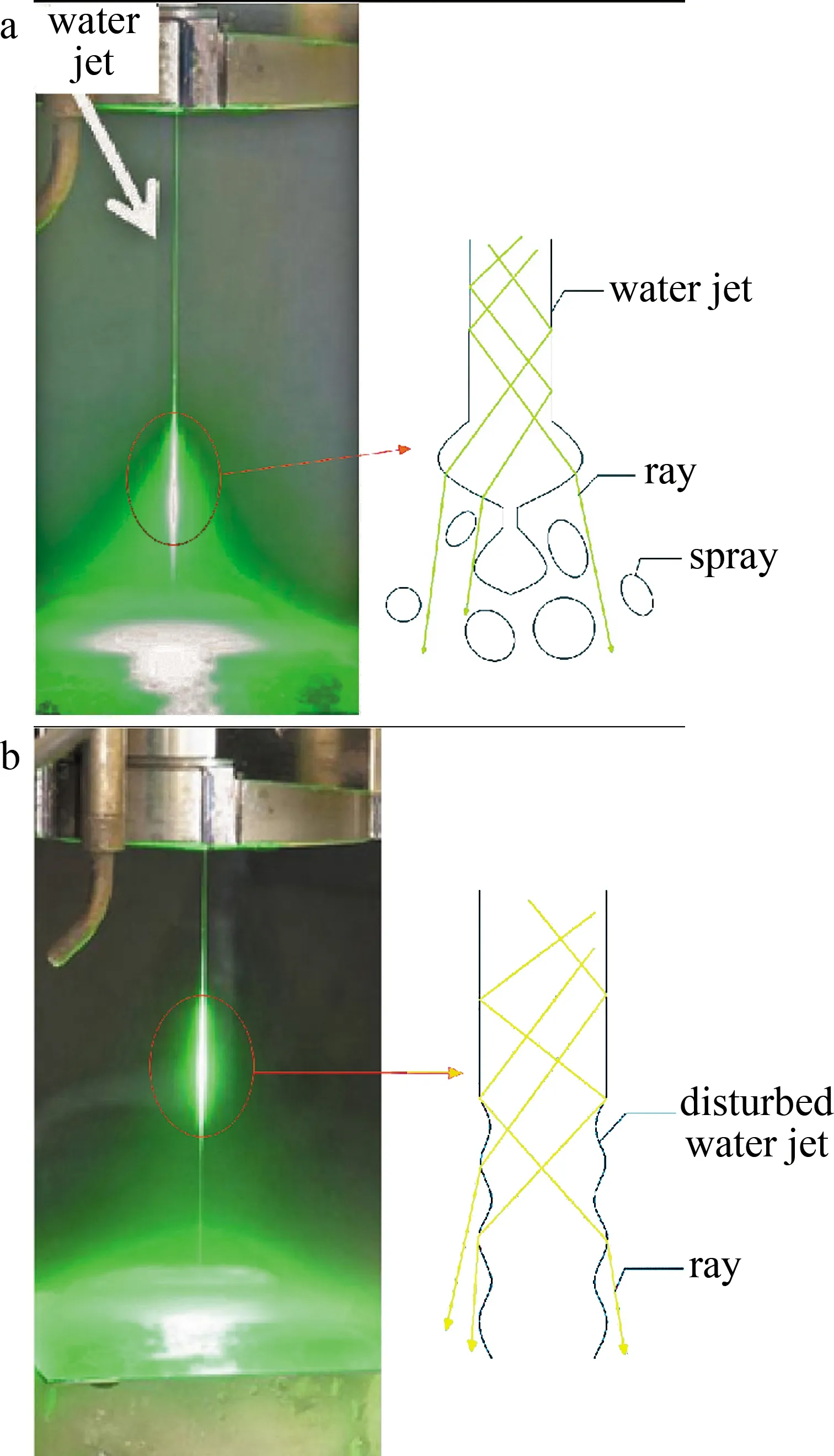
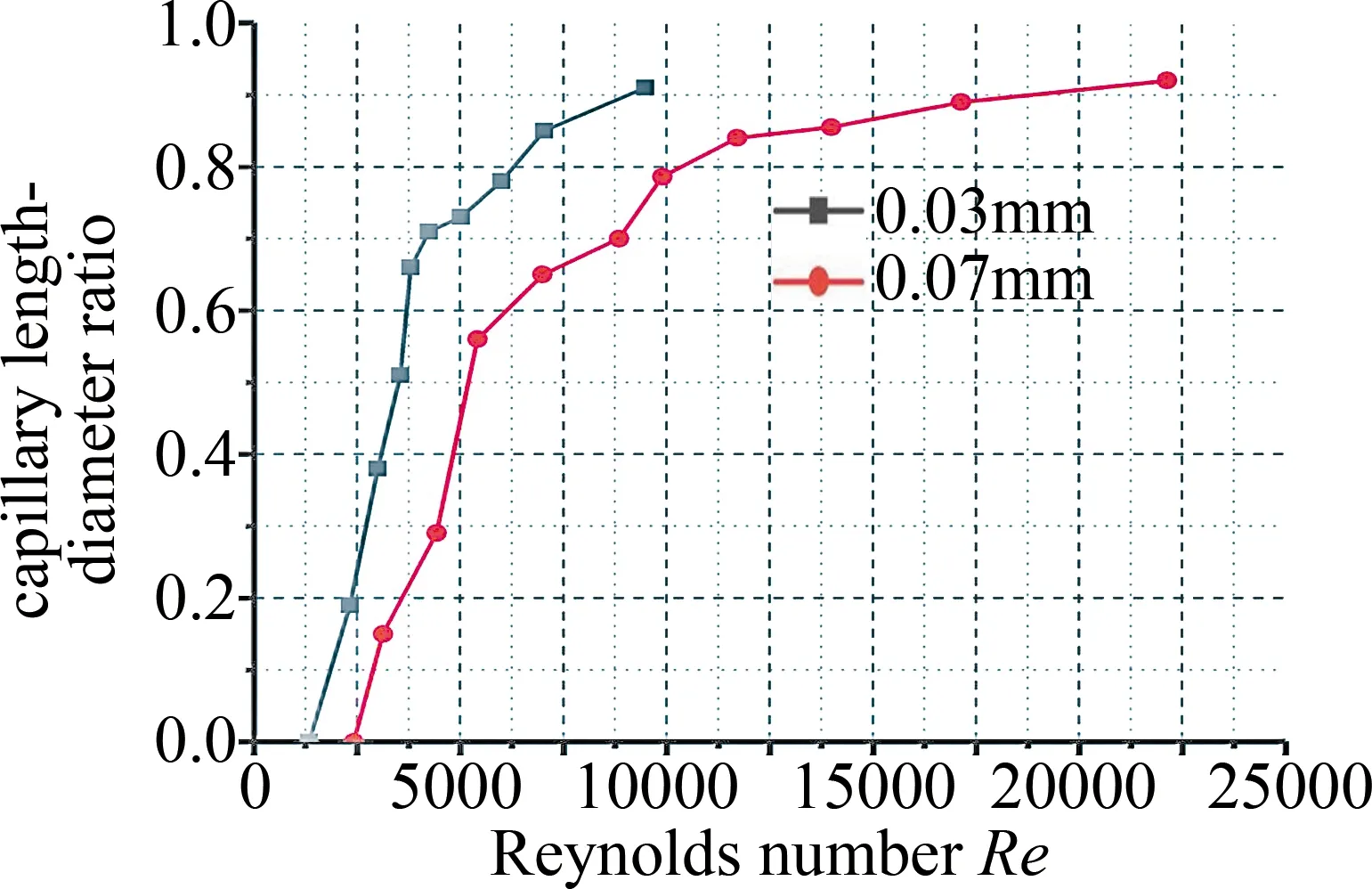
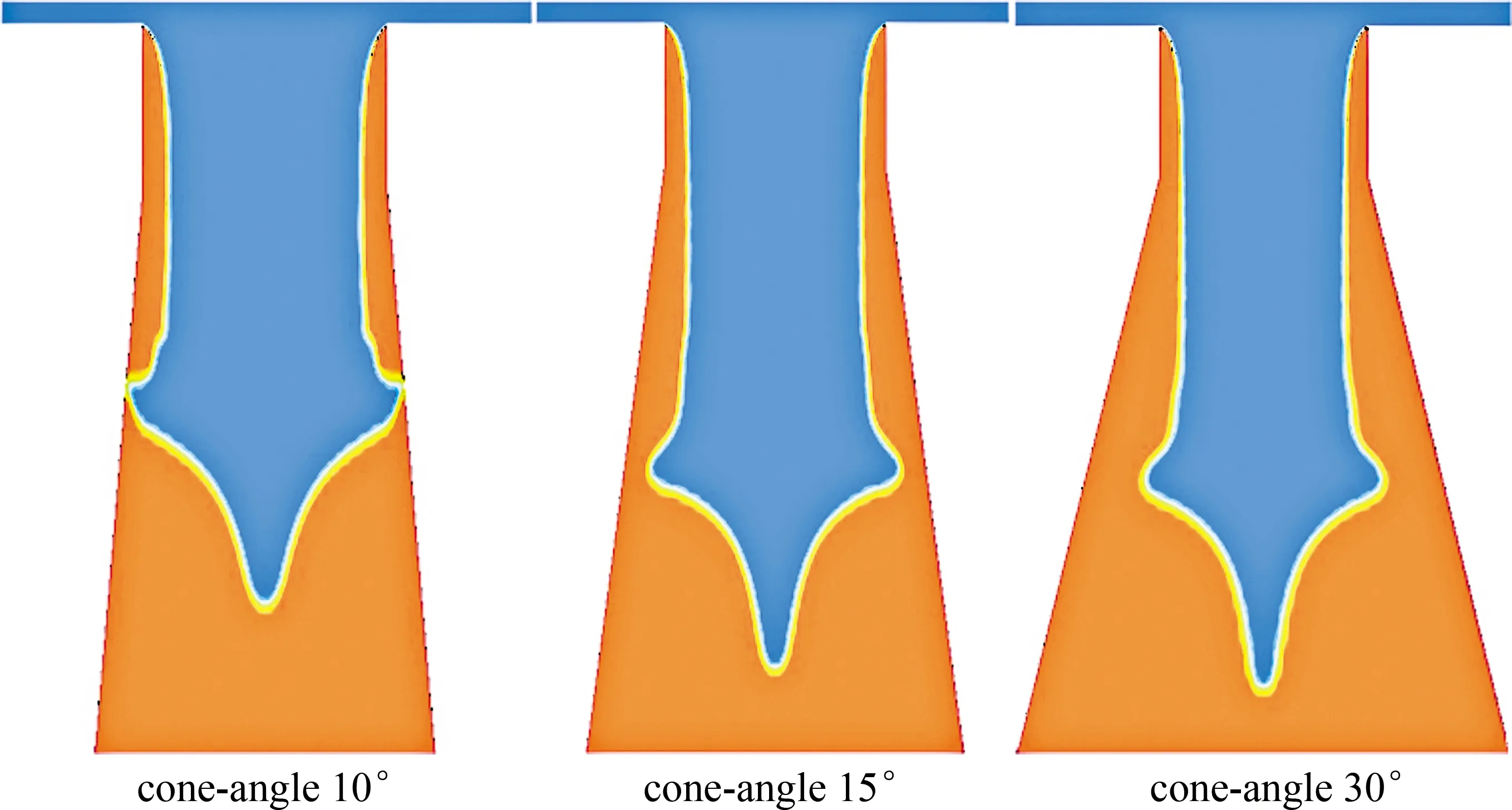
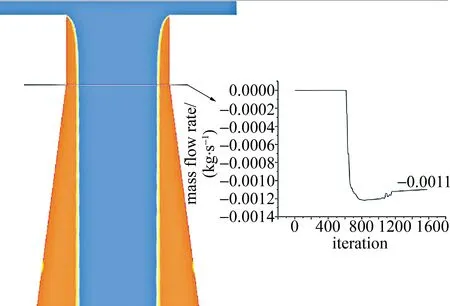
从图7中可得,低雷诺数下的水流因水平方向的动量不足以从毛细段垂直方向剥离,喷嘴内水相无明显分离现象。随着雷诺数增大(2560 Fig.7 Phase diagram of flow entering capillary nozzle with cone angle and reattaching wall at different Reynolds numbers Fig.8 The ratio of reattachment wall length to diameter under different Reynolds number of 0.128mm capillary section diameter 图8所示喷嘴毛细段再附壁长径比值随雷诺数增长呈递增趋势。当雷诺数Re=40000,喷嘴毛细段水流再附壁长径比值可达0.93。由(4)式可得喷嘴入口直径,内部流体密度,以及出口压力固定时,雷诺数Re的大小主要受喷嘴入口压力影响。从图8中可知,雷诺数Re=18100对应再附壁长径比为0.8。为检验其数值精度,取长径比为0.65,入口直径为0.128mm的毛细带锥角喷嘴,雷诺数Re=18100时,模拟结果如图9所示。 由图9可明显观察到,喷嘴内水流无再附壁现象发生。如果锐边喷嘴的毛细长度小于临界附壁长度,喷嘴结构对水束不稳定的影响可忽略,因此这时导致水束不稳定因素主要来自于整体供液结构的震动和流体脉冲[19],最终会导致已分离流体再次贴壁引起空化,水束破裂。针对水束状态对光线传导效率的影响问题,QIU等人[18]结合实验结果与图像处理算法的方式,并采用重构3维水束光纤模型,获得射流波动对光束的损耗特性,结果表明,处于波动段的射流,当其波动幅度和频率较小时,不足以引起光线传输损耗;当波动幅度过大时,无法满足水光纤特质,光线传输损耗急剧增加。CHIDA等人[20]研究辅助气体He对水束稳定性的影响,实验结果如图10所示。 Fig.9 No wall attachment in nozzle with aspect ratio of 0.65 at Reynolds number of 18100 Fig.10 Influence of assist gas flow rate on water-jet[20] 图10a为无辅助气体下激光在水束中传播的实验结果,可得水束存在稳定的工作距离范围,超出稳定范围的水束有剧烈的雾化现象,致使光线从水束逸散;图10b为流量5L/min的He辅助气体环境下,激光在水束中的传播状态。柱状水束表面受辅助气体影响出现非周期性波动,导致光线从水光纤中逸散,无法实现水导激光工艺。水束末端发生雾化,柱状表面出现局部波动都会导致光线从水光纤中逸散,所以光滑准直的稳定水束是水导激光工艺实现的前提。 通过对入口直径为0.128mm的喷嘴模拟分析,随着系统雷诺数逐渐增加,毛细段内的流体再附壁长度呈增长趋势。鉴于前面的模拟分析,分别对喷嘴入口直径为0.03mm和0.07mm水束再附壁长度进行探究,模拟所得数据对比如图11所示。 Fig.11 The ratio of reattachment length to diameter at different Reynolds numbers of 0.03mm and 0.07mm capillary segments 当喷嘴毛细段长径比值为1时,入口直径分别为0.03mm和0.07mm毛细段内部水束再附壁长度随系统雷诺数的增加而增加。系统雷诺数为0 从前面探究的结果可知,喷嘴入口的雷诺数对于水束状态有重要影响,决定水束再附壁的长径比值。本文中研究的平面喷嘴由毛细段和锥角段两部分组成。当喷嘴入口直径为0.128mm、雷诺数Re=18100、锥角为15°和30°时,模拟结果显示水束通过毛细段和锥角段均无附壁现象。当锥角为10°时水束在锥角段发生再附壁现象,如图12所示,进一步会发生空化导致水束雾化。 Fig.12 Water beam reattachment with different cone angle 综合模拟因素可知,喷嘴入口边缘的锐化,毛细段长径比值以及锥角段的角度对稳定水束的形成均有重要影响。当喷嘴边缘锐化呈直角状,入口雷诺数Re=18100,取毛细段长径比值小于0.8,且锥形段角度为15°,大于锥角段再附壁角度10°的条件下,喷嘴内部稳定水束生成,如图9所示。目前国内水导激光工艺处于实验室阶段,LI等人[17]通过激光粗加工,细丝研磨,锥形研磨头加工锥形槽,对喷嘴上表面进行研磨等工艺,最终获得适用于水导激光的锐边入口平面缩流型喷嘴。 正如前面已说明,在实验中证实微小毛细管内模拟数据的准确性十分困难。目前通过两个参量可验证模拟结果,流量系数Cd和缩流系数Cc。流量系数Cd定义为实验获得喷嘴的流率与伯努利方程理想状态下流率的比值。缩流系数Cc为通过喷嘴水束横截面积与喷嘴内部横截面积之比。喷嘴入口直径为0.128mm、雷诺数Re=18100时,取毛细段长径比L/D=0.65的位置,如图13所示。监测其质量流量率随运算迭代次数趋于稳定值0.0011kg/s。 Fig.13 Simulated extraction of mass flow rate data with L/D ratio of 0.65 Cd相对于模拟的流量系数则是黏性流体模拟所得质量流量率与非黏性流体理论所得质量流量率的比值,如下式所示: (5) Cd=0.0011/[π×6.42×1×10-10× (6) 同理,监测毛细段长径比值为0.65位置的相图尺寸数据图如图14所示。 Fig.14 Simulated two-phase size extraction data graph 水相占比50%的位置可得水相半径长度为5.05×10-5mm,缩流系数Cc的数值计算: (7) 式中,Ajet为水束的截面积,djet为缩流型水束的直径,d为喷嘴入口直径。根据模拟监测计算缩流无附壁水束状态所得流量系数Cd=0.61,缩流系数Cc=0.62。模拟监测计算所得两个数值和参考文献[21]~参考文献[23]中的实验数据有很好的一致性。 主要针对适用于水导激光工艺的平面毛细带锥角喷嘴内部水束状态,喷嘴几何参量以及系统雷诺数对缩流型水束形成的影响进行探究。 (1)模拟计算显示,当系统的雷诺数较小时,毛细段内水束再附壁长度比值随雷诺数增加而急剧增加,之后雷诺数继续增加,再附壁长度比值增加缓慢,当喷嘴入压力为50MPa,入口直径0.128mm,0.07mm和0.03mm喷嘴毛细段再附壁长度比值均可达0.9。 (2)模拟分析也表明,水束经过毛细段无附壁现象发生,但锥角段的角度减小到10°时,水束在锥角段发生再次附壁现象,因此喷嘴选取不同几何参量时其缩流水束形成参量也不相同。 (3)入口直径为0.128mm的喷嘴内流场模拟结果系数与已有实验测得数据具有很好的一致性。 通过对平面喷嘴内部流场的模拟计算,获得喷嘴几何参量以及入口水压(0MPa~50MPa)条件下光滑、稳定及准直的水束生成的关键因素。当喷嘴入口为锐边时,导引激光的稳定水束生成的前提条件是内部水束无再附壁现象发生。该研究为水导激光工艺中高压条件下的光滑稳定的微细缩流水束生成提供有效的数据参考。
2.3 锥角不同对水束再附壁影响
2.4 流量系数和缩流系数模拟结果验证
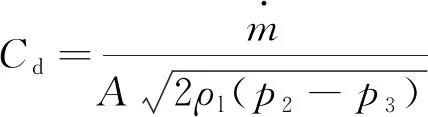
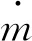
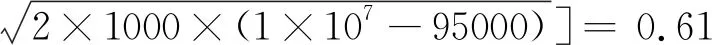

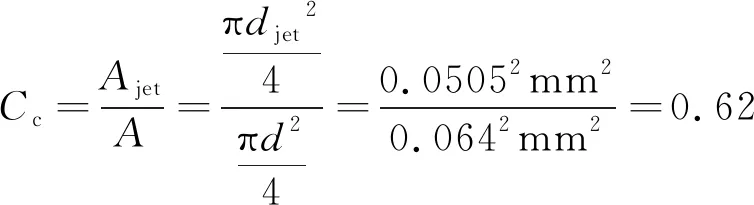
3 结 论
