基于适合分析T样条的曲面重构方法*
2020-11-11彭立华
鹿 昱,王 健,彭立华,徐 龙
(1.华中科技大学机械科学与工程学院,武汉430074;2.广州中旺龙腾软件股份有限公司武汉分公司,武汉430000)
曲面重构是指从一组离散的扫描数据点逆向推导出该物体的数学表达模型,这在很多领域是非常重要的,如航空零件、曲面测量、模具的制造与设计、3D打印、文物复原等。样条模型是曲面的常用表达方式,如B样条与NURBS,仅需一个控制网格和相应的控制顶点,便能表示任意的复杂曲面,广泛应用于CAD 等领域。此外,NURBS 还是曲面表达的标准格式。因此,以往的曲面重构算法都将点云数据拟合成B样条曲面或NURBS曲面[1–3]。但B样条与NURBS样条要求控制网格为规则的拓扑矩形,节点向量是全局共享的,难以实现局部细化,每引入一个节点,都需成行成列地加入新节点来满足拓扑要求,但这些节点对于曲面的控制完全没有意义。因此,B样条和NURBS曲面在表达特征信息丰富的复杂曲面时将产生很多冗余节点,这极大程度地影响了曲面设计及曲面重构的计算和存储。为解决这个问题,Sederberg 等[4–5]在2003年提出了T样条,并在2004年完善了该理论。与传统的B样条和NURBS 不同,T样条允许控制网格中存在T型节点,这使得T样条可以实现局部细化,每引入一个节点,只需引入若干节点,而不必为了满足拓扑要求成行成列地加入节点,极大简化了曲面的表达,节省了存储空间。
T样条提出后,很多学者利用T样条实现了曲面重构。Zheng 等[6]利用T样条完成了对z-map型数据的曲面重构;Yang 等[7]实现了对按行分布的数据点重构出连续的T样条曲面;Wang 等[8]根据曲率信息对引导误差分配,完成了对一般3D点云数据的曲面重构;Lin等[9]利用迭代的方法,优化了对大量点云数据的T样条曲面重构过程;Feng 等[10]提出了一种split-connectfit的思路,再一次提高了对大规模点云的T样条曲面重构过程。
T样条打破了B样条与NURBS的拓扑要求,实现了局部细化,但也带来了一些问题,如混合函数的线性独立性不能保证[5],这使得曲面重构方程的最小二乘解不唯一;再如T样条的混合函数的单位分解性不能保证[5],这使得一般的T样条曲面表达式均为有理式形式,不方便后续计算,若想得到简单的多项式形式,需要T样条为标准或准标准型[4–5],这就要求曲面重构时初始的T网格必须是标准或准标准的,一般只能选用B网格(如文献[6,8,9]中的方法),而不能输入点云的特征来分配节点;还有就是T样条的局部细化算法在某些情况下效果较差[11],不够稳定。这些问题不仅影响了曲面重构的过程,也给曲面设计、等几何分析等领域的应用造成了很大困难。
为了解决这些问题,Li 等[12]提出了AST样条。AST样条是T样条的一个子类,是有一定拓扑限制的T网格。AST样条的混合函数具有线性无关性,且附加一些简单的额外条件后,混合函数也具有单位分解性[13]。之后,Scott 等[11]给出了AST样条的局部细化算法,该算法比一般T样条的局部细化算法更加稳定。AST样条自从提出以后,便被迅速应用到了等几何分析领域[14–15],但曲面重构领域还基本只有使用T样条的方法。因此,本文提出了利用AST样条实现了3D点云数据的自适应曲面重构算法。
1 AST样条
1.1 T样条
与B样条和NURBS 类似,T样条也是定义在一个由节点(图1中的黑点)和边(图1中的实线)组成的控制网格及其相应控制顶点上的样条,而这个控制网格,就叫做T网格。与B样条和NURBS样条的控制网格不同,T网格中允许存在T节点,如图1所示,其中的P1、P2这两个节点就叫做T节点。
三维空间中的控制顶点与T网格中的节点一一对应。给定了T网格和对应的控制顶点后,T样条的具体表达式可以写为:

其中,wi是权值;Pi是控制顶点,而Bi(u,v)是每个节点的混合函数,具体形式为:

其中,N[ui](u)和N[vi](v)是分别定义在如下两个节点区间上的3次B样条基函数:

给定一个T网格,每个节点的节点区间ui和vi按文献[4]中的方法决定。在T网格中,设该节点的坐标为(ui2,vi2),以该点作为原点,向右(u增大的方向)发射一条射线,与该射线最先相交的两条边的坐标,即为ui3和vi3。其余的坐标可按类似的方法得出。图1给出了具体的例子,节点P1的节点区间已用红色方框标出。
1.2 AST样条

图1 带有两个T节点的T网格Fig.1 A T-mesh with two T-junctions
AST样条是T样条的一个子类,需要附加一些拓扑上的限制,而这些限制建立在T节点扩展的概念上。对于每个T节点,设这个T节点的节点区间为式(3)所示,则该T节点扩展是指这样一条线段:若该节点缺失右边,则该点的T节点扩展为线段若该节点缺失左边,则该点的T节点扩展为线段若该节点缺失上边,则该点的T节点扩展为线段若该节点缺失下边,则该点的T节点扩展为线段
对于一个给定的T网格,如果其水平方向的T节点扩展与竖直方向的T节点扩展两两不相交,则该T网格为AST网格;相应的,定义在这个AST网格上的T样条曲面就叫做AST样条曲面。图1中的T网格就是一个AST网格,其中两个T型节点的T节点扩展已用蓝色矩形标出。
2 自适应AST样条曲面重构
给定一组3D数据点V和一个误差阈值ε,AST样条曲面重构可以描述为:寻找一个AST样条曲面S(u,v),使得以下不等式成立:
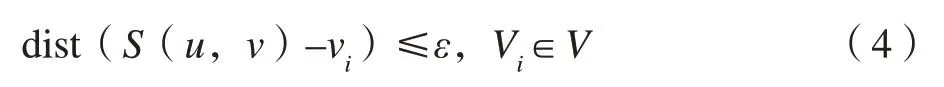
在本文的算法中,实现以上目标主要包含以下几个步骤:对输入数据V进行参数化并得到参数结果U,再根据U构建初始的T网格并将其转化为AST网格,之后利用最小二乘法求解控制顶点,得到AST 曲面并计算误差,在误差不满足阈值ε的要求处进行AST网格的局部细化,直至满足误差要求。图2给出了算法的程序流程图。
2.1 参数化
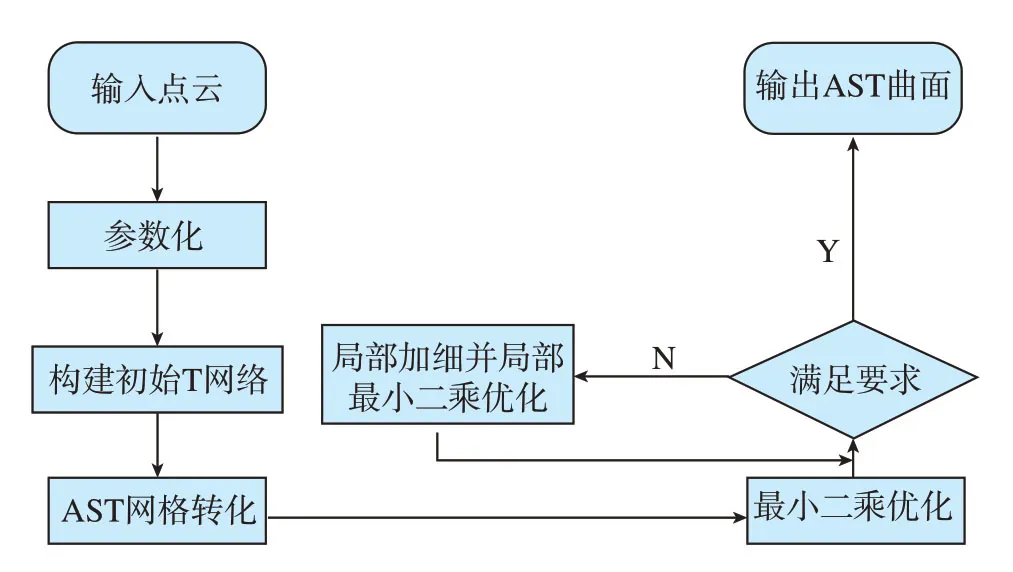
图2 自适应AST曲面重构算法流程图Fig.2 Flow chart of ASTS reconstruction algorithm
三角网格的参数化是一个3D数据到2D数据的映射G:对于给定的三角网格T 中的任一个数据点Vi=(xi,yi,zi)∈R3,都有一个Ui=(ui,vi)∈R2与之对应,即Ui=G(Vi)。三角网格的参数化是参数曲面重构的重要步骤。得到结果后,便可根据参数化结果U构建AST网格,进而计算后续的计算。对于z-map型数据[16],由于其x与y坐标成阵列形式,不会出现重复,因此可以直接将其x坐标与y坐标作为参数化结果;对于一般的3D数据,本文使用了长方形边界参数化[17]。长方形边界参数化使得参数结果分布在规整的长方形区域内,有利于根据参数点来构建初始T网格。该算法的详细步骤可参阅文献[17]。
2.2 初始T网格的构建
得到点云数据的参数化结果后,便可以构建初始的T网格。在很多现有的算法中[6,8,9],为了保证混合函数的线性独立性与单位分解性,初始的T网格被设定成一个n×n的标准T网格(图3(a)),后续网格的细化完全依靠误差引导的网格细分。根据误差细分网格是一个必不可少的步骤,但这一步骤的计算耗时较久,如果能根据点云几何信息构建一个良好的初始T网格,则会大大减少根据误差细分网格的步骤,减少计算时间。但这样做就难以保证该T网格是标准的,因此在现有的基于一般T样条的重构算法中,难以实现。然而AST样条并没有这种限制。因此,本文提出了一种依据T网格中每个最小长方形内所包含的参数点个数及特征点个数来构建初始T网格的方法(图3(b))。
2.2.1 特征点的计算
特征点的选取有很多种方法,一种常见且有效的方法便是依据曲率进行选取。在本文的方法中,也采用曲率作为评价标准,将曲率较大的点作为特征点。对于连续光滑平面上的一个点,其曲率有无穷多个,其中最大的曲率记为k1,最小的曲率记为k2,这两个曲率叫做主曲率,而高斯曲率k可表示为这两个曲率的乘积。高斯曲率表示了该点曲率的综合性质,高斯曲率较大的点,曲面弯曲程度大,视为特征点。本文的处理对象是离散的三角网格,两个主曲率的计算是利用文献[18]中的方法。主曲率得到后相乘便可以得到每个数据点的高斯曲率,选取高斯曲率值较大的数据点作为特征点,在本文的计算中,选取的比例设定为10%。

图3 现有算法中常用的m×n初始T网格与本文提出的自适应构建的初始T网格(星标为特征点)Fig.3 m×n initial T-mesh grid used in most existing algorithms and proposed adaptively constructed initial T-mesh (feature points are marked withstars)
2.2.2 网格的自适应细分
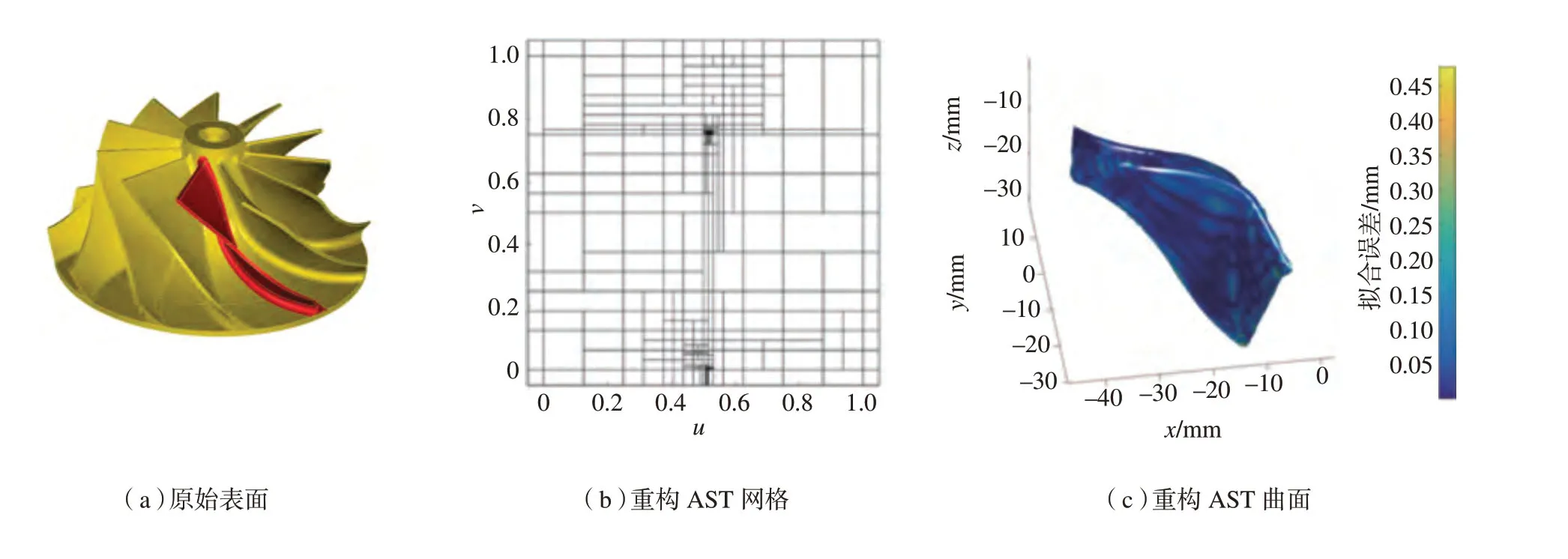
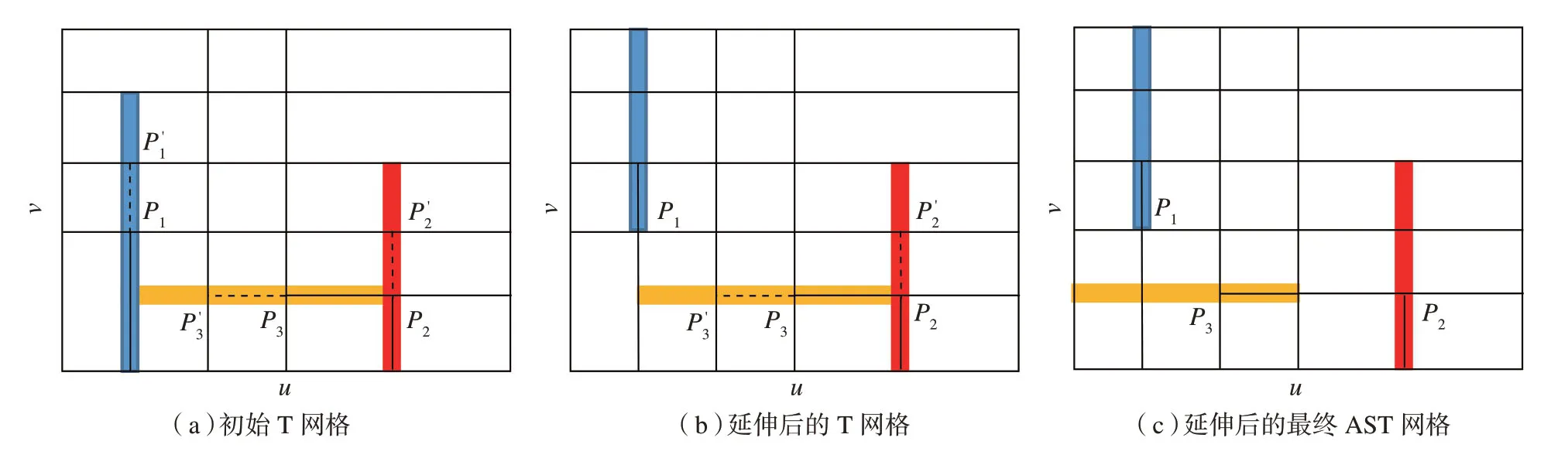
根据参数化的结果,所有的数据点均分布在[0,1]区间内。因此,选取一个[0,1]×[0,1]的正方形网格作为最初始网格来进行细化。网格的细化是依据最小长方形中的参数点数量以及特征点数量来进行的。给定一个参数点数量的阈值Nd和特征点数量阈值Nf,当一个最小长方形中的参数点数量超过Nd或者特征点数量超过Nf时,就将其一分为二,直至满足阈值要求。划分时在长方形的长边进行划分。也就是说,设该长方形的左下角节点的坐标为(umin,vmin),右上角节点的坐标为(umax,vmax),如果umax–umin 2.2.3 构建缩减参数域 图4 扩展后的最终初始T网格(灰色区域为缩减参数域)Fig.4 A complete initial T-mesh with extended boundaries (reduced parametric domain is marked in grey) 文献[13]指出,AST样条曲面的混合函数在缩减参数域上具有单位分解性,如图4所示,灰色区域即为缩减参数域。因此,上一步得到的网格需要扩展一层来保证点云的参数值均处于缩减参数域内。如图4所示,将网格边界上的所有节点向外扩展一个距离为的新节点,并连接,形成一个新的[–μ,1+μ]×[–μ,1+μ]的网格,而原来的[0,1]×[0,1]的正方形网格部分变为缩减参数域。 AST网格转化算法是整个算法中的重要步骤,在初始T网格构建完成后,一般来讲这时的T网格只是一般T网格,而不满足AST网格的要求,需要将T网格转化成AST网格;另外,在后文中的每一步局部细化中,每一次的网格加细产生的中间T网格往往也都不是AST网格,需要将其转化成AST网格。 正如前面所介绍的,AST网格是T网格的一个子类,只有当一个T网格中所有的水平T节点扩展和所有的竖直T节点扩展均不相交时,这个T网格才叫做AST网格。一个一般的T网格可以转化成很多个AST网格,但我们需要找到那个最简单的网格,或者说,最接近原网格的AST网格,即转化所插入的节点数量最少。这是一个NP-hard 问题[11],采用与文献[11]中类似的方法,用贪婪策略来寻求局部最优解。具体的方法为: (1)找到原T网格中所有相交的T节点扩展及其相应的T节点。 (2)对上一步骤中的每一个T节点,沿其缺失的方向进行一次延伸,得到一个新的T网格,并计算新的T网格中相交的T节点扩展的个数。对每个T节点都如此做,找到相交的T节点扩展的个数最小的那个T网格替代之前的T网格。 (3)重复步骤(2)直至没有相交的T节点扩展,得到最终的AST网格。 图5 AST网格转化算法示例Fig.5 An example of AST-mesh conversion 该算法是一定有解的,不会出现相交的T节点扩展越来越多的情况,因为最差也会得到一张B网格结构。图5给出了一个例子。P1、P2和P3是T网格中的3个T节点,其中,P1与P3、P2与P3的T节点扩展(已用蓝、红、黄三色长方形标出)相交,因此该T网格不是AST网格。依次对这3个T节点按图中虚线方向进行延伸,如图5(a)所示,延伸P2并不会改变T节点扩展的相交情况,但延伸P1或P3之后,只剩1组相交的T节点扩展,因此,这一步选择延伸P1(选择P3也可以)得到图5(b);此时只剩下P2与P3的T节点扩展相交,延伸P2不会改变相交情况,但延伸P3后便不存在相交的T节点扩展,因此,这一步选择延伸P3得到图5(c)的T网格,该网格的所有T节点扩展互不相交,便是最终的AST网格。 给定一个AST网格,并令所有节点的权值w为1,利用AST网格的单位分解性,式(1)可写成如下形式: 给定一组m个数据点的3D点云数据V及其参数化结果U,我们希望找到一组控制顶点P,使得该AST样条曲面与点云数据V在最小二乘意义下距离最小,即: 如果将控制顶点P和数据点V写成列向量,则该优化问题可化为求解超定方程组AP=V的最小二乘解,其中,Ai,j=Bi(uj,vj)。根据AST样条混合函数的线性无关性,该方程的最小二乘解P*是唯一的,即: 控制顶点P确定后,整个AST样条曲面就被完全确定,所有数据点的误差E也可由下式计算: 得到每个点的误差后,便可以根据误差的大小来进行局部细化,使得所有数据点处的误差均能满足误差要求。具体的做法会在下一节讨论。 当拟合出一个AST样条曲面时,如果一个数据点的误差值大于给定的允许误差,那么就要将该点所在的最小长方形一分为二,划分方法与2.2.2 节中所提到的划分方法一样,沿长边进行划分。在划分完成后,新生成的T网格往往不是AST网格,需要用2.3 节中所介绍的AST网格转化算法将其转化成AST网格,才能作为细化后的结果。细化会引入新的节点与边,根据AST样条的定义,其周围的一些节点的节点区间也会因此发生变化。再由AST样条基函数的局部支撑性质可知,这些节点区间发生变化的节点只在其区间内非零,也就是说,只有定义在这些区间的曲面会受到影响,而其他位置处的曲面均不受影响。因此,可以找到受影响区域内的数据点作为拟合对象,新加入的节点和节点区间发生变化的节点的控制顶点一起作为未知量求解,而其他的控制顶点作为已知量[19]。求解方法和2.4 节所述相同,采用最小二乘法求解,区别在于输入数据和未知量不同。 假设输入数据有m个,细化后的AST网格含有n个节点,其中,新引入的节点和节点区间改变的节点共计r个,这r个节点的混合函数在s个数据点上非零。细化后,只需用这s个数据点作为拟合数据,上述的r个节点的控制顶点作为未知量,而其余节点的控制顶点作为已知量。取混合函数矩阵A对应的s行,并根据对应的r列写成分块矩阵,则待求解的方程组可表示为: 其中,Pr是待求未知量,将方程移项,则方程的最小二乘解Pr*可用下式快速计算: 求得控制顶点后,重新计算误差,并不断重复上述步骤,直至误差满足要求,便可得到重构出的AST样条曲面。 本文针对仿真数据及真实数据均进行试验,试验平台为Matlab。其中真实数据是来自LaserDesign数据库的涡轮叶片数据[20]。作为对比,NURBS 方法(类似文献[21])与T样条方法(类似文献[6,8])也被用于同样数据的曲面重构。 仿真数据为二元函数,具体表达式为: 在[–8,8]×[–8,8]的范围上生成一个161×161,共计25921个点的Z–map点云集,先用本文提出的AST样条曲面重构算法对该数据进行拟合。拟合的误差阈值设置为0.02。第1步生成的AST样条曲面拟合的最大误差为0.017,平均误差为0.005,已经满足误差要求。整个拟合过程耗时3s。最终的AST样条曲面共有85个控制顶点,图6给出了原始曲面、重构AST网格和曲面。 作为对比试验,针对同样的点云数据,用控制顶点数量相近的均匀节点NURBS曲面来拟合该点云数据。重构出的NURBS曲面具有9×9=81个控制顶点,与AST 曲面相近,但最大误差为0.261,平均误差为0.064。与此同时,基于T样条的拟合方法也同样用于拟合该数据来对比同样参数条件下的计算效率。经过13次加细后得出了最终T样条曲面,共计耗时25s。 实际数据采用了涡轮叶片数据,共计16854个数据点。与上节相同,先用本文提出的AST样条曲面重构算法对该数据进行拟合。拟合的误差阈值设置为0.5mm。经过17次加细后满足误差得出最终重构曲面,最大误差降为0.477mm,平均误差降为0.058mm。最终的AST样条曲面共有493个控制顶点,计算用时136s。图7给出了该案例原始曲面、重构AST网格及曲面。 作为对比试验,针对同样的点云数据,用控制顶点数量相近的NURBS曲面来拟合该点云数据。重构出的NURBS曲面共有22×22=484个控制顶点,与AST样条曲面的493个控制顶点相近,但重构的最大误差为3.156mm,平均误差为0.232mm。与此同时,基于T样条的拟合方法也同样用于拟合该数据来对比同样参数条件下的计算效率。经过24次加细后得出了最终T样条曲面,共计耗时220s。 从试验结果可以看出,对于同一组数据,在控制顶点数量大致相同时,本文提出的AST样条重构方法比传统B样条与NURBS 方法重构出的曲面精度更高;与现有的基于T样条重构算法相比,具有更高的计算效率。 本文提出了一种基于AST样条的3D点云数据自适应曲面重构算法。根据输入点云的曲率信息构建初始T网格并AST 化得到初始的AST网格,利用最小二乘法求解控制顶点,得到AST样条曲面,并根据误差不断细化AST网格,直至满足误差要求。试验表明,对同一点云数据,与NURBS 重构出的曲面相比,在控制点数量大致相同时,利用AST样条重构出的曲面精度更高;与现存的T样条重构方法相比,本文提出的基于AST样条的算法具有更高的计算效率。 图6 仿真数据曲面重构实例Fig.6 Surface reconstruction for artificial data 图7 涡轮叶片曲面重构实例Fig.7 Surface reconstruction for an impeller blade
2.3 AST网格转化
2.4 最小二乘法计算控制顶点




2.5 AST网格局部细化与局部最小二乘优化

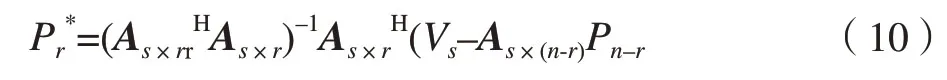
3 试验
3.1 仿真数据
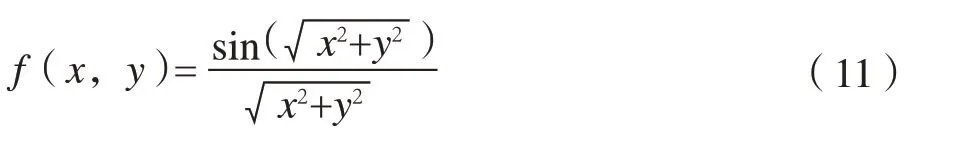
3.2 实际数据
4 结论