基于多目标优化的微铣削表面粗糙度检测指标研究

2020-11-11

航空制造技术 2020年19期

（长春理工大学跨尺度微纳制造教育部重点实验室，长春130022）

微铣削加工技术是微制造业的一种先进制造技术，具有可加工三维微小复杂零件的优势，广泛应用于航空航天领域中[1–2]。相较于常规铣削，微铣削对表面质量的要求更加严格，因刀具和工件尺寸缩小及切削厚度减小引起的尺寸效应，表面质量更难控制。因此，微铣削条件下对加工表面形貌进行准确地检测具有重要意义。

表面粗糙度是加工表面质量检测的重要衡量指标，直接影响零件的工作精度、耐腐蚀性和耐磨性等[3]。近年来，国内外学者对微铣削表面粗糙度的评价和优化进行了大量研究。高奇等[4]设计了正交试验对单晶高温合金的微铣削表面粗糙度进行研究，基于极差分析得到工艺参数对表面粗糙度Ra的影响主次因素，并获得工艺参数的优化组合，实现表面粗糙度优化。Kuram 等[5]针对Ti6Al4V 合金和Inconel 718 两种材料，采用田口试验设计方法确定了表面粗糙度的最佳微铣削条件，优化了表面粗糙度。但由于在微铣削的实际加工过程中工艺参数对表面形貌的影响不同，导致表面出现异常特征，从而使加工表面高度呈现非高斯分布。因此，使用单一的参数对表面粗糙度进行检测不够准确，选择多个合适的参数能够使检测更为全面。目前常见的多为粗糙度与其他加工因素的多目标优化，以实现响应目标的优化。Lu 等[6]利用田口法和回归分析在Inconel 718 微铣削过程中基于遗传算法获得了最大材料去除率和最小表面粗糙度多目标优化的最佳切削参数。Thepsonthi 等[7]利用有限元分析和数学建模，基于多目标粒子群优化方法寻找Ti–6Al–4V合金微端铣削刀具路径和工艺参数的最优解，实现表面粗糙度的优化。Beruvides 等[8]利用微铣削过程中产生的振动信号预测表面粗糙度，采用自适应神经模糊推理系统模型对表面粗糙度进行建模，使用多目标遗传算法针对单位加工时间和粗糙度进行了多目标优化。

二维表面粗糙度广泛地用于科学分析和工程实践中，但已经不能满足技术发展对表面形貌信息检测的需求。表面粗糙度的表征逐渐由二维向三维发展，轮廓算数平均偏差Sa、表面偏斜度Ssk和表面峭度Sku分别为Ra、Rsk和Rku在三维的扩展，其中Sa具有望小特性，即Sa越小表面质量越好，而表面偏斜Ssk和Sku具有望目特性，即当Ssk为0、Sku为3时为高斯表面，表面无异常特征。本文以Sa、Ssk和Sku为研究对象，基于灰色关联分析法和响应曲面法（Response surface methodology，RSM）将多目标参量转化为灰色关联度（Grey correlational grade，GRG）作为表面粗糙度检测指标，分析了微铣削过程中的主要工艺参数对灰色关联度的影响规律，构建灰色关联度模型，对工艺参数进行了优化，对检测指标进行验证。

试验及方法

1 试验设备及材料

试验在Mikron MILL P 900高性能加工中心进行，微铣削加工的材料为常用于航空航天工业的7075 铝合金，工件体积参数为16mm×16mm×20mm。为了避免刀具磨损的影响，每组试验均使用全新的刀具，刀具选用直径为1mm的双刃硬质合金端铣刀，螺旋角为30°，切削方式为干切削。微铣削加工过程如图1所示。

三维表面粗糙度的确定使用法国STIL 光谱共焦显微镜，量程为130μm，横向分辨率为0.1μm，纵向分辨率为35nm。

2 试验方案

响应曲面法涉及数学方法和统计方法，用于试验的设计和分析，优化多变量响应[9–11]。Box-Behnken Design（BBD）方法是最常用的响应曲面优化法之一。本文选用了主要加工工艺参数即主轴转速n、进给速度vf、轴向切深ap和径向切深ae，根据BBD 法的要求设计了4 因素3 水平试验，试验水平分布见表1，试验参数安排及三维表面粗糙度见表2。

图2所示为表2中第2、1、4组试验的加工表面形貌，分别记为表面1、表面2、表面3。表面3相对于表面1和表面2其进给速度增大，即每齿进给量增加，比较图2可以明显看出表面3的刀具轨迹更为清晰，同时导致表面整体的微细毛刺较大，3个三维表面粗糙度参数显著增大。表面1相对于表面2和表面3其轴向切深增大，导致刀具颤振加剧，表面不规整的微细毛刺增多，从而使Sa、Ssk、Sku均增大，降低表面质量。表面1、表面2、表面3的径向切深依次增大，刀痕重叠率相应依次降低，残留高度相应增大，则Ssk减小而Sa和Sku增大。由于工艺参数对粗糙度影响大小不同以及耦合影响的作用，粗糙度变化规律复杂，检测难度增加。

图1 微铣削加工现场图Fig.1 Machining scene of micro-milling

表1 试验参数水平分布Table1 The level of experimental parameters

3 多目标优化方法

灰色关联分析是灰色系统理论的重要组成部分，通过分析因素之间的发展趋势来衡量因素间的关联程度，用于分析事物之间的不确定性关联[12]。基本思路为通过比较确定的参考数据序列和比较序列之间几何形状的相似程度，基于灰色关联度来描述两个因素之间的关联程度。多目标优化使用基于主成分分析的灰色关联分析方法，具体过程如下：

（1）记xi0(k)为第k个指标的第i个参数，其中i=1，2，…，m；k=1，2,…，n。由于因素的量纲不同或数量级相差较大，不便做比较或比较结果不准确，为了消除这种影响，对原始数据做标准化处理得到序列xi*(k)，其中具有望小特性和望目特性的因素分别按照式（1）和式（2）进行处理。

（2）选取每个粗糙度参数的理想值组成参考序列x0*(k)，标准化后的序列作为比较序列。

（3）灰色关联系数表征的是参考序列和比较序列的关联程度，根据式（3）计算灰色关联系数。

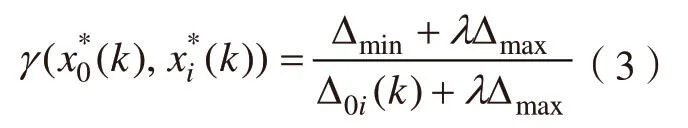
（4）主成分分析是一种非线性降维方法[13]，能够分析各个变量因素对响应目标的贡献率。对灰色关联系数进行主成分分析，通过主成分分析法量化分析粗糙度对灰色关联度的影响权重。

（5）灰色关联度是灰色关联系数的加权和，是综合评价的结果。根据式（4）计算灰色关联度：

式中，βk为第k个响应变量的权重，

结果与讨论

1 多目标优化结果

对表2中的试验数据进行前文中的多目标优化转换。经主成分分析得到粗糙度参数Sa、Ssk和Sku对灰色关联度的响应权重分别为0.479644045、0.296122676和0.224233279，根据响应权重将3个三维表面粗糙度参数进行加权和计算，转换为单一的表面粗糙度检测指标即GRG 以进行灰色关联度模型的建立，计算结果见表2。

2 灰色关联度模型建立

设计参数与目标响应之间的关系是RSM 通过回归分析方法得到的，通常采用二阶回归模型来表示。本文基于RSM建立了加工参数与灰色关联度之间的映射关系，灰色关联度模型见式（5）。

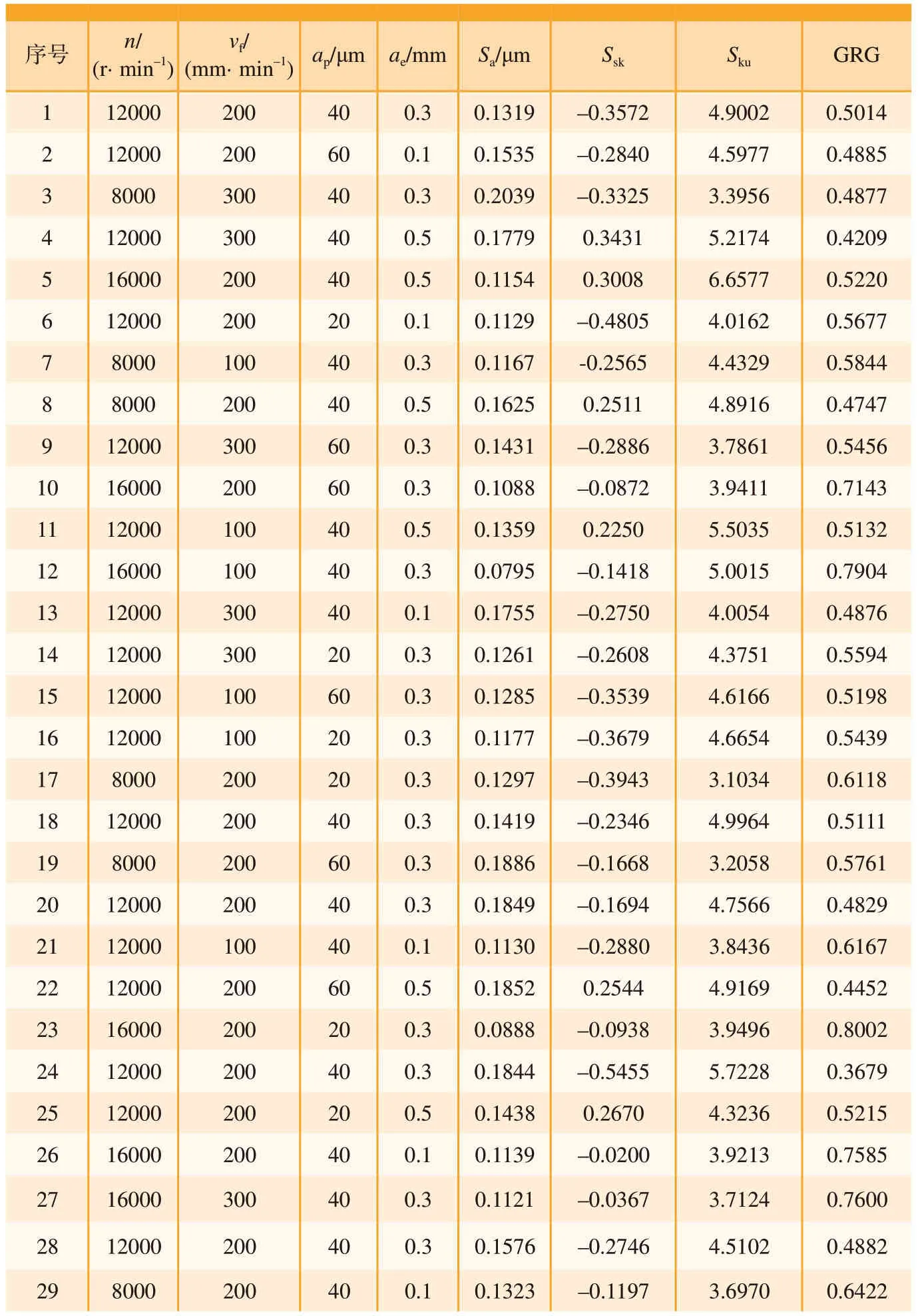
表2 试验参数安排及结果Table2 Arrangement of experimental parameters and results

图2 部分试验加工表面形貌Fig.2 Machined surface morphology of several experiments

方差分析可以检验回归模型的显著性及失拟情况，从而建立模型的拟合精度[14]。表3对基于RSM建立的灰色关联度模型进行了方差分析。P值表示信度，模型的P值小于0.05，而失拟项的P值大于0.05，即模型显著而其失拟项不显著，表明所建回归模型拟合较好，模型可靠。图3比较了实测计算值与模型预测值，平均相对误差为6.54%，拟合误差较小，精度较高；图4为拟合模型的残差概率分布图，所有残差点均在直线附近波动，无明显异常点。因此，基于RSM建立的回归模型可作为灰色关联度模型。

3 影响规律分析

主效应分析可以度量1个或多个因子在各水平上对响应的影响大小[15]。利用主效应分析研究微铣削工艺参数对GRG的影响，结果如图5所示，其中横轴为单因素的多水平，纵轴为响应即GRG 数值，水平实线表示响应平均值。

由图5可知，主轴转速和径向切深的变化幅度较大，表明主轴转速和径向切深对GRG的影响较大，而进给速度和轴向切深对GRG的影响相对较小。其中，GRG 随着进给速度、轴向切深和径向切深的增大均呈减小的趋势，因此，GRG 在高主轴转速、低进给速度、低轴向切深和低径向切深处更大，表面质量更优。除此之外，由表3的方差分析结果可知，主轴转速和径向进给的P值小于0.05，对灰色关联度的影响显著，而进给速度和轴向进给的P值大于0.05，对灰色关联度的影响不显著；F值用来评估组间差异，F值越大，工艺参数对灰色关联度影响越大，故工艺参数对灰色关联度的影响大小顺序为：主轴转速>径向进给>轴向进给>进给速度。

表3 GRG模型的方差分析Table3 Analysis of variance of GRG model

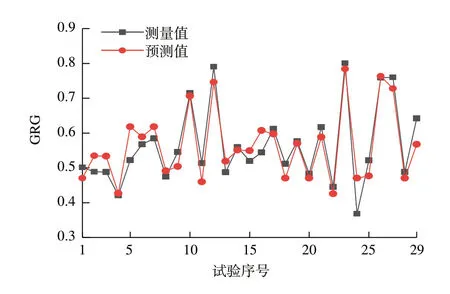
图3 实测计算值和模型预测值的比较Fig.3 Comparison of actual measured values and model predicted values

图4 模型的残差概率分布图Fig.4 Residual probability distribution of model

GRG模型进行方差分析后得到各工艺参数耦合因素的F值，如图6所示，可以直观地比较F值的大小，F值越大，耦合作用越显著，则工艺参数间耦合作用对灰色关联度的影响大小顺序为：n–ae>n–vf>n–ap>vf–

由于进给速度对GRG的影响最小，固定进给速度作为第四维绘制GRG与微铣削工艺参数相关的响应轮廓如图7所示。

观察图7可知，由于进给速度对GRG的影响相较于本文其他工艺参数较小，当进给速度取不同水平时，响应轮廓呈现出相似的变化趋势。当主轴转速与轴向切深耦合作用、主轴转速与径向切深耦合作用、轴向切深与径向切深耦合作用时，随着工艺参数的共同增加，GRG 均先减小后增大。当工艺参数全因素耦合时，GRG的最大值出现在高主轴转速、低进给速度、低轴向切深和低径向切深处，而GRG的最小值出现在中主轴转速、中进给速度、中轴向切深和高径向切深处。从整体看，低进给速度时GRG值更大，响应更优。

4 最优表面粗糙度预测

利用 Design-Expert 软件选择具有最高满意度值的过程条件组合作为响应的最佳条件，并找到最优目标响应。本文的最优目标响应为最大的GRG值。图8为GRG的最优目标响应及其工艺参数条件。最佳工艺参数条件为：主轴转速=15983.89r/min，进给速度=100mm/min，轴向切深=20.12μm，径向切深=0.1mm；最优目标响应为：GRG=0.903625，优于表2所示试验的最大GRG值，即第23组试验的GRG值。

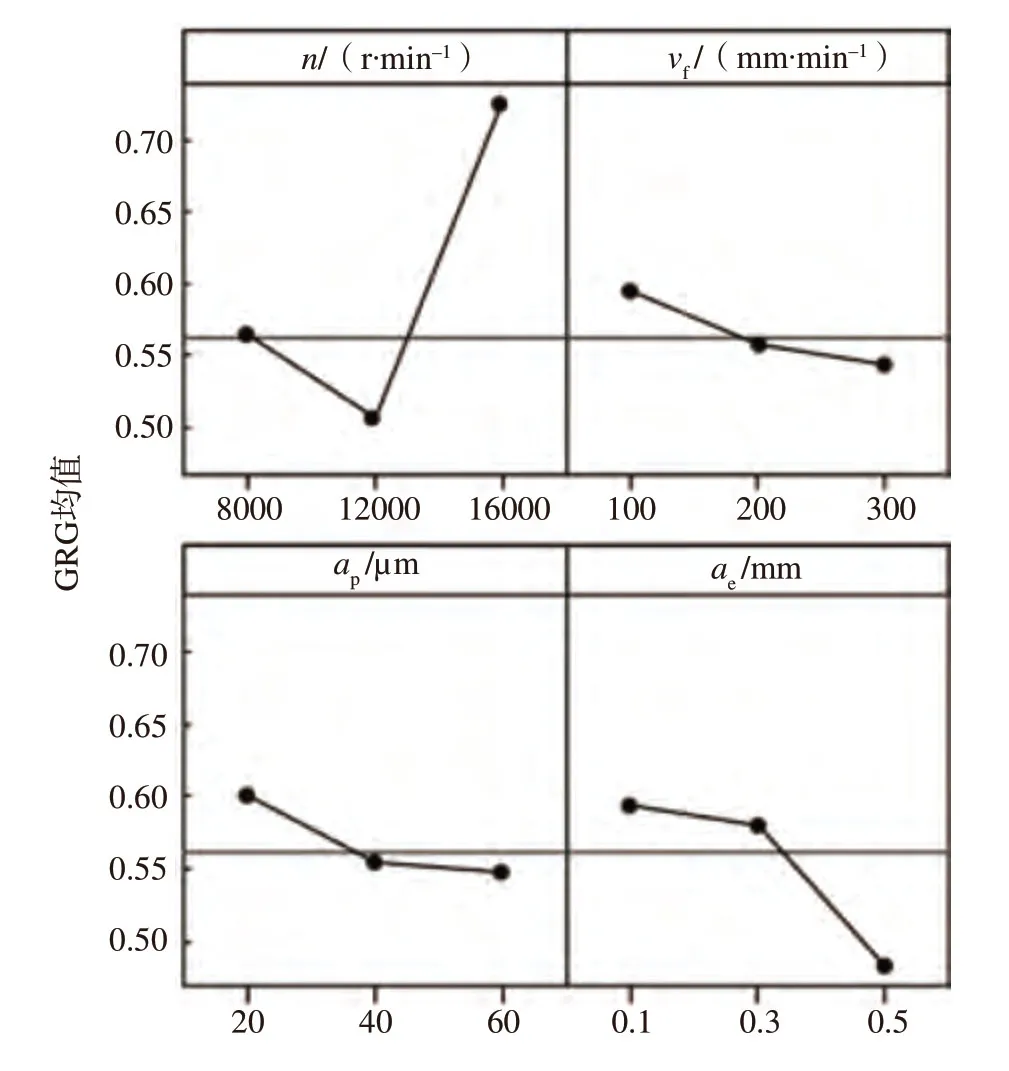
图5 GRG主效应图Fig.5 Main effect on GRG

图6 工艺参数耦合作用的F值Fig.6 F value of coupling effect of machining parameters

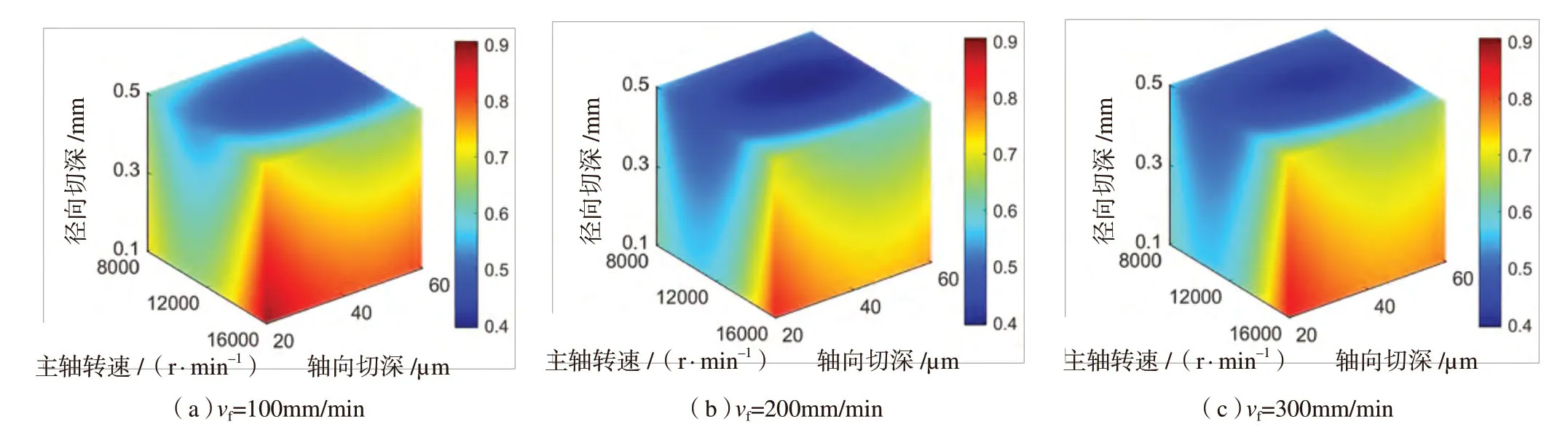
图7 GRG与微铣削工艺参数相关的响应轮廓Fig.7 Response profile of GRG related to micro-milling machining parameters

5 试验验证

为了验证模型预测的最优工艺参数水平的可靠性和有效性，选择设计试验中最优的试验参数组合即表2中第23组作为初始试验，前文中预测的最优参数组合作为对比试验，比较两组试验的GRG值，对优化结果进行验证，结果见表4。结果表明，验证试验的预测GRG值则比初始试验预测值增加了0.1197，验证试验的测量GRG值相较于初始试验测量值增加了0.1103，表明预测模型所得最优目标响应优于初始试验结果，优化结果相对于初始试验参数组合提高了15.27%，即GRG模型可用于优化微铣削工艺参数组合，实现更理想的表面粗糙度，证明了GRG 作为粗糙度检测指标对表面粗糙度能够进行更全面地评价。