基于机器学习的集群双向DAS能效技术
2020-11-11何春龙周月华钱恭斌
何春龙,周月华,钱恭斌,丁 雪
深圳大学电子与信息工程学院,广东深圳 518060
随着移动通信技术的快速发展,通信数据流量的爆炸式增长给未来通信网络带来了极大的挑战.为有效面对这些挑战,研究人员提出了虚拟小区、分布式天线系统(distributed antenna system, DAS)和设备间通信技术等颇具有创新性的方案.DAS可显著提高系统的频谱效率(spectral efficiency, SE)和能量效率(energy efficiency, EE)[1].然而,DAS在提高通信系统能效、降低通信能耗的同时,也给小区中的远程接入单元(remote access unit, RAU)与用户带来严重干扰[2].另外,在实际通信系统中,往往会同时存在上行链路和下行链路用户的双向通信[3].在大规模多输入多输出(multiple-input multiple-output, MIMO)系统中,文献[4]提出可动态分配上行链路和下行链路远程无线电头数量的双向动态网络(bidirectional dynamic network, BDN)传输策略.文献[5]分析了具有大规模MIMO的BDN中的系统性能,且通过数值仿真证明相较于动态时分双工系统,双向动态网络在频谱效率以及能量效率方面的优越性.在大型DAS中,为最大化双向动态网络中的频谱效率,文献[6]为使用户选择最有效的天线,提出一种新颖的分布式柔性天线集群(flexible antenna clustering, FAC)策略,并通获得比时分双工系统更好的SE性能.为使DAS更加符合实际情况,本研究将研究对象定为双向分布式天线系统(bidirectional distributed antenna system, BDAS).
对于更复杂的第5代(5th generation, 5G)无线网络,研究人员已开始将机器学习应用到无线通信领域.从系统设计和优化的角度,尤肖虎等[7]阐述了机器学习算法在5G无线通信系统中主要涉及3类技术问题:组合优化(如资源分配)、检测(如最优接收机设计)和估计(如信道估计),并指出人工智能(artificial intelligence, AI)技术是优于传统通信技术的替代解决方案.其中,聚类算法是无监督学习算法中的代表算法,被研究得最多,同时也是应用最广泛的算法.为有效降低通信时延并保证通信系统的稳定性,k均值(k-means)聚类算法被用于优化异构网络中的虚拟信道[8].LIANG等[9]运用k-means算法设计了MIMO通信系统的收发机.ALBAKAY等[10]在无线通信系统中运用k-means算法估计频率偏移,在确保低复杂度的情况下可显著提高通信系统的效率.在发射机信道估计中采用高斯混合模型(Gaussian mixture model, GMM)聚类算法可保证交换消息的完整性和真实性[11].LI等[12]应用GMM获取无线信道参数的分布,使用卷积神经网络(convolutional neural network, CNN)自动区分不同的无线信道.本研究提出基于机器学习的集群双向分布式天线系统(bidirectional distributed antenna system based on machine learning generated clusters, BDAS-MLGC)的功率分配方案,运用k-means和GMM集群算法构建基于机器学习的集群通信模式,并在此通信场景下探究最大化系统SE和EE的功率分配方案.
1 系统配置
BDAS-MLGC系统模型如图1.该系统模型考虑了上行用户和下行用户同时存在的场景,N个装有1个收发天线的服务基站(base station, BS)均匀分布在小区中.K个装有1个收发天线的蜂窝用户设备随机分布在小区中.其中,下行链路蜂窝用户的数为Kd, 上行链路蜂窝用户的数为Ku. 为便于分析,假设:① 服务基站不受来自它所发送和接收的信息之间的干扰;② 信道状态信息对于接收端和发送端均已知;③ 蜂窝用户共享相同的频谱资源;④ 将系统带宽归一化为1 Hz.

图1 BDAS-MLGC系统模型Fig.1 BDAS-MLGC system model
1.1 信道模型
在BDAS-MLGC系统中,第n个服务基站和第k个通信用户之间的信道状态hn, k可建模为复合衰落信道[13],数学表达式为
hn, k=gn, kwn, k
(1)
其中,gn, k和wn, k分别为第n(n=1, 2, …,N)个服务基站和第k(k=1, 2, …,K)个蜂窝用户之间的大规模衰落系数和小规模衰落系数.gn, k是一个独立同分布的零均值单位方差的循环对称复高斯随机变量.wn, k可表示[14]为
(2)
其中,c为以参考距离为1 km的中值平均路径;dn, k为蜂窝用户k到服务基站的距离,α为路径衰落系数,取值范围一般为[3, 5];sn, k是阴影衰落系数,服从对数正态分布,即10lgsn, k是一个高斯随机变量,均值为0,方差为σ2.
1.2 构建机器学习集群通信模式
运用集群算法构建BDAS-MLGC系统.
1.2.1 采用k-means集群算法构建机器学习集群
d维蜂窝用户的位置坐标分布数据集U={ui|ui∈Rd,i=1, 2, …,K,d=2}. 其中,ui为第i个蜂窝用户的位置坐标;K为小区中蜂窝用户的总数;d是用户位置坐标的维度,本研究设d=2.k-means集群算法[15]的目标是找到S个经集群分析后的蜂窝用户集群C={c1,c2, …,cS}的集群中心M={μ1,μ2, …,μS}, 从而使每个蜂窝用户uj(j=1, 2, …,K)与其所对应的最近的集群中心μi(i=1, 2, …,S)的距离和最小,该距离平方和为
(3)
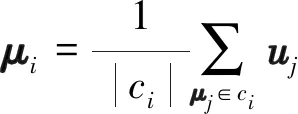
1.2.2 高斯集群算法构建机器学习集群
与使用蜂窝用户数据原型向量来描述聚类结构的k-means聚类算法不同,GMM聚类算法采用概率模式(高斯分布)描述聚类原型.根据文献[17]描述,可将高斯分布分量组合在一起用以构建整体概率模型,这意味着若它足够灵活,则可基于高斯混合分布来近似任何分布.因此,可使用GMM聚类算法,并通过高斯混合分量逼近所描述数据的分布,从而将BDAS-MLGC中的蜂窝用户数据的聚类原型描述为高斯分布的概率模式.具体来说,描述蜂窝用户聚类原型的高斯混合分布由S个混合分布分量组成,每个分量都是一个高斯分布,这S个高斯混合分布分量可表示为
(4)

(5)
在BDAS-MLGC中,给定d维蜂窝用户的位置坐标分布数据集U={uj|uj∈Rd,j=1, 2, …,K,d=2}. 令随机变量Zj∈{1, 2, …,S}表示用户uj的高斯混合分量.显然,Zj的先验概率P(Zj=i)对应着αi,i=1, 2, …,S. 根据贝叶斯定理,Zj的后验分布为
(6)
换句话说,PM(Zj=i|uj)表示由第i个高斯混合分量产生蜂窝用户样本uj的后验概率,为便于描述,记为rj, i(i=1, 2, …,S). 当已知高斯混合分布时,GMM聚类算法会将蜂窝用户样本集U划分为S个集群C={c1,c2, …,cS}, 并且每个蜂窝用户样本uj的集群标签λj为
(7)
对于给定的蜂窝用户数据集合U, 最大似然估计可表示为
(8)
式(8)的模型参数使用期望最大化(expectation maximize, EM)[18]算法通过迭代优化获得的,从而使GMM集群算法适应给定的蜂窝用户样本集合U. 在EM算法的第i次迭代过程中,每个高斯分量的混合系数为
(9)
式(9)表示每个高斯分量的混合系数由属于该分量的用户样本的平均后验概率确定.高斯混合分量的均值和协方差矩阵分别为
(10)
(11)
由式(10)可见,描述蜂窝用户聚类原型的高斯混合分布的每个混合成分的平均值可通过样本加权平均值估算,该加权平均值是每个用户样本属于该成分的后验概率.将GMM集群算法运用到BDAS-MLGC中进行用户集群分析的过程如图2.

图2 BDAS中的GMM集群算法伪代码
通过将k-means集群算法和GMM集群算法运用到BDAS,对用户进行集群分析后可得到每个蜂窝用户所在的集群和每个集群所在的集群中心.然后通过集群中心选择服务基站算法得到集群唯一的服务基站,可实现在BDAS中形成机器学习集群通信模式.此过程的具体步骤为:
1)通过机器学习中的非监督学习算法对蜂窝用户进行聚类分析.通过调用k-means集群算法(算法伪代码请扫描论文末页右下角补充材料图S1)与高斯集群算法(图2)对BDAS中的蜂窝用户进行聚类分析,令每个上行链路或下行链路用户都找到所属集群以及对应集群的集群中心.
2)通过蜂窝用户所在集群的中心为集群用户选择对应的服务基站.在执行步骤1)得到用户集群以及每个集群所对应的集群中心的基础上,运用集群中心选择服务基站的算法为集群用户选择唯一的服务基站,具体步骤见图3.




(12)
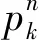
(13)
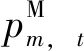
(14)
(15)
其中,ht, l为第t个上行蜂窝用户与第l个下行蜂窝用户之间的信道状态.
因此,BDAS-MLGC的总SE为
(16)
1.2.3 总功率消耗模型
由文献[19]可得,BDAS-MLGC中总功率消耗Ptotal包含发射功率消耗和额外的电路功耗两部分.令Ptrans表示在BDAS中采用机器学习集群通信模式下系统的总发射功率,则
(17)
额外的电路功耗Pcircuit包括与实际发射功率无关的动态功耗Pdy、 与处理单元以及电池有关的恒定静态功耗Pst和远程接入单元间连接光纤电路传输时的功耗P0. 因此,在BDAS-MLGC中总功率消耗模Ptotal可被改写[20]成
(N+Ku)Pdy+Pst+P0
(18)
其中,τ是射频频功率放大器的效率.
2 功率分配
2.1 最大化基于BDAS-MLGC的SE
BDAS-MLGC即满足下述3个约束条件的最大化系统SE的功率分配优化问题:① 上下行链路蜂窝用户的最小SE限制;② 服务基站的最大发射功率要求;③ 上行链路蜂窝用户最大发射功率要求.结合式(17),可把机器学习集群通信模式下最大化系统SE的优化问题建模为
(19)
(19a)

(19b)

(19c)

(19d)

首先,定义P1=[PMu,PMd] 为优化变量,fSE(P1)为目标函数.再由(16)可知,优化问题(19)仍具有非凸性及非线性特征,因此,运用基于凸函数差分(difference of convex function, DC)[21]优化理论对式(19)进行转化为两个凹凸部分的和的形式,可以表述为
(20)
其中,
(21)
(22)
用C1表示式(19)中的约束集,它表明满足最小SE限制的约束条件(19a)和(19c)是非线性,因此可将(19a)和(19c)转换为如式(23)和式(24)的线性表达式.
(23)
(24)
在BDAS-MLGC中,满足上述约束条件的最大化系统SE的优化问题,可转化为具有凸约束集的DC优化问题,即
s.t. 式(19a)—式(19d)
(25)

(26)


2.2 最大化BDAS-MLGC的EE
文献[23]将能量效率定义为频谱效率与消耗总功率的比值.因此,BDAS-MLGC的能量效率为
(27)
BDAS-MLGC是在满足以下3个约束条件的基础上实现最大化系统EE的功率优化问题.这3个约束条件为:① 蜂窝用户的最小SE限制;② 基站的最大发射功率限制;③ 用户的最大发射功率限制.结合式(18)和式(27)可把机器学习集群通信模式下最大化系统EE的优化问题建模为
(28)

(28a)

(28b)

(28c)

(28d)
其中,P2=[PMu,PMd]为优化变量.由式(28)可得,BDAS-MLGC中的最大化系统EE问题是一个具有分式形式的优化问题,运用分式规划(fractional programming, FP)理论[24],可将具有分式形式的优化问题式(28)转化为含有减法结构的等价优化问题,即
(N+Ku)Pdy+Pst+P0}
s.t.式(28a)—式(28d)
(29)
其中,ω1是一个被引入的标量.当定理1被满足时,任何一个具有类似分式规划的函数都可被等价近似为一个具有减的形式的非分式规划问题[24].

由定理1可知,式(28)和式(29)之间的等价性[25].用FP理论调整后得到的等价优化问题(29)可再次被重写为如式(30)的带有DC结构的优化问题.
s.t.式(28a)—式(28d)
(30)
式(30)中的凹函数和凸函数部分可分别写成
(31)
(32)

(33)


3 仿真结果


表1 BDAS-MLGC仿真参数

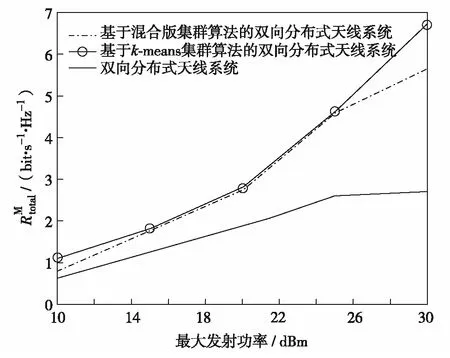
图7 系统SE随最大发射功率增大变化曲线Fig.7 SE versus the maximum transmit power
图8显示了系统的EE随最大发射功率从10 dBm增至30 dBm变化的情况.从整体上看,两种通信模式下系统的EE都随服务基站的最大发射功率的增大呈先增而后降趋势.但是在BDAS中采用基于机器学习的集群通信模式后系统的EE比于单一的BDAS的EE有了很大的提高.由图8可知,当服务基站的发射功率较小时BDAS-MLGC的EE增长速度非常快,且当服务基站的发射功率为20 dBm时,系统的EE达到最大值,而单一的BDAS的EE的增长速率非常缓慢.另外,在BDAS中采用k-means集群算法和GMM集群算法后得到的EE皆高于单一的BDAS.例如,当服务基站的最大发射功率为20 dBm时,使用k-means聚类算法和GMM聚类算法构建的BDAS-MLGC实现的系统的EE比单一的BDAS的系统EE分别高出近35%和34%.可见,BDAS-MLGC可有效提升系统的EE.

图8 系统EE随最大发射功率增大变化曲线Fig.8 EE versus the maximum transmit power
为更深入地了解在BDAS中使用机器学习算法的优势,比较在单一的DAS中和基于机器学习的DAS中进行功率分配时算法的复杂度.由文献[26]可知,内点法在最坏情况下复杂度达到O(1/ζ). 其中,ζ为误差容忍度参数.因此,在单一的BDAS中进行功率分配时,使用内点法的算法复杂度为O(tNKL). 其中,t为迭代次数;L=1/ζ;N为服务基站数目;K为小区中蜂窝用户总数.分别从相关文献[27-28]中,可得出k-means聚类算法和GMM聚类算法的复杂度分别为O(t(S+K)d)和O(tSKd3), 其中,S为集群数目;d为用户坐标位置的维度.由k-means和GMM实现的基于机器学习集群算法的计算复杂度为O(tKL+t(S+K)d)和O(tKL+tSKd3).结果表明,在BDAS中使用机器学习集群算法能够极大程度地提高系统的通信性能.
结 语
在BDAS中,上行用户和下行用户的同时存在导致通信系统中存在更多的干扰,同时复杂的干扰管理会给中心处理基站带来沉重的计算负担.为此,本研究将机器学习算法引入BDAS中构建BDAS-MLGC.首先,引进集群算法对蜂窝用户进行集群分析,从而得到相应的集群以及集群中心;然后,按照集群中心选择服务基站算法来确定每个集群的服务基站,同时对应的上行或下行用户会被分配到相应的机器学习集群,这样就构建了基于机器学习的集群通信模式.在此通信模式下,讨论在满足一定约束条件下的最大化系统SE和EE的功率分配方案.仿真结果表明,相比单一的BDAS,BDAS-MLGC显著提高了系统的通信性能.
