一种低信噪比环境下的语音端点检测算法

2020-11-10卜玉婷曾庆宁郑展恒

声学技术 2020年5期

卜玉婷，曾庆宁，郑展恒

(桂林电子科技大学“认知无线电与信息处理”教育部重点实验室，广西桂林541004)

0 引言

端点检测(Endpoint Detection,ED)，通常是指在存在背景噪声的情况下检测出语音的起始点和结束点，它在语音信号处理中至关重要，如语音增强、语音识别、编码和传输等[1]。随着智能家居的普及，对语音产品的性能要求也越来越高，人们希望在远场或者嘈杂的环境中也能用语音控制智能设备，因此研究低信噪比环境下高效的语音控制技术具有一定的实际应用价值。

端点检测是一种常用的语音信号前端处理技术，语音端点的准确定位有助于排除噪声段的干扰、增强系统处理的实时响应性、降低功耗从而提升系统性能。传统算法主要采用语音特征参数进行检测，通常可划分为时域和频域两大类，在时域中，短时能量、短时过零率、短时相关性特征[2]被广泛应用；在频域中，谱熵、方差[3]、倒谱距离[4]、小波变换等特征也被认为是端点检测的有效参数。端点检测的性能和信噪比(Signal to Noise Ratio,SNR)密切相关，低信噪比环境下的端点检测一直是研究的热点之一[5]。近年来提出了许多改进的端点检测算法，如文献[2]提出了一种调制域谱减结合自相关函数的端点检测算法，因加入了去噪过程使得在低信噪比下减少了误判；文献[4]通过执行多频谱估计的谱减法增强语音，再利用Mel倒谱距离进行检测，并且采用自适应阈值可应用于不同环境。但是，上述算法的检测精度仍有待提高。

考虑到上述算法的优缺点，本文研究了一种适用于非平稳噪声环境的语音端点检测算法，通过对带噪语音进行瞬态干扰抑制以及调制域谱减[6]获得降噪和语音失真之间的平衡，从而改善语音质量，再结合功率归一化倒谱系数(Power Normalized Cepstrum Coefficient,PNCC)[7]之间的距离进行端点检测。实验表明，该算法在低信噪比环境下仍然有效且具有一定的抗噪鲁棒性。

1 瞬态噪声抑制

越来越多的研究在端点检测前增强了语音，这对端点检测的准确性有重要影响。传统的语音增强技术利用时间平滑来估计噪声的功率谱密度(Power Spectrum Density,PSD)是不够的，因为实际生活中出现的大多都是非平稳噪声，如典型的瞬态干扰：键盘敲击、敲门声等，具有时间短、频域广等特点，会对语音造成极大的干扰。因此提高算法在复杂环境中的稳健性具有广泛的研究意义。

1.1 瞬态PSD估计

利用语音、瞬态噪声、背景噪声的不同变化率，引入一个可跟踪瞬态信号快速变化的最优改进对数谱幅度估计(Optimally-Modified Log-Spectral Amplitude Estimator,OM-LSA)算法[8]，通过分配一个较小的平滑参数来调整OM-LSA的噪声PSD估计分量，以跟踪输入信号频谱的瞬态变化。

假设x(n)为语音信号，d(n)为加性平稳噪声、t(n)为瞬态噪声，被测信号y(n)表示如下：

算法整体的流程图如图1所示。

信号经过加窗、快速傅里叶变换(Fast Fourier Transform,FFT)后可实现短时傅里叶变换(Short Time Fourier Transform,SFFT)，然后对最小控制递归平均(Minima Controlled Recursive Averaging,MCRA)的平滑参数进行调整再加入反因果窗区分瞬态，可为修正的 OM-LSA算法提供准确的噪声PSD估计。

图2为改进的噪声PSD估计算法流程图，虚线框图为调整部分，具体改进如下：

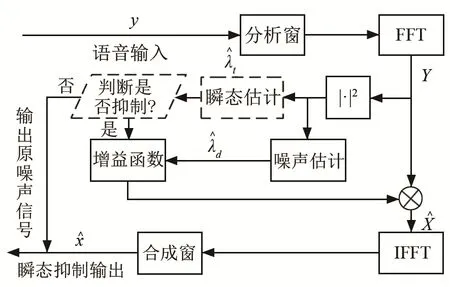
图1 瞬态噪声抑制原理图Fig.1 Principle diagram of transient noise suppression

(1)平滑处理

y(n)由瞬态分量和非瞬态分量(语音和噪声)构成，利用上述算法估计非瞬态分量的 PSD，图中Y 、分别表示含噪语音在时频域做短时傅里叶变换的幅度值以及测量信号Y的估计值，则为瞬态噪声的功率谱估计值以及平稳噪声信号的功率谱估计值，噪声信号功率谱估计基于一个对频谱幅度进行时间递归平均获得的周期图，其中当前帧含噪语音的功率谱S(k,l)可表示为

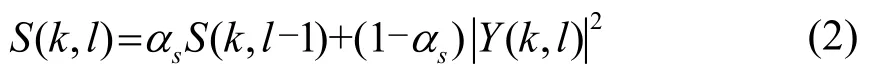
为了更快跟踪采用一个较小的平滑参数αs，其值越低，对当前时间的估计越准确，瞬态信号能迅速被捕捉到，通过实验将其从0.9～0.99调整为0.7。

(2)最小值搜索

瞬态存在信号由平滑周期图的极小值控制，该极小值由长度为L的有限因果窗得到：

但由于语音开始时也是突发的，不能通过频谱递归平滑来跟踪，其容易被误判为瞬态信号，根据瞬时信号功率衰减快、语音信号开始后功率水平保持稳定这一特点引入一个长度为40 ms的反因果窗来实现二者的区分。

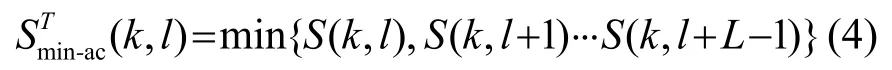
计算因果窗和反因果窗两个最小谱值的最大值，并将其作为修正的周期图的极小值参与瞬态决策：

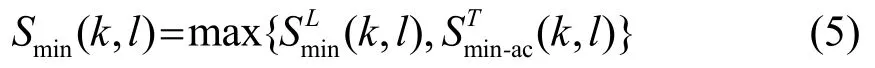
进一步地，通过以下规则做出瞬态存在决策，其中δ为经验阈值，I(k,l)为瞬态信号指示器，p(k,l)为瞬态存在概率：

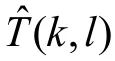
图2 改进的噪声功率谱密度估计Fig.2 Improved noise power spectral density estimation

1.2 瞬态抑制执行判断

为了提高算法执行效率，对估计出来的瞬态信号分成很多短时帧，对每帧信号能量进行递减排序。设定比例因子η，η∈(0,1)，以η为基准对该帧内排序好的两部分数据求取能量均值。若二者相差倍数超过阈值T1则粗略判定该帧存在较多瞬态噪声，记为瞬态噪声帧。对总的语音帧求取瞬态噪声帧总和，若超过阈值则判定该语音含有复杂瞬态冲击噪声，若不是则输出含噪语音，后续算法可对其进行消除。无需采用瞬态抑制，有效提高程序运行速度、降低复杂度，若是则进行瞬态噪声抑制。

1.3 瞬态噪声抑制

瞬态干扰抑制的加入使得算法对键盘敲击声、敲门声等非平稳噪声具有一定抑制作用，为了验证算法对非平稳瞬态噪声的抑制能力，图3给出了信噪比为 0 dB的瞬态抑制前后波形图，通过对比图3(a)、3(b)、3(c)，给出了非平稳瞬态噪声的一个有效估计，图3(d)中大部分瞬态冲击噪声被抑制，但是还存在一定的背景噪声，后续引入调制域谱减法对其进行消除。

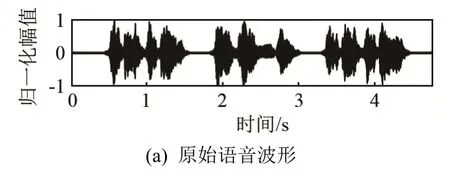
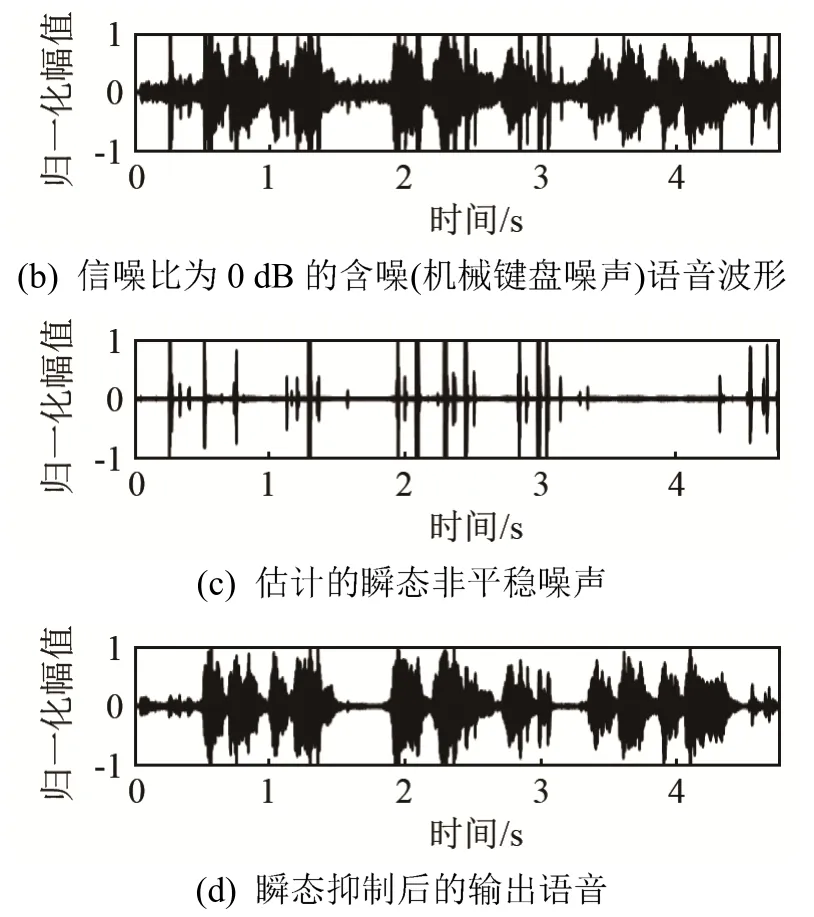
图3 语音增强前后波形对比图Fig.3 Waveform comparison chart before and after speech enhancement

2 调制域谱减法

2.1 调制域

人们测试和分析信号一般通过时域和频域来实现。近年来由于调频技术的快速发展，调制域处理在语音编码、语音识别等领域的应用日益普及[10]。与频域表示的是频率与幅度间关系和时域表示时间和幅度间关系不同，调制域是时间和频率之间的关系，其相互关系可表示如图4[2]。

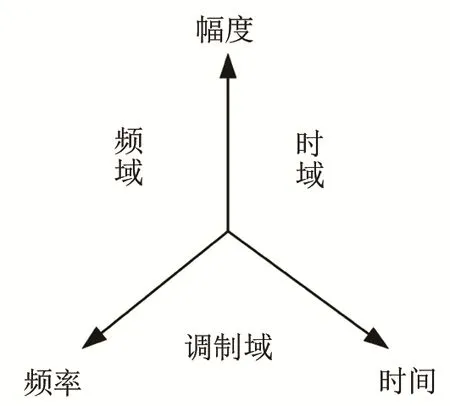
图4 时域、频域、调制域之间的关系Fig.4 The connection between time domain,frequency domain and modulation domain

2.2 调制域谱减

谱减法是一种直观而有效的单通道降噪算法，但在低能量语音区域做谱减处理时会引入音乐噪声，为了解决上述问题，Paliway等[6]在2010年首先提出调制域谱减算法，通过在调制域中执行谱减法并合理选择调制帧长度，可以有效避免音乐噪声带来的语音失真。

传统意义上的调制频谱可以认为是带通滤波信号强度包络的傅里叶变换，然而在研究中一般采用短时傅里叶变换代替带通滤波。其中，与带通滤波信号强度包络最接近的特征量是幅度谱平方。声学幅度谱的包络表示声道的形状，而调制谱表示声道随时间变化的情况，正是这些时间动态变化包含了大量的语音信息，故采用在调制域中应用谱减算法来使在语音增强过程中引入的失真最小化。

假设噪声和语音不相关，含噪信号可表示为：

其中：x(n)为纯净信号；d(n)是经瞬态抑制后残余的噪声，其频谱不随时间变化，n为离散时间的索引。由于语音的短时平稳特性，对信号y(n)进行预处理后做STFT，可得：

为了直观地表达出信号的幅度谱和相位谱，可将变换后的频谱表示为极坐标的形式：

式中：k为离散频率。沿时间逐帧对幅度谱|Y(n,k)|进行STFT，得到调制谱：

其中：|Y(τ,k,m)| 和 ∠ Y(τ,k,m)分别为含噪语音的调制幅度谱和调制相位谱。得出调制频谱后将传统谱减法应用在调制域以降低噪声的干扰，具体谱减表达式如式(15)所示：

其中：ϑ是遗忘因子。当信号判定为噪声段时，更新噪声估计。

2.3 调制域相位补偿

传统的谱减法一般只对幅度谱进行修正，而忽略了相位谱对语音的影响，这是由于长期以来，研究者认为带噪语音的相位是纯净语音相位的最佳估计，然而在低信噪比环境下，带噪语音相位失配会导致语音变得粗糙，从而影响语音的可懂度。

最近的研究表明，语音的调制相位比频域相位包含有更多的信息，通过对调制相位谱进行补偿可以在一定程度上提升语音质量，减少音乐噪声[11]。

因为带噪信号为实信号，故经过STFT得到的调制谱是共轭对称的，通过使用反对称函数去修正角度，从而补偿相位，相位补偿函数表达式为

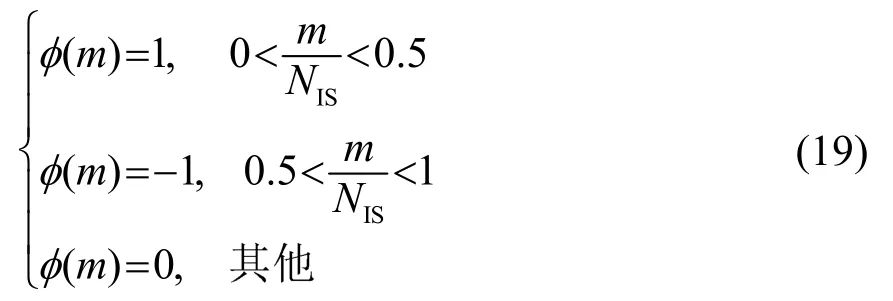
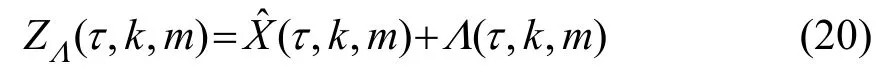
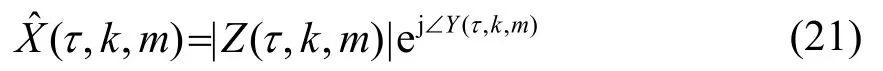
修正的调制域相位谱如式(22)所示：

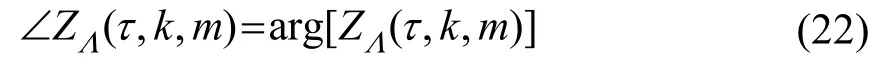
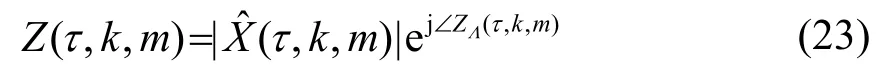
将最终得到的调制谱做快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)、去窗处理和重叠相加得到增强后的频域幅度谱[12]。

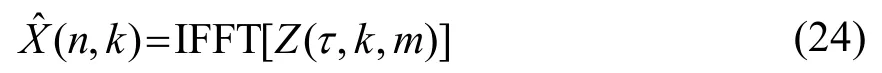
最后结合频率相位谱再一次进行IFFT，即可得到谱减降噪后的语音信号。

调制域谱减原理流程图如图5所示。

为了检测瞬态噪声抑制结合调制域谱减算法的性能，实验采用了Noisex-92噪声库中的white、f16噪声以及真实环境录制的机械键盘声、敲门声，SNR设为5、0、-5、-10 dB。仿真实验从语音时域波形对比、信噪比提升以及语音质量感知评估测度(Perceptual Evaluation of Speech Quality,PESQ)三个方面验证算法的性能。参考算法分别为基本谱减法、多带谱减法和对数最小均方误差(Logarithm Minimum Mean Square Error,LogMMSE)算法。

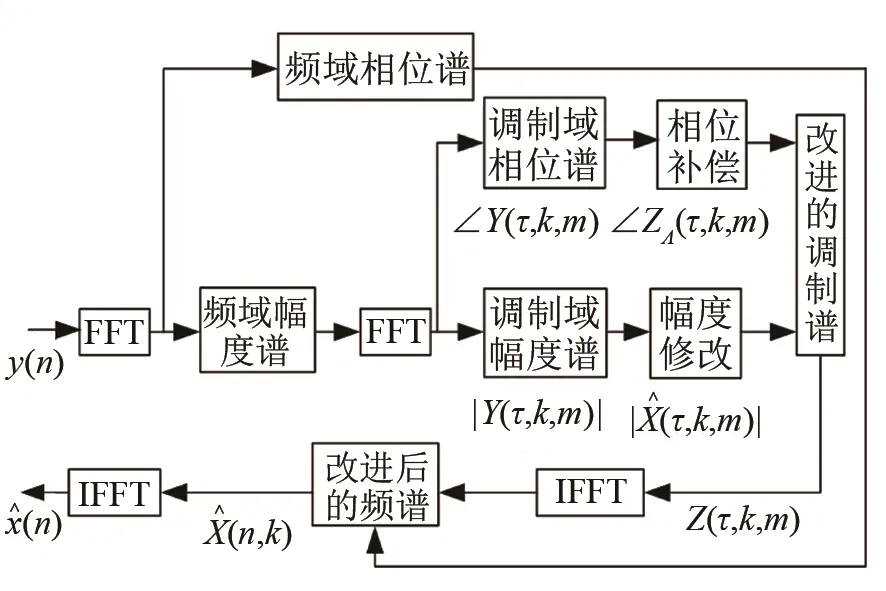
图5 调制域谱减法流程图Fig.5 Flow chart of modulation domain spectrum subtraction

对于平稳噪声，上述算法均有不错的效果。因此主要测试算法在非平稳噪声环境下的稳健性。图6为一段混合机械键盘敲击声的含噪语音经上述各算法处理后的时域波形图，其中信噪比为-10 dB。由图 6(c)～6(e)这三种算法的对比波形图可知，三者对于瞬态冲击噪声的抑制能力较弱，仍旧存在很多冲击噪声导致语音失真。由图 6(f)可知，提出的算法对于非平稳噪声有很强的抑制能力，同时对语音产生的畸变小，残留噪声少。

图6 不同算法在机械键盘噪声环境下SNR为-10 dB的语音增强效果Fig.6 Enhancement effects of different algorithms in a mechanical keyboard noise environment of SNR is -10 dB

表 1为各算法在不同环境下的信噪比提升对比。从表1中可以看出，结合瞬态抑制的调制域谱减算法相对于其他算法在信噪比提升上更具优势，尤其是非平稳噪声情况下，相对于其他算法其抗噪稳健性强，有利于后续端点检测的判定。

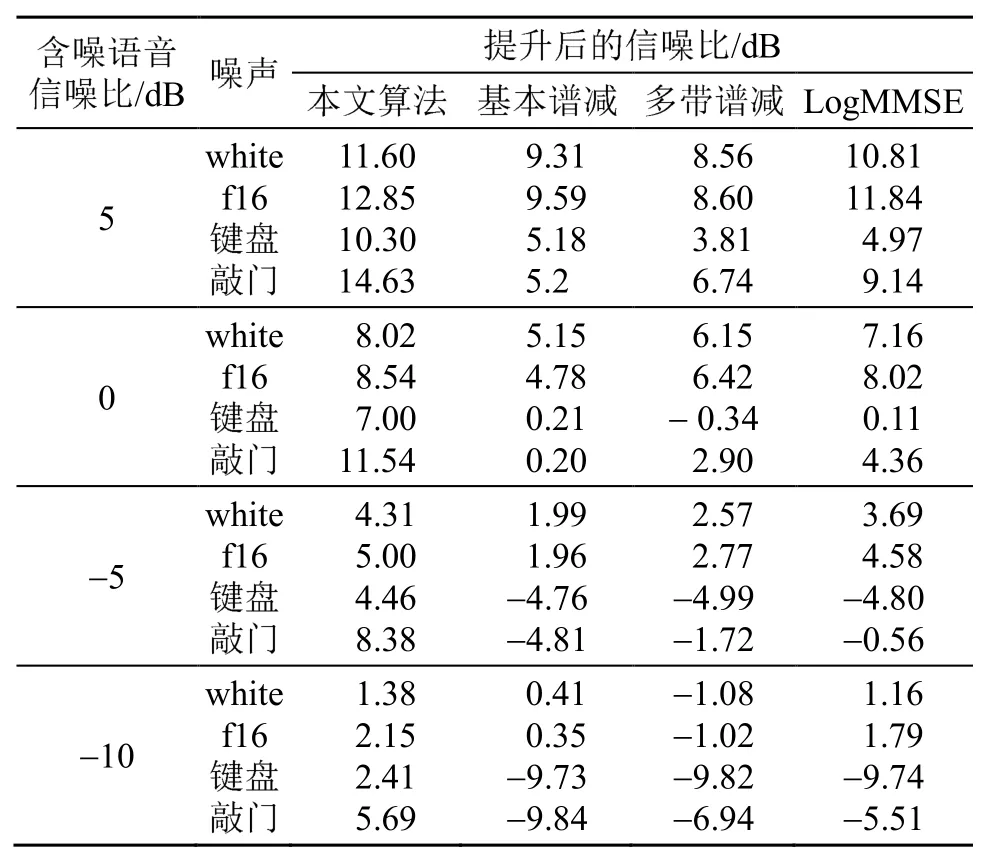
表1 各算法在不同环境下的信噪比提升前后对比Table 1 Comparison of SNR enhancement between different algorithms in different environments

为了进一步验证算法的性能，采用反映语音可懂度的感知语音质量评估测度(PESQ)，PESQ的评分范围为[-0.5,4.5]，通常情况下分数越高，语音可懂度越好，越有利于后续处理。

图7显示了各算法在机械键盘噪声环境下不同SNR时的PESQ得分。由图7可知，随着SNR变差，相关的PESQ分数总是变低，表明PESQ是反映语音中嘈杂失真程度的适当度量。相比参考算法，提出的算法在所选取的机械噪声环境中取得了良好的语音增强效果，减少了语音畸变。

算法在语音时域波形图、信噪比提升以及感知语音质量评估测度3个指标中均表现良好，故本文算法将其用于前端消噪以提升信噪比，减少语音失真，从而为后续端点检测提供良好基础。

图7 各算法在机械键盘噪声环境下感知语音质量评估(PESQ)测度Fig.7 The perceptual speech quality assessment(PESQ)metrics of different algorithms in a mechanical keyboard noise environment

3 PNCC倒谱距离端点检测

3.1 功率归一化倒谱系数

特征提取是语音信号处理中的关键步骤，其目的是提取有效的声学特征参数集。目前使用最广泛的特征提取算法是梅尔频率倒谱系数(Mel-Frequency Cepstrum Coefficients,MFCC)[13]，但MFCC最具挑战性的问题之一是在噪声环境较理想的情况下识别精度较高，但是在低信噪比环境下其识别准确率会急剧下降，无法满足实际应用需求。

最近由美国科学家Kim等[7]提出的功率归一化倒谱系数(Power Normalized Cepstrum Coefficient,PNCC)特征提取算法已经被开发用于增强语音识别系统在噪声环境中的鲁棒性，其可以看作在MFCC基础上改进的一种特征提取算法，与MFCC相比，在不损失识别精度的情况下，语音识别系统的抗噪鲁棒性有了一定提升[14]，具体的PNCC特征提取步骤如下：

(1)对语音进行预处理，包括采样量化、预加重、分帧加窗和STFT等。

(2)对时频域转换分析后的序列进行功率谱计算，其公式为

其中：FT(ω)是经过短时傅里叶变换以后得到的值。

(3)采用伽玛通(Gammatone)听觉滤波器组对获得的功率谱进行滤波，该滤波器组的时域冲激响应为

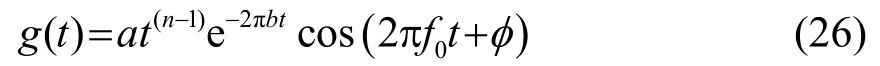
其中：n为滤波器阶数；b为滤波器带宽。

(4)通过计算长时帧功率、采用非对称滤波和临时掩蔽抑制背景噪声，长时帧功率计算公式为

其中非对称滤波器公式为

(5)采用时-频域归一化处理调整功率，过程为

(6)进一步将经过幂函数非线性处理后的信号序列通过离散余弦变换(Discrete Cosine Transformation,DCT)进行特征降维得到特征参数。

(7)最后通过倒谱均值归一化(Cepstrum Mean Normalization,CMN)[16]减去短时帧倒谱域上的信道均值响应，从而避免倒谱域上信道卷积噪声的干扰，最终得到PNCC特征参数。

MFCC和PNCC算法流程图如图8所示。

由图8对比MFCC特征提取算法可知，PNCC算法改进的特性包括：

(1)PNCC使用基于Gammatone滤波器形状的频率加权，其临界频带中心频率附近的声音特征比三角滤波器更加集中，且两侧过渡平滑可减少相邻频带之间频谱能量的泄漏。

(2)在MFCC提取过程中，当输入能量值较小时由于对数函数的缺陷可能导致输出能量的剧烈变化。而 PNCC通过精确选择幂律非线性来替代MFCC处理中的对数非线性，以近似模拟信号强度和听觉-神经发射率之间的非线性关系。生理学家认为，这是对给定的短时信号强度的测量，通过这种非线性来抑制小信号及其可变性以保证鲁棒性[7]。

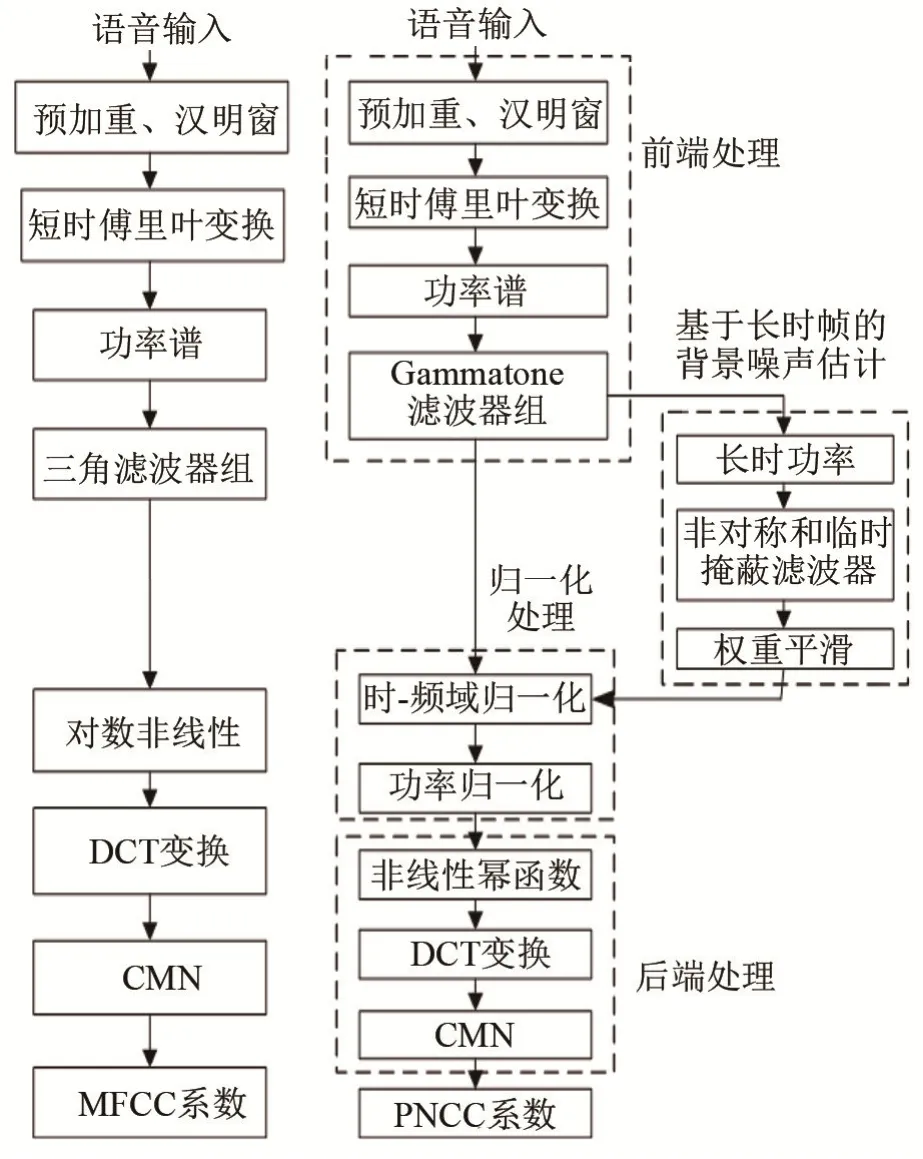
图8 MFCC、PNCC特征提取算法结构Fig.8 Structure of MFCC and PNCC feature extraction algorithm

(3)引入抑制背景激励的非对称滤波算法，然后通过在低于包络线时抑制瞬时功率来执行时间掩蔽。

3.2 功率归一化倒谱距离的端点检测算法

1993年，英国的Haigh等[17]将加权欧式距离引入倒谱领域，定义了倒谱距离，并首次提出了基于倒谱距离的端点检测算法，随后又出现了一些改进方案，例如自适应倒谱距离[18]、MFCC倒谱距离[19]等。语音帧和噪音帧的倒谱差异较大，故采用倒谱距离作为端点检测参数。

传统的倒谱距离抗噪声性能差，检测效果不理想，因此有必要对传统算法进行改进以增强低信噪比环境下的检测性能。基于此，本文研究了一种采用非平稳噪声抑制和调制域谱减进行前端增强并结合功率归一化倒谱距离的端点检测算法。该算法能有效区分语音和噪声，抗噪鲁棒性好，其中PNCC采用 Gammatone听觉滤波器组，可以提供人类听觉感知的精确表示。

因此，选用非平稳噪声抑制结合调制域谱减降低噪声的干扰，再采用PNCC倒谱距离可以在检测准确度方面提供实质性的改进。

本文算法具体步骤如下：

(1)对含噪语音进行瞬态噪声抑制再结合调制域谱减并补偿相位得到增强后的语音。

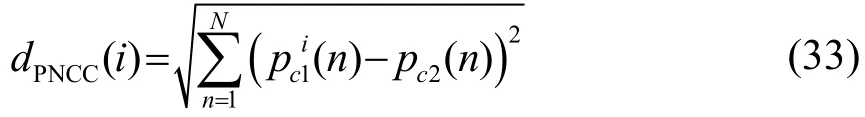
式中：N为功率归一化倒谱的分析阶数，本文采用16阶。

(3)由式(33)计算出 PNCC倒谱距离，最后采用单参数双门限判决方法，依据经过平滑后的数据值选定两个阈值 T1、T2，当 PNCC倒谱距离高于T2阈值时确定是语音，再依据与T1值的大小来判定语音端点。

4 实验与分析

4.1 实验配置

实验使用 M-Audio多路音频设备在相对安静的办公室采集语音数据。为模拟智能音箱场景，分别在1～4 m，全方位进行音箱命令词录制，每条语音时长约为4～5 s，其中非平稳噪声是模拟办公环境中的机械键盘声以及敲门声真实录制的。为了直观地对比算法的端点检测结果标定，采用的语音内容为三个命令词：“小白小白”“打开音箱”“小白小白”的语音文件。采样频率为 16 kHz、精度为16 bit，采用汉明窗进行分帧。将语音与 Noise-92噪声库中的white、f16以及录制的机械键盘、敲门声4种噪声分别混合成SNR为5、0、-5、-10 dB的带噪语音进行测试以评估各算法性能。

4.2 实验结果与分析

为验证本文算法在低信噪比下的可行性，分别从谱减、倒谱距离两方面有针对性地选取了4个对比算法，分别是：王瑶等[2]于2018年提出的调制域谱减结合对数能量和自相关函数峰值比的端点检测算法，该算法使用对数能量替代端点检测中经典的短时平均能量，使用自相关函数主峰比值替代平均过零率；王群等[19]于 2017年提出的调制域谱减和对数能量子带谱熵相结合的端点检测算法；朱春利等[20]于 2019年提出的基于多特征融合与动态阈值的端点检测算法，该算法先经过谱减再结合MFCC倒谱距离、均匀子带频带方差特征，利用双参数双门限法进行端点判定；多带谱减结合倒谱距离的端点检测算法。其中文献[2]和文献[19]与本文的相似点是前端增强均采用了调制域谱减，所不同的是本文算法增加了一个非平稳噪声抑制模块，使算法具有更强的稳健性，同时各算法端点检测参数是针对不同传统方法的分别改进。为方便起见，上述4种算法简记为文献[2]算法、文献[19]算法、文献[20]算法以及多带谱减结合倒谱距离法。

测试语音在SNR为-10 dB的机械键盘噪声环境下经各算法的端点检测结果显示如图9～13所示。

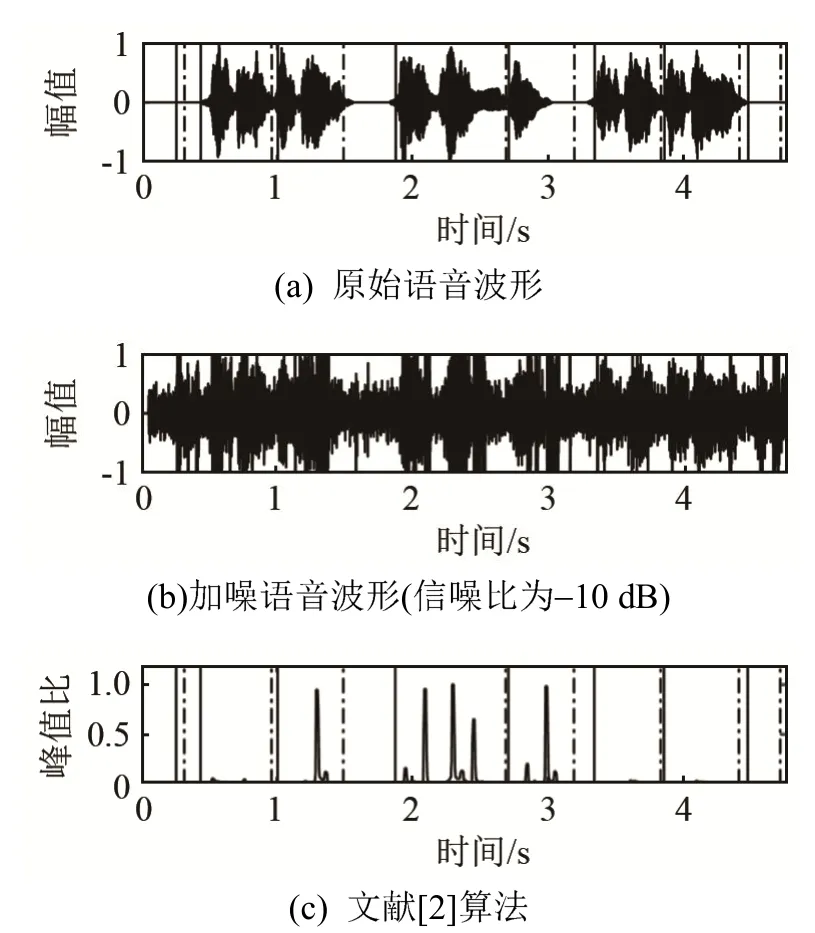
图9 文献[2]算法端点检测结果Fig.9 The endpoint detection results of the method in Ref.[2]

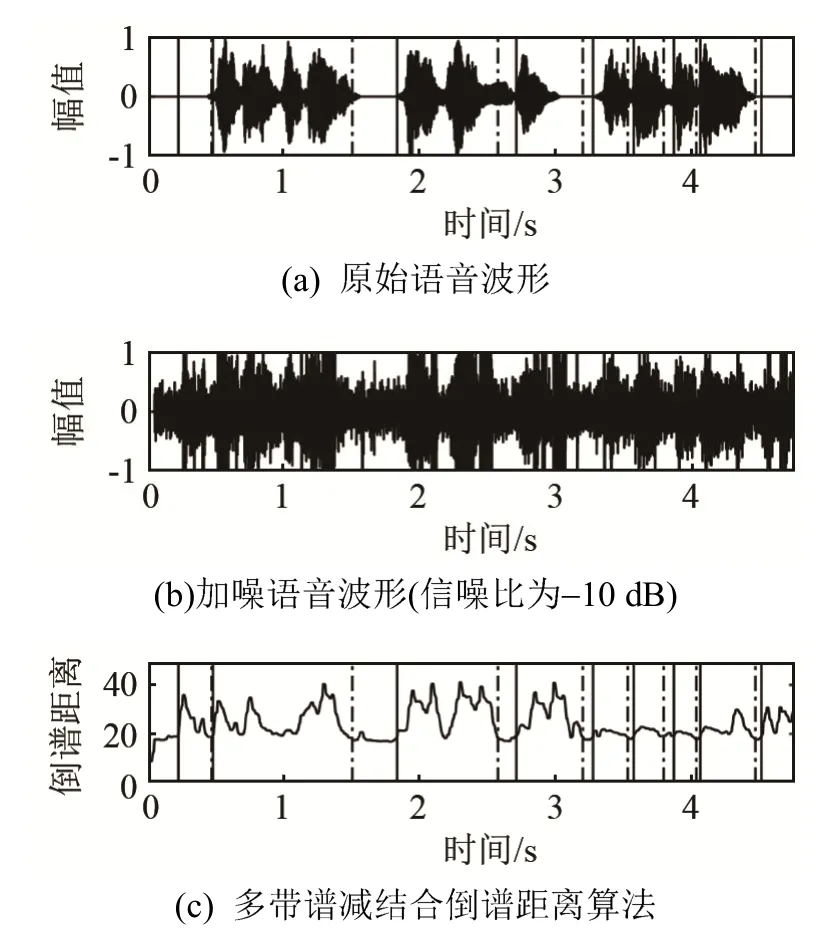
图10 多带谱减结合倒谱距离法端点检测结果Fig.10 Endpoint detection results by multiband spectrum subtraction combined with cepstrum distance method

图11 文献[20]算法端点检测结果Fig.11 The endpoint detection results of the algorithm in Ref.[20]

图12 文献[21]算法端点检测结果Fig.12 The endpoint detection results of the algorithm in Ref.[21]

图9～13中的图(a)为原始语音波形，为方便对比，将各算法得出的检测结果也在图(a)中表示，其中黑色实线代表语音的开始，点划线代表语音的结束。图(b)为-10 dB含噪语音。由图9～13可知，在低信噪比环境下，由于不同说话人换气长度不一致，字词间隔的语音能量可能会被嘈杂环境中的噪声掩盖从而被误判为噪声，导致丢失部分语音。图9中文献[2]算法对语音端点的判断基本正确，但是在开头和结尾处将过大的冲击噪声错误地判定为语音。显然图 10中的多带谱减结合倒谱距离端点检测算法也存在类似问题，而且在语音段出现了多处间断，其对端点的判定不理想。图11中文献[19]由于部分语音能量较低，出现了漏检，对于语音端点边界定位不精确。图12中文献[20]对语音开始和结束位置判决精度不高，出现了大量的错检，把噪声判定为语音。而图 13所示的本文算法在相应条件下有效减少了错检和漏检率。这是因为采用噪声抑制算法消除了大量容易被误判为语音的瞬态冲击噪声，再经过调制域谱减消除残余噪声，有效提高了信噪比并避免了音乐噪声，而PNCC倒谱系数本身较 MFCC倒谱系数具有一定的抗噪性，且PNCC倒谱距离曲线在噪声段波形平坦，过渡到语音段时，曲线窄而陡峭，因此可以提高端点位置判决精度。由于语音是非平稳信号，PNCC采用的语音长时帧信息可用于分析其非平稳性，可有效弥补倒谱距离特征在非平稳噪声下性能不佳的缺陷，同时算法将“小白小白”等命令判定为一段语音，而不是将每个字词单个检出，保证了语句的连贯性。

图13 本文算法端点检测结果Fig.13 The endpoint detection results of the algorithm in this paper

为了更直观地评估各算法的检测准确率，分别对4种噪声环境下录制的语音库文件进行测试，取20条录制的语音端点检测正确率的平均值进行对比，其中正确率可用下式计算得到[20]：

错误帧数=噪声帧检测为语音帧数+语音帧检测为噪声帧数；

正确率=(总帧数-错误帧数)÷总帧数×100%

图14～17分别为white噪声、f16噪声、机械键盘噪声、敲门噪声环境下各算法的端点检测正确率对比图。

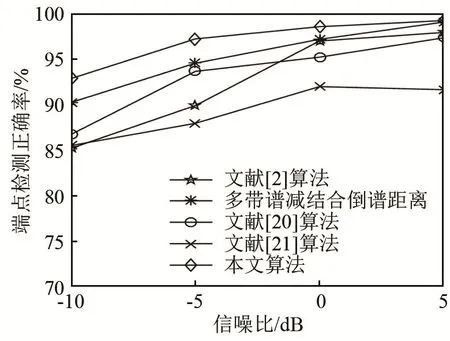
图14 不同算法在white噪声环境下端点检测正确率比较Fig.14 Accuracy comparison of endpoint detection by different algorithms in white noise environment

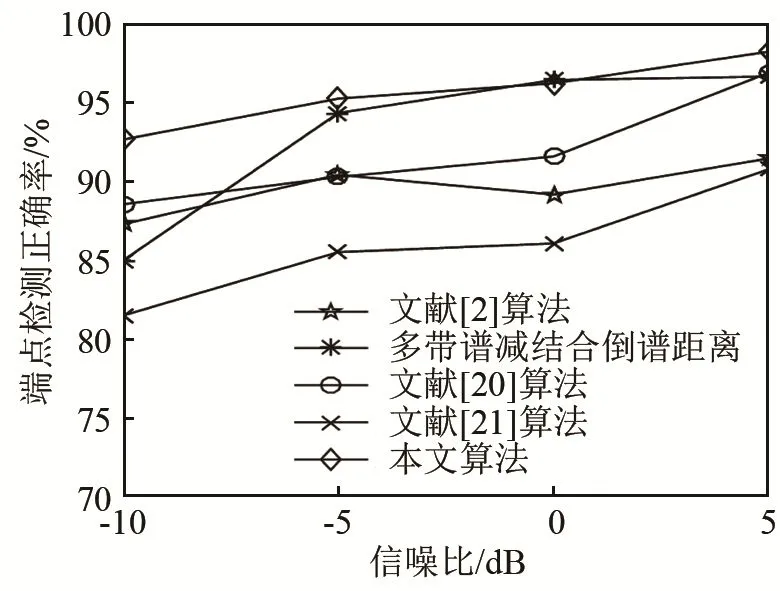
图15 不同算法在f16噪声环境下端点检测正确率比较Fig.15 Accuracy comparison of endpoint detection by different algorithms in f16 noise environment

图16 不同算法在机械键盘噪声环境下端点检测正确率比较Fig.16 Accuracy comparison of endpoint detection by different algorithms in mechanical keyboard noise environment

对比图 14～17可知，本文研究的基于瞬态噪声抑制结合调制域谱减再通过PNCC倒谱距离进行端点检测的算法在测试的四种噪声环境下相对于对比算法检测准确率较高。图14和图15是在平稳噪声环境下的检测结果，由图可知，本文算法在各信噪比条件下均优于对比算法，其中图 15中多带谱减结合倒谱距离在0 dB、f16噪声环境下与本文算法相当。原因是本文检测为平稳噪声，故只采用调制域谱减进行前端增强，根据前面实验可知调制域谱减与多带谱减信噪比提升相差不大，实验结果前后相符。图16和图17表示的是非平稳噪声环境下的结果，从图中很明显可以看出本文算法较对比算法有了大幅度提升，尤其在-10 dB恶劣环境下性能提升约4%～10%，说明算法可改善非平稳噪声干扰。以上实验有效验证了本文算法的抗噪鲁棒性。

图17 不同算法在敲击噪声环境下端点检测正确率比较Fig.17 Accuracy comparison of endpoint detection by different algorithms in tapping noise environment

4.3 本文算法的适用环境和后续研究

非平稳噪声环境下的算法性能是人们关注和研究的重点之一，实验结果表明本文算法适用于处理瞬态冲击噪声环境下的语音，其具有一定的抗噪稳健性，对低信噪比下的端点检测仍然有效。

由于本文算法结合了瞬态噪声抑制、调制域谱减以及PNCC倒谱距离，而PNCC则是在MFCC基础上进行算法改进的，因此本文算法复杂度要比一般的单参数算法稍高，在平稳噪声环境下本文算法与文献[2]、文献[20]均采用了调制域谱减这一相对复杂有效的算法，且不执行瞬态噪声抑制模块，三者的运行时间相当；文献[21]、多带谱减结合倒谱距离这两个算法的耗时相对较少，然而在非平稳噪声环境下本文算法采用的瞬态噪声抑制在确保精确度的同时很难兼顾实时性。文中为了提高算法的实时性，通过对噪声类型的判断决定是否开启瞬态噪声抑制，可在一定程度上优化算法，同时随着后续计算机硬件运算能力的提高，有望能够改善此问题。

因此，如何在保证精确度的前提下优化算法结构，缩短运行时间也是本文后续研究的重点。