融入频域先验信息压缩感知方法的主动声呐回波信号处理

李 季，孙同晶，刘 桐

(杭州电子科技大学通信信息传输与融合技术国防重点学科实验室，浙江杭州310018)

0 引 言

主动声呐信号是认识水下目标的有效途径之一。主动声呐系统有目的发射声波探测目标，经目标反射产生回波信号，通过回波信号来认知目标，但接收到的回波信号数据量大，且有大量的噪声干扰，给声呐系统带来信息传输、采集和存储的巨大压力。

压缩感知方法[1-2]的出现，打破了传统奈奎斯特(Nyquist)采样定理为基础的数字信号处理方法，相比于传统采样，该理论对信号采样的同时对信号进行压缩，利用空间变换来描述信号，在获取压缩观测信号后，通过求解一个非线性优化问题来完成原始信号的恢复，整个过程降低了信号数据的传输和存储成本。压缩感知理论一出现就受到了研究者的广泛关注，在雷达成像[3]、语音信号处理[4]、超声成像[5]、图像压缩[6]等领域都受到了高度关注。在水声信号处理领域，主要包含信号压缩及其重构、水下目标分类识别等。文献[7]基于高斯测量矩阵和正交匹配追踪重构算法，完成了水下信号的压缩和重构；文献[8]基于稀疏分解理论，利用信号的先验信息构建先验稀疏矩阵，进而实现了水下带噪声信号的重构和水下目标的分类识别；文献[9]利用水下回波样本集来构建稀疏字典，实现了水下底质回波的分类。

水下环境复杂，主动声呐的回波信号在携带目标信息的同时，会混入大量噪声干扰，给主动声呐回波信号的处理带来困难。针对低信噪比的水下回波处理问题，本文从待处理信号本身的固有特性及其结构出发，针对主动声呐入射信号能量集中，并非传统意义上的稀疏信号的特点，将其从时域转换到频域，获得更稀疏、幅值特性更加明显的频域先验信息，再结合压缩感知稀疏分解理论，将入射信号的频域先验信息融入稀疏矩阵的构建，使回波信号能更好地完成从高维到低维的稀疏表示。经压缩观测得到观测信号后，结合目标回波的特性，与传统正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)结合，形成基于“块”的正交匹配信号重构算法，完成携带目标信息信号的重构。实验结果表明，无论是仿真信号还是湖上实测数据，相比于传统压缩感知算法，本文提出的融入频域先验信息的压缩感知方法在处理低信噪比的水下信号时，重构精度有较大提升，为进一步分析目标的当前状态和特征提供依据。

1 压缩感知理论

压缩感知理论表明，当某个信号可以用有限稀疏基表示时，采集少量数据作为观测值，通过重构算法就可以完成对原始信号的重构。压缩感知理论主要包括信号稀疏分解、信号测量和信号重构这三个核心部分，理论框架如图1所示。

图1 压缩感知理论框架Fig.1 The framework of compressed sensing theory

1.1 稀疏表示

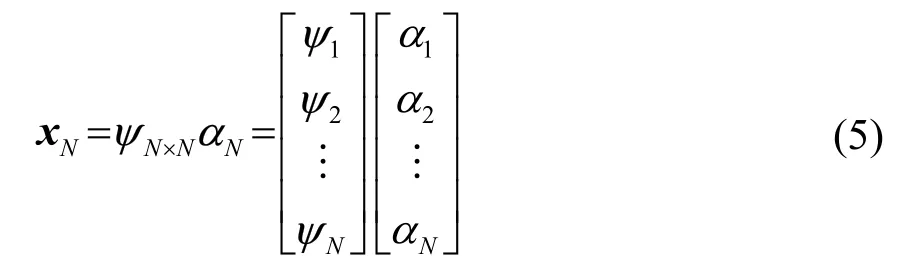
信号的稀疏表示是利用线性逼近的思想，将信号分解为若干个基本信号单元的线性组合来表示。将N维信号x，x ∈ CN×1展开为一组标准正交基线性组合：

式中：Ψ是N× N维的稀疏矩阵，称为信号x的稀疏基；α为稀疏系数。若α中只含有K(K ≪N)个非零系数，则称信号x在稀疏矩阵Ψ下是K稀疏的信号。常见的稀疏矩阵有离散余弦变换矩阵和小波基矩阵。目前，一些学者提出了基于发射信号先验信息的冗余字典下的稀疏分解[10-11]，使其更适用于一般稀疏信号的处理。

1.2 测量矩阵

信号的测量是获取信号低维测量值的重要步骤，测量矩阵要满足等约束性准则(Restricted Isometry Property,RIP)[12]，以保证测量得到的数据在重构信号时，原始信号的信息尽可能地不丢失。通常采用一个与稀疏矩阵Ψ非相关的观测矩阵ΦN×N来完成对待处理信号的压缩观测。对信号x进行压缩观测得到：

这样获取到M个线性观测信号y∈RM，由线性投影得到的少量观测信号y包含了带重构信号的足够信息。

1.3 重构算法

重构算法是由观测的压缩信号实现信号重构的重要途径，算法的设计应该遵循如下基本准则：用少量压缩测量信号的信息，快速、稳定且精确地重构出原始信号。从信号的测量理论可知，由低维观测信号y恢复高维的原始信号x是一个病态方程求解问题，存在无穷多解。将信号稀疏表示与压缩观测相结合起来，观测信号y可以表示为

式中，A=ΦΨ为传感矩阵，是测量矩阵与稀疏矩阵的矩阵相乘。因稀疏系数是K稀疏的，使得信号求解存在可能，将方程的求解转化为一个非线性优化问题，就能从观测信号y、稀疏矩阵Ψ和观测矩阵Φ近乎完整地重构原始信号x。目前，压缩感知重构算法主要包括凸松弛算法[13]、贪婪类匹配追踪算法[14]和组合类算法[15]。

2 融入频域先验信息的压缩感知方法

根据压缩感知理论，在确定观测矩阵的情况下，稀疏信号的处理主要采用稀疏矩阵和重构算法。本文从主动声呐信号的自身特性与结构出发，得到入射信号的频域先验信息，并将其作为原子融入稀疏矩阵的构建，得到频域先验信息的稀疏矩阵。已知水下目标回波信号是入射信号的另一种叠加表示形式，将该特性与OMP算法结合，形成基于“块”的正交匹配查找的重构算法。

2.1 频域先验稀疏分解

水下传播能量衰减慢，声呐系统发射的入射信号在时域上能量相对集中，是时间和幅值的对应。傅里叶变换理论[16-17]指出，对任何波形s(t)都可以用多个正弦函数线性叠加表示，并且每个分量函数都有对应的频率、相位和幅值，通过傅里叶变换求解这些系数，可以完成对信号的简化。

这类在时间上连续、幅值固定的入射信号，通过傅里叶级数展开，可以转换成幅值突出、特征明显的频域稀疏信号。仿真宽带水下回波信号函数s(t)=1·e-i(2πf)，信号频率f=30 kHz，信号脉冲时间T=1 ms，其时域和频域信号波形如图2所示。

图2 仿真信号的时域和频域图Fig.2 The time domain and frequency domain charts of simulated signal

从图2可以看出，对单位时间内的信号而言，入射仿真信号在频域具有更好的稀疏特性，其幅值特征也更加突出。

一般稀疏信号通常选取离散余弦矩阵(Discrete Cosine Transform,DCT)对信号进行高维投影。水下环境复杂，存在大量的噪声干扰。因此结合信号的固有特性，采用频域先验信息构建过完备原子库作为稀疏矩阵。首先假设入射信号和回波信号的采样速率满足奈奎斯特采样定理，采样周期为Ts，脉冲宽度为τ，一个脉冲宽度的样本点数为 n，产生的总样本点数为N。得到入射信号的频域信息后进行能量归一化处理。得到原型原子 G =[g1g2…gn]，将其看作为一个原子块，对原子块位移，取不同的起始点构成过完备原子库(稀疏矩阵)[18]。具体表达式如下：

由上述可知，由原子块形成的稀疏基具有相同的特征信息，每个稀疏基里最核心的原子块与入射信号的频域先验信息维持一致，两个稀疏基之间的区别是有效原子块的位置不同，可通过相互平移得到。针对低信噪比的声呐目标回波信号的处理，融入频域先验信息构成的稀疏矩阵如图3所示。

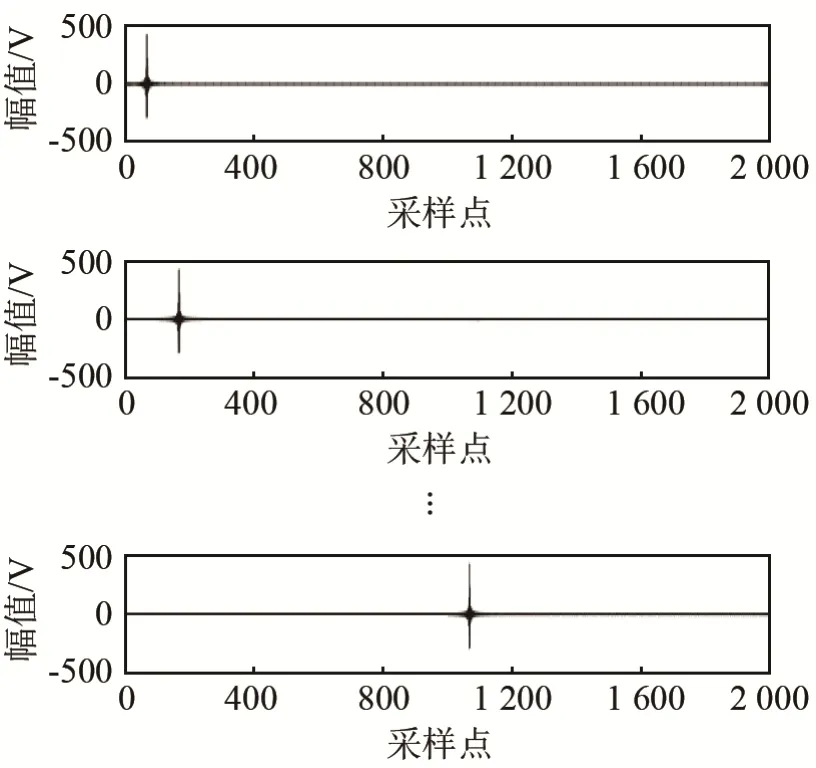
图3 融入频域先验信息的稀疏矩阵图Fig.3 Sparse matrix with prior information in frequency domain

从图3中看出，每一个稀疏基ψi都包含入射信号的先验信息，各个原子的非零区域特征一致，且与发射信号的频域波形一样。根据水下稀疏分解原理，水下目标回波信号的稀疏分解矩阵运算如式(9)所示：

式中：长为N的水下目标回波信号可以由M个先验信息原子与M个稀疏系数的乘积线性叠加表示：

这样，回波信号的重构问题就可以转换为稀疏系数的求解问题。

2.2 频域先验重构算法

频域先验重构算法是基于 OMP重构算法。OMP算法原理简单、计算快速的特点使其具有广泛的应用。但OMP算法的计算是基于点对点的全局匹配查找，每一次查找都需找出最相关的原子，循环迭代直到信号重构完成。整个过程中没有考虑到待处理信号的特点。针对目标回波信号，基于正交匹配追踪方法，将其块稀疏特性融入到重构算法中，实现由单点匹配到成块匹配。因此，提出一种频域先验的正交匹配追踪(Frequency Priori Orthogonal Matching Pursuit,FPOMP)算法，从构建的频域先验稀疏矩阵原子库中选择与水下目标回波信号匹配度最高的原子，再用回波信号减去其在原子库中的投影，得到残差信号。将残差代入循环，继续迭代从原子库中选择与其最相关的先验原子，当残差小于给定阈值时停止迭代。

与传统的正交匹配追踪算法相比，FPOMP算法每次迭代匹配到的都是包含发射信号先验信息的原子块，而不是一个信号采样点。通过有限几次迭代就能重构恢复出水下目标的回波信号。FPOMP重构算法具体步骤如下：

(1)初始化。对残差初始化 r0=y，原子的索引集合I为空集，重构原子集合H为空集，稀疏分解系数α=0，迭代次数k=0。

(2)原子块的选择。计算残差信号与稀疏矩阵中每个原子块的内积：

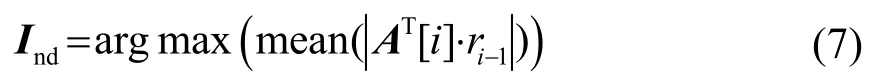
式中：i∈[1,N]，mean()表示求均值，A为传感矩阵。找出内积向量中绝对值最大的原子块ψi，将其对应的索引Ind加入原子的索引集合I中，将上述原子块ψi加入重构原子集合H。

(3)更新残差信号 ri=ri-1-ψiαi，稀疏分解系数α(i)=αi，ri为第k次更新的残差。

(4)如果不满足迭代终止条件，则迭代次数 k加 1，继续执行；若满足终止条件，则停止迭代，得到稀疏系数集合与重构原子集合。

(5)将重构原子集合与稀疏分解系数集合对应进行线性叠加运算，得到水下目标回波信号的频域重构信号，再通过逆运算得到时域信号，进而完成信号的重构。

FPOMP算法与传统的压缩感知方法比较，迭代时的最大相关性计算，残差更新，每次得到的是包含频域先验信息的原子ψ，少量次数迭代就可得到频域信息支撑集，最后通过伪逆运算即可完成信号重构。FPOMP算法的具体流程如图4所示。

图4 FPOMP算法的流程图Fig.4 Flow chart of FPOMP algorithm

3 算法性能验证

为了验证本文提出的基于频域先验信息的压缩感知方法的性能，先基于仿真回波信号进行处理以验证方法正确性。然后通过主动声呐发射接收装置，获取湖上实测数据并处理，证明本文方法实际应用的可行性。

本文以信号匹配率作为信号重构的评判标准，匹配率定义：以入射信号与重构信号的绝对值之和的二范数减去两者绝对值之差的二范数，再比上两者绝对值之和的二范数。匹配率的计算公式为

3.1 仿真信号性能验证

水下回波信号往往含有大量噪声干扰。仿真信号为干净信号，因此，加入高斯白噪声，以信噪比(Signal Noise Ratio,SNR)为指标，信噪比越低，噪声干扰越大，处理起来就越困难。

为了验证本文方法的抗噪性能，加入不同大小的高斯白噪声。首先，采用高斯测量矩阵从原始信号中提取出少量数据，然后分别采用本文方法和传统压缩方法进行重构。传统压缩感知方法采用离散余弦变换稀疏矩阵、高斯测量矩阵和正交匹配追踪重构算法进行信号重构。图5(a)～5(d)是在仿真信号压缩比为50%、信噪比分别为3、0、-3、-5 dB时的重构结果图。

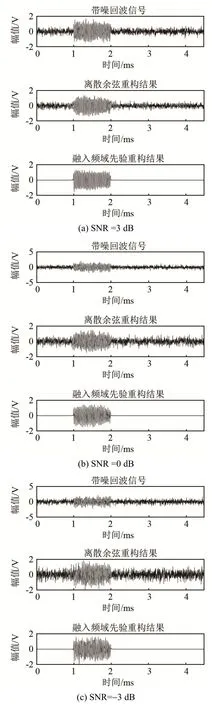
图5 不同信噪比仿真信号的处理结果Fig.5 Processing results of simulation signals with different SNR

从图5中可以看出，在信号的压缩为50%，信噪比大于0 dB时，传统方法基本能恢复信号，但重构回波中含有噪声，而基于频域先验方法的重构效果较好；当混入的噪声增加，信噪比为-3 dB时，从图5(c)可以看到，传统压缩感知方法难以分辨带目标回波信号的位置，而基于频域先验信息的压缩感知方法的信号重构效果明显；当信噪比进一步降低，本文方法依旧可以重构出声呐回波信号。实验结果验证了CSFPI方法在处理含噪声回波信号的可行性。

3.2 湖上实测数据获取

该试验测试目标是潜艇缩比模型(BeTSSi-Sub)，测试布放方法如图 6所示。有两个布放和旋转设备，距离为20 m，一个用于布放收发合置换能器，布放深度是水下10 m，另一个用于布放和旋转目标，布放深度也是水下10 m。为了获得不同入射角的回波信号，潜艇模型逆时针匀速旋转。

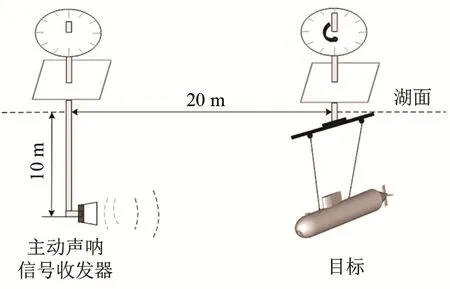
图6 湖上实验的布设Fig.6 Layout of lake trial

采用线性调频信号作为入射信号，入射信号形式为f(x)=A ej(2πft+πKt2)，其中，信号幅值A=1，信号频率 f=60 kHz，信号带宽 B=40 KHz，信号脉冲长度T=1 ms，信号调频斜率K=B/T。在测试中，目标以逆时针方向匀速旋转，通过这种方式获得了不同入射角的回波信号。从这些回波信号中，选取了入射角为30°和90°的回波信号，信号波形如图7所示。

3.3 水下目标回波信号性能验证

对实测的目标回波信号处理，取压缩比50%，加入高斯白噪声，信噪比分别为3、0、-3、-5 dB，采用频域先验压缩感知方法和传统方法进行处理。图8(a)～8(d)是入射角为30°的回波信号处理对比结果图。图 9(a)～9(d)是入射角为 90°的回波信号的重构结果图。

从实验结果来看，无论主动声呐回波信号的入射角度为 30°还是 90°，当压缩比为 50%，且 SNR为3 dB时，传统压缩方法仅能探测出回波位置，而本文提出的CSFPI方法能够完整地滤掉噪声，并重构出水下目标的回波信号。随着噪声干扰不断增加，SNR为0 dB时，传统压缩方法已经完全不能适用于湖上实测数据的重构，但是CSFPI方法依旧可以重构出信号大部分信息。当SNR为-5 dB时，噪声干扰完全淹没了目标回波信号，CSFPI算法仍然能探测出携带目标信息回波的位置，并重构出部分目标回波信号。

从信号重构的指标——匹配率进行分析，两种方法不同信噪比重构信号的匹配率如表1所示。从表1中可以看出，当噪声较小时，CSFPI方法重构信号的匹配率能达到90%，传统压缩感知方法的匹配率为60%左右。随着噪声的不断增加，CSFPI方法匹配率仍然能达到83%以上，而传统方法匹配率低于50%。当信噪比为-5 dB时，噪声完全淹没了携带目标信息的回波信号，CSFPI方法的匹配率仍可达到70%以上，充分展示了CSFPI方法在处理低信噪比声呐回波信号时的性能。

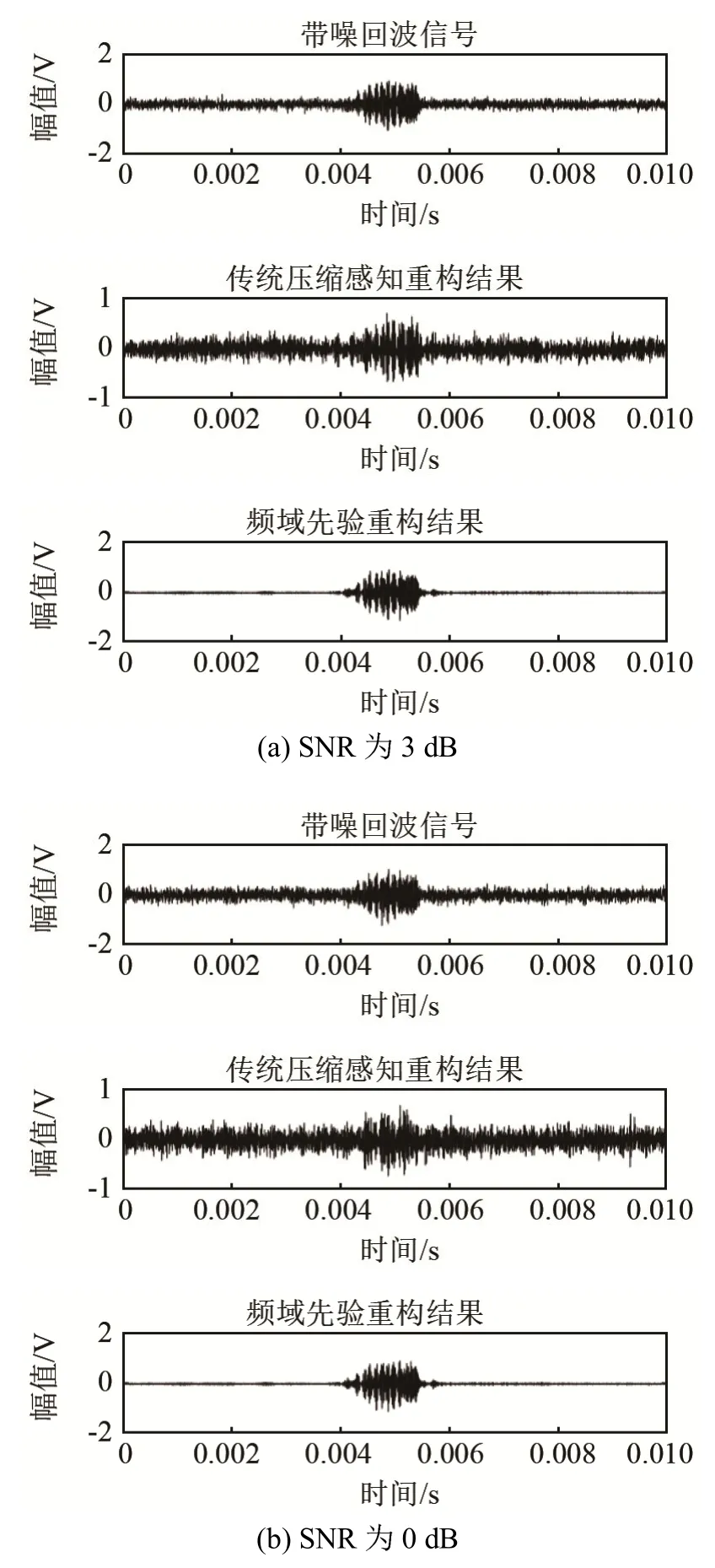
图9 不同方法对90°回波信号在不同信噪比下的处理结果Fig.9 Processing results of 90° echo signal by different methods under different SNRs

表1 传统方法和CSFPI方法在不同信噪比下重构信号的匹配率对比Table 1 Comparison of matching rates of reconstructed signal by traditional and CSFPI methods under different SNRs

4 结 论

本文针对水下声呐目标回波信号噪声干扰较大时难以处理的问题，提出了融入频域先验信息的压缩感知方法。从待处理回波信号本身的固有特性和结构出发，将其从时域转换到频域，得到更加稀疏和幅值特征更加明显的频域信号，将其看成一个原子并融入稀疏矩阵，构建过完备原子库，与传统的贪婪迭代算法结合，对压缩观测到的信号进行重构。对仿真信号和湖上实测数据进行处理和分析，与传统压缩感知方法进行对比。结果表明，当信噪比低于-3 dB时，传统压缩感知方法的匹配率小于50%，不能滤掉噪声重构出回波信号；而经过CSFPI方法处理的重构信号匹配率大于70%，信号的重构效果明显，表明 CSFPI方法在处理含有大量噪声的水下目标回波信号时具有明显的优势。