基于鸡群算法的近场声源三维定位MUSIC算法

邵 元，杨 超，郭 辉

(上海工程技术大学 机械与汽车工程学院，上海201600)

0 引 言

多重信号分类(Multiple Signal Classification,MUSIC)算法是空间谱估计中的一种超分辨估计算法，常用于远场信号的波达方向估计[1-2]。当声源位于近场时，距离将是一个不可忽略的参数[3]，并且传统MUSIC算法失效。基于近场信号模型的MUSIC算法[4-5]可以估计近场声源的三维位置，但网格搜索带来的巨大计算量是限制算法应用的主要因素[6]，运算时间过长使其难以在工程中得到应用。

为了提升算法的实时性、减少算法的计算量，研究人员使用近几年兴起的群群智能优化算法代替传统的网格搜索模式[7]。目前，粒子群优化[8]、遗传[9]等算法已经应用于远场波达方向估计。该类算法虽然减小了计算量，但依然存在收敛速度慢等缺点。鸡群算法是一种通过模仿鸡群觅食行为而提出来的群智能优化算法[10]。相较于其他群智能优化算法，鸡群优化(Chicken Swarm Optimization,CSO)在函数求极值问题上具有更优秀的性能[11-12]。本文融合快速寻优的鸡群算法和近场三维MUSIC算法，提出了一种快速近场声源位置估计算法。近场声源定位的仿真表明：本算法具有定位精度高、计算速度快、实时性强等特点。

1 近场信号模型和鸡群算法

1.1 近场信号模型

根据声源与传声器阵列的距离，信号传播模型可分为近场模型和远场模型。判断近场的公式为

其中：L为麦克风阵列中心与声源位置的直线距离；D为阵列孔径；λ为信号波长。声源位于近场时采用球面波模型要比传统远场平面波模型更加精确。这是因为近场环境下，阵元接收到的信号不仅有相位的差异，幅度差异也十分显著。

假设K个近场窄带信号辐射到由M个麦克风组成的阵列上，第i个麦克风接收到的信号表达式为

其中：i=1,2,··,M ，j=1,2,··,K ，ni(t)表示第i个麦克风在t时刻接收到的高斯白噪声。整个麦克风阵列的接收信号表达式为

式中：rij代表第i个声源与第j个阵元的距离；ωc为声源的中心角频率；τij为第i个麦克风接收到第j个信号的时间延迟因子，其表达式为

麦克风阵列近场接收信号示意图如图1所示。声源的位置矢量分别为 s1,s2,··sK，阵列中麦克风的位置矢量分别为p1,p2,··pM，c为声波波速。

图1 麦克风阵列近场接收信号示意图Fig.1 Schematic diagram of receiving signal in the near-field of microphone array

1.2 鸡群算法

Meng[10]参考鸡群觅食行为解决优化问题。鸡群算法具有以下前提：

(1)鸡群由多个子群构成，每个子群包含一个公鸡、一些母鸡和小鸡；

(2)鸡群中适应度值最高的为公鸡，其次为母鸡，再次为小鸡。每个子群必包含一个公鸡，母鸡搜寻食物随机跟随公鸡，小鸡搜寻食物随机跟随母鸡，公鸡作为首领带领子群搜寻食物；

(3)迭代后，根据适应度值重新排序并重新定义公鸡、母鸡和小鸡。

满足上述理想化规则后，公鸡的位置更新公式为

式中：ε为大于0的极小值；fi为第i只公鸡的适应度值；fk为从种群中随机选取的第k只公鸡的适应度值；k∈[1,N]，k≠i。

母鸡的位置更新公式为

小鸡的位置更新公式为

2 基于鸡群算法的近场三维MUSIC

设F(t)的相关矩阵为R，则：

RSS(t)=E［S(t)SH(t)］，σ是高斯白噪声的功率。对式(12)进行特征分解并排序得到：

其中：[λ1··λDλD+1··λM]是R(t)的特征值，U是对应的特征向量组成的矩阵。并根据特征值大小将U分解为两个空间：信号子空间和噪声子空间，根据子空间理论：

定义空间谱函数为

传统MUSIC算法将对空间谱函数进行网格搜索，进而输出使空间谱函数为极大值时的 θ 、φ、r，即空间源信号的俯仰角、方位角和距离。网格搜索虽然可以有效精确地得出结果，但搜索运算速度慢，计算量大。为了解决该问题，本文采用鸡群优化算法替代传统网格搜索。基于鸡群算法的近场声定位三维MUSIC算法的步骤如下：

(1)初始化参数。将空间谱函数定义为计算适应度的目标函数，具体参数设置如表1所示。

(2)初始化种群并计算n个个体的适应度。

(3)如满足迭代次数与种群更新间隔代数G的比值为 1，则按照适应度值对鸡群个体排序，确定鸡群的等级制度。与此同时将鸡群分为多个子群，并随机分配母鸡和小鸡。

(4)更新公鸡、母鸡和小鸡的位置。

(5)以适应度值为指标再次计算各个鸡群个体的适应度值，并且更新个体最优和全局最优。

(6)如果达到最大迭代次数，转步骤(7)；反之返回步骤(3)继续循环迭代。

(7)输出全局最优值即声源的位置坐标。

表1 算法初始参数Table 1 Initial parameters of the proposed algorithm

3 仿真与结果

3.1 仿真设计

本文算法的目的是在提升近场声源定位精度的同时，降低算法的运算时间。首先对本文算法和三维MUSIC算法的定位结果进行了对比分析。其次对本文算法和三维MUSIC算法进行了均方根误差分析，分别得到了俯仰角、方位角和距离的均方根误差(Root Mean Squared Error,RMSE)曲线。最后对本文算法和三维MUSIC算法的计算量和运算时间进行了对比分析。

麦克风阵列拓扑图如图2所示。仿真采用了36个麦克风组成的同心圆面阵列。在高斯白噪声背景下，选择两个频率分别为1 800、2 000 Hz的非相干正弦信号作为信号源，快拍数为 500，参数设置见表1。

图2 麦克风阵列拓扑图Fig.2 Layout of microphone array

3.2 仿真分析

3.2.1 定位性能分析

图3 直角坐标系中的真实声源位置和算法定位结果Fig.3 Actual sound source position and the localization results of the algorithm in Cartesian coordinate system

图3和表2比较了信噪比为15 dB时，真实声源位置和本文算法定位结果。图3中，空心圆为麦克风阵列，实心圆表示声源实际位置，三角形表示本文算法估计结果。x、y和z方向的误差为0.025、0.025和0.035 cm，可以看出真实声源位置和本文算法定位结果在空间中几乎重叠，这说明本文算法可以对近场声源进行准确的三维位置估计。

表2 声源实际位置和算法定位结果对比Table 2 Comparison of actual sound source position and the localization results of the algorithm

3.2.2 均方根误差分析

本文算法计算过程中采用极坐标系，声源位置的俯仰角、方位角和距离随着 SNR变化的均方根误差曲线如图4所示。其中三维MUSIC算法的搜索步长为1°和1 cm。随着SNR的增加，RMSE越来越小这是因为MUSIC算法中噪声子空间和信号子空间的分离更加彻底。本文算法的定位精度要高于三维MUSIC算法，这是因为本文算法采取有限次不停迭代寻优的方式，随着迭代次数的增加，寻优结果更加精确。而三维MUSIC算法理论上可达到很高的精度，但精度受限于搜索步长，搜索步长对于计算量和计算时间的影响是巨大的，三维MUSIC算法的搜索步长为1°和1 cm，计算时间约为35 s，当搜索步长为0.1°和0.1 cm的时候，计算时间为4 h左右。从图4可以看出，在可接受的运算量和运算时间内，本文算法比传统近场三维MUSIC算法近场声源位置估计的精度高。

图4 不同信噪比下的定位均方根误差曲线(蓝色：三维MUSIC算法；红色：本文算法)Fig.4 RMS error curves of localization under different SNR(blue for 3D MUSIC algorithm,red for the algorithm proposed in this paper)

3.2.3 计算时间分析

表3对比了本文算法和三维MUSIC算法的运算时间和时间复杂度。其中运算时间是 SNR为15 dB条件下、50次仿真结果的平均值。

仿真时本文算法所花费的计算时间仅为三维MUSIC算法的1.9%，这说明本文使用鸡群算法替代网格搜索的方式可以在保证定位精度的前提下，极大地降低运算量，提升运算速度。

表3 两种方法的运算时间和复杂度对比Table 3 Comparison of operation time of the two methods

4 实验验证

4.1 实验设计

实验系统由测量、分析处理和结果显示部分组成。测量部分由均匀同心圆麦克风阵列和多通道信号采集系统组成；分析处理部分由本文算法组成；笔记本电脑完成结果显示部分。实验地点是半消声室，麦克风阵列离地面间距为 50 cm。参数设定见表1与表4。实验设备及声源的空间位置分别如图5、6所示。

表4 实验系统参数Table 4 Parameters of the experimental system

图5 实验设备Fig.5 Experiment apparatus

图6 声源的空间位置Fig.6 Spatial locations of sound sources

4.2 实验分析

4.2.1 定位性能分析

表5和图7比较了空间中实验声源位置和算法定位结果。图7中实心圆表示实际位置，三角形表示本文算法估计结果。由此可见，本文算法在实际应用中可以对近场声源进行准确的三维位置估计。

表5 声源的实际位置及其定位结果Table 5 Actual locations of two sound sources and their localization results

图7 声源实际位置及其定位结果的对比图Fig.7 Contrast map between actual locations of two sound sources and their localization results

4.2.2 均方根误差分析

图8为三维MUSIC算法和本文算法随着SNR变化的均方根误差曲线，其中三维MUSIC算法的搜索步长为1°和1 cm。从图8可以看出，在实际应用中两个算法的精度均有所下降，但本文算法保持着高精度的同时依然比传统三维MUSIC算法的定位精度高。

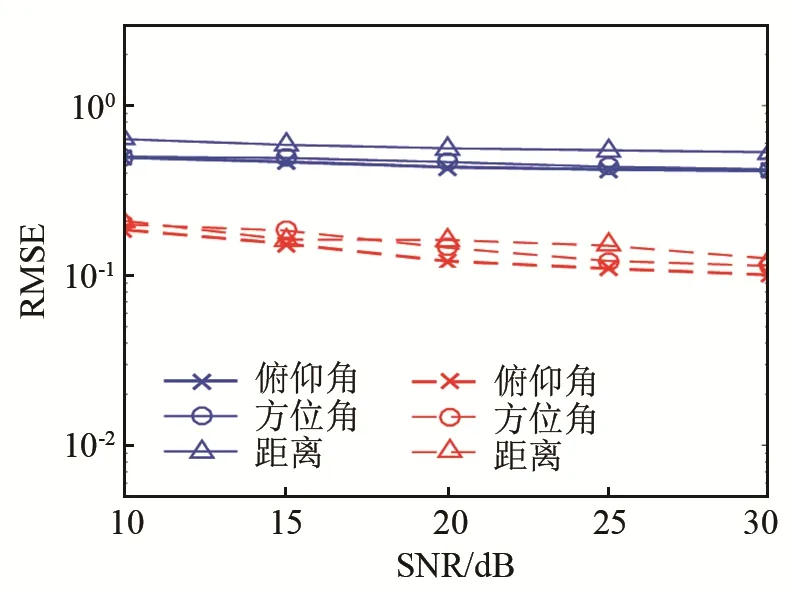
图8 不同算法定位均方根误差曲线(蓝色：三维MUSIC算法；红色：本文算法)Fig.8 Root mean square error curves of localization by different algorithms(blue for 3D MUSIC algorithm,red for the algorithm proposed in this paper)

4.2.3 计算时间分析

实验对比了本文算法和三维MUSIC算法的运算时间，结果如表6所示。其中运算时间为20次实验结果的平均值。在实验条件下本文算法所花费的计算时间仅为三维MUSIC算法的3.2%，这说明在实验中本文算法在保证定位精度的前提下具有极好的实时性能。

表6 运算时间对比Table 6 Comparison of operation time

5 结 论

针对近场三维定位MUSIC算法存在计算量大、实时性差的缺点，本文提出了一种基于鸡群算法的三维MUSIC近场声源定位算法。本文算法使用鸡群算法替代网格搜索来进行寻优，提升了定位精度且大大降低了计算量和运算时间。仿真和实验结果表明：对于稳态声源，本文算法的定位精度更高，抗噪能力强，且计算速度更快。本文算法的提出有利于声源三维定位技术的推广于应用，未来将对瞬态声源的定位效果进行探究。