水下多孔吸声材料夹层板隔声分析

黄梦情，陈美霞

(华中科技大学船舶与海洋工程学院，湖北武汉430074)

0 引 言

相对于传统的双板空腔[1-2]结构，添加多孔弹性吸声材料的夹层板结构[3]在空气中具有更优良的声学性能。

国内外有很多关于多孔吸声材料的研究。早期著名的Biot理论[4]详细阐述了声波在多孔吸声材料中的传播。随后，基于Biot理论，Bolton等[3]分析了带多孔吸声材料的多层板的隔声性能，详细地推导了多孔材料中三种声波的表达式，并用实验数据对最后的理论结果进行了验证。同样基于Biot理论和Bolton的多层板理论，Liu[5]推导了带多孔吸声材料的三层板的隔声量(Sound Transmission Loss,STL)理论计算公式，分析、对比了三层夹层板和双层夹层板的隔声性能差异，并分析了三层夹层板取代双层夹层板的可能性。针对静态的流体，Zhou等[6]分析了在一侧存在均匀流情况下的双层带吸声材料夹层板的隔声性能，剖析了外部均匀流对夹层板隔声性能的影响。与此同时，Shen等[7]和Liu等[8]分别研究了外部均匀流对四边固支边界并带多孔吸声材料双板的隔声性能的影响。

早期，国内的陈卫松等[9]也推导了多孔弹性材料三层夹层板的隔声量计算公式，并将其计算结果与双板结构进行对比分析。白聪等[10]详细分析了三聚氰胺芯层和通常的聚氨酯芯层隔声性能的差别，阐述了三聚氰胺芯层的吸声优势。宁景锋等[11]分析了孔隙率、层厚和流阻率对含空气背衬层的分层多孔材料吸声性能的影响。朱从云等[12]采用声电类比的方法从理论上求解多层吸声材料的吸声系数，并与试验结果进行对比。

有不少学者都对多孔吸声材料夹层板的隔声性能进行了研究，但他们分析的模型大多处于空气中。对于水下的动力结构，其动力区域的隔声性能是水下工程中非常重要的部分。减小河流或海洋噪声污染也是当前工程领域中比较关心的问题。因此，本文主要讨论水下多孔吸声材料夹层板的隔声性能，并与空气中的结构进行对比，同时分析了多孔吸声材料厚度和空腔空气层厚度对结构隔声的影响。

1 模型隔声理论分析

模型隔声理论分析主要包括：夹层板理论分析、多孔弹性吸声材料的传声理论、夹层板的边界条件以及最后模型的隔声量求解。夹层板理论和多孔吸声材料传声理论为模型提供理论基础，再结合边界条件，即可求解出相应模型最后的隔声量。

1.1 夹层板理论模型

本节主要介绍三种水下多孔吸声材料夹层板理论模型，包括BB型、BU型和UU型。3种模型的基本示意图如图1所示。

图1 多孔吸声材料夹层板模型示意图Fig.1 Schematic diagram of three models(BB,BU and UU)for the sandwich plate with poroelastic material

在图1中，夹层板左右两侧均为铝板，中间实体部分为多孔吸声材料。在夹层板左侧施加入射声波，穿透夹层板结构，得到右侧的辐射声波。

单位振幅的简谐平面波入射到夹层板时，入射声波的速度势函数可表示为

式中：kx=ksinθ，ky=kcosθ，k=ω/c。其中，θ为声波的入射角；I0为速度势幅值。

入射域中的声波主要包含入射声波和反射声波，其总声波速度势函数可表示为

在多孔吸声材料与面板之间的空腔域中，声波主要包含透射声波和反射声波，其声波的总速度势函数可表示为(指数项前变量均为函数的系数幅值，仅表示大小，无实际含义，下同)：

辐射域中仅包含辐射声波，其声波速度势函数表示为

左右双板的横向振动位移为

双板的纵向位移为

在夹层板结构中，双板中的结构波和流体域中的声波在x方向上的波数相等：

式(8)中的波数分量具体表达式为

结合式(9)，波数关系式(8)可化简为

其中：ki=ω/ci、ka=ω/cd、kr=ω/cr。入射域、空腔域和辐射域中的密度和声速分别表示为(ρi,ci)、(ρd,cd)和(ρr,cr)。夹层板模型两侧为水，中间为空气。将式(10)进行转化，可得声波入射极限角：

其中：ci=1 500 m·s-1，cd=343 m·s-1。式(11)表明：当声波入射角为0°～90°时，透射域中均有透射声波存在，即不存在声波入射极限角的限制。

通过上述理论推导，双板的位移和各个流体域中的声波速度势均可被完整地表达。

1.2 多孔弹性吸声材料的传声理论

本小节分析声波在多孔弹性吸声材料中的传播。根据Biot理论和Bolton的多层板理论，多孔吸声材料的固体骨架的位移分量ux、uy和流体介质的位移分量ux、uy为

法向(y向)的固体骨架应力σy、介质流体应力s和x-y平面的剪切应力τxy分别表示为

在式(12)、(13)中，b1、b2和g分别表示为

式(14)中，各个密度的具体表达式为

式中：ρ1、ρ2和ρa分别表示为固体骨架密度、流体相密度以及二者的耦合密度。

流体相密度ρ2和耦合密度ρa可表示为

式(16)中，ρ0表示多孔材料中流体介质的密度；h和ε′分别表示介质的空隙率和几何结构因数。

在(15)式中，b表示粘性耦合系数：

在式(14)中，P表示多孔材料的弹性因数：

式中：A表示第一拉梅常数，N表示弹性剪切模量，二者的具体表达式为

式中：E1和υ分别表示为固相的杨氏模量和泊松比。复数杨氏模量E1为：E1=Em(1 + j η)，Em表示静态的杨氏模量，η表示损耗因子。

在式(13)、(14)中，系数Q和R分别表示在固体骨架和间隙流体体积改变下的弹性耦合系数：

式中：E2表示孔隙中流体体积模量。在本模型中，多孔材料的间隙流体为空气(密度ρ0，声速c0)。同时，假设多孔材料中气孔为圆柱形孔，此时气孔中空气的体积模量E2及其相关中间变量可表示为

式中：γ表示定压比热和定容比热之比；Ji表示i阶第1类Bessel函数；Pr表示普朗特常数；σ表示流体的宏观静态流阻。

在式(12)和式(13)中，两种纵波和一种剪切横波的波数关系表示为

在式(23)中，系数1A和A2分别表示为

纵波和剪切波在y方向上的分量表示为

1.3 夹层板模型的边界条件

在本文的BB型、BU型和UU型模型中，大致可归类出3种边界条件：

第一种边界条件：多孔吸声材料通过空气层与板连接，如图2所示。相应的边界条件为

式中：(p1,p2)和(v1y,v2y)分别表示面板两侧的声压和流体质点振动速度。声压p和vy的具体表达式为

图2 边界条件1：多孔吸声材料与板间接耦合Fig.2 BC(boundary condition)1:indirect coupling between poroelastic material and plate

第二种边界条件：多孔材料两侧均为空气介质，如图3所示。相应的边界条件表达式为

第三种边界条件：多孔材料一侧与板紧密接触，另一侧与空气介质接触，如图4所示。相应的边界条件为

图3 边界条件2：多孔弹性材料的两侧均为空气Fig.3 BC 2:both sides of poroelasstc material are air

图4 边界条件3：多孔弹性材料一侧与板接触另一侧与空气接触Fig.4 BC 3:one side of poroelastic material is in contact with plate and the other side is in contact with air

在式(29)中，hp表示板厚，D和Dp分别表示板的弯曲刚度和纵向刚度，ms表示板的面密度，qp=-σy-s表示多孔材料反作用于板上的法向应力。在式(29)的5和6边界条件中，上标和下标(正负符号)分别表示多孔吸声材料在板面y轴方向的正向和负向。

1.4 夹层板模型的隔声量求解

根据1.3节的阐述，本节列出三个模型理论隔声量求解的边界条件。

不考虑板厚的影响，BB型填充双板：边界条件y=0和y=L。

在y=0处，BB型填充双板的边界条件：

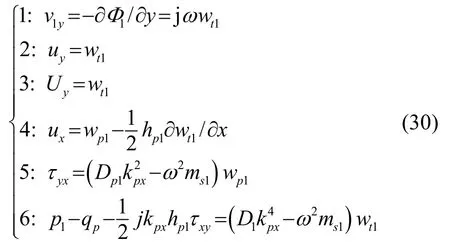
在y=L处，BB型填充双板的边界条件：

BU型填充双板：边界条件y=0、y=L和y=L+δ。

在y=0处，BU型填充双板的边界条件：

在y=L处，BU型填充双板的边界条件：

在y=L+δ处，BU型填充双板的边界条件：

UU型填充双板：边界条件y=0、y=δ1、y=L+δ1和y=L+δ1+δ2。

在y=0处，UU型填充双板的边界条件：

在y=δ1处，UU型填充双板的边界条件：

在y=L+δ1处，UU型填充双板的边界条件：

在y=L+δ1+ δ2处，UU型填充双板的边界条件：

在3种结构的边界条件中，τxy和τyx相等，弯曲刚度(D1,D2)和纵向刚度(Dp1,Dp2)的具体表达式为

最后，夹层板理论模型的声强透射系数为

对于混响入射声场，入射声波的入射积分角取为0°～72°[3]。混响入射声场的平均声强透射系数可表示为[5]

对于混响声场的平均声强积分，本文采用辛普生分步积分，步长选取为2°。最后的隔声量计算表达式为

2 夹层板模型的隔声量验证及分析

2.1 隔声量数值验证

水流体和中间芯材对面板的作用分别由边界条件单独添加，且它们属于不同类型的边界条件。参考本文第1.4节中模型边界条件的具体表达式，水流体对面板的作用属于外边界；中间芯材对面板的作用属于内边界。内边界和外边界通过面板间接联系，不存在直接的相互作用，故可分别进行验证。同时，对水流体这种外边界的处理方式，主要参考Lu等[14]学者的板壳声振耦合的外部流场处理方式；中间芯材这种内边界的处理方式主要参考 Bolton等[3]和陈卫松[9]等学者的处理方式。根据本文结构的特点，分别对水流体和中间芯材进行处理，将模型隔声量结果验证分解为两步：(1)验证水下不含芯材双板的隔声量结果；(2)验证空气中含芯材的夹层板的隔声量计算结果。

将夹层板中芯材去掉，整个模型可退化为水下双板结构，便可与已知方法的计算结果进行对比。双板采用铝板结构，密度ρp=2 700 kg·m-3，泊松比υp=0.33，损耗因子η=0.01，弹性模量Ep=70 GPa，板厚hp=0.001 27 m，空腔高度H=0.015 m。水的密度为ρw=1 000 kg·m-3，声速cw=1 500 kg·m-3；空气的密度ρd=1.21 kg·m-3，声速cd=343 kg·m-3。退化模型的外向两侧流体均为水，中间腔内为空气。在声波垂直入射的情况下，可得到两种方法的计算结果对比图，结果如图5所示。

图5中的结果表明：本文方法退化出的水下双板隔声量理论计算结果与波传递法的计算结果吻合。本文方法能求解水下双板结构的隔声量问题。

图5 两种方法计算的退化水下双板隔声量对比图Fig.5 Comparison of STL of degraded underwater double-panel calculated by two different methods

当夹层板模型两侧的流体为空气时，将本文的方法进行退化，并对比已有的文献结果，验证空气中本模型计算结果的正确性。多孔弹性吸声材料的相关参数为：固体骨架密度ρ1=30 kg·m-3，固体骨架静态弹性模量Em=8×105Pa，固体骨架泊松比υ=0.4，损耗因子 η=0.265，流阻 σ=25 000 N·m-4，几何结构因子ε′=7 .8，介质空隙率 h=0.9。左右面板均采用铝材料，入射板板厚为hp1=1.27 mm，辐射板板厚为hp2=0.762 mm，多孔吸声材料厚度为L=27 mm。BU型结构中间空腔厚度为 δ=14 mm，UU型结构的前、后空腔厚度分别为2 mm和6 mm。入射声波的入射积分角为0o～72o。3种方法计算的3种夹层板模型的隔声量对比(空气中)如图6所示。

在图6中，本文方法计算出的结果与Liu[5]的理论结果吻合，且与Bolton等[3]的试验结果一致，故采用本文方法可解决空气中夹层板的隔声量问题。

结合上述两个隔声量验证结论，表明本文方法能够计算水下夹层板的理论隔声量。

2.2 水下三种结构隔声量对比

计算水下BB型、BU型和UU型3种夹层板结构的隔声量，分析对比出隔声性能较优的多孔吸声材料夹层板结构。

3种模型左、右双板的参数一致，入射板板厚为hp1=1.2 mm，辐射板板厚为hp2=0.8 mm。3种模型中多孔弹性吸声材料的厚度为L=27 mm。在BU型模型中，中间空腔厚度为δ=14 mm。在UU型模型中，中间空腔厚度为δ1=δ2=7 mm。分别计算水下3种模型在混响声波入射情况下的理论隔声量，结果如图7所示。

图6 3种方法计算的3种夹层板模型的隔声量对比图(空气中)Fig.6 Comparison of STL of three sandwich plate models(in air)by three different methods

在水中，BU型和UU型夹层板结构的隔声量远大于BB型。在低频阶段，芯材和辐射板之间的空气层对结构隔声性能起了很关键的作用。通过对比BU型和UU型的隔声曲线，可得出：在低频阶段，芯材与辐射板之间的空气层对隔声影响很大，入射板与芯材之间的空气层基本不影响隔声量；当进入中高频阶段，UU型的隔声性能逐渐优于 BU型，也即表明：此时入射板和芯材之间的空气层对隔声量产生了比较大的影响。

图7 水中3种模型隔声量对比图Fig.7 STL curves of underwater three models(BB,BU and UU)

3条隔声量曲线的对比表明：在水中，UU型的总体隔声性能优于BU型和BB型，其中BB型的隔声性能最差。

2.3 BU型和UU型与双板结构隔声量对比

对比BU型、UU型以及普通双板结构的隔声量，详细分析多孔弹性吸声材料的隔声性能。

BU型、UU型和普通双板结构中的左右双板均采用铝材，入射板板厚为hp1=1.2 mm，辐射板板厚为hp2=0.8 mm。BU型和UU型模型中多孔弹性吸声材料的厚度为L=28 mm。在BU型模型中，中间空腔厚度为δ=14 mm。在UU型模型中，中间空腔厚度为δ1=δ2=7 mm。普通双板中空腔的厚度为δ=42 mm。当入射域为声波混响场时，计算这3种模型在水下的理论隔声量，结果如图8所示。

图8 水下BU型、UU型和普通双板模型隔声量对比图Fig.8 STL curves of underwater three models(BU,UU and double-panel)

在低频阶段，普通双板结构的隔声量略低于BU型和UU型。频率在1～3 kHz之间，BU型和UU型结构存在一个结构的共振隔声低谷，隔声量低于普通双板结构。随着分析频率的增大，普通双板结构出现空腔共振低谷，其隔声性能要低于 BU型和UU型结构。同时，当分析频率高于2 kHz时，UU型结构表现出较优的隔声性能，其隔声量高于BU型和普通双板结构。多孔吸声材料能有效地避免结构空腔驻波共振频率的出现。此外，多孔吸声材料对结构低频阶段的隔声性能影响不大，但能提高结构高频阶段的隔声性能。

2.4 多孔吸声材料厚度对模型隔声量的影响

针对BB型、BU型和UU型3种模型，改变多孔吸声材料厚度，分析模型隔声性能的变化。

本节的模型参数和隔声计算条件与 2.2节相同，仅仅改变多孔吸声材料的厚度。选取的多孔吸声材料厚度为15、25、35和45 mm，可计算出BB型、BU型和UU型3种模型的隔声量变化曲线，结果分别如图9～11所示。

通过图9～11的计算结果，可分析得出相关结论：在低频阶段，随着多孔吸声材料厚度的增大，结构的隔声量逐渐增大；随着分析频率的增大，多孔吸声材料厚度越大的结构越先出现结构的共振隔声低谷；当频率大于结构共振频率点时，结构的隔声量又会提升，且多孔吸声材料厚度较大的结构依旧表现出较优的隔声性能。总体上讲，拥有较厚多空吸声材料的结构具有更优越的隔声性能。

图9 多孔吸声材料厚度变化下BB型模型的隔声量变化图Fig.9 STL curves of BB model with different poroelastic material thickness

图10 多孔吸声材料厚度变化下BU型模型的隔声量变化图Fig.10 STL curves of BU model with different poroelastic material thickness

图11 多孔吸声材料厚度变化下UU型模型的隔声量变化图Fig.11 STL curves of UU model with different poroelastic material thickness

2.5 空腔厚度对模型隔声量的影响

本节针对UU型模型，分析空腔厚度对结构隔声性能的影响。UU型模型的基本参数和隔声计算条件与2.2节相同，仅改变UU型模型中前、后两个空腔的厚度。前、后两个空腔厚度取为2、6、12和20 mm。当一个空腔厚度发生变化时，另一个空腔厚度保持不变(7 mm)，结果如图12、13所示。

在图12和图13中，4条隔声量曲线的变化趋势基本一致。相对于低频阶段，空腔厚度对结构隔声性能的影响在高频阶段表现得比较明显。总之空腔厚度越厚，其结构的隔声性能越好。

图12 前空腔厚度变化时UU型模型的隔声量变化图Fig.12 STL curves of UU model with different thickness of front air gap

图13 后空腔厚度变化时UU型模型的隔声量变化图Fig.13 STL curves of UU model with different thickness of back air gap

3 结 论

本文结合Biot理论和Bolton的多层板理论，求解了水下多孔吸声材料夹层板的隔声量，分析了3种理论模型的隔声性能以及多孔材料厚度和空腔厚度对结构隔声量的影响。水下3种理论模型的隔声性能，UU型的最好，BB型最差。夹层板中空气腔的存在较好地提高了结构的隔声性能。多孔吸声材料能有效地避免空腔驻波共振的出现，且能提高结构的高频隔声性能。随着多孔吸声材料厚度和空腔厚度的增加，结构的隔声性能也逐步提高。