几何展开与折叠算法及应用综述

孙晓鹏 刘诗涵 王振燕 李娇娇

1(辽宁师范大学计算机与信息技术学院计算机系统研究所 辽宁大连 116029)

2(智能通信软件与多媒体北京市重点实验室(北京邮电大学) 北京 100876)(cadcg2008@hotmail.com)

Fig. 1 Unfolding and folding classification

展开与折叠是计算机图形学领域的经典问题之一，是相互对立的2个过程.一般情况下，展开以结构化的状态作为初始状态，以无组织的状态作为终端状态，而折叠与之相反.展开与折叠中的几何处理思想为设计类问题提供解决方法，并广泛应用于工业、建筑、医疗和航天科技等领域.

展开是将3维结构切割成平面集合的过程.通常情况下，若沿3维结构的网格边缘切割，可以将其完全展开.这类问题的关键在于如何找到3维结构的无重叠平面网结构.然而，对于难以完全展开的复杂模型，如非凸多面体等，可以采用映射方式将其近似展开.近似展开问题的关键是如何最小化失真度量，即在变形影响最小的情况下，将3维模型映射到平面域中.本文根据展开程度不同，将展开问题分为完全展开和近似展开2个部分论述.

折叠是2种结构间的连续运动过程.本文根据折叠形式的不同，将折叠分为Origami折叠和Kirigami折叠2类.其中，Origami折叠仅根据平面折痕折叠，可分为刚性折叠(直折痕)和弯曲折叠(曲线折痕)；而Kirigami折叠是先将平面切割，后利用切割产生的弹力或外力驱动折叠.

本文对展开与折叠问题进行系统的研究与阐述，主要贡献有5个方面：1)整理展开与折叠算法的基本概念，并从机器人设计、计算机动画、深度学习和其他4个领域介绍展开与折叠问题的应用情况；2)根据展开程度的不同，从完全展开和近似展开2个方面讨论展开算法的研究进展，分析并讨论其优缺点；3)根据折叠形式不同，从Origami折叠和Kirigami折叠2个方面讨论折叠算法的研究进展，并分析讨论其优势与不足；4)总结展开与折叠算法的评估准则，并对典型的展开与折叠算法进行分析和比较；5)总结并提出展开与折叠方向的4个发展趋势.

1 基本概念及应用情况

通过分类与整理展开和折叠相关文献，本文根据展开程度不同，将展开问题分为完全展开和近似展开；根据折叠形式不同，将折叠问题分为Origami折叠和Kirigami折叠2类，如图1所示.本节分别对它们的基本概念进行整理和总结.此外，从机器人设计、计算机动画、深度学习和其他4个领域介绍展开与折叠的应用情况.

1.1 展 开

本文根据展开程度不同，从完全展开和近似展开2个部分介绍.

完全展开能够将3维结构无重叠、无变形地展开到2维空间，形成多面体网结构.完全展开的切割条件通常限制在多面体网格的边上(非必须条件)，即边展开.此外，基于最短路径的源展开和星展开方法也是常用方法之一.Demaine[1]介绍启发式3维结构展开算法，但仍存在一定问题，例如最陡边缘展开算法虽然能展开多面体，但部分情况未能避免重叠.

由于大多数曲面是不可完全展开的，因此只能通过寻找近似的展开结构求解问题.近似展开方法确保3维结构在无拉伸的条件下被切割和展开到平面中.曲面可展的充要条件是曲面上任意点的高斯曲率为0，这一条件成为许多网格曲面展开方法的基础.例如，保角映射方法通过消除角度失真，确保3维曲面在无拉伸的情况下展开.此外，为减小保角映射过程中的面积失真，部分文献[2-3]采用添加锥奇点的方式将3维结构映射到规则多面体上，如正方体、六面体等，再进行完全展开.

1.2 折 叠

本文根据折叠形式不同，从Origami折叠和Kirigami折叠2个角度介绍.

Origami折叠是沿折痕折叠的形式.根据折痕分类，Origami折叠又分为刚性折叠和弯曲折叠.其中，刚性折叠沿直折痕折叠，其形变只发生在折痕处，其他位置不发生拉伸或扭曲；而弯曲折叠沿曲线折痕折叠，曲线折痕连接的2个面需要弯曲以适应折叠运动，因此弯曲折叠不能简化为计算顶点坐标的问题，其弯曲刚度也是重要参数.

Kirigami折叠是将切割与折叠结合的形式，可应用在建筑设计[4]和工业设计[5]中.应用Kirigami折叠技术制造的晶格结构[6-7]、可拉伸结构[8]、纳米结构[9-10]以及拉胀结构[11]得到广泛关注.其中，由Kirigami制成的拉胀结构大多是由铰链连接的旋转单元构成，旋转单元为平面切割而成的刚性几何结构(通常为正方形或等边三角形).当拉伸或收缩时，旋转单元围绕铰链旋转以使整体结构变形，而旋转单元本身不发生形变.在变形过程中，拉胀结构表现出的负泊松比变化，称为结构的拉胀行为[12].

1.3 应用情况

本文从机器人设计领域、计算机动画领域、机器学习领域以及其他领域4个角度出发，介绍展开和折叠的应用情况.

1.3.1 机器人设计领域

在机器人设计领域中，折叠机器人具有柔软性，其形态、功能或驱动方式通过折叠产生，能适应各种环境，满足应用中对于灵活性和健壮性需求.

2017年，Miyashita等人[13]提出通过自折叠“外骨骼”变形方法扩展和改变机器人功能.“外骨骼”为长方形薄片，在运动过程中利用预拉伸热收缩聚合物薄膜的拉伸应力实现自折叠.相较于固定架构的机器人，自折叠“外骨骼”机器人操作更灵活，可应用在空间制造、无切口医疗、深海建设和现场救援等场景中.

2017年，Li等人[14]结合折纸思想，提出由流体驱动的人工肌肉结构(fluid-driven origami-inspired artificial muscles, FOAMs).FOAMs由柔性皮肤膜、可压缩实体骨架和流体介质构成.在内部流体与外部间的压强差作用下，皮肤膜驱动收缩：当缩小内部流体体积，即在负压下，压强差Δp会使皮肤膜弯曲，推动FOAMs收缩变形.表1对折叠驱动的人工肌肉结构(pleated pneumatic artificial muscles,PAMs)、真空驱动的人工肌肉结构(vacuum-actuated muscle-inspired pneumatic structures，VAMPs)、FOAMs进行对比总结.与正压差驱动对比，负压差的驱动方式更安全.

Table 1 Comparison of Fluid-Driven Artificial Muscles

2018年，Rus等人[17]将折叠技术与智能材料结合，设计折纸机器人，并采用3D,4D打印等方法制造.与传统机器人相比，折纸机器人能够通过折叠进行变形或连续驱动，在特定的环境下能够实现灵活自主的移动与操作.

2019年，Li等人[18]利用折纸技术设计软抓取器，提出具有抓取功能的软机器人制造及真空驱动方法.如图2所示，软抓取器为轻质量空心半球状水弹结构，通过引入FOAMs方法[14]驱动，实现抓取操作.与刚性抓取器相比，软抓取器具有强大的抓取力(在-60 kPa下保持高达120N的载荷，超过自重的120倍)和健壮性(允许在40%的轴向偏移处抓取).

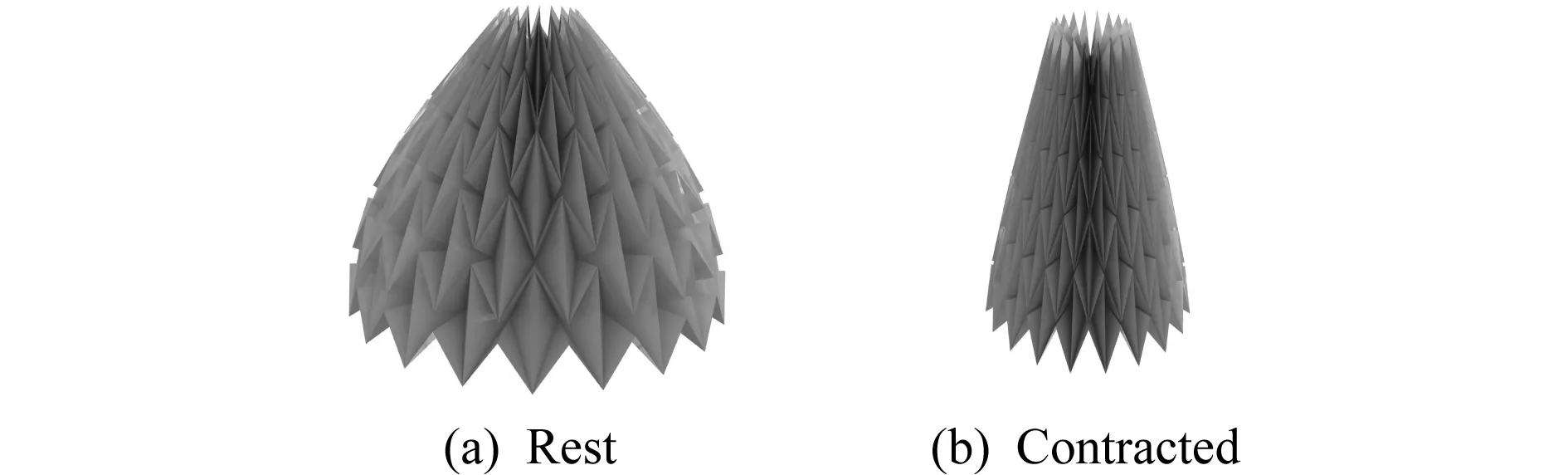
Fig. 2 Soft grabber of waterbomb structure[18]

1.3.2 计算机动画领域

模拟是计算机动画领域的重要问题之一.只有捕捉悬垂、折叠、起皱、拉伸等细微元素，才能提高电脑模拟时的真实感.2003年，Bridson等人[19]提出将数字替身所穿服装与现实中服装匹配方法，用于保留并处理在布料模拟中的褶皱形态.

2010年，Rohmer等人[20]将粗布动画与后处理步骤结合，生成精细的动态皱纹.该方法允许用户在不同织物上模拟.除用户控制的参数外，其余为全自动过程.但是，尽管该方法保留褶皱的形状，却不能保证创建的曲面是可展的.

2013年，Narain等人[21]提出模拟纸、金属凹痕、布等薄板材料的塑性变形方法，通过使用自适应网格框架，将网格的边与褶皱或折痕动态对齐.该框架能够对尖锐特征进行有效的建模，并避免由于平面刚性行为而无法弯曲的问题.

2015年，Patkar等人[22]提出尖锐折痕弯曲单元，既可在布料或纸张中创建褶皱，还可以用于在体积对象中创建类似的屈曲.其关键思想是利用弯曲弹簧模拟分割，使用虚拟节点算法切割对象后，使相邻面片只围绕切割旋转或弯曲，并利用前稳定和后稳定方法添加约束条件.

2018年，Li等人[23]提出FoldSketch算法，通过物理模拟布料，保证输出结果的物理合理性，首次实现基于草图的褶皱设计.然而，该方法并不能生成复杂褶皱，如在特殊材质或需要缝合的布料上模拟.

2018年，Feng等人[24]提出光滑粒子流体(smoothed-particle hydrodynamics, SPH)形变约束方法，以保持流体模拟中的细节.该方法将输入模型分为源对象和目标对象，分别采用体素化方法采样以生成源控制粒子和目标控制粒子；之后进行约束变形.该方法具有快速性和健壮性，适合交互应用.

2019年，Liu等人[25]利用可变形物体的不均匀性计算不同区域特性，增加结果的真实性.此外，通过组合浮力、压力、粘性力和弹性力，设计计算框架，保留更多细节.

1.3.3 深度学习领域

高度复杂和非凸的模型存在具有无碰撞路径的多面体网结构.深度学习方法可通过训练节点自由度(degree of freedom, DOF)、切割长度或展开面积等拓扑特征，快速找到低成本的有效折叠或展开路径.2014年，Zhou等人[26]提出利用连续折叠序列将3维物体转换为立方体或长方体的方法，主要包含体素化、树拟合和交互折叠3个步骤：1)体素化过程主要寻找减少小块体素数量的分割方式；2)树拟合过程使用束搜索和模拟退火算法寻找使能量函数最小化的关节类型和位置；3)交互折叠过程使用物理模拟器来展开输入形状和目标形状，验证折叠过程是否无碰撞.

2016年，Xi等人[27]提出自动折叠方法，即通过学习自展开方法，同时展开和分割给定的3维网格.其关键思想是从失败的展开中学习算法，通过提供语义，减少分割数量，使折叠更加容易.

2018年，Hao等人[28]提出线性可折叠多面体网创建方法，也是具有线性无碰撞折叠路径的展开方法.首先将多面体网映射到低维特征空间X中，评估X中每个点的可折叠性；之后根据拓扑特征构造适应度函数，通过展开器f′生成不重叠展开网N[28]：

(1)

1.3.4 其他领域

可弹出结构设计常应用在立体纸雕或立体书的设计中.对于常用结构，如V-Fold结构，必须满足的性质[30]有：在不撕裂或引入新折痕的前提下，结构可以关闭到平面上，且每次弹出都生成相同形状；贴片在关闭和弹出过程中保持刚性；不相连的贴片在关闭或弹出时不相交.表2总结6种可弹出结构设计的研究和工作内容.

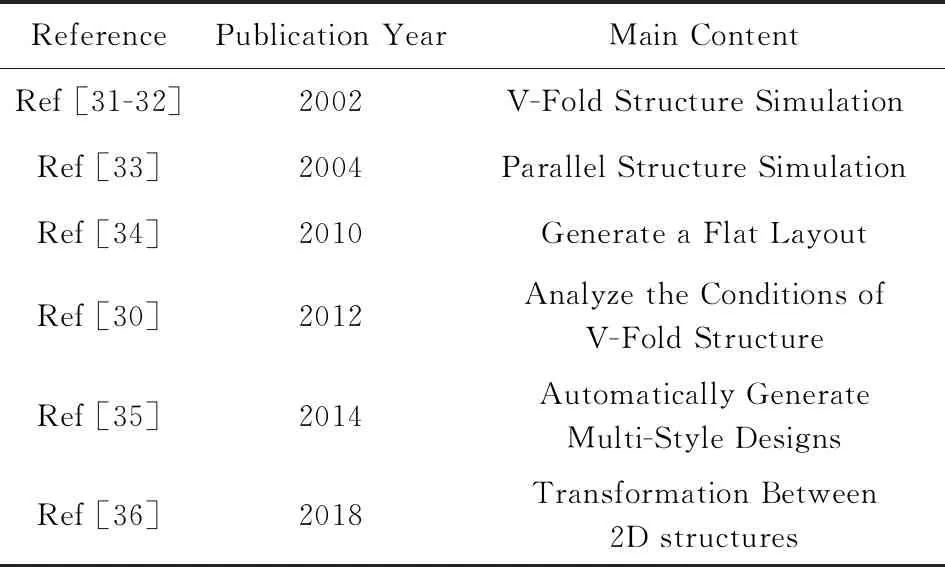
Table 2 The Application of Pop-up Structure

Li等人[37]将折叠问题应用到家具设计中，即通过在分段刚性的部件上插入铰链，折叠收缩家具，节省存放空间.该方法在36个不同类型的家具模型上测试，除专门设计的可伸缩性测试模型外，大多数模型都可折叠收缩，具有较好的健壮性.

计忠平等人[38]和张世学等人[39]利用边折叠技术进行模型简化工作：文献[38]通过半边折叠简化网格并保留网格细节特征，不仅运行速度快，而且存储量小；文献[39]使用变形距离模拟模型的变形程度，并使用基于二次误差度量的累加边折叠代价简化模型，易于输出高效模型.

2 展开算法研究进展

本节根据展开程度分类，从完全展开和近似展开2个方面论述展开算法的研究进展，并对典型算法的主要工作、算法思想及优缺点进行总结.

2.1 完全展开

2008年，Miller等人[40]对凸多面体进行研究：若Pb为d+1维的凸多面体边界，该方法证明Pb到Rd空间中存在单一非重叠展开多面体网.此外，他们还提出凸多面体边界上的最短路径数猜想，用于连续展开凸多面体.2010年，Itoh等人[41]将星展开概念扩展到多边形闭合曲线Qc中：将任意凸多面体P的表面展开成简单不重叠的平面多边形，只需沿着P到Qc中每个顶点的最短路径进行分割.2011年，Demaine等人[42]研究任意凸多面体单一非重叠平面形式展开方法，包含2步：使用源展开方法连续展开凸多面体；细化凸多面体的展开部分，并使用蛇形展开算法生成更为连续的平面展开形式.

2011年，Takahashi等人[43]提出三角形非凸多面体网格展开算法：通过计算曲面曲率，将网格顶点分为双曲线顶点和椭圆顶点，并使用基于遗传的方法搜索自适应采样网格展开.该方法无需将3维网格展开到平面上，便可检索局部自交情况，加快对无重叠单连通展开速度.

2015年，Xi等人[44]将多面体建模为多连杆树结构，并在离散域中采样，解决连续展开多面体问题.多连杆树结构的铰链为展开结构中的共享边，折叠角为铰链处二面角的补角.设多连杆树当前结构C={θ1,θ2,…,θn}，初始结构S={ρ1,ρ2,…,ρn}和目标结构G={0,0,…,0}，θ和ρ分别为当前结构和初始结构的折叠角.通过线性插值初始空路径图R，判断生成的中间结构C是否能直接连接初始结构S和目标结构G；若可连接，则找到有效展开路径，反之使用离散采样器采样折叠角的完全展开状态、目标状态以及完全折叠状态{0,ρi,π}，并通过连接器添加到R中，若R中的路径有效，则找到展开路径，否则再次采样，直到找到有效路径.文献[44]比较连续采样器与离散采样器生成有效结构的能力：连续采样器在7DOF空间中有效率为38%左右，而离散采样器的有效率超过70%；在43DOF的空间中，连续采样器的有效率为0.06%，而离散采样器为58%，说明离散采样器具有高效性.但是，对于大型非凸多面体，若S和G不能线性连接，则很难生成有效的展开路径.

在完全展开算法中，文献[40-42]主要计算凸多面体的单一非重叠展开，其中，文献[40,42]使用源展开方法，文献[41]使用改进的星展开方法.文献[43-44]主要针对非凸多面体展开，但文献[43]通过遗传方法优化展开的贴片数量，即展开图案不单一；而文献[44]通过离散采样找到有效的展开路径，但无法计算非线性连接的非凸多面体.

2.2 近似展开

2003年，陈动人等人[45]利用伪直母线对拓扑结构复杂的曲面结构进行自适应分片展开，大幅度提高展开质量.2006年，Kharevych等人[46]提出基于圆模式的离散保角映射展开算法，通过求解每个三角面片外接圆的半径以及各个外接圆之间的交角，确定平面展开布局.该算法可以控制映射的边界形状，具有健壮性.2007年，Zayer等人[47]使用角度误差估计方法，首次提出保角映射的线性算法.2008年，Mullen等人[48]通过求解包含稀疏对称矩阵的广义特征值问题的最大特征值，最小化离散加权保角映射能量，计算展开结果.2012年，文献[3]提出全局保角映射展开算法，通过确定圆锥位置和角度，展平曲面.

2018年，Soliman等人[50]提出添加锥奇点(锥数量、大小和位置)的最小失真(minimal area distortion, MAD)展开算法，包括最小总面积失真展开、控制锥位置并惩罚失真区域展开、计算最优边界形状展开和控制锥角范围展开4种.MAD算法的根本目标是在输入模型M(若有边界记为Mb)上找到1组锥点pm∈M和相应的锥角θm∈R，使展开后的面积失真最小，即[50]：

(2)

u=0, onMb,

其中,能量EM测量面积失真，u为保角缩放因子，Δ是拉普拉斯算子，K为初始高斯曲率，δp表示p的Dirac delta度量.MAD算法只需求解50～100个线性系统，且不依赖模型分辨率，无论使用均匀还是可变密度的网格，都能用少量的锥计算，具有良好的健壮性.但是，文献[50]并未考虑量化角度的最优锥构型问题(例如，锥角设置为π2的整数倍).

2018年，Sharp等人[51]提出全局变分展开算法.不同于显式参数化曲面算法，该算法通过定义切割曲线γ的演化方程，直接优化切割和展开过程中的变形[51]：

(3)

其中，n是曲线γ的单位法线，u是保角缩放因子.该算法对于初始切割线的依赖性小，具有较好的健壮性.虽然在平滑条件中不会出现多个分割区域合并或单个区域一分为二的情况，但会产生较窄的区域，在离散条件下可能会出现夹点.

对于近似展开算法，文献[45]通过伪直母线展开曲面，却无法控制展开的边界形状；文献[3,46-47,49-51]通过保角映射寻找近似展开结构，确保展开过程中的面积失真最小.其中，文献[46-47,49]可以控制展开边界形状，但文献[46-47]无法控制边界长度，而文献[49]既可控制边界长度，也可控制边界角度.此外，文献[49-50]使用参数化方法展开曲面，而文献[51]仅通过优化切割曲线方程寻找最优切割路径.

3 折叠算法研究进展

本节根据折叠形式的不同，从Kirigami折叠和Origami折叠2个方面介绍折叠算法研究进展，总结它们的主要工作、算法思想并讨论其优势与不足.

3.1 Origami折叠

本节对Origami折叠的相关文献进行整理，按照折痕形式将Origami折叠分为刚性折叠和弯曲折叠.同时总结其中典型文献的主要算法和优缺点.

3.1.1 刚性折叠

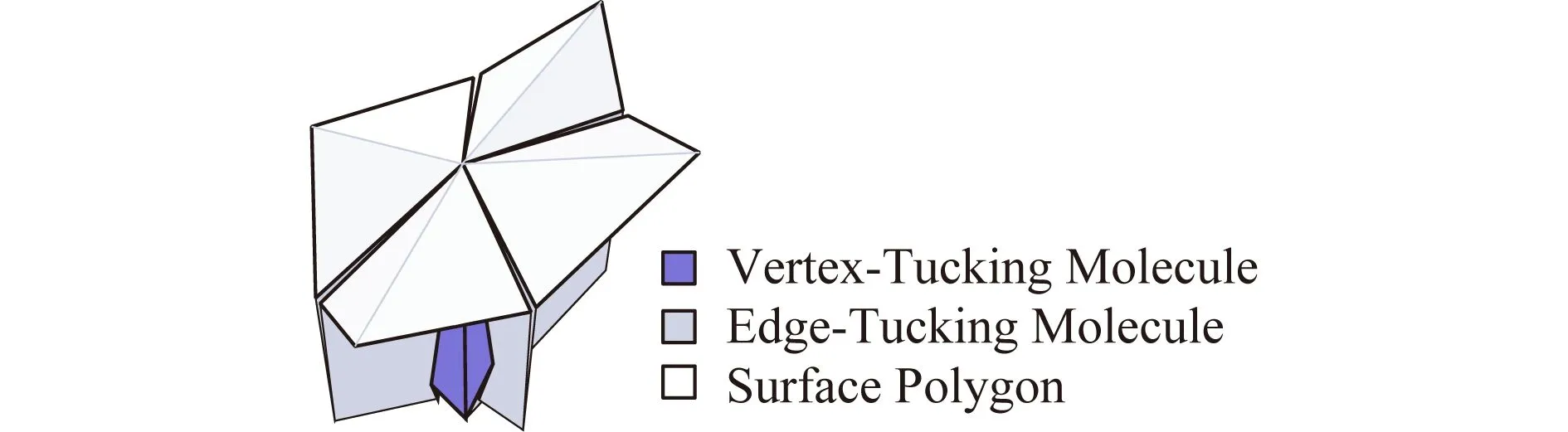
Fig. 3 The folding molecules are hidden behind the surface[52]

2010年，Tachi[52]提出2维纸结构在无切割、无拉伸条件下折叠成3维目标结构的逆设计算法，其关键在于将3维折纸问题转化为在平面上布置多边形的问题，之后通过插入折合分子连接相邻的多边形(折合分子隐藏在可见表面后面)，如图3所示.此外，通过构造有效折痕图案所需的等式和不等式条件，提出基于2步映射和边缘分割的算法.但是，该算法并不适用于任意模型.

2015年，Chen等人[53]提出厚板结构刚性折叠方法，根据零厚度刚性折叠结构设计的2维折痕图案，实现零厚度与非零厚度材料间的等效运动.零厚度刚性折叠运动可看作是球面连杆结构运动，折痕看作为旋转关节J，以折痕为界的面看作为连杆.非零厚度刚性折叠运动通过实现与零厚度的球面连杆结果相同的运动条件(折痕排列及折叠角度)，完成折叠过程.4折痕图案存在1个空间4J连杆；而5折痕和6折痕图案包含2DOF或3DOF，但其对应的非零厚度材料是空间过约束Bricard连杆结构，只有1 DOF.因此若要实现5折痕和6折痕零厚度折叠与非零厚度折叠之间运动的等效，需要通过对称或其他方式降低前者的自由度.

2016年，Chen等人[54]分析6折痕水弹折叠问题及其非零厚度折叠运动.如图4所示，6折痕水弹图案包含2类顶点：顶点D(4条谷折痕、2条山折痕)、顶点W(2条谷折痕、4条山折痕).文献[54]证明，在通常情况下，具有顶点D和顶点W的折叠图案存在2种不同的折叠方式，但是在折叠过程中可能会出现2级运动或阻塞情况.

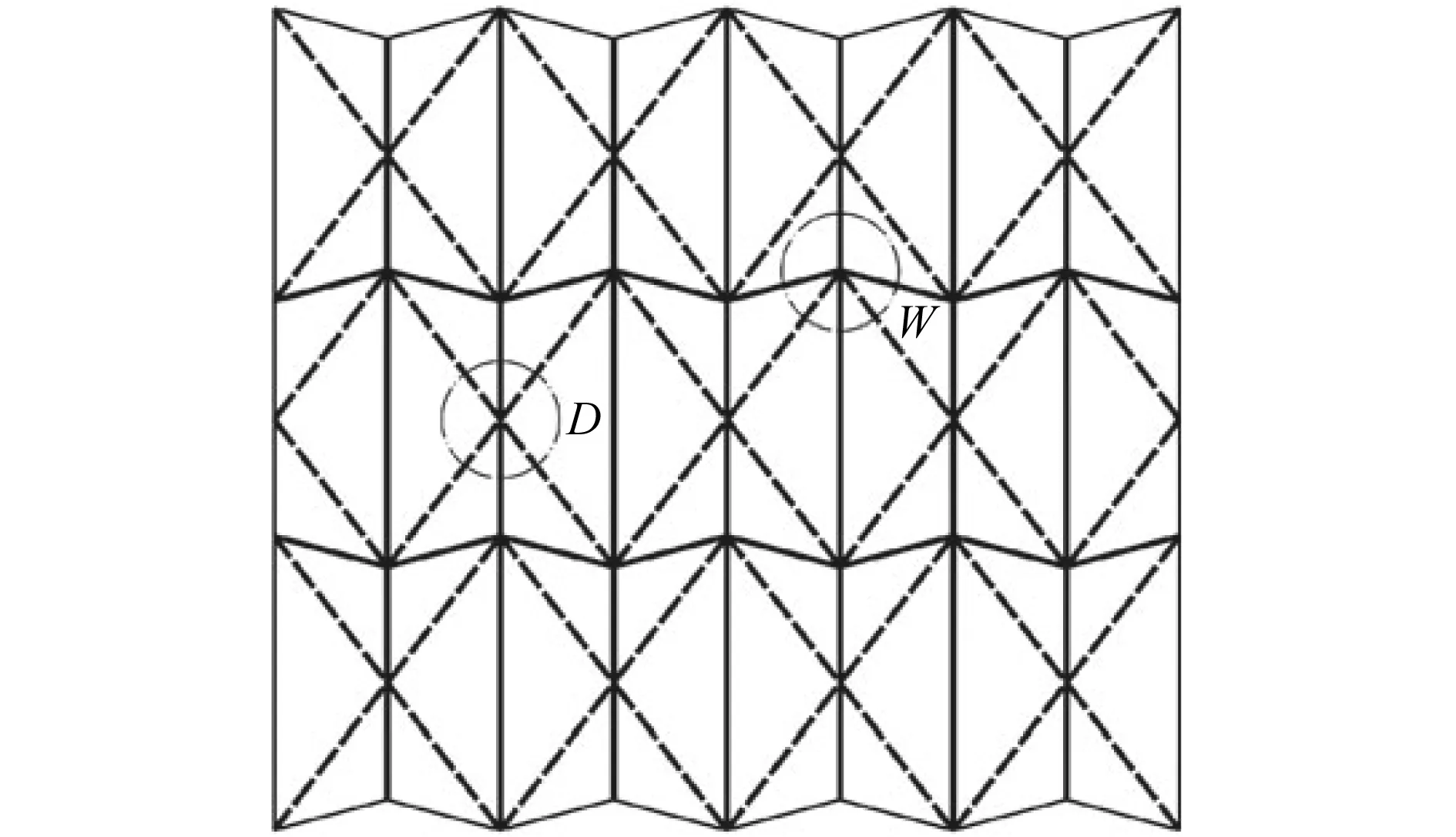
Fig. 4 Six fold waterbomb pattern vertex D and vertex W [54]

与零厚度折叠相比，非零厚度折叠的优点在于：1)非零厚度折叠结构是仅具有1DOF的过约束Bricard连杆结构，不需要其他约束保持运动的对称性；2)零厚度折叠运动具有奇异性，而非零厚度折叠运动只有在特定厚度下才会出现2条路径，有利于工程应用.

对于刚性折叠方法，文献[52]通过引入折合分子，无分割和撕裂地折叠零厚度平面结构；文献[53-54]主要研究零厚度结构与非零厚度结构间的运动关系：文献[54]在文献[53]的基础上，总结零厚度结构与非零厚度结构的折叠路径及折叠条件.

3.1.2 弯曲折叠

2012年，Solomon等人[55]将离散可展曲面看作是在无撕扯或粘合条件下折叠的纸结构，提出离散可展曲面交互建模方法.为确保每个模型对应唯一的离散可展曲面，需要满足3种约束条件：几何约束、兼容性约束和附加约束.

2016年，Tang等人[56]提出可展曲面建模和折痕设计算法.该算法通过样条曲线近似用点云表示的参考模型，并通过分段可展的方法生成水密复合的可展曲面.首先，通过将平面局部拟合到点云上，计算参考形状的剩余点qj中的法向量mj；之后线性插值样条曲线a,b，得到条带φ的曲面s；最后使用引导投影算法将qj投影到可展曲面s上.该算法适用于任意复杂的可展曲面：对于参考形状中的区域ψ1,ψ2,…分别用条带φ1,φ2,…近似，之后合并条带φ1,φ2,…并在边界处添加近似约束，形成水密曲面.然而，该算法的区域是用户定义的，因此并未解决最佳布局问题，也未考虑到连续近似和重叠问题.

2017年，Kilian等人[57]提出弦驱动的折叠算法，解决在等距变形空间中局部表示折叠路径以驱动折叠的问题，简化弯曲曲面的折叠运动过程.该算法先计算2维折痕图案的折叠运动，后计算在拉力驱动下产生相同折叠序列的弦网络.但是，该算法只适用于在拉力作用下折叠而成的曲面结构，对于其他力荷载下成形的曲面结构无效.

2017年，Guseinov等人[58]提出利用弹力驱动曲率变化的壳结构设计算法(CurveUps),将含有预弹性力的薄膜覆盖在硬质体结构上，当释放弹力时，体结构相互碰撞挤压，迫使整体趋近于3维目标结构.算法通过2步优化，生成2维的硬质体结构布局：1)全局优化，定义软约束表示结构的期望特性，定义硬约束用于捕获制造和驱动限制；2)局部优化，利用弹力对模型参数的局部依赖性解决体结构间的无效碰撞.由于相邻体结构间的局部可压缩性和二面角约束影响，该算法并不适用于任意模型.

对于弯曲折叠，文献[56-58]皆用于构建3维结构，但文献[56]仅适用于可展曲面，文献[57]仅适用于拉力成型的3维结构，而文献[58]使用弹力驱动折叠，不能保证从平面初始状态到最终状态的自驱动性，往往需要手动操作驱动变形.

3.2 Kirigami折叠

2014年，Cho等人[59]提出分层分割旋转单元的方法.相较于原始的旋转单元结构，该方法不需要改变材料的物理性质，便可增强目标结构的特性，扩展材料的设计空间，提高伸展性能.

2015年，文献[11]利用软膜Kagome结构(如图5所示)的屈曲不稳定性，通过控制铰链宽度，提出具有预扭角度的变形方法：指定单元间的预扭角度，控制整体结构的变形路径、变形模式、刚度和负泊松比.该方法提供确定性的变形方式，并防止屈曲的不稳定性.

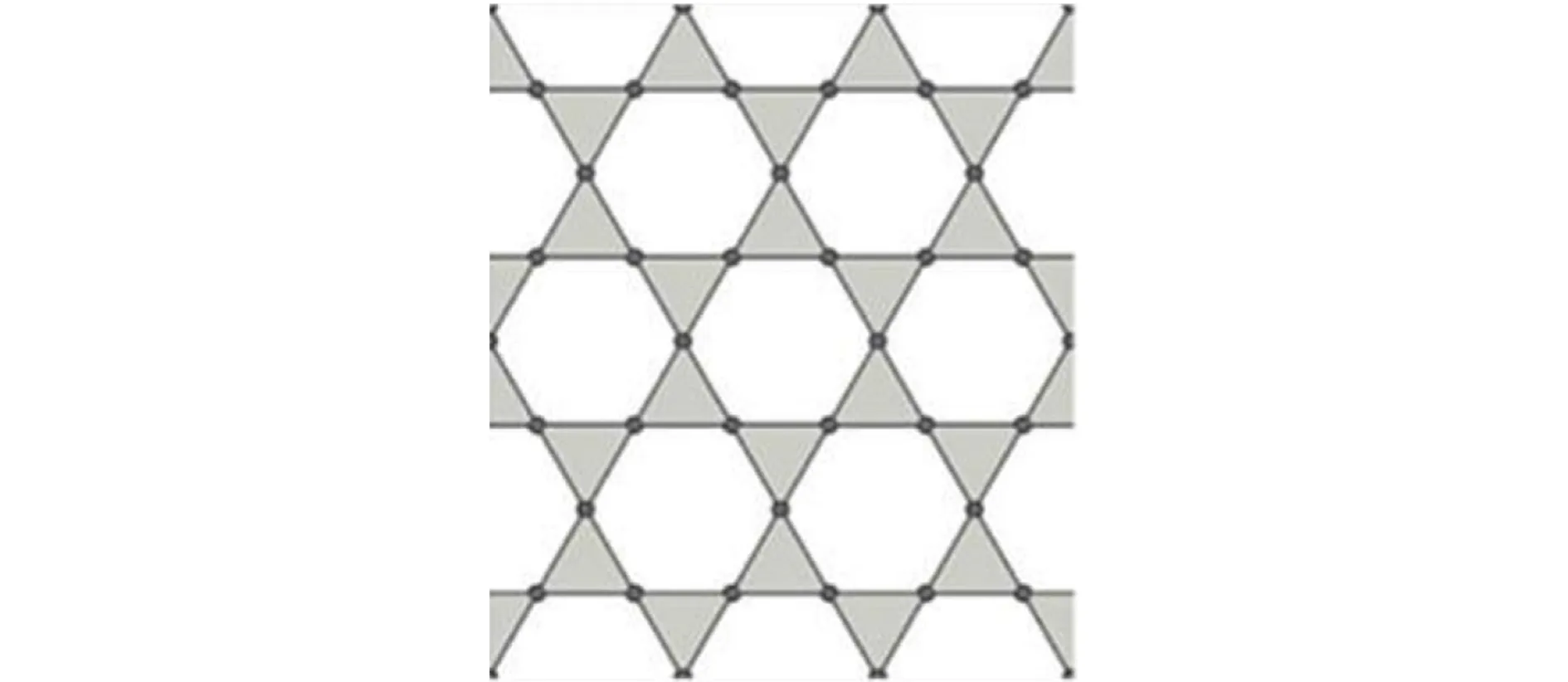
Fig. 5 Kagome[11]

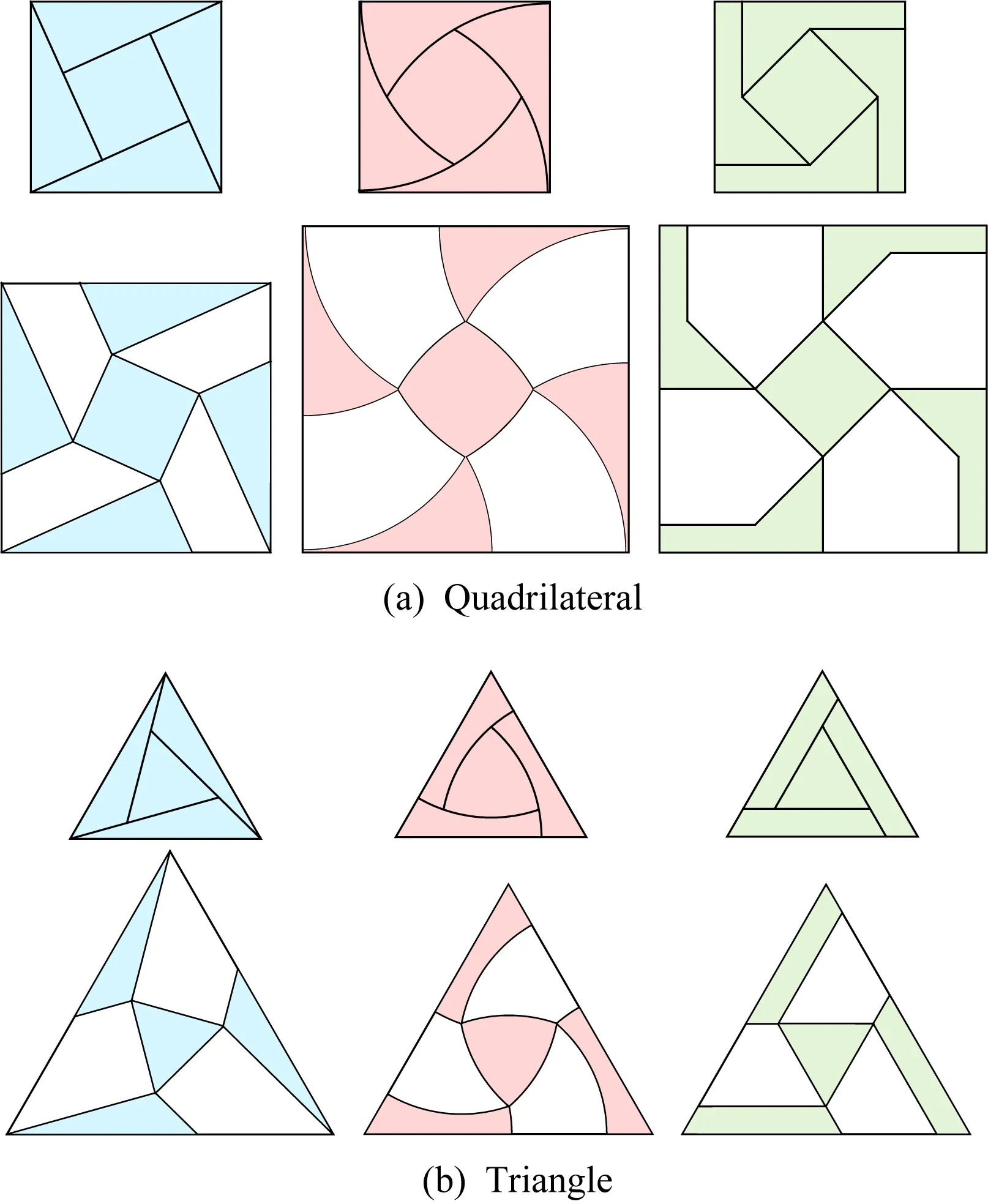
Fig. 6 Cutting and expansion structures of quadrilateral and triangular units[60]

2016年，Rafsanjani等人[60]提出双稳态拉胀结构设计方法，通过切割创建刚性旋转单元，在力的作用下可实现2种平面结构的转换，并保证变形结构的负泊松比和双稳态性.刚性单元是在正方形或等边三角形的基础上切割而成，如图6所示：

2019年，Choi等人[63]提出使用力学模型模拟2维与3维的Kirigami结构变形过程，可以控制变形结构的稳定性和变形的路径.该力学模型将旋转单元的边模拟为拉伸弹簧，相连的铰链模拟为扭转弹簧，通过最小化变形能量E，得到连续的变形路径.变形能量E的公式为[63]：

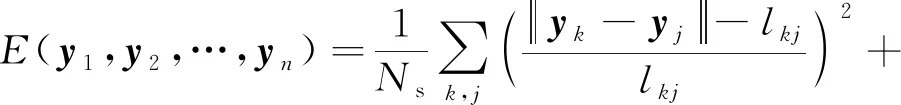
(4)

其中，yk表示旋转单元顶点k位置，θk表示分割线间的角度，lkj为拉伸弹簧kj静止状态下的长度，Ns为拉伸弹簧的数量，Nc为扭转弹簧的数量，λr是扭转弹簧常数与拉伸弹簧常数之比.λr越大，铰链越宽，其闭合倾向也越大.因此当λr→0时，其变形结构趋近于双稳态.

对于Kirigami折叠，文献[59-60]通过对刚性单元进行二次分割，增强结构特性，如文献[59]提高结构的拉伸能力，文献[60]提高结构的稳定性.文献[61-62]实现2维与3维结构的转换，提出逆设计算法.但文献[61]无法保证刚性单元完全展开，而文献[62]在此基础上使用膨胀力和重力荷载解决局限性.

4 分析与讨论

本节总结展开及折叠算法性能的评价指标，并分析典型展开及折叠算法.

4.1 算法评价指标

通过对已有文献的整理研究，4.1.1节总结展开算法的评价指标，4.1.2节总结折叠算法的评价指标.

4.1.1 展开算法

展开算法的评价指标分为2类：完全展开指标和近似展开指标.

1) 完全展开

完全展开的评价指标包括展开数量(Np)、展开时间(Tu)、拓扑特征(NDOF)、面积比(Aarea).其中，拓扑特征NDOF可根据多面体网的自由度评定，定义为[28]:

(5)

其中，Nleaf表示展开的多面体网1级节点数量，N表示多面体网的总节点数量.

面积比Aarea提供多面体网的分支间隙信息，是多面体网的包围盒面积AH与表面积AD之比[28]：

(6)

如果Aarea接近1，表明多面体网是紧密相连的.

2) 近似展开

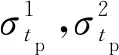
(7)

(8)

或通过计算模型M的Dirichlet能量衡量，即测量映射过程中的全局缩放因子u的变化，定义为[50]：

ED(u)

(9)

当ED越趋近于0，面积失真越小；对于无法用Dirichlet能量测量的情况，可使用L2范数测量[50]：

EL(u)

(10)

此外，还可通过对比锥数量ncone和总锥角w评定，总锥角w可定义为[50]：

(11)

4.1.2 折叠算法

折叠算法的评价指标分为2类：Origami折叠和Kirigami折叠指标.

1) Origami折叠

Origami折叠的评价指标包括折叠时间(Tf)、曲面平整度(δs)、可展性(K)、折叠的效率(ηori)、近似误差(H).对于四边形可展条带拟合的可展曲面，可根据曲面平整度δs评估曲面质量，定义如下[56]：

(12)

其中，ls为四边形条带的对角线距离，as为四边形条带的2个短边长度的平均值.

曲面的可展性通过计算高斯曲率K判断，定义如下[56]：

(13)

其中，θj是顶点i的一环邻域角度，j为顶点i的一环邻域面片数，Amixed是i的一环邻域的混合面积.

折叠效率ηori为模型的表面积Apr与折叠所需的平面材料的表面积Aori之比[52]：

(14)

近似误差H可根据生成模型M1与目标模型M2间的Hausdorff距离计算，公式为[65]：

H=max{h(M1,M2),h(M2,M1)},

(15)

其中，h(M1,M2)，h(M2,M1)分别为从M1至M2和从M2至M1的单向Hausdorff距离.

2) Kirigami折叠

Kirigami折叠的评价指标包括稳态性(η)、最大相对顶点偏差(ρmax)和孔隙度(Sh).对于由Kirigami技术制造的旋转单元拉胀结构，稳态性η定义为变形稳定状态下的局部最小应变能Emin与其最大应变能Emax之比[60]：

(16)

当η<1时表明结构具有双稳态性，η=1表明具有亚稳态性，η>1表明具有单稳态性.

最大相对顶点偏差ρmax计算为[62]：

(17)

其中，Dmax为生成结构中顶点与目标结构中对应顶点间的最大距离，L为目标结构包围盒对角线的长度.

孔隙度Sh表明Kirigami变形结构的孔隙大小，计算公式为[63]：

(18)

其中，Sd表示变形结构的孔隙面积，S0表示结构覆盖区域的面积.

4.2 算法分析与比较

根据4.1节的展开与折叠算法评价指标，对典型的展开与折叠算法进行分析和比较.

4.2.1 展开算法

关于展开算法研究工作的分析与比较结果如表3所示，主要比较因素包括分类、相关文献、发表年份、评价指标及特点.

Table 3 Comparison of Unfolding Algorithms

在完全展开算法中，实验结果表明：文献[43]的计算时间随着网格面数的增加而增加，并受曲率的影响，其最长展开时间为785.5 s(950个面的fish模型).文献[28]在超过100个面的模型上训练十分耗时：当bunny模型的面数从48增加到128时，训练时间从39 min增加到427 min.

在近似展开算法中，实验结果表明：在文献[2-3,50] 的3种添加锥奇点的展开算法中，如表4所示：当锥数量相同时，文献[50]的失真面积最小；在面积失真相近时，文献[50]放置的锥数量和总锥角更少；当总锥角相近时，文献[50]放置的锥数量和失真面积更小.此外，对于含有100 000～150 000个三角形的模型，文献[50]最多需要20～25 s，优于其他2种算法.在文献[45,69]的2种算法中，文献[45]可以控制展开面片数量，相比于后者的简单带状分割方法，更好地抓住曲面的几何特征，且避免引入不必要的分割.在文献[47,49,67]的3种可控边界的算法中，文献[49]不仅可以同时控制边界的角度和长度，还表现出最小的最大失真面积.最后，在文献[64,68]的2种算法中，文献[68]具有较好的保面性质，但是其可计算的网格有限.

Table 4 Comparison of Three Cone Singularities Unfolding Algorithms[50]

4.2.2 折叠算法

典型折叠算法的分析与比较结果如表5所示，主要比较因素包括分类、相关文献、发表年份、评价指标以及特点.

对于Origami折叠，实验结果表明：文献[52]的折叠效率皆在0.1～0.5之间.其中，直径约为500 mm、厚度约为116 gm2的凸形纸折叠而成的bunny模型，折叠效率为0.172.文献[56]中，不同模型每次的迭代时间为0.04～0.8 s，其实验结果较为平滑.文献[58]的算法可在简单模型和局部高曲率的复杂模型上计算，在Lilium模型上的平均误差小于1 mm，而在20 cm的Spot模型上，其平均误差小于4.3 mm，最大误差为12.8 mm，但是其全局优化时间为1 362 s，局部优化时间为6 205 s，耗时较长.

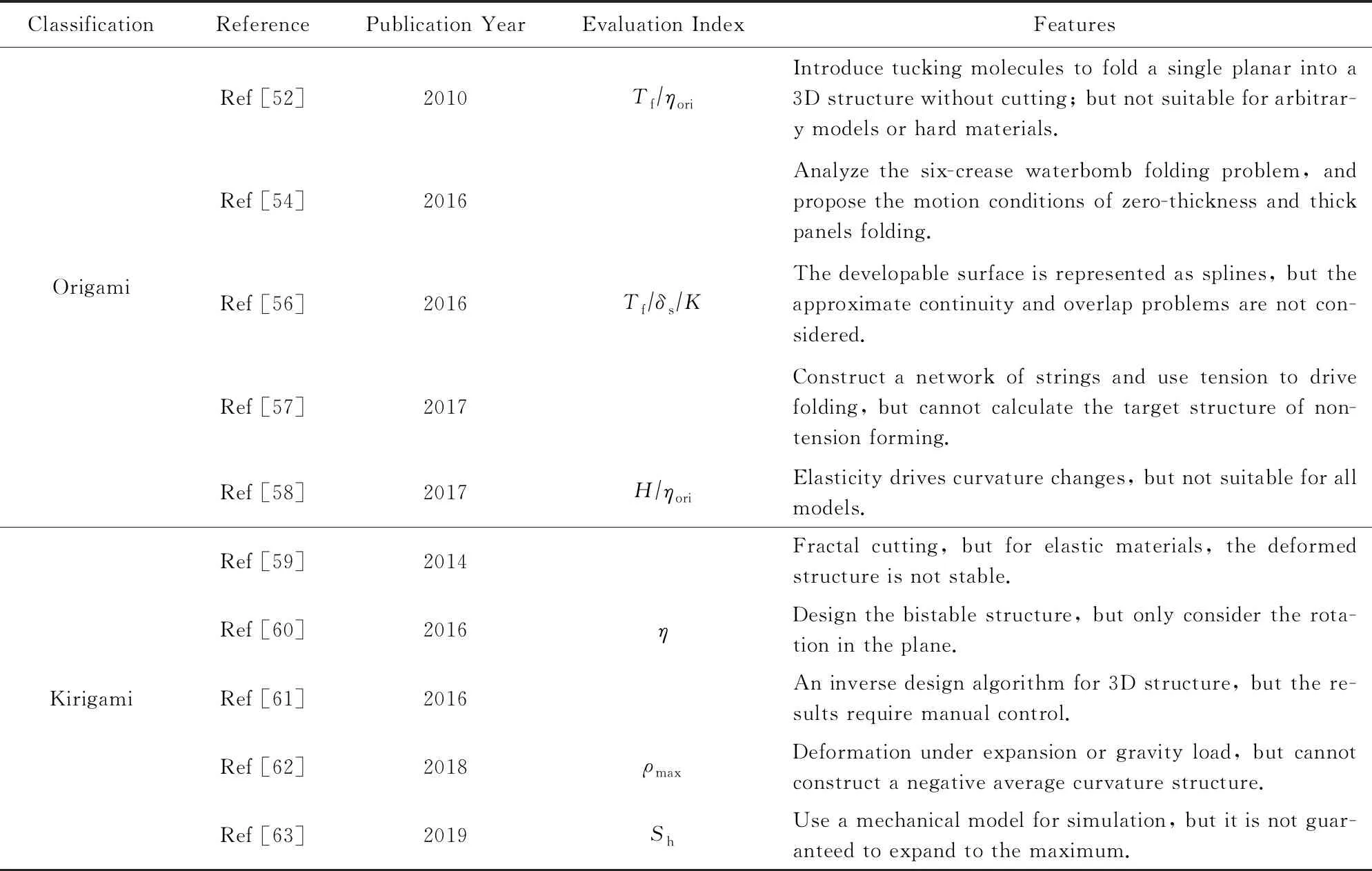
Table 5 Comparison of Folding Algorithms

对于Kirigami折叠，实验结果表明：文献[60]虽然改进传统拉胀结构[59]单稳态性的特点，生成双稳态结构，但其研究仅局限于平面域.文献[61-62]虽然将结构扩展到3维空间，但无法保持双稳态性：文献[61]需要手动控制受力情况，且其3维结构并非完全扩展；文献[62]可在膨胀力或重力荷载下自动生成3维结构，并保证结构完全扩展，其最差的模型相对偏差为0.001 8，误差较小.

5 总结与展望

本文对近年来的几何展开与折叠算法进行综述、分析与比较：在展开方面，根据展开程度，从完全展开和近似展开2方面分别总结并论述其相关研究工作进展；在折叠方面，根据折叠形式不同，分为Origami折叠(包括刚性折叠、弯曲折叠)和Kirigami折叠2类.之后，本文分别给出展开与折叠的评价指标，比较其中的典型算法.此外，本文从机器人领域、计算机动画领域、深度学习领域及其他领域4个方面介绍展开与折叠的相关应用.

目前，已有大量学者对展开与折叠问题进行研究，并提出许多改进算法，但仍存在许多不足，还需进一步研究.本文总结展开与折叠问题的4方面发展趋势：

趋势1. 提高算法的精度和健壮性.

在展开算法中，切割线位置的选取对展开结果有直接影响.对于完全展开算法，需要考虑如何快速精确地寻找最优切割位置；对于近似展开算法，需要考虑如何避免角度或面积失真，计算更近似的平面图案.尤其，对于添加锥奇点的近似展开算法[2,50,67]，除了考虑尽可能减少锥数量和锥角外，可以尝试优化圆锥的几何结构，通过寻找最优的锥结构，减少展开结果的失真，提高精度.

在折叠算法中，Origami折叠需要考虑折叠效率问题，即如何优化约束的折叠过程，在保证折叠连续性的同时避免生成模型的重叠率；而在Kirigami折叠的逆设计算法中，需要考虑如何减少变形结构的误差.

此外，大多数的展开与折叠算法只适用于特定类型的模型中，例如2019年，Hao等人[70]提出的3维凸结构薄板折叠方法.此外，除了计算大型或复杂的非凸多面体的有效展开或折叠路径外，还需要考虑展开结构与折叠结构的互逆过程，确保展开结构可折叠回原模型.

趋势2. 体折叠问题.

大部分折叠算法都是在零厚度材料的基础上研究，而未考虑厚度对于制造应用的影响.文献[26]提出的体折叠算法为相关方向提供基础.此外，在虚拟环境中模拟褶皱是耗时的设计过程，目前的研究大多基于布料或纸张等零厚度材料，文献[22]提出的虚拟节点算法虽然可以在实体对象上模拟褶皱(如皮肤)，但效果并不真实.本文认为，可以将折叠算法应用在实体对象上，并提高结果的真实性.

趋势3. 自驱动过程.

展开与折叠问题适用于众多领域，如何进行自驱动展开和折叠过程一直是重要的研究问题.文献[58]提出使用弹力驱动折叠，但并不能保证整个折叠过程都处于自驱动状态中，对于部分模型，仍需用户参与调节.文献[62]提出使用重力或膨胀力驱动折叠，但其算法只适用于非正平均曲率的双曲面模型.本文认为，在设计展开和折叠算法时，可尝试与已有的智能驱动方式结合，如形状记忆合金[71]、电活性聚合物[72]和流体驱动[73]等，提高计算过程的自驱动能力.

趋势4. Kirigami折叠技术的智能应用.

在折叠问题中，Origami折叠技术一直是科研学者的重点研究对象，而Kirigami折叠技术却未受到同等的关注度，与Origami折叠技术相比，Kirigami折叠技术更适合用于设计高度可伸缩[74-75]和可变形[76]结构.但是，Kirigami折叠技术的设计理论和应用并未完全结合，且并未过多开发相应的设计算法.本文认为Kirigami折叠灵活的伸缩性更适合于机器人领域的应用.例如2018年，Rafsanjani等人[77]利用Kirigami原理，显著提高软体机器人的爬行能力.

此外，由于Kirigami折叠结构能灵活地实现3维与2维结构的转换，且其变形结构具有大量孔隙，同样适用于应用在医疗领域，如智能医用支架设计、智能绷带或皮肤移植等[78]，即减少固体部分的实际表面积的同时，减少因接触异物而引起的炎症，避免治疗的副作用.综上，虽然Kirigami折叠技术未得到完全开发，却具有广泛的研究意义，有待进一步探索.