R 型弯管流动的数值模拟分析

马 影, 孙乐萌

(上海工程技术大学 航空运输学院, 上海201620)

0 引 言

弯管流道广泛存在于工业设备中,例如液压系统、阀门等,流体经过这些弯管时会发生流动分离,引起漩涡,从而引起压降和能量损失,在回流区也可能会产生杂质沉降现象；此外,在拐角处往往会发生冲蚀现象,影响管道使用寿命。 因此对于弯管流动的准确预测有助于对管道的优化设计和质量把控。

一般可采取实验或者数值模拟的方法对弯管流场进行分析,主要涉及到流场的速度分布、压力分布、回流区大小和分离点等特征。 随着计算机的高速发展,计算流体动力学(CFD)方法的高效、准确和低成本较实验手段有巨大优势［1］。 本文将以CFD 方法对弯管流道进行流动分析,以期获取可信的流场信息及流动规律。

1 方法

1.1 结构建模

如图1 为一典型的R 型弯曲流道,左侧为其三维视图,右侧横截面均为全等的R 型弯曲流道。 流体经由入口流入,经过弯道后从出口流出,由于垂直于流动方向的管道长度相较于流动路径很长,因此该三维问题可以简化成二维流动问题。 只需对图1中右侧所示平面几何进行流动分析,其结果可以代表三维流场中的主要信息。

由于流动雷诺数的变化会导致出口流动状态的改变,为了保证在出口处使流动得到充分发展,随着雷诺数的增大,适当加大拐角后的流道长度,具体几何流场尺寸见图2。 可见雷诺数越大,赋予V2 的值越大,其余尺寸不作改变。

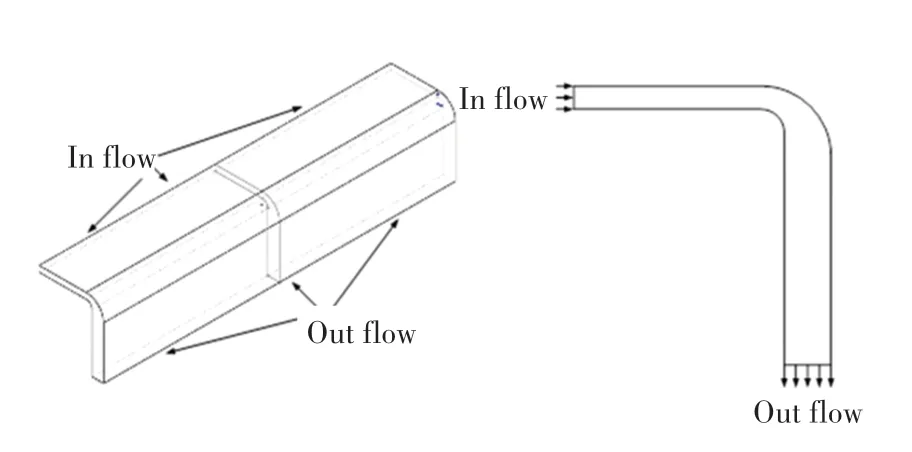
图1 二维剖面图Fig. 1 Two-dimensional cross-sectional view

图2 二维流场Fig. 2 Two-dimensional flow field

1.2 网格划分

在流体力学问题中,流场信息可以通过求解关于流体微团的控制方程得到,对于不可压缩粘性流体建立了N-S 方程。 但对于复杂的外形,直接求解该方程是困难的,因此需要对该方程进行离散处理,寻求数值解。 一般通过对空间的离散处理,即以网格的形式对稳态流场进行求解。 目前的离散方式主要有：有限体积法、有限差分法和有限元法［2］。 目前,ANSYS CFX、ANSYS FLUENT 和OpenFOAM 等都是采用的有限体积法。 本文采取ICEM 对计算域进行网格划分,由于是二维问题且流场区域较规范,故全流域均以四边形网格进行填充。 图3 展示了Re=100 对应几何的以0.2m 作为最大单元尺寸划分的局部流场网格,网格单元总数为1090,以长细比和扭曲度为评判标准的网格质量分别在0.483 和0.527 以上,网格质量较高。

图3 最大单元尺寸0.2m 处的域网格划分Fig. 3 Domain meshing at the maximum element size of 0.2m

1.3 模型设置

本文解决的是不可压缩粘性流体的数值求解,该类问题的控制方程(1)～(3)如下：

其中：p 为流场的无量纲压力,Re 为雷诺数,ν为运动粘度。 式(1)连续性方程,反映了流体质量守恒,式(2)和(3)为动量方程,反映了流体动量守恒。 雷诺数Re 定义为公式(4)：

其中：L 为参考长度,U 为参考速度,μ = ρ·ν,称为动力粘度。 求解时,设定流体密度ρ 为1 kg／m3,参考长度L 为1m,入口处速度为1m／s,方向沿x 轴,且入口处压力设为1 个大气压；两壁面边界均为无滑移壁面；出口为压力出口,表压为零。 由式(4)可知,当雷诺数Re 为100 时,动力粘度μ 应取为0.01 Pa·s。关于Re = 100 时,计算域的边界命名及边界条件设置情况,如图4 所示。 对于管道内流而言,该雷诺数处于层流区间,因此流动模型为Laminar,不考虑流体的传热效应,流体特性及流动模型的设置见表1。 采取SIMPLE 算法对压力和速度进行耦合求解,压力项为二阶格式,动量项为二阶迎风格式,求解方法设置如见表2。

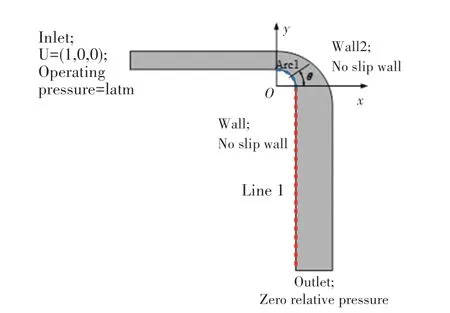
图4 流体域边界条件设置Fig. 4 Setting of boundary conditions of fluid domain

表1 流体域的材料特性Tab. 1 Material properties of fluid domain

表2 求解方法Tab. 2 Solution method

2 结果和讨论

2.1 雷诺数Re ＝100

由上述所给边界条件,设置连续项和速度残差为10 ～6,计算得到了Re = 100 时管道内的静压云图、速度云图、速度流线图、Line1 和Arc1 上静压关于纵坐标的梯度变化。

(1)静压云图。 从图5 可知,最大静压出现在入口处。 在水平阶段,随着流动发展,静压逐渐降低；当流动到达Wall1 拐角处时,静压降至最低；此后流动继续发展,静压又逐步升高,最后达到稳定状态。 另外,当静压梯度由正变为负时,说明发生了分离流动,即图5 中标点所示位置。 Arc1 上静压关于纵坐标的梯度曲线如图6 所示,说明在Arc1 上θ =1.090(62.5°)处发生分离。

图5 Re＝100 的静压云图Fig. 5 Static pressure cloud diagram with Re＝100

图6 静压梯度曲线Fig. 6 Static pressure gradient curve

(2)速度云图与速度流线图。 如图7 所示,随着流动发展,流体速度先增加再减小；处于管道中部的流体速度高于靠近管道壁面的速度,速度最大值出现在管道1／2 径向处,这是由于流的粘性效应,使得贴近壁面处的流体速度为零。 因此,随着与壁面的距离增大,流体速度相应的增大,在距离壁面最远处即1／2 径向处,流体速度达到最大；从图8 可知,在出口附近处的流线已没有回流现象发生,结合速度和静压云图,可以确定在出口处的流动已经充分发展。

图7 Re＝100 的速度云图Fig. 7 Speed cloud diagram with Re＝100

图8 Re＝100 的速度流线图Fig. 8 Speed streamline diagram of Re＝100

图9 Line1 上静压关于y 轴的梯度变化Fig. 9 The gradient of static pressure on Line1 with respect to the y-axis

(3)静压关于纵坐标的梯度变化。 回流点处于静压梯度由负变为正,即如图9 表点所示。 回流区域包含如图8 的螺旋流线,回流长度Lreatt为分离点处弧长与回流点坐标值的绝对值之和,即公式(5)：

式中,θsepar为分离点对应的弧度,yreatt为回流点对应的纵坐标。 因此,Re = 100 对应的回流长度为1.090＋6.693=6.783 m。

2.2 网格独立性试验（仅适用于Re = 100 模型）

在正式计算之前,需要排除网格因素对结果的影响,即要进行网格独立性分析。 针对Re = 100 时的管道流动,建立了5 种类型的网格,分别是coarse, medium, fine, extra＿fine, super＿fine。 他们的区别是最大网格尺寸不同,即代表了5 种不同的网格密度；就aspect ratio 和skewness 而言,这5 种网格的质量处于同一水平；网格具体信息见表3。 图10 中对比了由不同密度的网格计算得到的回流长度,通过左纵坐标可以发现extra＿fine 与super＿fine网格计算结果几乎一致,右纵坐标显示了不同网格的计算迭代步数变化,super＿fine 网格的迭代步数几乎是extra＿fine 的3 倍,为了兼顾计算精确度和计算效率,将采用extra＿fine 类网格进行后续的计算。 比较了5 种不同网格类型下长宽比(Aspect ratio)和偏度(Skewness)的值,如图11 所示,随着网格密度的增加,分离点和回流点的位置均逐渐趋于稳定。

表3 Re＝100 情况下五个网格的信息比较Tab. 3 Information comparison of five grids under Re＝100

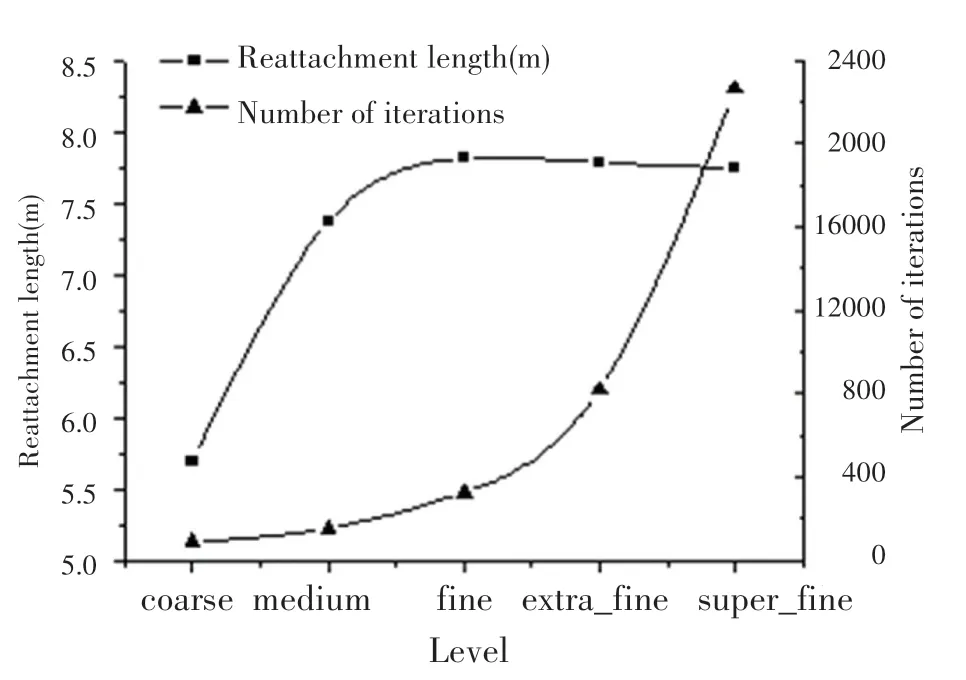
图10 Re＝100 情况下Lreatt的迭代次数和网格独立性测试Fig. 10 The number of iterations and grid independence test under Re＝100

2.3 回流区尺寸相对于雷诺数的变化

讨论不同雷诺数对回流区域的影响。 首先要保证当雷诺数增大时,管道几何要保证在出口处的流动是充分发展的。 通过观察不同雷诺数下管道内的静压云图、流线图和速度云图等变化,判断经过拐角后的流动到出口附近时是否已经得到充分发展。 如图12 所示,不同雷诺数下,压力分布不同,在同一标准图例下可以得到以下几条结论：

(1)随着雷诺数的增大入口处的压力逐渐降低；(2)雷诺数越大,拐角分离点处的角度越大；(3)分离点随雷诺数增加而越来越接近；(4)出口处附近的压力分布均已平稳。

图11 Re＝100 情况下θsepar和yreatt的网格独立性试验Fig. 11 Grid independence test of sum under Re＝100

图12 Re＝50， 100， 150， 200 情况下分别的压力云图Fig. 12 Pressure cloud diagrams when Re＝50， 100， 150， 200

此外,还对比了不同雷诺数下的速度云图,如图13 所示,可以得到以下结论：(1)随着雷诺数的增大,速度场中能达到最高速度的区域越大；(2)出口附近区域的流动速度分布已经稳定。

图13 Re＝50， 100， 150， 200 情况下分别的速度云图Fig. 13 Velocity cloud diagrams when Re＝50， 100， 150， 200

最后,对比了不同雷诺数下的流线图,如图14所示,发生回流的区域随雷诺数增大而增大,可以清晰地看到,在出口附近的流线已均匀分布,达到稳定状态。 结合压力云图和速度云图,可知本文选区的随雷诺数变化而变化的几何可以满足在出口处达到稳定流动的要求。

图14 Re＝50，100，150，200 的流线图Fig. 14 Streamline diagram of Re＝50，100，150，200

为了比较不同雷诺数下的回流长度,将四组分离点和四组回流点随雷诺数的变化曲线分别放到了同一张图里。 图15 显示的是四组雷诺数下的分离点对比图。 可见,当Re = 50 时,分离点所处的角度最小,即最靠近Line1；Re = 100, 150, 200 时,对应的分离点很接近,可以认为几乎不发生变化,大约都在64°附近；Re = 150, 200 时,流动分离前,压力梯度会出现震荡,说明此处的流动情况较为复杂,如果要得到分离前的流场详细信息,可以在该处进行网格加密。 图16 是回流点的对比图,可知随着雷诺数的增大,回流点越靠近出口；且当Re = 100, 150,200 时,在回流发生之前,压力梯度均有类似的震荡现象出现,说明在该区域的流动较为复杂；回流发生后,压力梯度均不再有明显变化。 结合式(5)可得到回流长度随雷诺数的变化曲线,如图17 所示,回流长度随雷诺数增加而增加。

图15 Re＝50，100，150，200 的分离点对比Fig. 15 Comparison of separation points with Re＝50，100，150，200

图16 Re＝50、100、150、200 的回流点对比Fig. 16 Comparison of reflow points with Re＝50， 100， 150， 200

图17 回流长度随雷诺数的变化Fig. 17 Variation of backflow length with Reynolds number

2.4 利用CFD 模拟结果导出预测数学模型

四组不同雷诺数下的回流长度,具体取值如表4 所示。

表4 四组回流长度值Tab. 4 Four groups of return length values

假设这四组值具有三次函数关系,即以雷诺数为自变量,以回流长度为因变量,可设该函数关系为式(6)：

其中,ai(i=0,1,2,3) 为未知系数,x 代表雷诺数,f(x) 代表回流长度。 经过简单的三次函数拟合后得到的各系数为：

可以预测到,当Re = 160 时的回流长度为f(160)= 11.786m。 表5 比较了Re=80, 120, 160时回流长度计算值和拟合值的误差,误差均在1.23%左右。 可见该拟合公式能较好地预测雷诺数与回流长度的关系。

表5 回流长度计算值与拟合值比较Tab. 5 Comparison of calculated value and fitted value of reflux length

3 结束语

通过对三维长流道的简化得到了该模型的二维特征面,使用前处理工具ICEM 对其进行网格划分,应用商业软件FLUENT 对本案例进行计算,使用后处理软件TECPLOT 绘制压力云图、速度云图和流线图。 为了尽可能降低网格对于计算结果的影响,对Re = 100 时的网格进行了独立性检验,结果表明当最大网格尺寸取为0.05 时,能兼顾计算精度和计算效率。 为了保证在出口处的流动已经充分发展,对于流动雷诺数较大的情况,适当增加出口流道长度。 通过提取求解结果中的压力梯度值,分析得到流动的分离点和回流点,进而获取回流长度。 通过雷诺数Re = 50,100,150,200 时的回流长度值,拟合了回流长度关于雷诺数的三次方程公式,并预测了Re=160 时的回流长度。 通过研究,得出点结论：

(1)最大静压出现在入口处,在水平阶段,随着流动发展,静压逐渐降低,当流动到达Arc1 拐角处时,静压降至最低,此后流动继续发展,静压又逐步升高,最后达到稳定状态；

(2)随着流动发展,流体速度先增加再减小,处于管道中部的流体速度高于靠近管道壁面的速度,速度最大值出现在管道1／2 径向处；

(3)随着雷诺数的增大,入口处的压力逐渐降低；

(4)雷诺数越大,拐角分离点处的角度越大；

(5)分离点随雷诺数增加而越来越接近；

(6) Re=150,200 时,流动分离前,压力梯度会出现震荡；

(7) Re = 100, 150, 200 时,在回流发生之前,压力梯度均有类似的震荡现象出现；

(8)拟合得到的公式能较好的预测其他雷诺数对应的回流长度。