湘教版《直角三角形的性质（II）》线上教学设计

陈天宇

【学习目标】

1.掌握直角三角形的性质定理（勾股定理）。

2.学会用勾股定理解决简单的问题。

3.经历探究勾股定理在实际问题中的应用过程，感受勾股定理的应用方法。

【学习重难点】

重点：1.探索并掌握直角三角形勾股定理。2. 勾股定理的应用。

难点：1.勾股定理的证明。2.实际问题向数学问题的转化。

【教学思路】

本节内容采取“自学——引导分析——线上答疑——作业”的方式进行学习，在同学们自学课文后，根据问题引导学习分析，进一步理解新知识，认真完成练习，然后进行线上答疑，让同学们真正掌握所学内容。

【教学过程】

一、自学课本内容，完成学习任务：（导学案通过微信班级小管家提前发给同学们，希望在规定时间内完成）

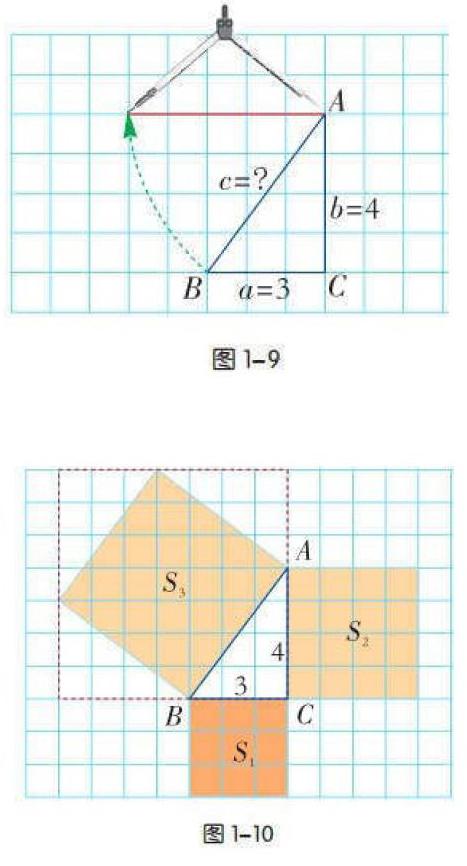
（一）阅读课本第 9 页中的做一做，根据图 1-9 发现问题。

1.你量得AB的长是___________________________________________。

2.然后分别算出（AB）2、（AC）2和（BC）2 的值，你发现了什么？

（二）阅读课本第 9 页中的议一议：根据以下问题引导分析，猜想结论。

1.图1-10 中的正方形S ₃的面积如何计算？ 得S ₃的值为____________，（AB）2的值为

2.由此猜想，你会得出什么结论？

二、独立探究勾股定理

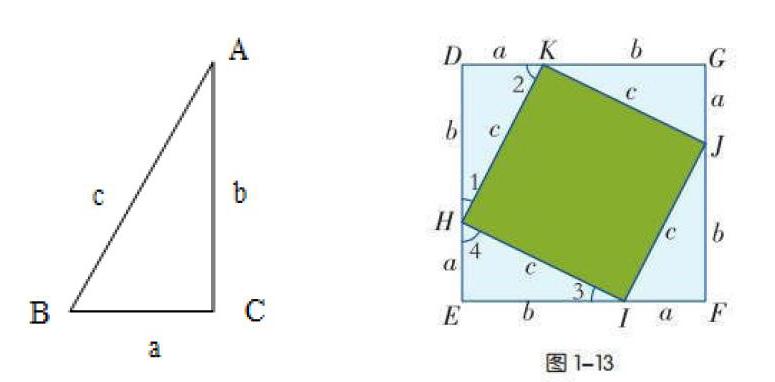
如图，任作一个 Rt△ABC，∠C=90°，若 BC=a，AC=b，AB=c，那么 a2+b2=c2 是否成立呢？

先阅读课本第 10 页的探究步骤，动手实践，得到如图 1—13这样的图形，并根据以下问题引导推理，得出勾股定理。

（一）在图 1-13 中，点D、H、E为什么在一条直线上？

（二）四边形DEFG的边长等于a+b，由此得四边形面积为____________ 。

（三）四边形DEFG的面积又等于哪几个图形的面积和？

由这几个图形的面积和所算得的四边形面积为_______________________ 。

（四）由上面2和3所算得的四边形面积相等吗？得相应的等式为____________ 。

三、练习：勾股定理的应用（同学们完成后，在规定时间内拍照上传到微信班级小管家）

1.在 Rt△ABC中，∠C=90°，

（1）已知 a=25，b=15，求 c;

（2）已知 a=5，c=9，求 b.

2.在等腰三角形 ABC 中，已知 AB=AC=13cm，BC=10cm，AD⊥BC 于点 D，你能算出 AD 的长吗？

四、线上答疑

（在线上教学时间，利用班级数学学习微信群，或者 QQ 群进行线上答疑，解答同学们在练习上出现的错误及提出的问题）

五、归结反思

说说你在本节内容的学习上有什么收获和疑惑？

六、线下作业（同学们完成后，拍照上传到微信班级小管家）

1.在 Rt△ABC 中，∠C=90°，

（1）若a=3，c=5，則b= ____________________________________________________________;

（2）若a=5，b=12，则c=____________________________________________________________;

（3）若c=25，b=7，则a=____________________________________________________________;

（4）若a=8，b=15，则c=____________________________________________________________ 。

2.已知一个直角三角形的两边长分别为3和4，则第三边长是 _________________________________________________________________________________。