“无所不能”的合力矩定理

刘小妹 梁拥成

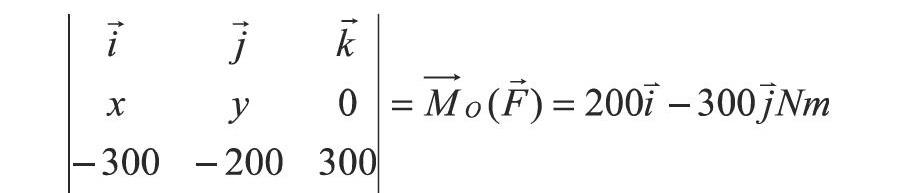
摘 要 基于合力矩定理分解的思想和合力矩定理解析式的应用两个方面，对合力矩定理作了一些归纳和总结，例举说明了定理在力学中的“无所不能”的作用：利用其分解的思想直观方便求力矩，力偶;利用解析式求平面任意力系、空间任意力系、空间平行力系合力的作用线位置。

关键词 理论力学 合力矩定理

中图分类号：O312.1                                   文献标识码：A    DOI：10.16400/j.cnki.kjdks.2020.09.032

Abstract Based on the idea of decomposition of resultant moment theorem and the application of analytical formula of resultant moment theorem， this paper sums up the theorem of resultant moment， and illustrates the omnipotent function of the theorem in Mechanics： it is intuitive and convenient to find moment and couple by using its decomposition thought; and it is used to calculate the resultant force of plane arbitrary force system， spatial arbitrary force system and spatial parallel force system line position.

Keywords theoretical mechanics; theorem of moment of resultant force

0 引言

在理论力学静力学这一大篇中，对于力系主要研究了合成与平衡两大问题。关于合成有合力投影定理和合力矩定理。这两个定理在静力学中具有重要的作用，比如合力投影定理在汇交力系中，可以求合力的大小和方向。实际上，合力投影定理适用于任何矢量比如在运动学中的速度和加速度。点的合成运动和刚体平面运动中求速度与加速度矢量合成，本质其实就是合力投影定理的推广。在任意力系中合力投影定理可以求主矢的大小和方向，但是合力作用线位置，还必须借助于合力矩定理。利用合力矩定理可以求得主矩的大小，进而求得合力作用线的位置。这两个定理，在汇交力系、平面任意力系、空间任意力系中均分别作了叙述和证明，繁锁而又重复。事实上这两个定理 均无需证明， 而可直接由合力的定义得出。[1]平面问题，力对点之矩，实际上空间问题中的力对轴之矩，是一个代数量，而在空间问题中，力对点之矩是一个矢量，合力矩定理在两种情况下都是成立的。因此总的来说合力矩定理是指合力对任一点之矩矢等于力系中各力对该点之矩矢的矢量和;合力对任一轴之矩等于力系中各力对该轴之矩的代数和。

纵观力学教学过程，很多地方都应用了合力矩定理。在静力学中无论是求力对点力矩，一般任意力系的合成或是平行力系的合成都经常会用到合力矩定理，因此合力矩定理的应用是力学教学中的一个重点内容，应该加以重新的认识和重视。刚开始是利用合力矩定理的分解思想纯粹求力矩，然后把合力矩定理中的作用点坐标看作是力的作用线上的任意一点，可以求任意力系的作用线方程，最后还可以用合力矩定理求平行力系的中心。在教学过程中应该引导学生不断地对合力矩定理加以新的认识，让学生在一步步深入学习的过程中，不断强化理解合力矩定理，学生自然而然地就掌握了它的意义。本文基于合力矩定理分解的思想和合力矩定理解析式的应用两个方面，对合力矩定理作了一些归纳和总结，通过实例，说明了该定理在力学中的“无所不能”的作用。

1 合力矩定理分解的思想的应用

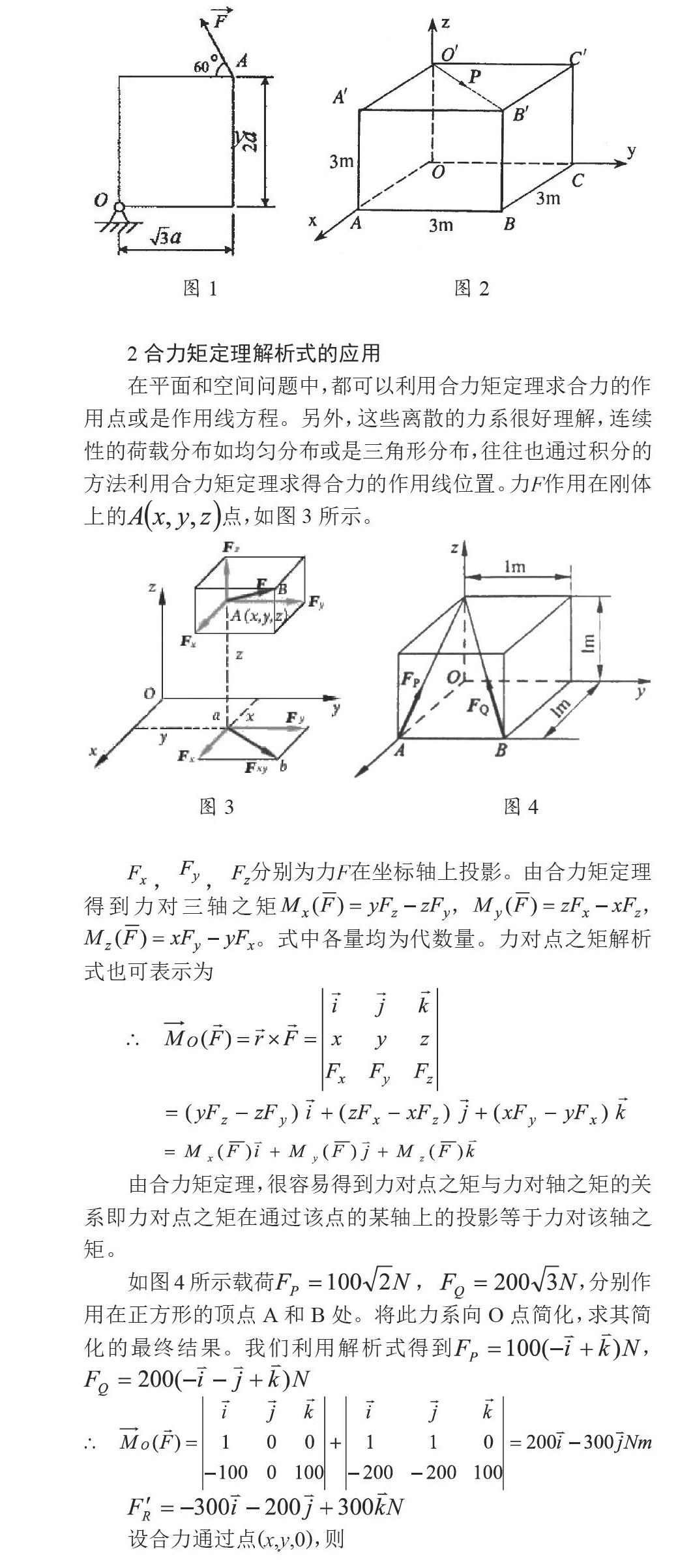
求力对点之矩，听起来很简单，但是由于学生起初学力矩时就是用力乘以力作用线到该点的距离，由于先入为主，学生一遇到求力矩，就想到求距离，但是在理论力学求力对点之矩时，一般距离不太直观方便，这时，我们可以依据合力矩定理先把力分解，分别求每个分力的矩，然后合成，这不仅适用于平面，也适用于空间，也适用于求力偶矩。例如在图1中矩形板的A点处作用一力，方向如图所示，则该力对点O的矩。如果直接求力的作用线到O点的距离，不太直观，我们可以先在力作用点处A将力先分解水平和竖直的分力，这样很容易直观看出水平和竖直分力到固定点O的距离分别为和，依据合力矩定理，两者分别产生的矩的代数和为。

再例如在空间力系图2所示立方体，长、宽、高均为3m，沿对角线O′B有作用力P=10kN，如果要求此力对、、轴之矩，我们也可以先在作用点处O点把作用力分解成、方向上的分力，然后在求所有分力对、、轴之矩的代数和。

2 合力矩定理解析式的应用

在平面和空间问题中，都可以利用合力矩定理求合力的作用點或是作用线方程。另外，这些离散的力系很好理解，连续性的荷载分布如均匀分布或是三角形分布，往往也通过积分的方法利用合力矩定理求得合力的作用线位置。力作用在刚体上的点，如图3所示。

这也适用于平行力系，得到平行力系的中心，进而得到重心，形心的位置。特别地，求形心的位置，与材料力学当中的静矩之间有内在联系。材料力学中物体的静矩学生觉得概念比较抽象，但是静矩叫面积对轴的一次矩，学习的时候，可以把静矩和力矩有机结合起来。同理可推广至惯性矩，故而得到了在稳定中的惯性半径的概念，可见面积对轴的二次矩， 也可视为面积集中于惯性半径位置处的二次矩，这些分分合合中体现了化繁为简的重要思想。[2]

3 结论

在力学教学过程中，讲解合力矩定理内容时，虽然对该定理本身的证明，理解一点都不困难，但是发现他的应用还真不少，有时候要利用其分解的思想来求力矩，力偶，抛弃原有的固定思维求距离，有时候还可以利用解析式求合力的作用线位置，平行力系中心。很多同学在一开始学习时，总认为求合力，只是其大小和方向，其实还有一个很重要的要素就是作用点，或是作用线，这就要发挥合力矩定理的“无所不能”的作用了。本文对合力矩定理作了简要的概括和总结，其实合力矩定理还连接了理论力学和材料力学的桥梁，那就是截面的静矩，在教学过程中，把所学的内容加以归纳总结，做到知识的融会贯通，理解就会深刻。

参考文献

[1] 李克安.有关工程力学几个问题的讨论[J]岳阳大学学报，1988（2）：89-93.

[2] 邹思敏.横看成岭侧成峰——浅议合力矩定理在土建工程中的应用有关工程力学几个问题的讨论[J].建材发展导向，2017：393.