宏观角度对福建省就业影响因素的分析与探讨

一、前言

众所周知，充分就业是每一个国家都必须面对的热点问题，同时也是每个国家重要的经济发展目标。世界上各个国家的就业状况并不容乐观，时有波澜。而我国就业形势虽然也面临着重大的挑战，但是在经济高速发展之下，新增就业岗位数得到快速增长，仅针对福建一省所收集到的20年数据来看，就业人数增长迅速，有着显著的上升趋势。福建的地理位置比较特殊，它位于我国的东南沿海，是长江三角与珠江三角的连接点，并且与台湾相隔不远，因此，福建省在我国经济发展中也有着特殊的战略地位，对福建省就业影响因素的研究就显得尤为重要。

针对我国的现状、福建省的现状，建立一套对于就业人数的科学的预测体系是把握住控制就业的主动性的前提。因此，本文想收集大量的历史数据，通过利用统计学的知识与R语言科学地分析福建省就业的影响因素，建立回归模型，进而对就业人数进行预测，并将预测的结果与现实情况进行对比，判断模型是否有效。

查阅相关的资料，可知影响就业人数的主要因素有：地区生产总值、每万常住人口拥有的在校大学生数、人口自然增长率、税收、教育支出。本文将这些因素作为变量、就业人数作为因变量，对二十余年的具体数据建立回归方程，进行多重共线性、异方差、自相关的检验与消除，用最后确定的模型进行对就业人数的预测，对比分析结果，解释其中存在的互动关系。最后初步进行总结，提出相应的政策建议，以促进福建的就业人数的增长，优化就业结构，营造良好的就业环境，以实现充分就业的经济发展目标。

二、模型与求解

（一）数据

使用数据为1997-2007年福建省就业相关数据，共21条。包括5个自变量变量（地区生产总值、每万常住人口拥有在校大学生数、人口增长率、税收、教育支出）和一个因变量（就业人数）。数据来自《中国统计年鉴》《福建统计年鉴》（1997年至2017年）。

利用R语言将数据导入并得到散点图。由散点图可见x1地区生产总值、x2每万常住人口拥有在校大学生数、x3人口自然增长率、x4税收、x5教育支出与y就业人数基本呈线性关系，所以初步可以建立方程。

（二）线性回归

初步建立回归模型可知x1、x2与x4对y起正影响，x3与x5对y起负影响，这与定性分析结果显然不一致，从数据可直接看出这5个变量对y都起正影响，原因可能是自变量数目太多，变量之间存在着相关关系。

给定显著性水平为0.05，x3相应的p值为0.103234，没有通过回归系数的显著性检验，说明x3对因变量的影响不显著。决定系数为0.9949，从相对水平上看，回归方程能解释因变量y的99.49%的方差波动。回归标准差为35.95。回归模型的F值为585，p值＜2.2e-16，由此可知回归方程整体上高度显著，这与相关系数的检验结果是相一致的。

（三）多重共线性诊断与消除

多元线性回归模型的一个基本假设即设计矩阵X的秩rank（X）=p+1。即要求各解释变量之间线性无关。而这一假设在实际问题中却是常常难以满足的，比如在该研究问题中，涉及了5个自变量，自变量的数目比较多，并且很难从其中找到一组自变量，它们之间是完全不相关的关系。在实际的问题中，如果一个经济社会现象受到多个重要的因素影响时，这些解释变量之间往往有一定的相关性。当解释变量的相关性比较弱时，我们可以认为近似满足多元线性回归模型的基本假设；当一组变量之间的相关性比较强时，就认为违背了基本假设。

x1，x2，x3，x4，x5之间的相关系数很高，且在第三步线性回归中，x3与x5的回归系数正负号与定性分析结果相违背，这初步说明了该模型有多重共线性。这与基本预测是相一致的，当所研究的经济社会问题是关于时间序列的资料时，由于这些变量随时间往往有着相一致的变化趋势且关联密切，多重共线性的问题很难避免。因此进行逐步回归，并且按照AIC准则删去多余变量，对剩下变量做回归。

从输出显著性结果可看出，当保留x1，x2时，各参数t检验通过，说明模型拟合较好。决定系数为0.9913，从相对水平上看，该模型能解释因变量y的99.13%的方差波动。回归标准差为42.92。从方差分析表中可以看到，回归模型的F值为1023，p值＜2.2e-16，由此可知回归方程整体上高度显著。

因此，最终方程为y=1422+0.03387x1+1.656x2。

（四）异方差检验及自相关检验

现实中的问题是充满复杂性的，对于此类问题进行回归分析时，往往其中的某些因素随着解释变量观测值的变化，而对被解释变量产生复杂的影响，导致随机误差项产生不同的方差。当一个回归问题存在异方差时，常常会破坏模型的有效性，因此本模型中需要对异方差进行检验。

异方差的检验结果可看出，P=0.05638>0.05，说明模型不存在异方差。

在时间序列中，往往会出现正的序列相关。而建立线性回归方程的一个基本假设就是其中的随机误差项不存在序列相关。因此，诊断随机扰动项是否存在自相关性，对于问题的研究和模型的建立是一个重要的方面。

对模型进行自相关的检验，可得P=0.1812>0.05，因此该模型不存在自相关。

三、模型检验

（一）残差图与回归散点图

一个模型通过了t检验或者F检验并不能够确保这个模型是有效的或者这个模型对数据拟合得很好，只是说明解释变量与被解释变量之间有比较显著的线性关系。还时可能存在其他的一些问题导致数据并不可靠。比如异常值与周期性干扰。残差值是实际数据与通过回归方程得到的回归结果之间的差值。只有通过检验残差项相关的检验，才能够保证回归模型的正确性可靠性。因此在以下的步骤中，通过使用残差图，来判断模型的效果与质量，检验基本假定是否满足。

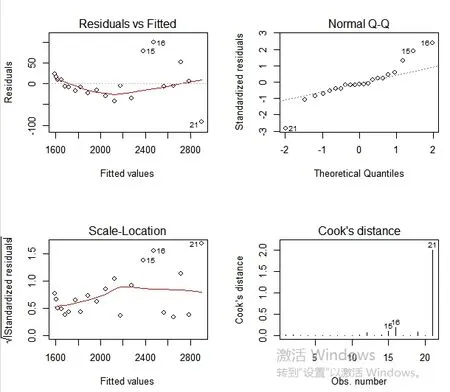
图1 残差图与回归图

图1可以看出，第15、16、21样本点显然出现了不同程度的偏离，因此可以将这三个点看做异常点。在接下来的步骤中进一步确定这三个点是否存在问题。

（二）正态性检验

如果残差是正态分布，那它就是具备着随机性的，进一步可以看做比较好的拟合了随机误差。

对残差进行正态性检验可得，P=0.1046>0.05，说明模型的残差是正态性的，满足了线性回归模型的假设。

四、模型预测

利用R语言对建立的模型求得预测结果与预测区间。将预测输出结果与实际数据做对比分析，发现实际的数据都落在预测区间内，因此表明此模型的拟合效果很好。

五、结论与对策建议

（一）结论

最终得到的结果模型为：y=1422+0.03387x1+1.656x2。

可以看出，在其他变量不变的情况下，地区生产总值每增加1亿元，就业人数增加0.03387万人；每万常住人口拥有大学生数每增加1人，就业人数增加1.656万人。

（二）政策建议

通过对福建省就业因素的研究可以看出，从宏观经济来讲，地区生产总值会对就业人数的上升起到积极的影响。当社会开始出现经济衰退、生产消费不振时，常常伴随着失业人数增加、劳动力供给水平降低的情况。政府在就业问题中起着关键的作用，科学有效的财税政策对于社会经济发展起到重要的指导作用。政府需要扮演好自己的角色，掌控好宏观经济，才能保持经济稳定增长与繁荣，促进社会发展，最大程度降低失业率，实现充分就业。从发展产业来看，短期内就业增长最有效的方式是把重点放在劳动密集型企业，以此增加人民就业；而从长期来看，技术与资本密集型企业是经济发展的最大带动力，以此才能在这个科技高速发展的时代保持长期稳定的经济繁荣。在政策制定时应该二者兼顾，做好短期与长期的有机链接，将经济增长与带动就业更好的结合起来。

除了社会宏观经济方面的影响，每万常住人口拥有的大学生数也是就业增长的一个重要因素，从中体现出来的是教育问题、人才培养问题。政府部门应该考虑加大对教育方面的财政投入，对教育结构进行科学的调整，引导社会各界的力量去促进教育的发展，切实提高教育质量。除此之外，政府也应该考虑到教育资源分配不协调的问题，现如今，寒门越来越难出贵子，教育资源应该往农村地区贫困地区有所倾斜，保证贫困家庭孩子也能接收到高质量的教育，这是促进贫困地区弱势群体经济内生增长的有效方式。