一种基于时间序列分析的赤潮预测新方法研究——以浙江海域为例

徐丽丽，余骏，高鑫鑫 ，车助镁，何雯 ，邱婷

（1. 国家海洋局东海预报中心，上海200081；2. 海洋生态监测与修复技术重点实验室，上海200081；3. 浙江省海洋监测预报中心，浙江杭州211800）

1 引言

赤潮又称红潮，国际上也称为“有害藻华”或“红色幽灵”。赤潮已成为当今世界普遍关注的海洋生态问题[1]。我国于2005 年制定了《赤潮海洋灾害应急预案》并实施至今，赤潮灾害预测及评估工作被列为政府工作报告内容之一；各级海洋减灾相关部门和预报业务机构建立了赤潮年度预测和月及周会商业务制度，作为我国政府赤潮灾害应急决策和处置的工作依据和技术支撑。我国浙江海域受南下长江冲淡水、北上台湾暖流、钱塘江和瓯江等径流注入以及外海上升流系的综合影响，其环境极有利于赤潮生物的生长繁殖。国内最早的赤潮记录是1933 年费鸿年记载的浙江镇海至台州-石浦一带的夜光藻和骨条藻赤潮[2]。根据1989——2019年《浙江省海洋环境公报》和相关文献资料[3]，浙江海域在1981——2019 年间共记录到赤潮事件744 次，累计面积超过1.74×106km2。尤其进入21 世纪以来，超过上千平方公里的浙江海域内，大型赤潮和有毒赤潮都呈明显增长趋势。这不但对人民生命健康与海洋生态环境造成了极大威胁，同时也成为浙江省海洋经济高质量和可持续发展的一个重要制约因素，因此引起我国学者和各级政府的高度关注。

至今，学术界已对赤潮发生过程的模拟预报和赤潮灾害趋势或概率预测等做了大量研究。但因赤潮爆发原因复杂，各藻种及种间发展的生态机制尚不完全清楚，现有的预测研究从开始的主要基于气象水文等因子的定性分析和条件预报[4-5]，逐渐发展到利用连续赤潮现场监测或遥感数据[6-8]、基于主成分和多元回归等统计模型做预测[9-10]。但在实际业务应用中，这些方法受限于样本数据、变量因子的敏感性等因素，从而影响预报精度乃至难以做出有效预测。随着监测数据的丰富和某些赤潮种生态规律机制研究的深入，部分学者开始利用物理-化学-生物耦合的生态动力学数值模型进行赤潮模拟研究[11-17]。如夏综万等[16]考虑生物动力学和环境动力学因素，建立了大鹏湾夜光藻赤潮生态仿真模型；李雁宾[17]对长江口及邻近海域季节性的赤潮生消过程控制机理进行了研究。生态动力学数值模型可以对机理明确、变量初始值及边界条件来源详尽且连续的局部海域做某个具体赤潮过程的模拟预测，但在以年为尺度的业务化预测上的应用效果有限。近年来，以神经网络和深度学习为代表的大数据预报技术飞速发展，其在非线性模式识别方面具有独特的信息处理和解算能力，非常适用于赤潮这种机制尚不清楚的高维非线性系统[18-19]，但其对数据要求量大、质量严格且建模过程复杂。以上是赤潮预测研究取得的众多成果，在业务化应用中也取得一定成效。但由于赤潮爆发受到水文气象条件、海水理化因子变化以及船舶带来的外来浮游物种入侵等众多因素的影响，加之赤潮生态系统各因子间表现出的高度非线性和不确定性，以及连续监测数据获取困难等问题，目前在一线业务预报机构中能真正使用，且满足实际业务工作需求的赤潮预报工具箱的选择还不够多。尤其是针对东海区浙江海域的业务化赤潮预测研究主要以定性分析为主[20-23]，业务一线应用的定量预测方法基本空白。

为满足自然资源部东海分局及浙江省监测预报中心赤潮年度预测和月会商的业务需求，并规避数据限制和机理研究要求，本文拟基于1981——2018年浙江海域赤潮月发生次数构建时间序列；考虑赤潮长期的年代变化特征又兼顾其季节性生态变化规律，提出一种基于自回归移动平均（Auto Regressive Integrated Moving Average，ARIMA）模型的时间序列模型，以及易于实现且便于使用的赤潮预测新方法，为浙江海域的赤潮灾害年度预测、业务化赤潮预警报和灾害评估工作提供新的技术工具。

2 数据与方法

2.1 数据来源

赤潮原始数据来源于自然资源部海洋预警监测司发布的1989——2019 年《中国海洋灾害公报》及浙江省海洋监测预报中心提供的1981——2019 年的监测数据。具体参数包含赤潮发生时间、发生海域、经纬度、最大记录面积、分布形态、优势藻种、密度和水色，时间跨度为1981——2019年。因赤潮发生具有年际、季节和月等不同时间尺度变化，如果直接利用原始时间序列数据构造模型，容易因非平稳特性产生虚假回归，因此整理并建立38a 浙江赤潮发生频率的时间序列后，先对其进行平稳化处理。

2.2 分析方法

时间序列分析法是根据一组相依有序的离散数据，建立反映时间序列中所包含的动态依存关系的数学模型，并进行未来状态预测[24]。对于非平稳时间序列，主要运用ARIMA 模型，亦称Box-Jenkins模型。指定3 个参数，即描述自回归阶数（p）、差分次数（d）和移动平均阶数（q），模型通常被写作ARIMA（p，d，q）。其数学表达式为：

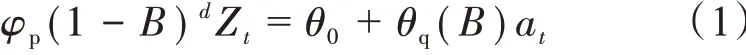
式中：Zt为原序列；at为白噪声序列，是一列相互之间无关、均值为0、误差的方差为σ2的随机变量序列；B 为后移算子即BZt= Zt-1；φp为自回归算子，φp( B ) = (1 - φ1B - …- φPBP)，P 为模型的自回归除数；θq为移动平均算子，θq( )B = (1 -θ1B - …- θqBq)，q 为模型的移动平均阶数；θ0为参数，θ0= μ(1 - φ1- φ2- …- φp)，μ为平均数。

建立模型前需根据时间序列的特性（平稳性、非平稳性和季节性）确定建模类型。若序列非平稳且有季节性，则模型函数被记作ARIMA（p，d，q）（P，D，Q）s。它可以用于分析不仅含有季节性成分、还混有非季节性成分的时间序列资料。其中（p，d，q）和（P，D，Q）分别为非季节性和季节性自回归（Auto Regressive，AR）、差 分（I）和 移 动平 均（Moving Average，MA）的阶数，s代表季节周期。本文中模型的原始序列平稳化、模型参数估计、模型诊断和预测均借助SPSS 25.0 统计分析软件，采用编程法（语句）分析处理。建模过程见图1。分3 个关键阶段[25]：（1）模型参数的确定。利用自相关和偏自相关分析时间序列原始数据的随机性、平稳性和季节性，初步确定模型参数p、d、q 及P、D、Q 的取值；（2）模型参数的检验。首先采用Box-Ljung 检验模型白噪声判断模型的拟合优度；若有两个或两个以上的模型通过检验，则根据贝叶斯信息准则（Bayesian Information Criterion，BIC）判断模型类型和最优阶次[26]，具体算法见式（2）和（3）；（3）预测应用。通过对比模型预测值与实际值的差值，评价模型预测的准确性。

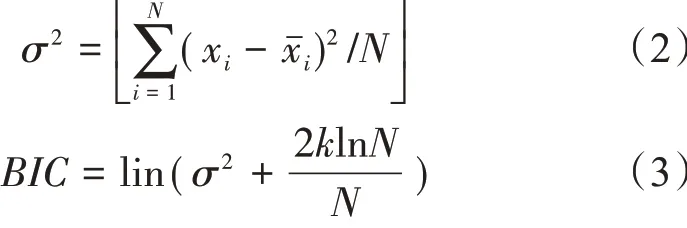
式中：N为样本个数，k为参数估计的数量，σ2为误差的方差。在ARIMA 模型中取BIC 最小值作为评价指标确定p、q以及P、Q值。

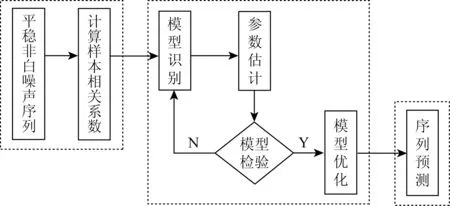
图1 时间序列模型建模具体流程

3 分析与讨论

3.1 序列平稳化处理

根据1981——2019 年共744 起赤潮发生事件可知（见图2），浙江海域赤潮发生次数具有明显的“低频发生-爆发增长-缓降波动”3 段式年际变化特征。20世纪为低频发生阶段：其中80年代发生频次寥寥无几，年均两次；90 年代尤其是前期略有增加，年均4.5 次。进入21 世纪后，赤潮发生次数呈现爆发性增长，高达45 次/a；2003 年到达了历史峰值79 次后逐渐回落。2010 年后进入第三阶段，发生次数缓降后呈稳定波动状态，比前10 a明显减小，年发生数维持在18次/a。

从季节分布来看，一年四季皆有赤潮发生，但集中爆发于春夏两季（发生次数占97.5%）。由图3可知，除11、12月以外，其余各月份均有赤潮发生且主要在4——8 月。其中5 月发生最多（287 次），其次为6月（188次），分别占全年的46.7%和29.7%；发生最少月份为10 月，共发生4 次，约占0.3%。从持续天数来看，浙江海域持续天数1～3 d 的短期赤潮出现次数最多，占64%；20 d以上的超长周期赤潮事件共出现11 次，占1.8%，其中最长持续天数为31 d。值得注意的是两次超长持续时间的赤潮事件发生时 间 段分别为2011 年2 月9 日——3 月7 日 和2017 年2 月7 月——3 月9 日，均发生在冬季的象山港港底海域。相关研究已表明[27]，象山港在电厂建成前冬季平均水温约为8～9 ℃。2005 年底宁海国华电厂和2006 年底大唐乌沙电厂相继投产后，温排水使得附近海域的水温升高，4 ℃温升包络线范围不断扩大使水温达到15 ℃左右的可能性大大增加，而且冬春季温排水的热效应使浮游植物量增加约5%。因此推测由于温排水的热效应导致生物量增加，从而使得象山港海域冬末春初的赤潮呈现低温期爆发、持续时间长、影响面积小等特点。因此，必须重视特殊海域“低温期”的赤潮事件，以防在赤潮预警报业务中“漏报事件”发生。

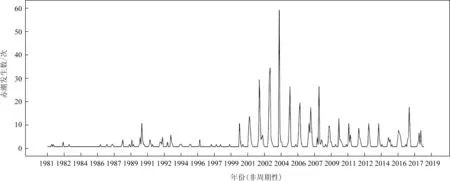
图2 近40 a浙江海域赤潮逐月发生次数时序图

由图2、3 可见，浙江海域赤潮发生次数既存在明显的年际变化，同时也存在典型的季节波动，因此导致基于赤潮发生次数逐月原始数据建立的时间序列非平稳且具有季节性。当变量不平稳时，若直接构造ARIMA 模型容易产生虚假回归，因此须先对原始数据进行一阶普通差分。差分后虽然已没有上升和下降趋势，但是随着时间的增加周期性一直存在，因此还需继续做季节差分。图4显示，一阶季节差分后，序列的长期趋势和季节性趋势基本消失，数值围绕0 上下随机波动。自相关图呈现逐渐衰减的趋势，自相关系数能够趋于0，且延迟16阶后在0 值附近波动，统计量的相伴概率小于0.05，通过单位根检验（ADF）[28]，故可认为处理后的时间序列平稳，符合建模的条件。

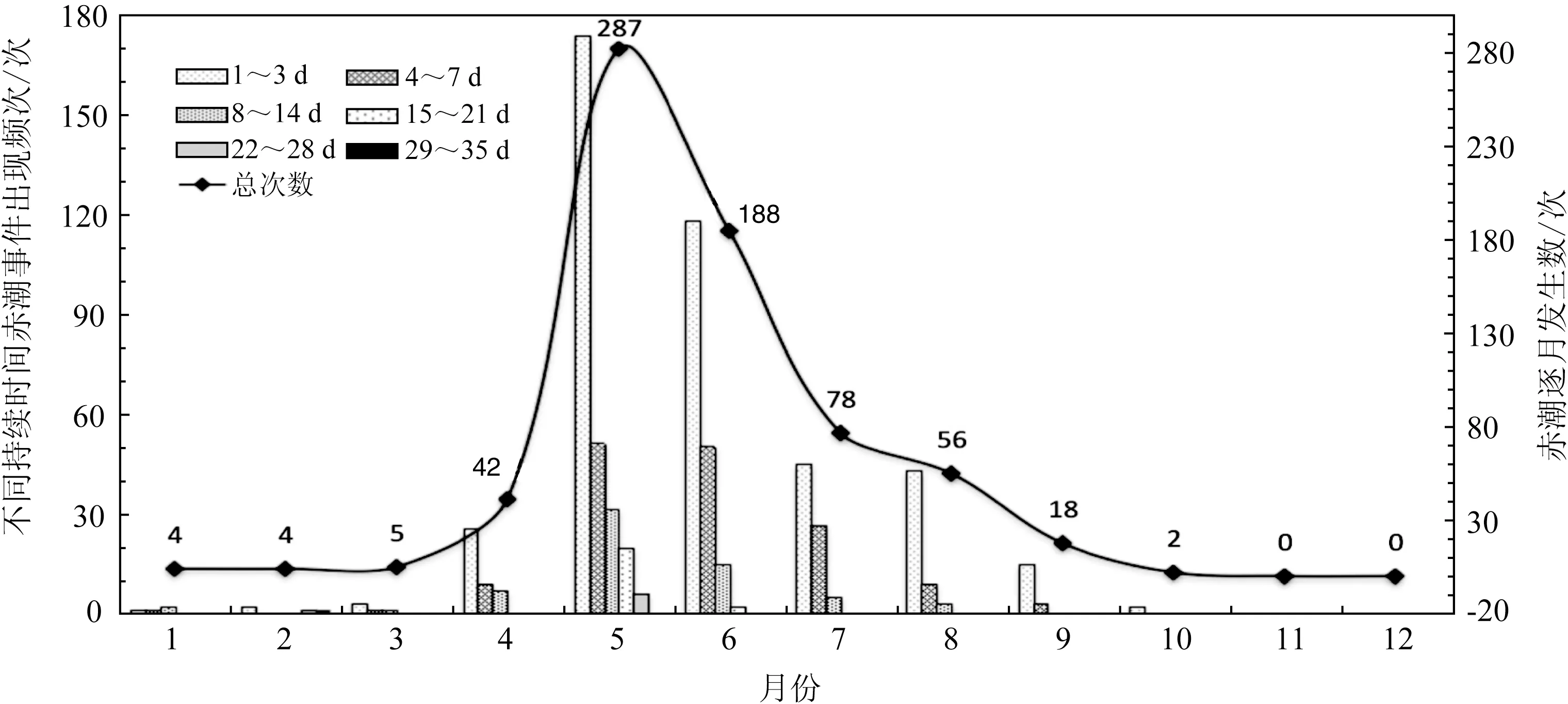
图3 近40 a浙江海域赤潮月发生次数分布特征图

图4 近40 a浙江海域逐月赤潮发生数差分序列图

3.2 模型拟合及参数确定

上文处理后的平稳时间序列，可依据Box-Jenkins的理论方法直接构建ARIMA模型。

根据赤潮发生次数时间序列的差分情况及季节性特征，可以初步判别该时间序列是周期为12的复合季节模型ARIMA（p，d，q）（P，D，Q）s，故S 取值为12；差分后序列自相关系数（Auto -Correlation Function，ACF）和偏相关系数（PArtial Correlation Function，PACF）[29]表明（见图5），ACF和PACF 均在P 参数大于l 后骤减，故初步判断连续模型为RIMA（1，l，1）。季节模型的参数P、Q判断较复杂，一般情况下超过二阶的情况很少见，可以分别取0、1、2 由低阶到高阶逐个实验。本文基于SPSS 25.0 统计软件“时间序列预测”模块中的专家建模器，通过极大似然法[30]进行估计，初步拟定模型参数，剔除系数不显著的模型，并对剩下模型的残差进行Ljung-Box非线性检验[31]，选出P＞0.05 的模型；再从选出的模型中遵从BIC 准则[26]筛选出最优模型。由表1 结果可知，Ljung-Box 的Q 检验显示残差目前并未违反白噪声的假设，也没有出现离群值，选取的赤潮发生次数时间序列的最优预测模型为ARIMA（1，1，1）（1，1，0）12，拟合优度系数为0.68，结果在可接受范围内。图5 可见模型残差的ACF 和PACF 均≤0.5，残差序列各数值间没有相关性，这说明建立的预测模型已充分提取了序列信息，是合适且可信的。

3.3 模型检验及预测讨论

一般情况下，为评估预测模型的稳定性和适应性，会选择拟合优度、平均绝对误差和相对误差来评价模型的整体拟合度[32-33]。因为赤潮逐月发生次数样本的特殊性，大多数样本为0值或数值较小，从而导致绝对误差和相对误差较大，但在实际业务中却属于可接受范围，因此本文采用绝对误差值范围出现概率作为评价指标。基于上文建立的最优模型ARIMA（1，1，1）（1，1，0）12，对1981 年1 月——2018年12月的赤潮逐月发生次数进行模拟计算，模型拟合优度系数为0.68，模拟值与实测值较吻合（见图6）。

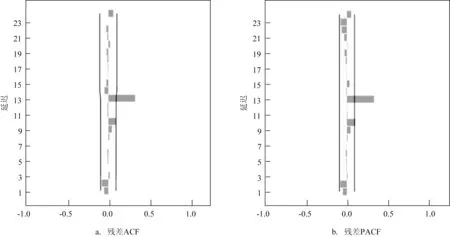
图5 残差的ACF和PACF图

表1 浙江海域赤潮发生次数ARIMA预测模型的相关参数

ARIMA 模型中，数据样本的时间尺度以月为单位进行计算。744 次赤潮发生事件按照实际发生时间归入各月中，形成ARIMA 模型的457 个样本。由表2 可知，在457 个样本中，绝对误差控制在两次以内的样本共382 个，占总数的84%；其中绝对误差为0 次即模拟值与实测值完全吻合的月份有292个，占比64%。但也存在个别月份绝对误差较大的情况，主要出现在2000——2005年浙江海域赤潮爆发性增长阶段，尤其是2004 年5 月赤潮发生次数爆发性增长至峰值59 次，ARIMA 模型未能准确拟合这种超历史极值的小概率异常情况。

利用上文建立的模型对浙江海域2019 年赤潮逐月发生次数进行预测（见图7）。2019年浙江海域赤潮实际发生次数为22 次，预测值为19 次，赤潮年发生次数的相对误差为14%。其中4 月、5 月和8 月的绝对误差都控制在两次以内，其余月份预测值与实测值完全吻合（见表3）。 可见本文建立的ARIMA 模型能够较准确地进行赤潮发生次数的年度趋势预测。

图6 赤潮逐月发生数ARIMA模型预测值与实测值对比

表2 ARIMA模型模拟值与实测值的绝对误差统计

图7 浙江海域2019年赤潮逐月发生次数预测

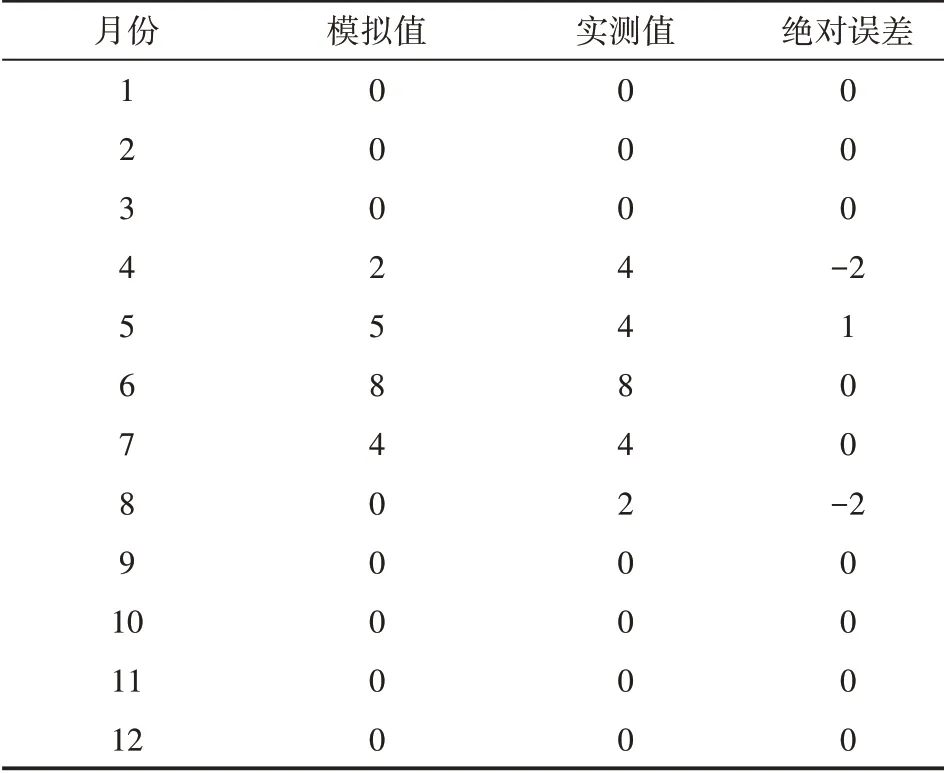
表3 浙江海域2019年赤潮逐月发生次数预测值与实测值的绝对误差统计

4 结论

考虑赤潮系统的高维非线性机制和年度预测业务需求，本文利用近40 a 浙江海域赤潮逐月发生次数的时间序列，分析其在年际、季和月3个不同时间尺度的变化特征；通过对原始序列的差分处理，基于时间序列分析方法建立了ARIMA 预测模型，并对2019 年浙江海域赤潮逐月发生次数进行后报和检验。结果如下：

（1）浙江海域赤潮发生次数存在明显年际变化特征，经历了“低频发生-爆发性增长-缓降后波动”3个明显的阶段，其中2000 年和2010 年为转折点。同时也存在典型的季节波动，97.5% 集中爆发在春、夏季，其中每年的5 月发生最多，共298 次，占全年的46.7% 。从持续天数来看，1～3 d 的短期赤潮出现次数最多，占64%。

（2）通过对原始序列的差分处理和参数检验，最终建立ARIMA（1，1，1）（1，1，0）12模型且残差通过白噪声检验，拟合优度系数为0.68，绝对误差控制在两次以内的样本占总数的84%。用此模型对浙江海域2019年赤潮发生次数进行预测，后报检验显示年发生总次数相对误差为14%，各月绝对误差均在两次以内，预测结果与实际较吻合。

（3）时间序列预测法需要的仅是序列本身的历史数据，对机理研究没有高要求，在赤潮年度预测等业务中具有简易实用且经济性好的优势；同时在具备长时间序列数据的基础上，其精度在业务应用可接受范围内。在今后的相关研究中，可探索线性与非线性模型的最优组合模型，如ARIMA 与非线性自回归神经网络模型组合，加强赤潮相关影响因子的收集并纳入时间序列模型中。这样既保留模型本身的线性预测能力，又弥补了其在非线性预测方面的不足，以期提高模型预测精度。

（4）本文所建立的ARIMA 模型具有简捷经济实用、业务性强的特点。但同时值得注意的是，因其仅考虑时间序列上的依存性和随机波动的干扰性，对于超历史极值会有无数据依存导致拟合不佳的情况。如2004 年5 月出现历史第一极值“59 次”，分析其原因主要是海水养殖面积、沿海城市集聚发展导致近岸海域4类及劣4类海水比例在2004年达到峰值，同期海温也处于快速上升期。在营养盐充沛供给、水文气象条件适宜等多种因素共同作用下导致了赤潮频繁爆发，出现超历史极值。因此，下一步研究中需将时间序列模型的预测结果与其他关联因素相结合开展综合统计分析，进一步改进超历史极值情况的预测精度。