局地误差子空间变换卡尔曼滤波方法的最优参数选取

王昊运，王辉，张宇，万莉颖

（1. 国家海洋环境预报中心，北京100081；2. 中国海洋大学海洋环境与生态教育部重点实验室，山东青岛266100；3. 国家海洋局海洋灾害预报技术研究重点实验室，北京100081）

1 引言

在大气和海洋模式中，初始状态对于数值模拟的效果至关重要。作为一种顺序同化方法，集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）及其演变的集合同化方法，集诸多优点于一身，是现有同化方法中最具应用发展前景的一个[1-3]。EnKF 通过将多个扰动的初始样本作为一个集合[4]，利用这个集合估计背景误差协方差，对卡尔曼滤波方法进行了有效简化。EnKF 的优势还在于：其计算代价比卡尔曼滤波和扩展卡尔曼滤波小得多；不要求背景误差协方差是线性演变的；不要求发展模式的线性和伴随模式；可以给集合预报提供好的初始扰动[4-5]。

为了解决EnKF 在大气和海洋数值模拟的应用问题，最重要的两个改进就是背景误差协方差的膨胀和局地化分析[6]。通常，模式的状态向量维数很高（为107），远远大于集合样本的维数，这会导致背景误差协方差矩阵中的虚假相关。同时因为集合样本离散度的问题，也会导致同化分析对背景误差协方差的低估[7-8]。EnKF及其演变而来的局地化分析在大气和海洋数值模拟中得到了广泛的应用[9-12]。

集合同化的优势在于：集合同化方法不仅给出模式状态的最优估计，而且不需要建立预报模式的切线性和伴随，背景误差协方差“流依赖”。在En-KF同化方法获得成功的基础上，为了不对观测进行扰动，发展了一系列演变、改进的同化方法。例如：集合调整卡尔曼滤波（Ensemble Adjustment Kalman Filter，EAKF）、集合变换卡尔曼滤波（Ensemble Transform Kalman Filter，ETKF）、奇异演变插值卡尔曼滤波（Singular Evolutive Interpolated Kalman Filter，SEIK）、集合平方根滤波（Ensemble Square Root Filter，EnSRF）等。由于顺序同化公式简明、应用相对容易，EnKF 及其演变版本得到了快速的发展和应用[13-14]。观测上不加扰动进行同化，能够解决EnKF 计算量大和集合成员少时收敛速度慢的问题，这一系列方法被统称为集合均方根滤波[15-17]。例如比EnKF 更加高效的SEIK 方法，由于采用了二阶取样法，因此可以用更少的集合样本数达到比EnKF 更好的效果，同时避免了EnKF 对观测向量扰动带来的人为误差，所以更加节省计算资源并且更加有效。实际应用中决定集合同化方法计算代价最关键的就是集合样本数，它直接决定了该同化方法需要在预报步时积分模式的次数。Nerger等[18]结合了ETKF在低维集合样本展开的子空间对误差协方差矩阵估计的优势和SEIK 采用二阶取样法可以带来的小样本数的优势，提出了误差子空间变换卡尔曼滤波（Error Subspace Transform Kalman Filter，ESTKF）。ESTKF 被证明是一种更加高效的误差子空间滤波，其局地化分析方案称为局地误差子空间变换卡尔曼滤波（Local Error Subspace Transform Kalman Filter，LESTKF）[19]。

LESTKF 在实际应用中，同样需要解决背景误差协方差矩阵的低估和因为计算能力不足导致集合样本数过小引起的虚假相关。因此局地化方案中的重要参数“局地化半径”和LESTKF分析方案中用来膨胀背景误差协方差矩阵的“ 遗忘因子”（Forgetting Factor）这两个重要参数对同化效果起着决定性的作用[19]。研究这两个参数如何影响LESTKF 的同化性能和同化效果，以及如何选取这两个参数才能最小化分析误差，对于将该同化方法应用于实际的大气海洋模式是十分关键的[20]。本文利用Lorenz96 模型结合LESTKF 同化方法，通过“局地化半径”和“遗忘因子”设置孪生实验，研究这两个重要参数对于同化效果的影响。

本文将首先探究“遗忘因子”对背景误差协方差膨胀效果及同化结果的影响；其次将研究“局地化半径”和“ 遗忘因子”的共同影响；最后结合Lorenz96 模型孪生实验的结果分析这两个重要参数在集合同化分析中扮演的角色，并针对如何优化选取参数提出建议和总结。

2 同化方法及同化框架

2.1 ESTKF同化方法介绍

对于非线性海洋大气系统而言，海洋大气在tk时刻的n 维状态向量为xk，和它对应的误差协方差矩阵为PK。m 个集合成员组成的状态向量集合可表示为x(α)k,α = 1,…,m。用集合均值来表示对tk时刻的状态估计：

同化预报时首先将集合样本分别通过模式积分至同化时刻。

在ESTKF分析步中，背景误差协方差Pf在形式上用集合样本Xf表示，即：

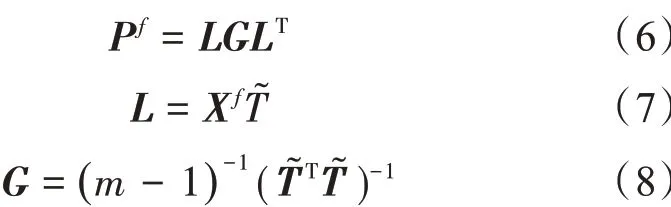
式（7）和（8）中：T͂是一个m ×( m - 1)维的满秩矩阵，并且每列元素的和为零，即

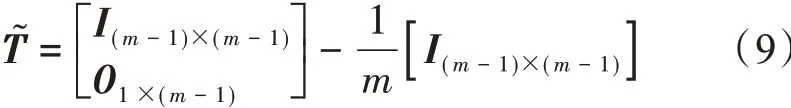
T͂矩阵的作用是在计算矩阵L 时剔除集合样本矩阵Xf的集合平均，即计算集合扰动。值得注意的是，矩阵L 是个n ×( m - 1)维矩阵，只存储前m - 1个集合扰动。

分析场通过集合扰动矩阵L给出：

式（10）——（12）中：权重向量wˉ、变换矩阵A͂分别为（m-1）维、（m-1）×（m-1）维。参数取值范围为0＜ρ͂≤1，称作“遗忘因子”，用来放大背景误差协方差。ρ͂作为该同化方法的重要参数，其取值直接影响着ESTKF的同化效果，也是本文中的主要研究对象之一。

该方法在得到分析场后需要进行再取样。由于集合样本矩阵经过了变换用X͂a表示，P͂a同理。

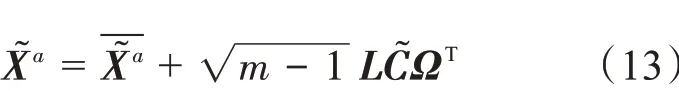
根据之前的研究，在SEIK 中，矩阵C͂-1由A͂-1经过Cholesky 分解得到，即( C͂-1)TC͂-1= A͂-1。Ω 是一个m ×( m - 1) 维的矩阵，该矩阵所有列向量相互正交，并且与(1,…,1)T也正交。矩阵Ω 的作用是与( m - 1)×( m - 1) 维 的 集 合 变 换 矩 阵A͂-1重 新 生成新的集合扰动矩阵。在ESTKF 中，Ω 矩阵记为Ω̂，即：

式中：Ω̂为Householder 矩阵[18]。Ω̂的作用为将Xf（n×m 维）集合样本空间中的向量投影在矩阵L（m-1个集合扰动）所在的误差子空间。同样矩阵Ω̂是满秩矩阵，并且列向量和为零。将式（8）——（13）中的T͂矩阵替换为Ω̂矩阵，最终算法就是ESTKF。

除了传统的EnKF 等滤波的优势之外，ESTKF的本质是在SEIK 的基础上将集合变换矩阵的计算通过Ω̂矩阵投影在误差子空间来完成。该方法相对于SEIK 来说：计算矩阵L 时，不必像之前一样忽略最后一列的集合样本，同时剔除了集合成员顺序的影响；ESTKF 由于在误差子空间计算，所以计算代价要小于SEIK。

2.2 局地化方案

为了消除集合样本数不足导致的背景误差协方差矩阵中的虚假相关，假设只有距离模式格点在一定范围（即局地化半径）内的观测才会对模式格点产生影响。局地化不仅可以减小虚假相关对同化效果的影响，还可以减小计算量，尤其当观测数量远远大于模式集合样本数时。而且局地化可以保证集合同化方法在高维模式应用上的合理性，即对于每个模式格点而言，模式状态的调整是在一个相对较大的集合空间内实现的。需要注意的是，由于局地化半径是为了消除虚假相关，而不同模式可能有不同的虚假相关，所以局地化半径随模式不同而不同。同时，局地化可能会在局地区域的边缘引起模式状态的不连续。为了解决这一问题，通常引入平滑的、以局地化半径为参数、以观测和格点距离为自变量的局地化函数，使得观测的影响随距离逐渐衰减。本研究中选用的局地化函数是五阶Gaspari-Cohn 相关函数[17]，即：

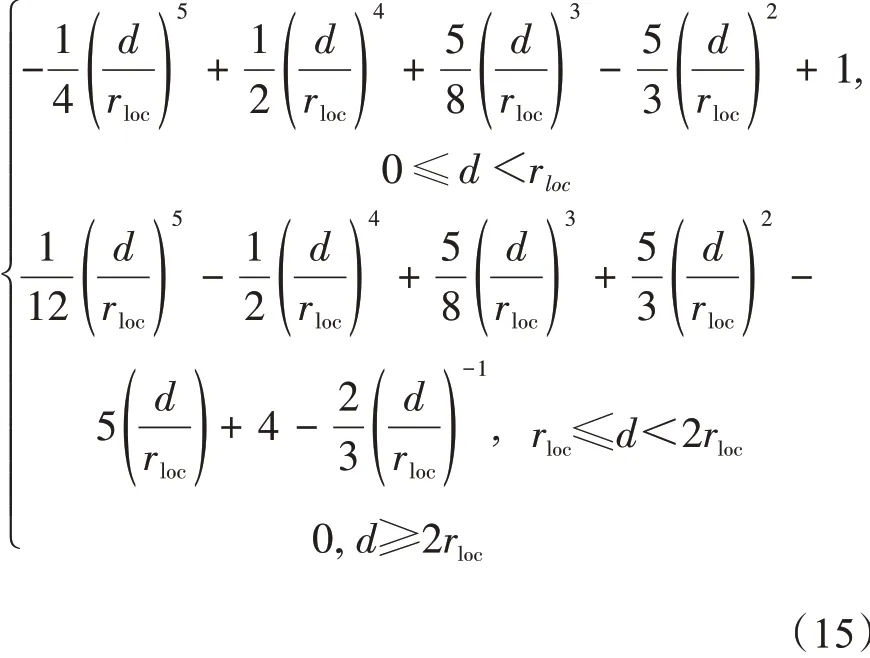
式中：d 表示观测到模式格点的距离，rloc表示局地化半径，计算结果表示观测对分析点的权重。利用Gaspari-Cohn 相关函数按照权重结合局地化半径中的观测得到该格点处的分析值。

参数ρ͂的选取对同化的影响主要发生在LESTKF 同化的分析步中，在协方差矩阵的计算中引入了一个膨胀因子来增加滤波稳定性。因为模式的强非线性，导致在相空间中对初值十分敏感，在同化中太过相信模式预报的背景场将容易导致滤波发散，因此该参数的选取对于同化效果有着重要的影响。

局地化半径通过把同化的区域分解成小的子区域，并行地同时更新每个格点的分析，更新时仅用到这个格点某一半径内的所有观测。在分析局地化的基础上，对该半径内的不同观测引入权重的局地化方法被称为观测局地化（Observation Localization，OL）。研究表明，在局地化分析时，针对不同的集合样本数局地化半径存在一个最优的选择[18]。

2.3 并行数据同化框架（Parallel Data Assimilation Framework，PDAF）

集合同化方法作为一种顺序同化方法，在海洋和大气领域得到广泛应用。EnKF、集合最优插值（Ensemble Optimal Interpolation，EnOI）提出后，为了解决计算代价等问题，集合平方根滤波等分析方法演变出一系列的集合同化方法，如ETKF、EAKF、减秩卡尔曼滤波（Singular Evolutive Extended Kalman Filter，SEEK）、SEIK、ESTKF 等。这些集合同化方法都是先由预报步分别积分集合样本；分析步仅需要模式提供的部分信息，通常只依赖于状态向量，而不是单个物理量场。例如在海洋模式的状态向量中，存储着U、V、z、S、T等模式变量场，或是需要估计的模式参数。对于观测算子H 的计算，只需要知道观测位置在状态向量中的存放位置即可。以上属性使得建立一个用通用方式实现集合同化方法的核心算法，并通过调用通用接口来进行同化的同化框架成为可能。这将极大地降低同化方案的实施。由于通用接口的设定，同化参数也便于系统化的管理和调整。

PDAF 同化框架就是一些集合同化方法的算法库（网址：http://pdaf.awi.de）[21]。目前全球大部分同化系统都是离线进行的，也就是模式集合积分与同化分析步分两个程序进行。这种同化方式虽稳定但低效。因为模式积分程序和同化程序之间需要用文件来传递信息，这种运行方式称为“离线模式”。另一种运行方式为直接将同化程序写进模式代码中整合成为一个程序，这种运行方式更高效，但是需要调整很小一部分模式代码，这种运行方式称为“在线模式”。前者是将模式积分和同化分析步分两个单独程序运行，模式的输出结果输入到同化程序，同化的分析场又作为模式的启动场；后者是将同化程序与模式耦合起来，需要对模式代码做扩展，调用PDAF 核心函数，形成一个完整的运行程序。 本研究中采用PDAF 同化 框 架结合Lorenz96 以“ 在线 模 式”运行。实际情况中由于模式复杂，往往采用“离线模式”[21-23]。

3 Lorenz96-PDAF孪生实验

3.1 实验设置及PDAF参数选取

Lorenz96 模型作为大气和海洋的低阶近似，具有非线性，存在混沌吸引子。Lorenz96 己经被广泛应用于大气海洋预测和资料同化的研究中[24]。其非线性强，同时对初值非常敏感，其动力框架为：

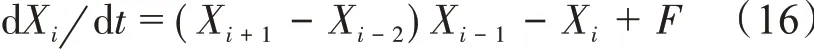
式中：Xi为模型变量,F为定常强迫，F的大小决定着非线性的程度。本文的实验设计中，模型维数等于dim_state=40，即i = 1,2,…,40，强迫项F 选为8，数值积分采用四阶龙格－库塔格式。

对于孪生实验而言，将模式积分10 000 步得到的状态向量的时间序列作为“真值”，并用第1 001步时的模式状态作为初始场（前1 000 步为模式调整阶段，即“spin up”阶段），其状态向量序列即为40×10 000维的矩阵。

观测序列是在Lorenz96 模式“真值”序列的基础上，加上不相关的随机噪声生成的。本节中，为了探索不同同化强度下遗忘因子和局地化半径的影响，扰动了不同的观测序列，两个观测序列的标准差分别取为1.0和0.1。为了去除模式调整阶段的影响，本实验只同化1 000 步之后的观测，采用积分一步同化一步观测的方式。

用于集合同化的初始集合样本由二阶取样法（Second-order Exact Sampling）在10 000 步模式“历史真值”的基础上生成初始样本。本节为了探究遗忘因子和局地化半径在不同样本数下的同化效果，分别用10个、30个样本做了对照试验。集合孪生同化实验流程见图1。

图1 集合孪生同化实验示意图

由于本孪生实验的Lorenz96模型和同化方法均在PDAF同化框架中进行，表1给出了主要同化参数的设置和选项。其中dim_ens 为集合样本数，forget和local_range分别对应“遗忘因子”和“局地化半径”。

表1 同化实验主要参数

3.2 遗忘因子对同化效果的影响

为了探究不同遗忘因子对同化结果的影响，本实验采用local_range为5个模式格点、rms_obs=1.0、dim_ens=30；但将遗忘因子取不同值。将同化结果、模式预报结果与模式真值、估计值（30 个样本的集合平均）做均方根误差（Root Mean Square Error，RMSE）对比，综合探究遗忘因子对同化结果的影响。为了方便表述，以下遗忘因子均记为f值。

图2 给出了同化至1 000 步，即模式第2 000 步的真值、观测值、估计值和分析场。图2a 和2b 分别为第2 000 步的真值和观测值；图2c 和2d 分别为f =1.0 时模式估计场和同化分析场；图2e和2f分别为f =0.9时的模式估计场和同化分析场。

通过对比发现模式第40 个格点上的观测值相对真值出现了较大扰动（见图2b、2d、2f 的红框部分）。而只有f= 0.9的分析场有一个抬升，向观测值做出了调整，这正是因为f 对背景误差协方差的膨胀作用导致的分析结果向观测偏移。

为了研究f 对分析场和预报场的影响，本实验又将f 的取值扩大为0.5～1.0，并计算其同化5 000步后与真值的RMSE。

图3 分别为预报场和分析场的RMSE，横坐标为同化步（因为时间步过于密集，因此每隔50 步填值，横坐标100 即代表第5 000 步，以此类推）。f 从上到下由0.5（协方差膨胀最大）递增至1.0（协方差不膨胀）。

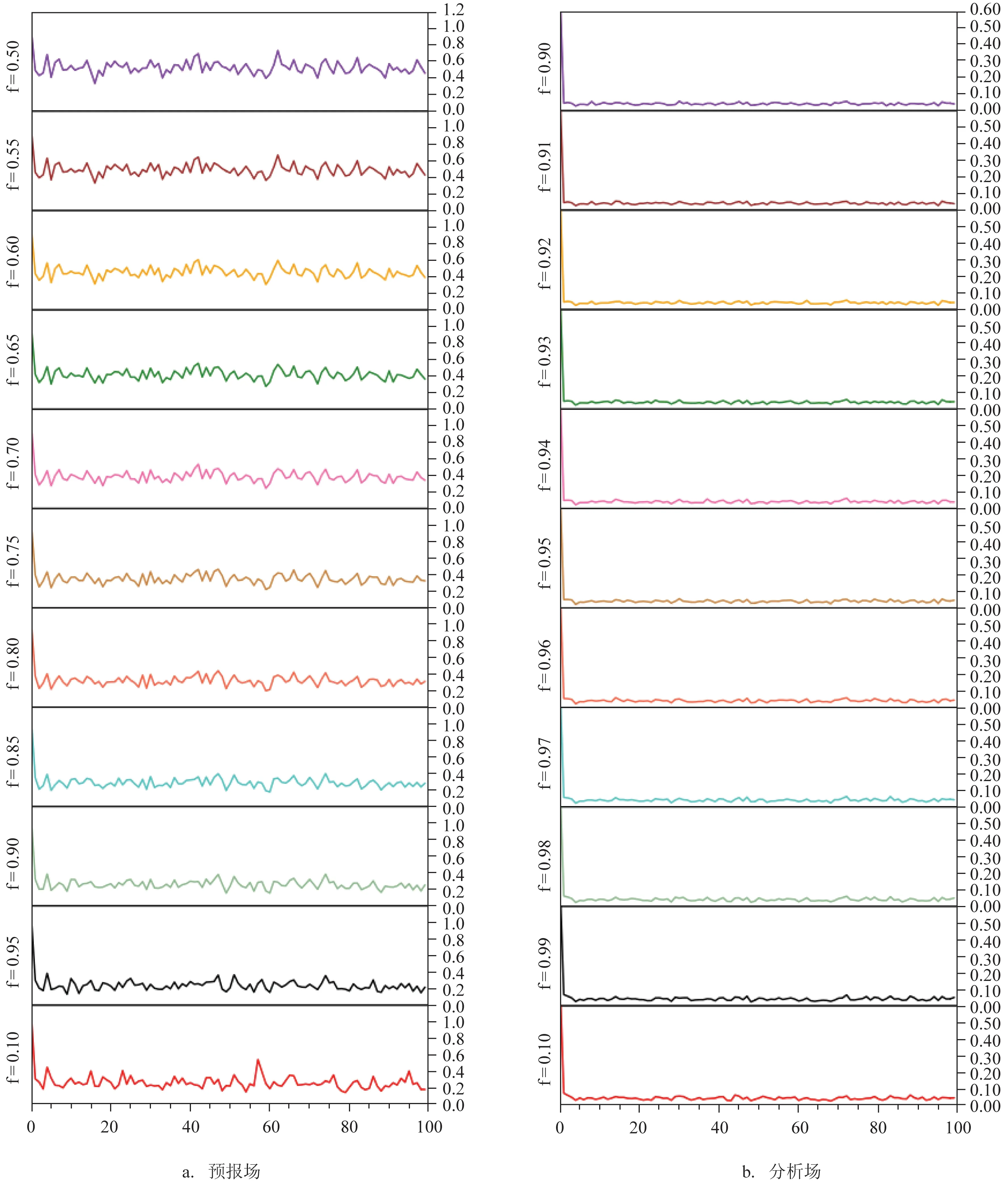
图3 预报场和分析场RMSE（横坐标为缩放50倍的时间步，纵坐标为与真值的RMSE）

对于单个RMSE 序列来说，在同化开始时RMSE 最大。这是因为初始样本是从模式之前的“历史状态”中提取的，与真值的误差最大；但随着同化预报步和分析步的交替，预报场和分析场均迅速向真值收敛。但是随着同化实验的进行会出现误差的突然增长。该特征与Pham[8]的图1一致。这一现象可能由于Lorenz 系统进入了强的非线性区域所导致。

通过图3a、b 的对比，发现LESTKF 对于所有实验而言均对预报场有所改善，但不同f 值的改善程度不同。通过纵向比较可以看出：f为0.95与f为1.0时，f 的使用明显避免了同化至3 000 步左右（图中横坐标约60）的误差爆发；f 为0.5 时误差最大；从上到下RMSE有一个先减小再增大的过程。

为了探究遗忘因子整体对同化结果的影响，分别对5 000 步同化实验的预报场和分析场的RMSE求时间平均（见图4）。结果表明：f =0.95 时分析场和预报场的误差最小；随着f 的减小，误差随之增大。f =1.0 时分析误差和背景误差均存在着低估，随着f 减小低估得到改善；但随着f 继续减小，则出现了分析误差和背景误差的高估，导致同化结果过于接近观测从而偏离真值。蓝线和黑线的交点则是最优f 值。这说明遗忘因子通过控制对背景误差协方差的估计会显著影响同化效果，高估和低估均不是最优f值。

图4a、b 的对比表明对于固定的f 而言，分析场相对于真值的RMSE 明显小于预报场相对于真值的RMSE。例如当f =0.95 时，预报场相对于真值的RMSE 约为0.25，而分析场相对于真值的RMSE 约为0.2。这说明f 通过对背景误差协方差的放大的确可以改善LESTKF 的同化效果；但随着f 越来越小，分析场对于预报场的提升依然存在，但提升效果开始变小。

3.3 局地化半径与遗忘因子的共同影响

本实验根据Nerger 等[18]的实验设置，将total_steps 设置为60 000 步，得到的结果作为真值；观测依然在真值的基础上增加随机扰动，观测误差分别以1.0 和0.1 的标准差生成。前1 000 步仍然作为“spin up”阶段。本实验将通过不同的观测误差控制同化实验的强度。集合样本分别取10 个和30个。因为在实际的集合同化实验中，往往因为计算资源的限制，不会选取过多的集合样本，因此选取10个集合样本更加接近实际情况。

local_range 的范围为0～20 个格点，这是因为：Lorenz96 模式共有40 个格点，并且是周期边界条件；local_range 超过20 个格点后相当于没有局地化分析。将不同f 和local_range 组合进行同化实验，结果依然用RMSE 的时间平均来表示。当时间平均RMSE 大于设定的观测误差时，认为发生了滤波发散。

图5a 给出了30 个集合样本、观测误差为1.0 的组合实验结果；5b为10个集合样本、观测误差为1.0的组合实验结果；5c为10个集合样本但观测误差降低至0.1 的组合实验结果。格点上的数字代表二者组合实验分析场的时间平均RMSE，白色格点说明该参数组合实验结果的误差超过了设定的扰动的观测误差，发生了滤波发散，因此不填色。

图5 可以看出当集合样本数为30 个时，不论local_range 和f 如何选取，均没有发生滤波发散，而且存在一个最优的参数组合区域。这表明当集合样本数足够大、同化方法对背景误差协方差的估计很精确时，引入遗忘因子和局地化分析依然对提高同化结果有帮助，能够找到一个最优的参数搭配区域。例如图5a中local_range＞6、f ＞0.93的区域。

当集合样本数为10个时，这种情形更加接近实际同化，如图5b、c 中出现了大面积的滤波发散区域。值得注意的是，最优的参数选择区域和滤波发散区域非常接近，两者紧邻。例如local_range = 7、f = 0.98 时，RMSE 约为0.2；但是当local_rangen = 8、f仍然为0.98时，则出现了RMSE为3.5的滤波发散，这个结果与Nerger等[18]的结果仍然一致。Nerger解释是由初始样本随机选取引起的同化实验前期的过渡阶段导致的，差的随机初始样本会使该过渡阶段变长，因此导致滤波发散。

图4 时间平均RMSE（蓝线代表与真值的误差，黑线代表与估计真值的误差）

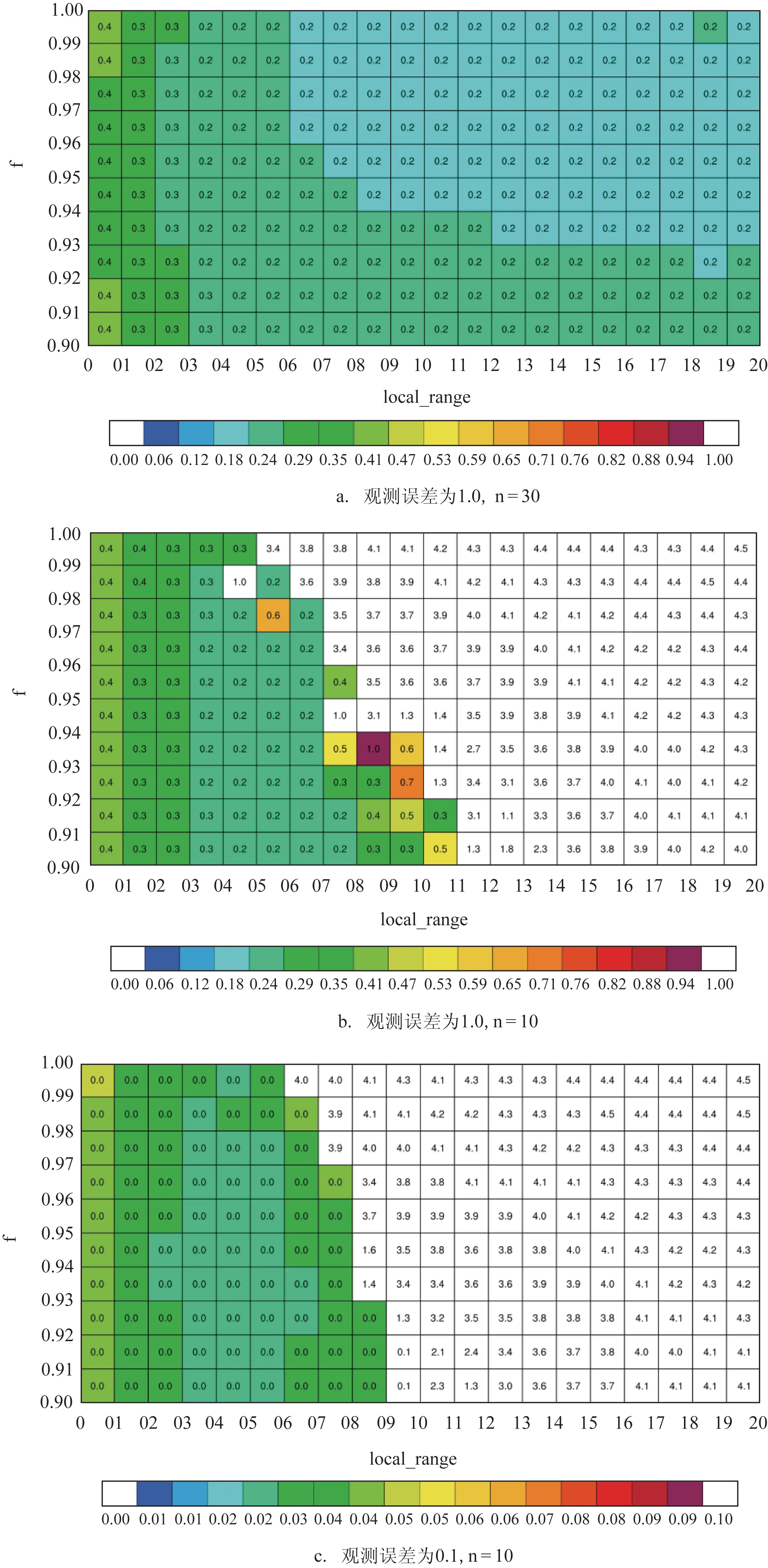
图5 组合实验结果（表中数字代表RMSE，白色区域为滤波发散区）

为了探讨观测误差对于同化实验的影响，将观测重新用0.1 的标准差随机生成，并同样用10 个集合样本做了组合实验，结果见图5c。当通过减小观测误差来增加同化强度时，滤波发散的区域有所增大，但依然存在一个最优的参数选择区域。

4 总结与讨论

本文通过Lorenz96 模型的孪生实验，分别验证了局地化半径和遗忘因子的不同选取对同化分析场的影响，并且详细介绍了PDAF 同化中一些参数的设置。结论如下：

（1）局地化半径对分析结果的空间分布影响明显：局地化半径过大，不能很好地滤去背景误差协方差矩阵中的虚假相关；局地化半径过小则分析太细节化，使得物理量场不符合实际。

（2）遗忘因子作为单独影响同化实验的因子时，分析误差随着f 值的增大有一个先减小再增大的过程。这是因为f 值控制着对分析误差协方差和背景误差协方差的估计，对真值的低估和高估均会引起误差。图4中可以清楚的看到，估计的RMSE与实际的RMSE 的交点就是理论上最优的遗忘因子。但在实际同化应用中，由于对真值的估计不准确，因此对于参数f的选取只能通过实验方法去寻找。

（3）f的选取对于同化效果影响显著。Lorenz96理想实验结果表明：f 的作用是人为放大背景误差协方差，防止滤波发散。f 取值并非越小越好，太小会使同化结果过于接近模式，从而减弱观测信息对模式的调整。f 恰当选取（取值为0～1），则可以明显提高同化效果。因此在实际同化中选取该参数时应格外注意。

（4）遗忘因子和局地化半径作为共同因子影响同化时，的确存在一个最优的区域。但是最优区域的选取需要慎重，因为最优的参数组合的区域往往在滤波发散的临界区域附近。一旦选取不当，则很容易出现滤波发散，这在实际同化中一定要注意。本文为今后进一步利用LESTKF实际同化业务应用中参数的最优化选取做了铺垫。

作为仍在不断发展的同化方案，ESTKF 及PDAF 同化框架已经得到越来越广泛的应用。由于PDAF 同化框架接口化、开源的特性，可以更方便地研究分析步中的其他参数并实现优化。例如，如何选取自适应的局地化半径（随纬度、同化的物理量而改变），以及如何进一步选取自适应的遗忘因子，以便协方差膨胀随着同化问题不同而变化，是值得进一步研究的问题。

资料同化是一个综合问题，不仅需要同化方案的演进，同时还需要计算技术的进步，二者缺一不可。怎样在不提高计算代价的前提下提高同化效果，是资料同化理论研究中的一个重要方向。是否能够提出一个更有效率的同化方案，并且能拥有集合滤波中随时间演变的背景误差协方差矩阵，仍是资料同化研究的一个重要问题。