基于IAHP和TOPSIS法的电能质量综合评估
2020-11-09磊胡文平王秋莎
王 磊胡文平王秋莎
(1.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2.中国电建集团河北省电力勘测设计研究院有限公司,河北 石家庄 050031)
0 引言
经济快速发展促使电力系统负荷结构日趋复杂化、多样化,众多新型电力负荷的投入(如光伏、风电)导致电网电能质量日益恶化,而新设备对电能质量又较为敏感,因此对电能质量的要求进一步加强。电能质量是用来描述客户从公用电网获取电能品质的高低、好坏。合理、准确、客观的电能质量综合评估,不仅为构建良好的电能质量市场[1]奠定基础,又为电力企业提高效率、降低成本提供技术保障。
目前,电能质量综合评估方法有很多[2-8]。文献[2]提出了基于模糊原理的综合指标和电能质量评估的模糊模型,在指定隶属度样本集合的条件下实现电能质量的综合评估。文献[3]提出了一种模糊综合评判的二级评判法,事先给定主观权重,然后进行电能质量综合评估。文献[4]采用组合赋权的评估方法有效克服了单一赋权法的缺点。文献[5]运用加权主成分分析进行电能质量评估。文献[6]运用遗传算法进行电能质量评估,2种方法使电能质量评估结果更加准确、具体。文献[7]采用模糊层次分析法、模糊数学综合评估供电服务质量,克服了主观判断的模糊不确定性难题。文献[8]应用模糊多目标决策理论的极大极大决策方法,相比其他方法,该评估方法更简单易行。
逼近理想解的技术(Technique for Order Preference by Similarity to deal Solution,TOP SIS),是一种非常有效的多指标决策模型,被广泛用于供应商选择、评估土地资源等领域,并取得了良好的效果。TOPSIS法在评估过程中涉及计算指标权重,使用层次分析法(analytic hierarchy process,AHP)可以求解多指标综合权重,该方法由专家分别比较各个指标的重要程度,从而得到判断矩阵,使用方便,原理简单,被众多技术人员使用[9-11]。但该方法存在弊端,当参与比较的指标数量较多时,构造出的判断矩阵经常难以符合一致性要求,而且由专家比较各指标的重要程度会引起评估结果带有主观色彩,限制了该方法的实用性和客观性。考虑层次分析法的此种缺陷,提出了改进层次分析法(IAHP),利用电能质量监测值得到初始判断矩阵推荐值,由IAHP 得到电能质量各指标权重[12-13],进而由TOPSIS法综合评估项目电能质量。
1 改进层次分析法(IHAP)
1.1 监测值计算初始判断矩阵
设指标体系中包含m项指标,分别为x1,x2,…,x m,监测点样本容量个数为n,x ij为第j个监测点的第i个指标值。由此可得原始数据矩阵
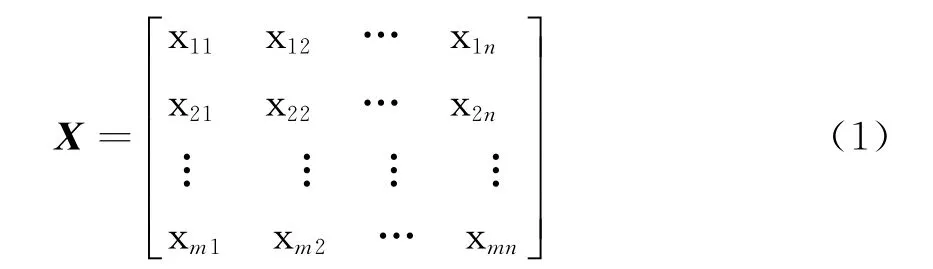
按照式(2)计算第j个监测点的第i个指标值x ij的严重度系数

式中:x ijlim为第i个电能质量指标合格等级所对应的数值[14]。
平均n个监测点的第i个指标的严重度系数

按照式(4)计算第i个指标的客观权重系数

按照式(5)计算两相邻指标客观权重系数比值

由式(5)计算结果并结合表1给出的对应关系,可得b i,i+1(1≤i≤m-1),由其形成初始判断矩阵B。
1.2 改进层次分析法求判断矩阵
层次分析法中检验一致性的根本是要求判断矩阵中元素的取值能够满足乘法传递性,然而这与其对元素取值的限制及其定义是矛盾的,因此采用加法传递性逼近乘法传递性[15]。
假设初始判断矩阵B中的元素每增加1,重要性程度增加Δ,作为基本重要性单元。通过初始判断矩阵B推导判断矩阵A的步骤如下:
a.当b i,i+1(i=1,2,…,m-1)>1时,a i,i+1=(b i,i+1-1)*Δ,说明b i比b i+1重要程度多a i,i+1。
b.当b i,i+1(i=1,2,…,m-1)=1时,a i,i+1=0,说明b i与b i+1同等重要。
c.当b i,i+1(i=1,2,…,m-1)<1时,a i,i+1=-(1/b i,i+1-1)*Δ,说明b i比b i+1重要程度多a i,i+1。
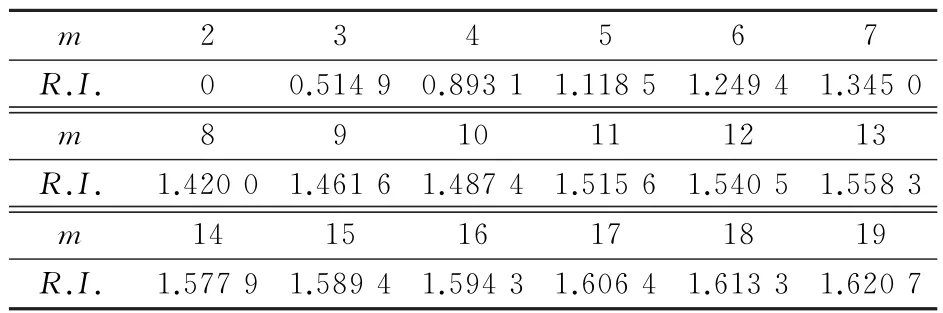
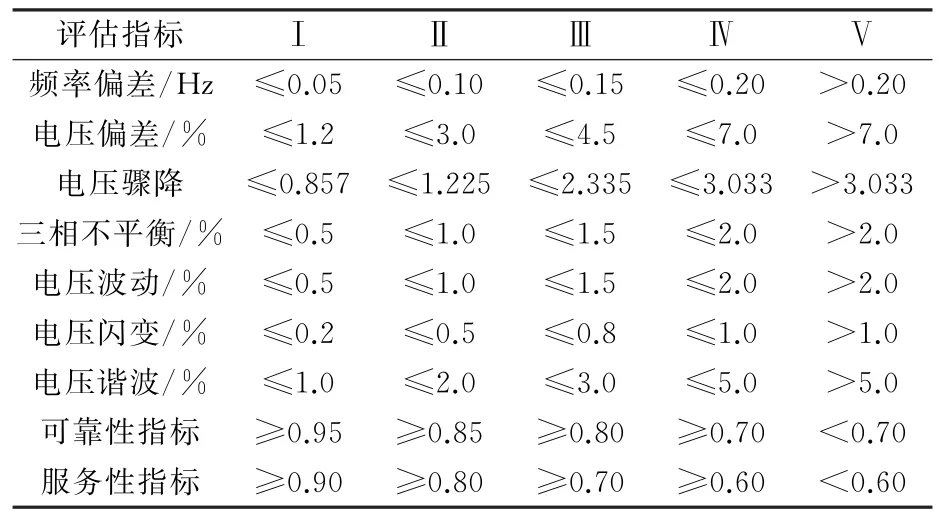
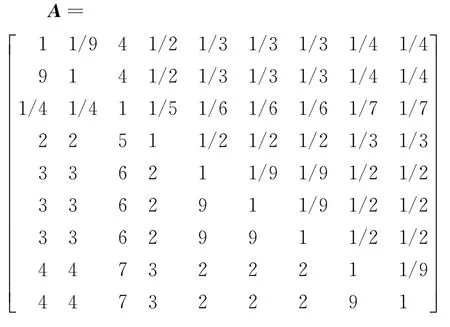
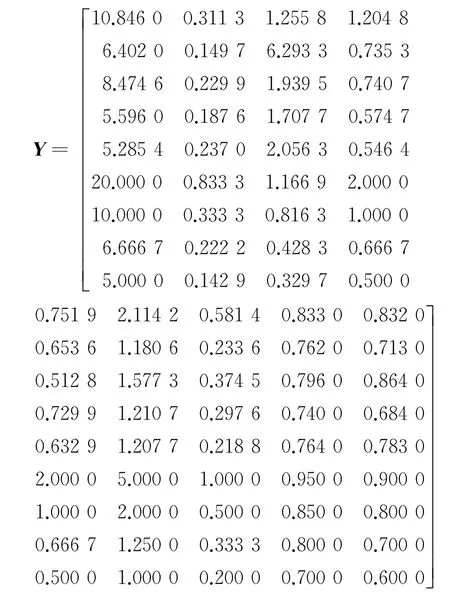
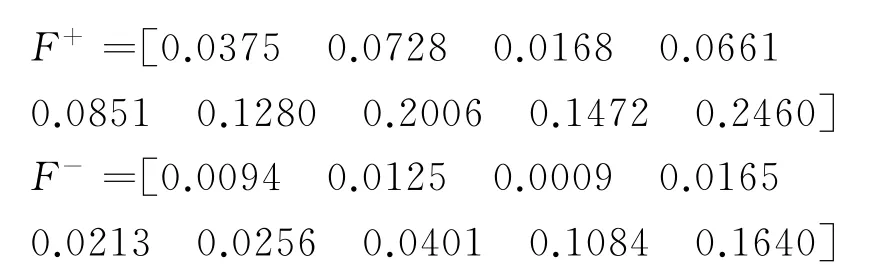
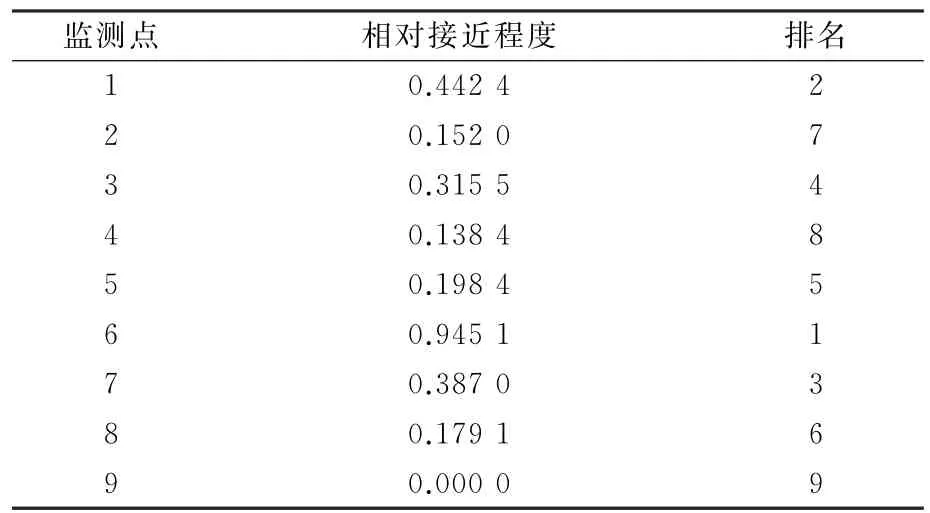
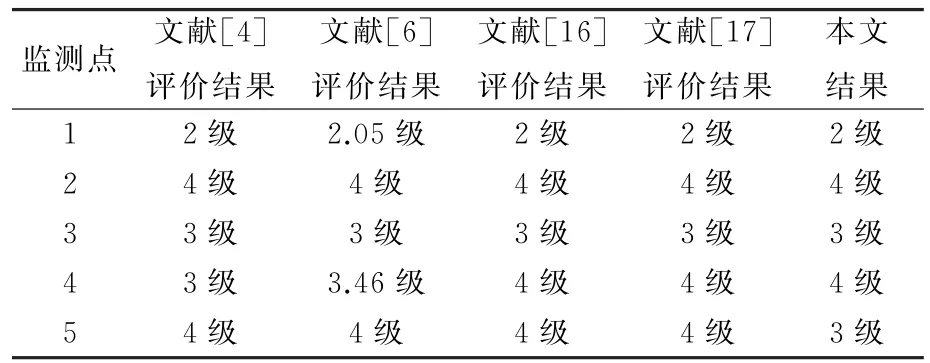
d.判断矩阵A的上半三角元素中除主对角线外其余元素的行坐标都小于其列坐标,用a ij(i 表1 a i,i+1取值原则 e.根据判断矩阵A为正互反阵这一性质,求出A的下半三角全部元素。 f.当通过上述法则求出的判断矩阵A中元素出现大于9或小于1/9时,按照层次分析法对判断矩阵元素的要求,分别强行赋值令其为9或1/9,可以得到最终判断矩阵A。 得到判断矩阵A后,再按照层次分析法的计算公式求电能质量指标权重,步骤如下。 a.按列对判断矩阵A=(a ij)m×m做归一化处理,可得矩阵Q=(q ij)m×m,其中, b.按行将矩阵Q相加得向量c =(c1,c2,c3,…,c m)T,其中, c.将c=(c1,c2,c3,…,c m)T归一化,可得最大特征值对应的特征向量,即权重系数 d.计算判断矩阵的最大特征值 e.计算衡量判断矩阵A不一致程度的一致性指标 f.用平均随机一致性指标R.I.(R.I.的取值与判断矩阵阶数的对应关系如表2所示)修正C.I.,可得随机一致性比率 表2 平均随机一致性指标 g.通过检验C.R.是否小于等于0.10进行一致性检验,所得数值越小,说明一致性程度越好,如大于0.10则无法通过一致性检验。 TOPSIS法开展电能质量综合评估步骤如下。 a.建立样本指标矩阵。 指标体系中包含m项指标,分别为x1,x2,…,x m,监测点样本容量为n,x ij为第j个监测点的第i个指标值,连同m项指标的p个等级限值一起构成样本指标初始矩阵。因为电能质量指标中含有效益性指标和成本性指标,故采取求倒数方法将成本性指标变成效益性指标。则初始矩阵变换后得到矩阵Y=(y ij)(n+p)×m。 b.建立加权化标准决策矩阵。 因各项指标量纲不同,且数量级大小相差也比较悬殊,每组比较数据存在不可比性,所以对上述矩阵进行标准化处理,可得矩阵E=(e ij)(n+p)×m,其中 构建规范化加权决策矩阵Z=(z ij)(n+p)×m,其中 c.确定规范化决策矩阵的理想解。 d.计算各评价点与理想解、虚拟最劣解距离。 各评价点与理想解的相对接近程度为 根据H+i的大小对各监测点和等级限值样本点进行排序,再根据其所处位置对各监测点进行分级,从而确定各监测点的电能质量等级。 采用文献[14]中的算例开展仿真分析,本地域5个监测点的电能质量实测数据如表3所示。 表3 监测点的实测数据 依据我国公认要求,将电能质量各指标划分为5个等级,从Ⅰ-Ⅴ分别对应优质、良好、中等、合格与不合格,指标等级界限值如表4所示。 表4 指标等级界限值 电能质量各项指标中,除可靠性、服务性指标外,其他指标均是越小越好,为了保证数据的一致性,考虑可靠性和服务性指标满分为1的原则,将可靠性和服务性指标作如下处理:1-可靠性、1-服务性。通过计算可得初始判断矩阵 可得判断矩阵 可得电能质量指标权重 运用TOPSIS法综合评估电能质量,可得样本指标矩阵 构建规范化加权决策矩阵 确定规范化决策矩阵的理想解F+、F- 各监测点到理想解距离D+、到负理想解距离D-、与理想解的相对接近程度H+为 电能质量综合评估结果如表5所示,表5中监测点6—9 评估结果表示等级Ⅰ—Ⅳ的评估结果,因此可得监测点1—5 电能质量综合评估结果,其等级分别为2级、4级、3级、4级、4级。评估结果与文献[4],[6],[16],[17]评估结果对比,如表6所示。 表5 综合评估结果 表6 评估结果比较 除监测点5外,评估结果与其他文献评估结果基本一致,其他文献计算权重方法均包含主观因素,文中评估方法无论是计算权重还是综合评估均以监测数据为基础,结果具有客观性。此外,该方法除了可以评估监测点电能质量等级外,还可以比较监测点电能质量好坏,即使同一等级的监测点,通过表5也可以确定其优劣。 以上提出的电能质量综合评估模型通过电能质量监测值得到初始判断矩阵推荐值,再由IAHP计算各指标权重,应用TOPSIS 法进行电能质量综合评估,该模型以监测数据为基础能够保证评估结果的客观性,尽可能的减少了人为主观因素的影响,提供了一种电能质量综合评估的新方法。同时,该方法既可以得出各个监测点电能质量等级,又可以得出各个监测点电能质量优劣排序,因此提出的方法具有实用价值。
1.3 判断矩阵求权重
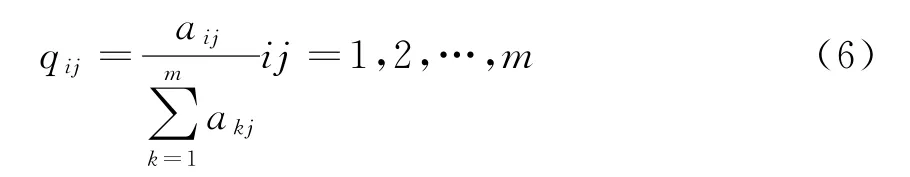
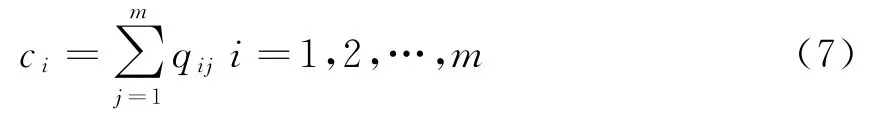
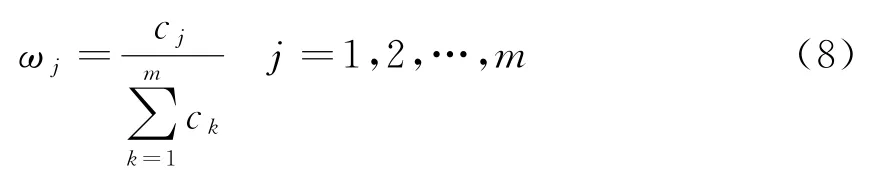
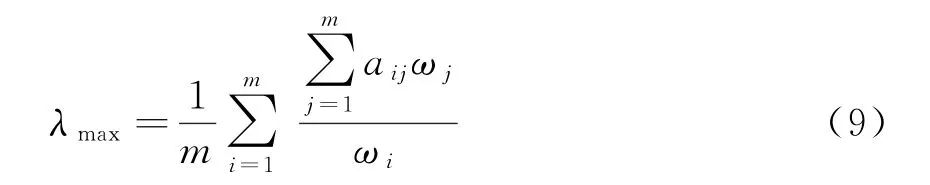


2 TOPSIS法数学模型

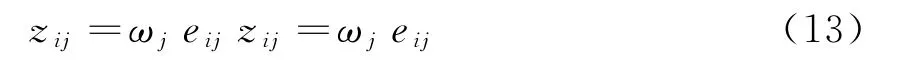

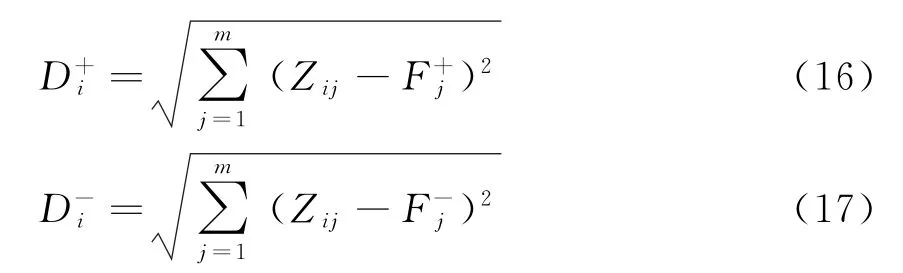
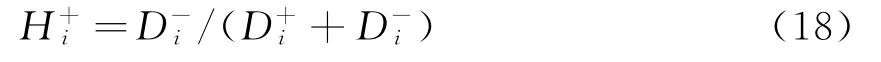
3 算例分析

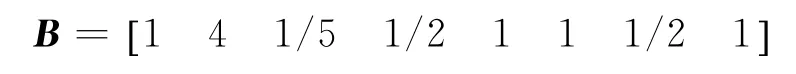



4 结论
