基于统一强度理论的巷道围岩松动圈计算方法
2020-11-09苏士龙高海海周康乐
苏士龙, 高海海, 周康乐
(1.华晋焦煤有限责任公司, 吕梁 033000; 2.山西华晋吉宁煤业有限责任公司, 临汾 042100)
巷道围岩松动圈是原岩应力及开挖、回采产生的采动应力作用于围岩体,导致其变形破裂的集中客观体现。松动圈发育厚度与支护难度密切相关,对巷道稳定性至关重要,是巷道支护设计的最为关键的参数之一。如何准确快速确定松动圈发育厚度一直是巷道围岩稳定性控制领域的热点和难点问题。目前松动圈发育厚度的确定方法主要包括现场测试法、数值分析法与理论计算法。现场测试法相对于其他方法更为准确,但存在现场工作量大,孤立测点代表性差等缺点。数值分析法能够批量模拟不同围岩条件和地应力条件下松动圈发育厚度,结果形象直观,但本构关系和边界条件的选取对计算结果影响较大,对于现场工程技术人员知识储备要求较高[1]。理论分析方法一直是地下工程领域分析围岩应力及破裂区分布常用的研究方法,工程现场技术人员以及设计人员可方便快速地获得参考性结论[2]。
中外学者对围岩松动圈理论计算开展了大量工作。王睿等[3]利用广义Hoek-Brown强度准则推导了理想状态下围岩松动圈厚度的计算公式。在铜旬高速某公路隧道中该方法计算所得围岩松动圈分布范围与围岩深部位移监测所得结果较为接近,验证了基于Hoek-Brown强度准则的围岩松动圈计算公式的准确性,为确定围岩松动圈半径提供了新的有效方法。余敏等[4]基于改进的双剪统一强度理论,得到了围岩松动圈半径的解析表达式。通过与已有方法计算结果的对比,验证了该方法的可行性,并进一步分析了中间主应力大小以及软化程度对结果的影响。李政林等[5]通过对围岩应力分布特点的分析,提出了基于损伤理论的围岩松动圈的界定标准,认为完全损伤区即为围岩松动破坏区。最后运用损伤理论解析解对张石高速公路隧道围岩松动圈进行了估算预测,同时将预测结果与现场监测值进行对比分析,验证了理论解的适用性。黄锋等[6]基于Drucker-Prager准则推导了围岩应力松动圈的弹塑性理论和损伤理论计算方法,其计算结果均小于单孔声波法测试结果,但两者变化规律类似。由于考虑了岩体的峰后软化特性,损伤理论分析法计算结果比弹塑性理论更加接近于实测值,运用损伤理论对围岩(特别是低级别围岩)松动圈进行预测是可行的,研究结果对其他类似工程具有借鉴作用。
目前广泛应用于围岩弹塑性分析的强度准则主要有Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论。既有研究结果主要是采用某一种强度准则对围岩松动圈厚度进行计算,缺乏同时采用两种或多种强度准则对松动圈厚度进行计算,并将计算结果与现场测试结果进行对比分析,以确定适用于松动圈理论计算的强度准则。
以吉宁煤矿2103工作面为工程背景,采用Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论分别对巷道围岩松动圈进行理论计算。将理论计算结果和现场测试进行对比,确定适用于围岩松动圈计算的强度准则。对巷道支护参数优化和围岩稳定性研究具有重要意义。
1 岩石的几种强度准则
岩石(体)的强度准则是进行围岩弹塑性分析的理论基础。过去的数十年,各国学者已经提出了各种各样的强度准则。目前广泛应用于围岩弹塑性分析的强度准则有Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论。
1.1 Mohr-Coulomb准则
1900年,德国著名科学家Mohr[7]提出了Mohr-Coulomb(M-C)准则,在岩石强度理论发展史中最为经典。由于M-C准则的数学表达式较为简洁、力学计算原理十分简单、计算结果偏于安全,故而在工程实践中得到广泛应用。其数学表达式为
(1)
式(1)中:σ1和σ3分别为最大主应力和最小主应力,MPa;c为岩石的黏聚力,MPa;φ为岩石的内摩擦角,(°)。
1.2 Hoek-Brown准则
Hoek等[8]于1980年提出了Hoek-Brown准则。后来Hoek等[9]于1992年提出了经改进的广义Hoek-Brown准则,其表达式为
(2)
式(2)中:σc为岩石单轴抗压强度,MPa;mb、s和α为表征岩体特征的经验参数。mb和s为常数,s取决于岩体的破碎程度,取值为0~1。
1.3 统一强度理论
统一强度理论表达式[10]为
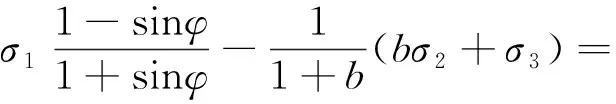
(3)
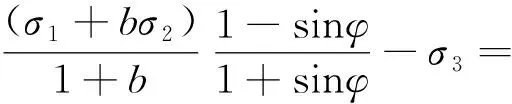
(4)
式中:F和F′为数学表达式;σ2为中间主应力,MPa;b为中间主应力影响系数,计算公式为
(5)
式(5)中:α为材料的拉压强度比;B为材料的拉剪强度比;σc、σt、τs分别为岩石的抗压强度、拉伸强度和剪切强度,MPa。
2 围岩松动圈厚度弹塑性分析
巷道围岩弹塑性分析的基本假设如下。
(1)断面形式为圆形。
(2)围岩为连续、均质、各向同性体。
(3)初始地应力为自重应力,且为各向等压状态即侧压系数λ=1。
受限于篇幅,同时已有学者对基于Mohr-Coulomb准则和Hoek-Brown准则的松动圈计算公式进行推导,在此不再赘述。仅推导基于统一强度理论的松动圈计算公式。
2.1 围岩的塑性区应力
假定巷道半径为r0,受到地应力为P0,支护阻力为Pi,塑性区半径为Rp,松动圈半径为R0。受到切向应力为σθ。计算简图如图1所示。
在平面应变问题中,中间主应力可假设为
(6)
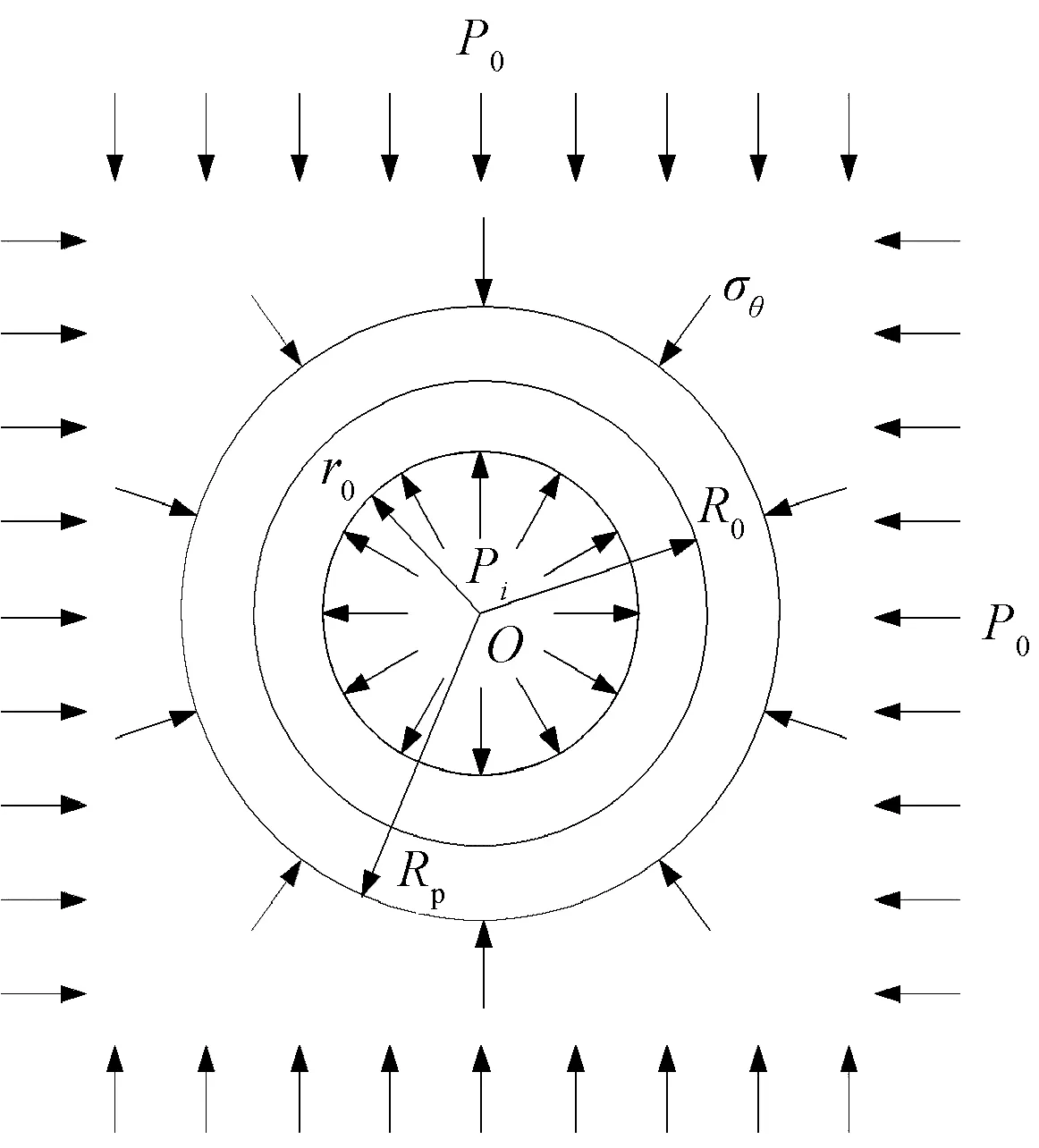
图1 力学分析模型Fig.1 Mechanical analysis model
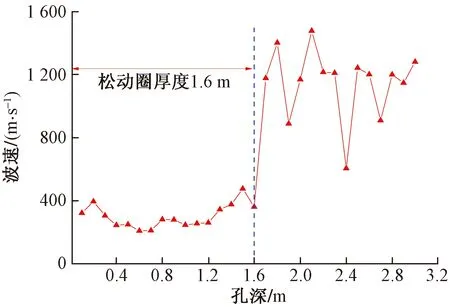
式(6)中:m为中间主应力系数,0 将统一强度理论表示为极坐标系: (7) (8) 式中:σr为径向应力,MPa;σθ为切向应力,MPa。 将式(6)代入式(7)中,可得: (9) 则式(9)改为 (10) 不计体力时,平衡微分方程为 (11) 在轴对称应力状态下,弹性区的应力可以通过应力边界条件和位移单值条件求得 (12) 式(12)中:σre为弹性区径向应力,MPa;σθe为弹性区切向应力,MPa;σR为弹塑性分界处的径向应力,MPa。 整理式(10)可得 (13) 式(13)中:σrp为塑性区区径向应力,MPa;σθp为塑性区切向应力,MPa。 将式(13)代入式(11),可得 (14) 式(14)中:C0为积分常数。 根据边界条件可以求得 (15) 将式(15)代入式(14)中,可得 (16) 将式(16)代入式(13),可得 (17) 松动圈的定义如下:松动区边界上,围岩的切向应力等于初始地应力,即σθ=P0。因此可得 (18) 通过式(18)可以求解松动圈半径R0。 基于Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论松动圈,计算公式如表1所示。 通过表1中表达式即可求得不同强度准则条件下围岩松动圈厚度理论计算值。 表1 不同强度准则计算松动圈厚度表达式Table 1 Different strength criteria to calculate the thickness of the loose circle 吉宁煤矿所处井田位于华北板块鄂尔多斯地块河东区块的南部边缘,河东区块东部以离石断裂为界,西部为黄河,南部和北部是沉积带边缘。井田总体为一向西倾斜的单斜构造,以褶曲为主,次级褶曲走向主要为南北向,较少断裂,未见大规模的岩浆活动。地层由老到新,自东南向西北出露有二叠系上石盒子组下段、中段、上段及石千峰组地层。2103工作面所处煤层松软、节理裂隙发育。巷道断面为矩形,掘进断面宽×高(W×H)为4 400 mm×3 700 mm。顶板和两帮采用Φ20 mm×2 400 mm的锚杆支护,锚杆间距为800 mm。 选取距2103工作面轨道顺槽1 050 m断面帮部进行围岩松动圈理论计算和现场测试。该断面埋深h约为515 m,巷道围岩为煤岩,重度γ=23.90 kN/m3。初始地应力P0为12.31 MPa。支护阻力Pi为0.1 MPa。 3.2.1 Mohr-Coulomb准则 根据室内试验结果可知:煤岩黏聚力c=14.10 MPa,内摩擦角φ=22.90 °。将确定好的物理力学参数代入表1中计算公式可得松动圈厚度为2.30 m。 3.2.2 Hoek-Brown准则 根据室内试验结果,同时查阅相关规范,通过计算可得:σc=22.93 MPa,mb=6.28,s=0.020 9,α=0.500 201。代入表1中计算公式可得松动圈厚度为0.77 m。 3.2.3 统一强度理论 根据室内试验结果可知:煤岩黏聚力c=14.10 MPa,内摩擦角φ=22.90 °。将室内试验结果代入式(5)可得:中间主应力影响系数b=0.49。将物理力学参数代入式(18)求得松动圈厚度为1.48 m。 对2103工作面选取的典型断面进行围岩松动圈现场测试。由于单孔超声波测试法具有仪器操作简单、经济适用的优点[13],本次测试采用单孔超声波测试方法,测试设备选用BA-II型超声波围岩裂隙探测仪。超声波测试法确定松动圈厚度的原理为:利用超声波检测仪,依据超声波在完整性不同的岩石中传播速度不同的特性,通过测量与分析参数,推断松动圈范围。 现场测试工作过程如下。 (1)钻孔扫眼,清出眼孔中的岩粉和碎石渣,钻孔直径60 mm,孔深3 m,向下倾角5°。 (2)将探头送至孔底,封孔器插入孔口并固定好(向下打钻孔不用封孔器)。 (3)注水,测杆尾端连续有水流出时,表明水已注满。 (4)测试读数,将探头向外逐次抽动10 cm,每次读数计时。 (5)测试时,在钻孔每个深度位置,旋转不同角度,测试三组数据,取其平均值。 现场测试主要步骤如图2所示。 将现场测得数据代入波速计算公式转换成波速,并对异常数据剔除或修正,对钻孔测点波速数据进行分析,绘制孔深-波速曲线图,得到2103工作面典型断面测孔不同深度处波速变化情况,如图3所示。 图2 松动圈现场测试过程Fig.2 Field test process of loose circle 图3 2103工作面孔深-波速曲线图Fig.3 Hole depth-wave velocity curve of 2103 working face 从图3曲线可以看出,波速随测孔深度增加基本呈逐渐增大的趋势,且在某一点波速会出现较大波动,因此可将此点作为围岩松动区与完整区的分界,即此点对应深度为松动圈厚度。观测结果显示,松动圈厚度约为1.6 m。 通过与现场测试结果进行对比可知以下结果。 (1)Mohr-Coulomb准则计算松动圈厚度值大于现场测试结果,相差0.7 m。因此采用Mohr-Coulomb准则计算松动圈厚度结果比较保守。 (2)Hoek-Brown准则计算松动圈厚度值小于现场测试结果,相差0.83 m。因此采用Hoek-Brown准则计算松动圈厚度结果安全性值得考虑。 (3)统一强度理论计算松动圈厚度值与现场测试结果比较接近,仅相差0.12 m。 综上可知:统一强度理论计算结果与现场测试结果更加接近,适用于巷道围岩松动圈计算。 (1)基于弹塑性理论,采用统一强度理论推导获得了围岩松动圈厚度计算公式。分别采用Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论对吉宁煤矿2103工作面典型断面围岩松动圈进行计算。三种方法理论计算结果分别为2.30、0.77、1.48 m。 (2)采用单孔超声波测试法对吉宁煤矿2103工作面典型断面巷道围岩松动圈进行现场测试。现场观测结果显示,松动圈厚度为1.6 m。将Mohr-Coulomb准则、Hoek-Brown准则和统一强度理论3种方法理论计算结果和现场测试结果进行对比,表明基于统一强度理论计算松动圈厚度与实测结果比较接近,适用于围岩松动圈计算。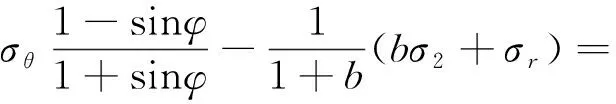
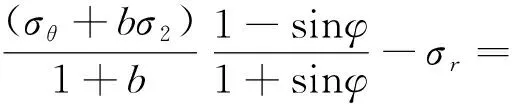
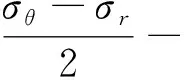
2.2 围岩的弹性区应力
2.3 围岩松动圈分析
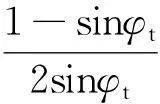
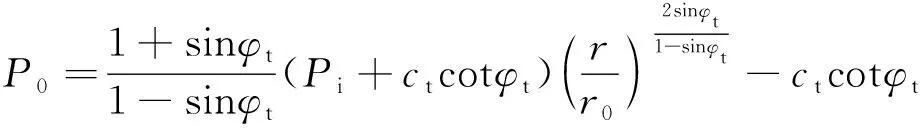

3 工程算例分析
3.1 工程概况
3.2 围岩松动圈理论计算
3.3 围岩松动圈现场测试

3.4 对比分析
4 结论