水运工程受弯构件的混凝土裂缝宽度计算建议

李晓慧，仝成才

(中交天津港湾工程设计院有限公司大连分公司，辽宁 大连 116001)

《水运工程混凝土结构设计规范》[1]推荐采用HRB400级、HRB500级钢筋，《钢筋混凝土用钢第2部分：热轧带肋钢筋》[2]及《公路钢筋混凝土及预应力混凝土桥涵设计规范》[3]均已取消了335 MPa级钢筋。因此，淘汰低强钢筋，推荐高强、高性能钢筋是未来发展的趋势。采用高强钢筋后，混凝土构件在使用状态下的钢筋应力将提高、裂缝宽度将增大、刚度将减小，这样就可能造成钢筋的配置不是由承载力控制，而是由裂缝宽度和刚度要求来控制，从而使高强钢筋的强度得不到充分利用，限制了其强度的发挥，不利于高强钢筋的推广。本文通过对国内各专业混凝土结构规范的裂缝宽度公式进行对比分析，发现现行裂缝宽度计算公式不适用于高强钢筋，并提出规范公式的修改建议。

1 各规范裂缝宽度计算公式

1.1 水运规范

《水运工程混凝土结构设计规范》采用数理统计公式，裂缝宽度计算公式与旧版规范相同，是根据低强钢筋试验分析给出的[4]，裂缝宽度计算公式如下：

(1)

(2)

式中：Wmax为最大裂缝宽度；α1为构件受力特征系数；α2为考虑钢筋表面形状的影响系数；α3为考虑作用荷载影响的系数，准永久组合或重复荷载取1.5，对短暂状况的正常使用极限状态作用组合取1.0～1.2，对施工期可取1.0；σs为钢筋混凝土构件纵向受拉钢筋的应力；Es为钢筋弹性模量；c为最外排钢筋的保护层厚度；d为钢筋直径；ρte为钢筋的有效配筋率；As为受拉区纵向钢筋截面面积；Ate为有效受拉混凝土截面面积，轴心受拉构件取构件截面面积，受弯、偏心受拉、偏心受压构件取2αsb，其中αs为受拉钢筋重心至受拉区边缘的距离，b为受拉截面宽度。

1.2 建筑规范

《混凝土结构设计规范》[5]采用黏结滑移-无滑移综合理论，与旧版规范相比，本规范调整了计算时的荷载组合和受力特征系数，即在计算纵向受拉非预应力筋的应力时，采用荷载准永久组合而不是旧规范的标准组合，并将反映裂缝间混凝土伸长对裂缝宽度的影响系数αc从旧版规范的0.85降低为0.77。新规范之所以做出这样的调整，使得裂缝宽度计算较旧规范略有放松，主要是考虑到我国现阶段要大力推广应用 500 MPa 高强钢筋这一现实需求，裂缝宽度计算公式如下：

(3)

(4)

式中：αcr为构件受力特征系数；ftk为混凝土轴心抗拉强度标准值；ψ为钢筋应变不均匀系数；其余参数与水运工程规范相同。

1.3 公路规范

《公路钢筋混凝土及预应力混凝土桥涵设计规范》采用数理统计公式，通过对影响混凝土构件裂缝宽度因素的分析及国际上的统一认识，在旧版规范计算公式的基础上进一步改进后得到的，裂缝宽度计算公式如下：

(5)

式中：C1为钢筋表面形状系数；C2为长期效应影响系数；C3为与构件受力性质有关的系数；σss为由频遇组合引起的纵向钢筋应力；其余参数与水运工程规范相同。

1.4 水工规范

《水工钢筋混凝土结构设计规范》[6]采用黏结滑移-无滑移综合理论，裂缝宽度计算公式是根据低强钢筋试验分析给出的[7]，裂缝宽度计算公式如下：

(6)

式中：α为构件受力特征和荷载长期作用的综合影响系数；σsk为按荷载标准值计算的纵向钢筋应力；其余参数与水运工程规范相同。

2 裂缝宽度计算对比

2.1 实例1

设梁截面为宽300 mm、高500 mm，为便于分析，各规范在计算时采用相同的材料参数和相同的内力，比较钢筋应力、保护层厚度与裂缝宽度的关系，如图1所示。

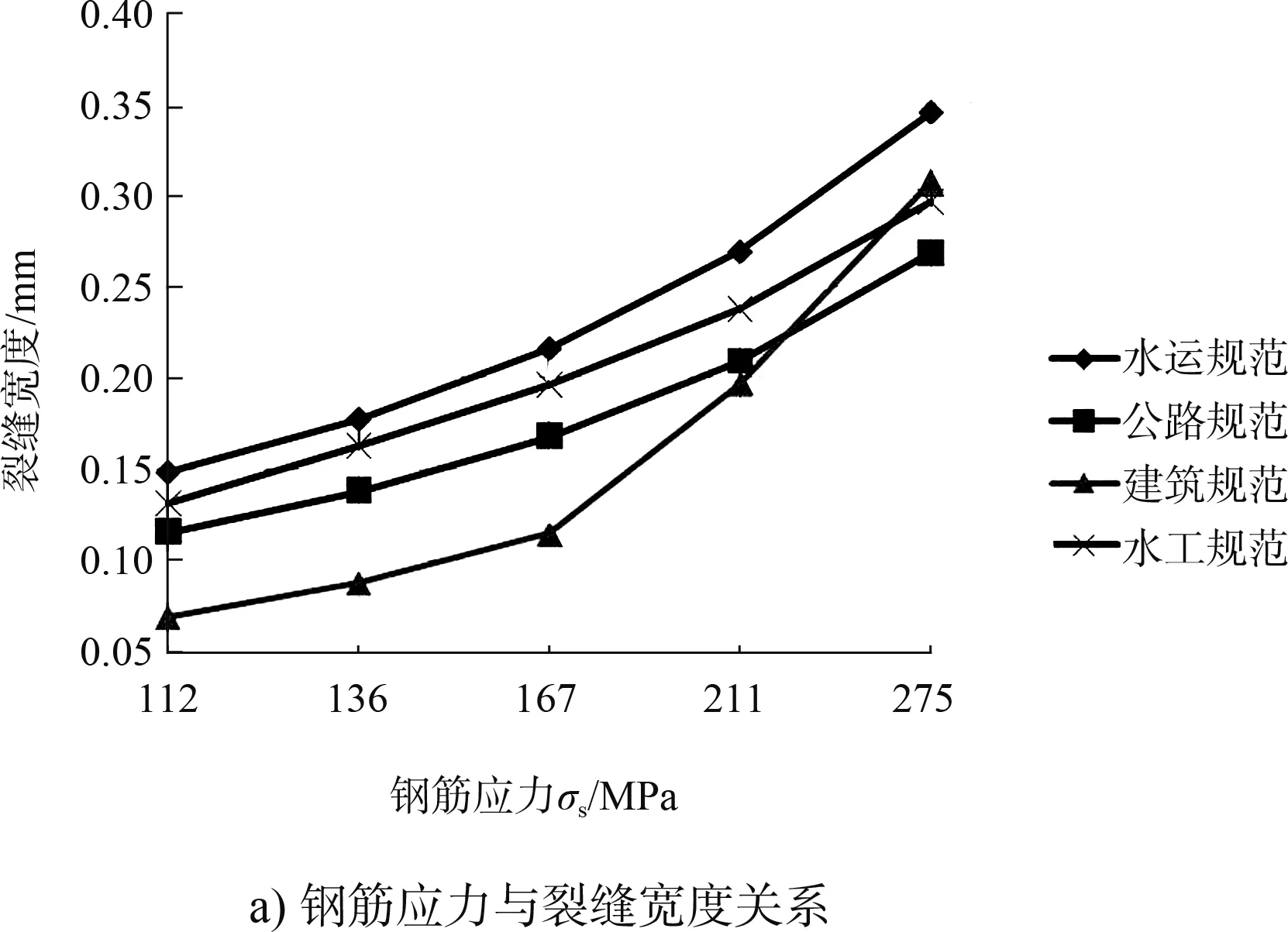
图1 钢筋应力、保护层厚度与裂缝宽度的关系

由图1可以看出，裂缝宽度与钢筋应力、保护层厚度之间变化趋势是一致的，裂缝宽度随钢筋应力的增大而增大，随钢筋保护层的增大而增大，但在相同条件下，水运规范计算的裂缝宽度最大，裂缝宽度值是建筑规范的2倍，是公路规范的1.28倍，是水工规范的1.1倍。出现这种情况的主要原因是水运规范和水工规范均为根据低强钢筋试验分析统计的，而建筑规范和公路规范均根据最新的试验分析统计的。文献[8]将水运工程规范与英标BS 8110-2、美标ACI 318-95、欧标EN 1992-1-1、欧标CEB-FIP进行了对比，结果也表明，水运工程规范计算值偏大，最大值可以达到最小值的2倍。

2.2 实例2

设一简支梁，跨度为6 m，梁截面为宽350 mm、高550 mm，混凝土强度等级为C30，裂缝宽度限值为0.2 mm，活荷载标准值分别取3、10、20 kPa，纵向受力钢筋分别采用HRB335、HRB400、 HRB500，各规范计算所需钢筋面积见表1，为便于分析，各规范在计算时采用相同的材料参数和相同的内力。

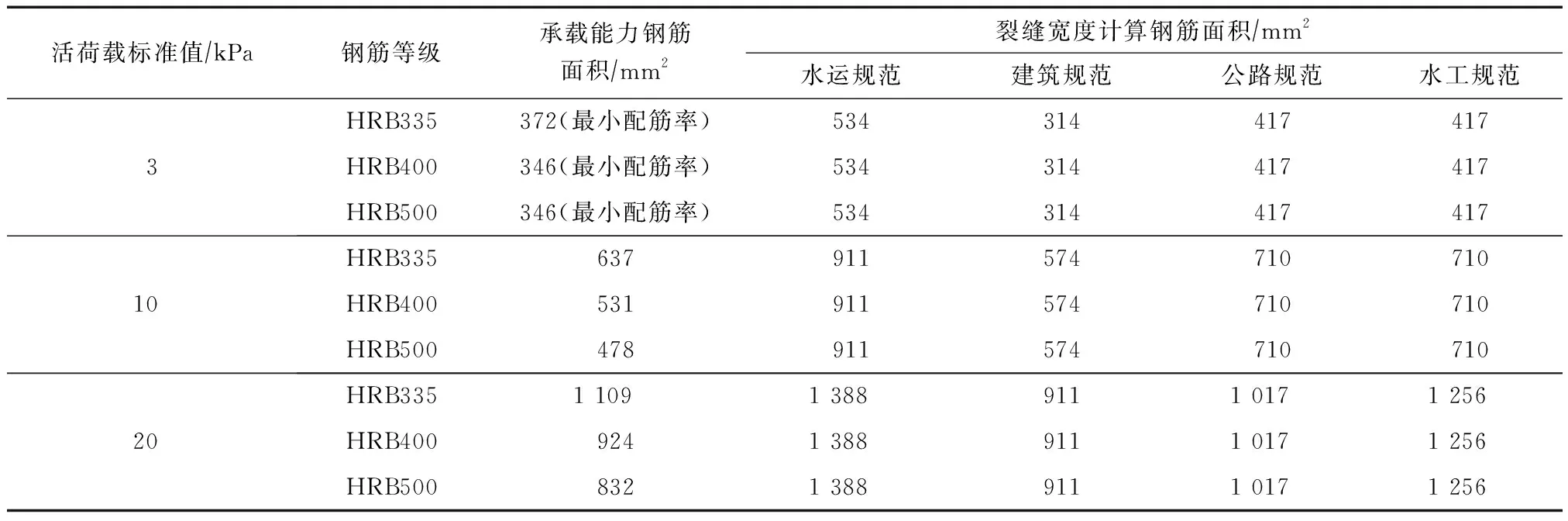
表1 不同活载下简支梁不同规范配筋计算比较

由表1可看出，相同荷载条件下，水运规范计算所需的钢筋面积最大，且均为裂缝宽度控制截面配筋面积，所需钢筋面积与钢筋等级无关，建筑规范计算所需的钢筋面积最小，采用HRB500级钢筋比采用HRB335级钢筋最大可节省18%的钢材，公路规范计算所需的钢筋面积居中，采用HRB500级钢筋比采用HRB335级钢筋最大可节省8%的钢材，水工规范的裂缝宽度计算公式由于也是根据低强钢筋试验分析给出的，所需钢筋面积与水运规范一样，均为裂缝宽度控制截面配筋面积。

由以上两个实例可看出，水运规范裂缝宽度计算结果最大，且一般裂缝要求控制截面配筋，在设计中虽然采用高强钢筋，但钢筋用量基本不变，使高强钢筋材料性能未能充分发挥，主要原因是规范中最大裂缝宽度仍采用旧规范公式，未考虑钢筋强度增高的影响。国内对高强钢筋混凝土构件裂缝宽度计算公式进行了一系列的研究[9-10]，根据近年来国内多家单位完成的配置400、500 MPa 带肋钢筋的混凝土梁裂缝宽度加载试验结果，试验平均裂缝宽度值均小于旧规范计算值，因此须根据试验结果对裂缝宽度计算公式进行调整。

3 建议计算公式及对比分析

3.1 建议计算公式

文献[10]的研究表明，混凝土开裂后，在主裂缝间的混凝土会出现次裂缝，次裂缝一方面减弱了混凝土与钢筋的黏结应力，增大了钢筋应变不均匀因数；另一方面，次裂缝也会增大主裂缝间混凝土的变形，减小了主裂缝的宽度，显然，随着钢筋应力的增大，次裂缝会增多，钢筋应变不均匀系数可以间接反映次裂缝的开展情况，钢筋应变不均匀系数变大，次裂缝发展得越多，因此，建议在规范公式中引入钢筋应变不均匀系数ψ，本次考虑ψ取建筑规范中钢筋应变不均匀系数，随着研究的深入可修正该系数，建议计算公式如下：

(7)

其中ψ的计算公式与式(4)相同。

3.2 对比分析

由于文献[7]、[9]～[11]推荐公式、建筑规范计算公式均是基于大量试验数据的基础上统计而来的，具有一定的合理性、可靠性，为了对比分析式(7)的合理性，本文采用以上公式进行对比。

杜毛毛得到的配置高强钢筋受弯构件最大裂缝宽度计算公式建议为：

(8)

周建民等得到的配置高强钢筋受弯构件最大裂缝宽度计算公式建议为：

(9)

李志华等得到的配置高强钢筋受弯构件最大裂缝宽度计算公式建议为：

(10)

朱尔玉等得到的配置高强钢筋受弯构件短期最大裂缝宽度计算公式建议为：

(11)

(12)

以上各式中参数与建筑规范相同。

采用实例1的相关数据，式(7)计算的钢筋应变不均匀系数ψ值见表2。可以看出，钢筋应变不均匀系数ψ值随钢筋应力的增大而增大。

表2 不同钢筋应力下钢筋应变不均匀系数ψ值

采用实例1的相关数据，采用式(7)计算的裂缝宽度与以上各建议公式及建筑规范公式的对比结果见图2。

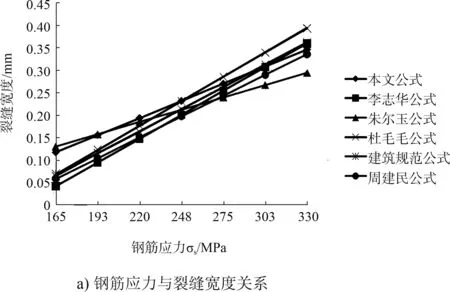
图2 钢筋应力、混凝土强度与裂缝宽度关系

由图2a)可看出，当钢筋应力较大时(σs>250 MPa)，式(7)计算结果与式(8)～(10)结果平均值一致，与建筑规范结果差别稍小，当钢筋应力较小时(σs<250 MPa)，式(7)计算结果均大于各式计算结果。

由图2b)可看出，随着混凝土强度等级的提高，裂缝宽度随之减小，混凝土强度等级从C30增加至C55时，式(7)计算的裂缝宽度减小了10%左右，式(7)计算的裂缝宽度减小了5%左右，其他公式计算的裂缝宽度减小了近30%，式(7)计算的裂缝宽度减小值适中。

采用实例2的相关数据，式(7)与以上各建议公式及建筑规范公式对比结果见表3。

表3 不同活载下简支梁不同公式配筋计算比较

由表3可看出，相同荷载条件下，式(7)计算所需的钢筋面积仍较大，但裂缝宽度不控制截面配筋面积，采用HRB500级钢筋比采用HRB335级钢筋最大可节省11%的钢材，式(8)～(11)计算所需的钢筋面积较小，且结果一致，采用HRB500级钢筋比采用HRB335级钢筋最大可节省29%的钢材。

从以上两个例子可以看出，提出的建议公式(7)与文献[7]、[9]～[11]推荐公式、建筑规范计算公式相比，采用高强钢筋时，钢筋用量有所降低，但降低的幅度不是太大，便于过渡时使用。

4 结论

1)水运规范裂缝宽度计算结果最大，且一般裂缝要求控制截面配筋，在设计中虽然采用高强钢筋，但钢筋用量基本不变，限制了其强度的发挥，不利于高强钢筋的推广。

2)根据相关研究结果，建议对水运规范中混凝土构件裂缝宽度进行修正，鉴于目前针对水运工程高强钢筋应用试验较少，本次修正建议将规范中计算公式乘以折减系数ψ。

3)本文主要根据相关文献及规范对水运规范裂缝宽度计算公式提出初步的修改建议，建议下步开展相关专项研究工作，以便确定更加合理的计算公式。

4)目前，国内各规范计算裂缝宽度的公式不尽相同，下一步建议根据各规范修订情况，国内公式尽量统一。