贷款利率的成本加成模型的应用研究

靳海娟

（长治学院数学系，山西长治 046000）

随着国家经济的飞速发展，各种行业迅速发展起来。而任何商业的发展都需要一定的本金，这种情况造就了贷款现如今成为商业银行的重要盈利项目。同时建立怎样的贷款模型也成了商业银行重点关注的问题，因此贷款定价也就成了重中之重。贷款定价就是银行依据自身条件，通过全面计算贷款能够为银行带来的利润，考虑贷款带来的各种等因素，对贷款是否有盈利性、安全性和市场竞争力要求的综合价格的过程[1]。而影响贷款利率的定价的因素有下面几种（如图1）。

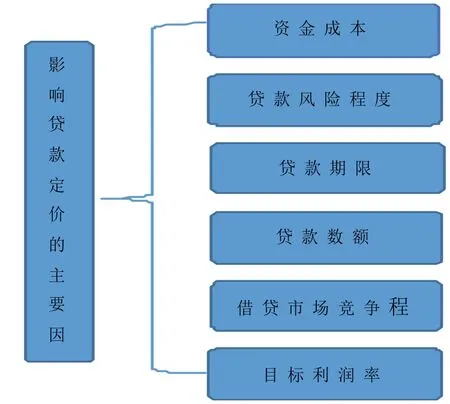
图1 影响贷款定价的主要因素

此外，当贷款成为商品时，它的类型就不会单一，所以在确定每一种贷款的价格时，要对其进行符合自身利益的定价，故贷款定价也要遵循一定的原则，正如摘要提到的三高原则，下面对一些变量进行确定：

P——贷款利率；

C1—资金成本；

C2—风险成本；

C3—贷款费用；

C4—机会成本；

R1—银行贷款的目标收益率；

R2—借款人拟投资项目的预期收益。

贷款利率由以上因素等决定，在以上因素的前提下建立贷款利率的定价模型[2]：

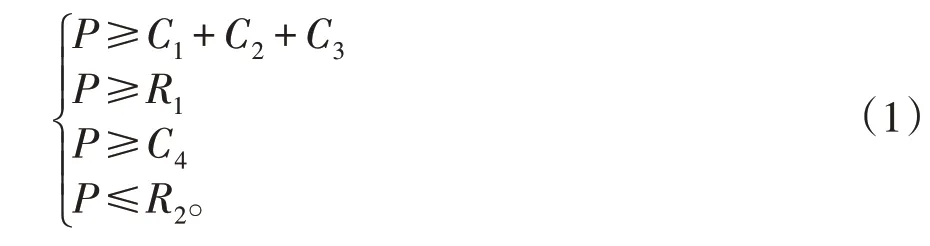
贷款利率需满足（1）条件，并在定价过程中依据贷款发放的情况最终确定它的值；银行的定价只有符合了不等式组（1），就可以抵消信用风险和经营所花的费，那么银行就可以获得收益。

1 成本加成模型

成本加成方法是跟成本有关的定价模型，成本决定它的利率，该模式的贷款的利率包括以下四部分[3]：

①贷款资金的筹集成本；

②贷款费用；

③风险补偿费。违约风险和期限风险的总和。

④目标利润。即银行要求的最低利润。

因此这个模式可以表示为[4]：

贷款利率=筹资成本+贷款风险补偿率+目标利润率+贷款费用率

单利和复利是利息问题中最常用的两种计算方法。而该模型运算时会遇到单利（Single interest）：

设投资初始值为1，其中在每时段利息为常数，则得到线性累积函数[5]：

a(t)=1+it，对于整数t≥0，

其中a(t)表示累积函数，也表示在t时刻本金和利息的和。当一个单位的初始投资达到t+s时期所得的利息a(t+s)-1，等于t个时期得到利息与经过s个时期得到的利息之和[6]。

a(t+s)-1=(a(t)-1)+(a(s)-1),

即

a(t+s)=a(t)+a(s)-1∀t,s≥0,

因累积函数具有连续性，由初始条件：a(0)=1，a(1)=1+i，由导数定义得：

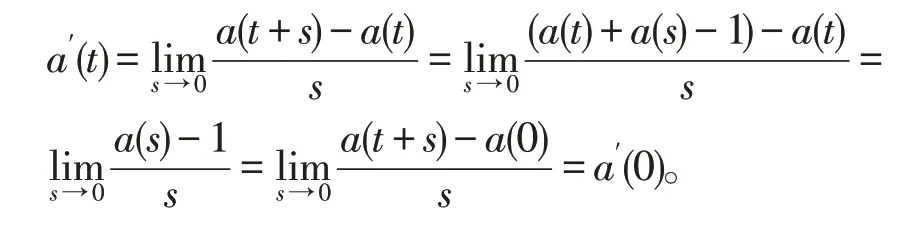
在上式用r代替t，并将等式两端从0 到t积分，就有

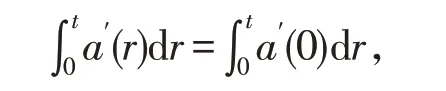
即a(t)-a(0)=t∙a′(0)，

a(t)=1+t∙a′(0)，

若t=1，则有

a(1)=1+i=1+a′(0)，

因而a′(0)=i代入原式得：

a(t)=1+i∙t∀t≥0，

故等式成立。

以上贷款定价模型的应用可以确保银行每笔贷款都可以获得收益，但却会使它的的竞争力降低，从而导致客户流失和贷款市场份额的萎缩。此外，银行在使用这一类模型的前提条件就是具备一套完善的成本管理系统和贷款风险管理系统，而文章后面的应用都是在理想状态上进行的。

2 成本加成模型的应用

2.1 关于成本加成模式的公式中各部分变量的确定

2.1.1 贷款利率P

贷款利率=筹资成本率+贷款费用率+贷款风险补偿率+目标利润率。

2.1.2 筹资成本率Ma

筹资成本率一般用平均筹资成本率来表示，平均筹资成本率用筹资均摊利率和筹资业务费率的和来表示。

即：平均筹资成本率=等资成本率+等资业务

费用率，用Ra表示筹资均摊利率，用Ta表示筹资业务费用率，则公式为：

Ma=Ra+Ta，

其中筹资均摊利率Ra计算公式为：

筹资业务费用率Ta是指银行为筹集资金而付出的可变费用与盈利资产余额的比率[1]。

故筹资业务费用率计算公式为：

2.1.3 贷款费用率

贷款费用率是间接费用率和直接业务费用率的和，

即：

贷款费用率=间接业务费用率+直接业务费用率用Mc和Md分别表示间接费用率和直接业务费用率，则公式为：

Mb=Mc+Md,

间接费用率Mc公式表示为：

间接费用率=[固定费用+（总可变费用-筹资部门可变费用-贷款部门可变费用）]/盈利资产余额*100%,

即：Mc=,

其中公式中的字母分别表示对应的费用。

直接业务费用率Md是指银行贷款部门为了贷款业务活动的开展而在一定时间内发生的可变费用Hb与贷款资产余额Y的比率[1]。则公式表示为：

即：Md=×100%。

2.1.4 贷款风险补偿率Ms

由于市场化，基准率不再确定，而是由市场决定，银行可以内部确定作为银行内部资料，在具体定价时使用，表1为我国某商业银行的期限风险补偿率估算表：

表1 期限风险补偿率估算表

违约风险补偿率只需根据对贷款客户评定的信用等级结合期限风险补偿率估算表即可，例如表2为国内某商业银行违约风险补偿率估算表：

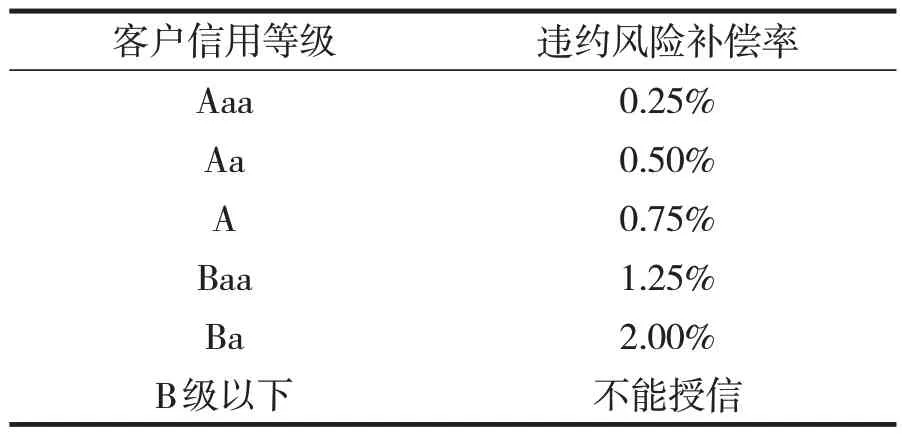
表2 违约风险补偿率估算表

2.1.5 目标利润率M

目标利润率就是银行的最低收益率，而西方商业银行一般定在10%以上。例如华夏银行的最低经济资本回报率为12.69%。

利用上述公式和计算方法，皆可以算出这个模型下的贷款利率P。

2.2 成本加成模式的应用

例1 某Aaa级公司向银行Q借入金额为1 000万元的一年期流动资金贷款，且银行Q 在2015 年全部资产余额为185 162 800.00 万元，其中盈利资产余额X为96 611 824.56 万元，贷款资产余额Y为90 510 511.14 万元，全部负债利息总额为16 72 301.02万元，筹资部门可变费用支出额Ha为18 456.16 万元，贷款部门可变费用支出额Hb为15 004.62 万元，总可变费用H为181 922.10 万元，在一定时期内的固定费用F为84 827.26万元，目标利润率为12%。则对应变量为：

（1）确定平均筹资成本率Ma。

由前面可知：Ma=Ra+Ta，

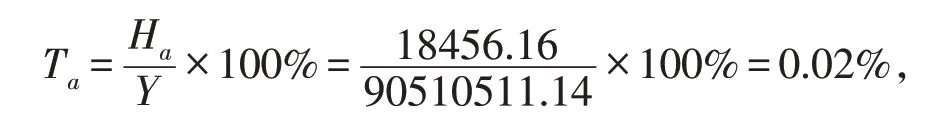
计算可得平均筹资成本率为：

Ma=Ra+Ta=1.85%+0.02%=1.87%。

（2）确定贷款费用率Mb。

Mb由间接费用率Mc和直接业务费用率Md组成[1]，其中：

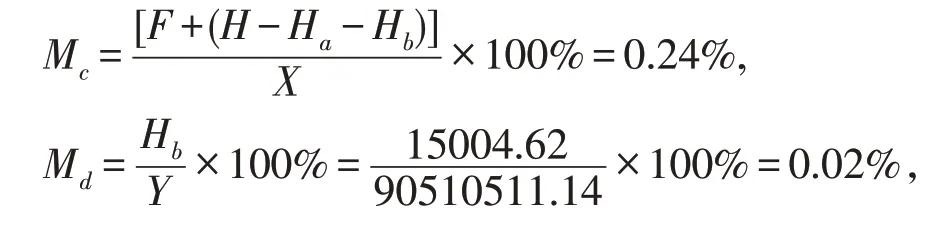
于是得营业费用率为：

Mb=Mc+Md=0.24%+0.02%=0.26%。

（3）确定贷款风险补偿率Ms。

这笔贷款是年限为1年的流动资金贷款，需要加上风险溢价，由表1 可知，这笔贷款需要加上0.04%的期限风险补偿率。

由题可知道该银行是Aaa 级企业，由表2 得，这笔贷款需要加上0.25%的违约风险补偿率。

故这笔贷款的风险补偿率为：

Ms=0.04%+0.25%=0.29%。

（4）确定贷款利率P。

由以上计算结果代入公式可得贷款利率为：

P=Ma+Mb+Ms+M=1.87%+0.26%+0.29%+12%=14.42%，

则成本加成模式的贷款利率为14.42%。

3 结语

如今，随着金融的市场化，我国的利率制度也逐渐向完全市场化的自由利率制度转变，通过前文的分析与研究我们可以看到贷款利率当然定价过程十分复杂，影响其因素的也有很多。同时通过本文的论述，可以看到上述模型都是在很大程度上结合主、客观各种条件，仔细判断内、外各种因素后建立的。如果我国银行建立贷款利率定价模型，个人认为需要结合模型的特点，建立一个具有盈利性和服务型贷款定价模型。现如今，我国商业银行成本核算还没有达到分部门、分产品、分用户核算，贷款风险测试制度依旧用的是过去的方法，准确度比较低，这都会影响贷款定价体系的建立和完善[2]。因此只有建立全面完整的成本管理和风险预测制度，才能用来支持商业银行建立科学，完善的贷款定价模型，使贷款定价可以充分体现贷款所承担的各种风险和经营费用，保证目标收益的实现[7-10]。