湖北城市创新效率测评与提升策略研究

2020-11-06张静刘威

社会科学动态 2020年10期

张静刘威

摘要：通过构建创新效率评价指标体系，使用2013—2017年市州面板数据，采用三阶段DEA测算湖北长江经济带各市（州）创新效率，结果发现：（1）从空间格局看，武汉、宜昌、襄阳、鄂州、黄石的创新综合效率位于前列，而恩施、仙桃、潜江和天门等市则处于末端。（2）从时间演变看，综合技术效率变化趋势存在区域差异，各市（州）变化趋势大致可以分为稳定型、上升型和下降型。基于以上结论，提出综合施策优化城市创新生态、构建产学研良性互动循环、优化各类人才“引用留育”机制和完善创新投入机制等对策建议。

关键词：创新效率;三阶段DEA;湖北长江经济带

基金项目：湖北省软科学研究项目“湖北长江经济带城市创新效率评价与提升策略”（项目编号：2019ADC129）;湖北省重大调研课题基金项目“湖北省技术创新驱动产业升级发展的热点、难点及对策研究”（项目编号：J23）

中图分类号：F014.7 文献标识码：A 文章编号：2096-5982（2020）10-0087-09

引言

创新能力是促进区域经济增长和增加区域竞争能力的关键要素，而创新效率的高低综合反映区域创新系统对资源的配置能力与使用效率，进而成为评价该区域能否持续、高质量发展的重要标准。2018年4月，习近平总书记在武汉主持召开深入推动长江经济带发展座谈会时明确提出：以长江经济带发展推动经济高质量发展。湖北是长江干线流经里程超千公里的唯一省份，科学评价湖北长江经济带城市创新效率，对湖北塑造更多依靠创新驱动、更多发挥先发优势的引领型发展，走在长江经济带高质量发展前列具有重要的实践价值。

从已掌握的文献资料看，目前的研究主要集中在以下两个方面：

一是关于不同测度方法比较研究。创新效率测度方法主要有以随机前沿模型（SFA）方法为代表的参数方法和以数据包络分析（DEA）方法为代表的非参数方法。随机前沿分析（SFA）方法是评测决策单元有效性的常用方法。李婧在考虑空间效应的基础上，应用随机前沿模型对各地区创新效率进行实证测评与分析①。曹霞结合投影寻踪模型处理高维数据的特点，改进随机前沿模型，对中国各区域创新效率及影响因素进行实证分析②。数据包络分析（DEA）方法是评价多投入—多产出模式下决策单元间相对有效性较为常用的方法。时鹏将③、孙凯④等运用DEA模型对我国区域创新效率进行静态分析。随着对区域创新过程及创新價值链理解的逐步深入，既关注区域创新科技投入产出情况，又关注科技成果经济转化情况的二阶段DEA模型受到关注，如冯志军⑤等。刘凤朝⑥、徐小钦⑦、韩先锋⑧、刘明广⑨等分别基于DEA的Malmquist指数法对创新效率进行动态分析。李兰冰⑩基于DEA模型和Tobit模型、陈伟{11}基于规模报酬可变的链式关联网络DEA模型、刘伟{12}将三阶段DEA模型与Bootstrap方法相结合、分别对我国省级区域创新效率进行测算与比较分析。

二是关于区域创新效率实证研究。国内学者基于省际面板数据，对各省区的创新效率值进行测算、评价与比较，研究成果颇丰。刘顺忠{13}、池仁勇{14}、官建成{15}分别采用DEA方法实证测算了中国各省区的创新效率值，并考察影响创新效率的关键因素。岳书敬{16}等应用SFA方法研究1998—2005年我国区域研发效率差异及其影响因素。

由上述研究可以看出，无论是从研究方法还是从研究范围上，学者对我国区域创新效率问题都已进行了较为全面深入的探索。同时，已有研究对创新效率的评价多侧重于国家及省际之间，对省内各城市创新效率的研究不多，而恰恰是省内各城市的创新效率影响了省级层面的整体创新能力。学者大都对创新进行阶段划分，但是对研发资本存量在创新过程中起到的累积作用、创新产出对下一次创新产生影响等涉及较少。因此，本文选择三阶段DEA，引入资本存量指标，以湖北省各市（州）为对象分析其创新效率，旨在为政府制订有效的区域发展政策、合理配置创新资源、提高区域创新能力提供科学的理论依据，以创新推动长江经济带高质量发展。

一、方法与数据

（一）研究方法

本文采用三阶段DEA模型测算湖北省16个市（州）创新效率。考虑创新过程的连续性，引入资本存量作为创新投入指标，构建创新效率评价指标体系。根据Fried等提出的模型，三阶段DEA构建过程如下：

第一阶段：利用BCC模型测算效率值。经典的DEA模型分为CCR模型和BCC模型。CCR模型是假设规模报酬不变，而BCC模型则可以处理规模报酬变动下的效率问题，且BCC模型计算的综合技术效率可以进一步分解为纯技术效率和规模效率，这有助于分析区域创新效率受纯技术因素或规模因素影响。由BCC模型计算出投入变量的松弛变量，作为第二阶段的投入变量。

第二阶段：构造相似SFA模型。Fried等（2002）指出第一阶段的投入松弛量是由管理无效率、环境因素和随机噪声造成的。第二阶段以第一阶段求出的松弛量为因变量，以环境因素为自变量，通过构建相似SFA模型，将环境影响和随机噪声剔除，仅保留管理无效率造成的投入松弛。

以投入变量的松弛量为因变量，环境因素为自变量，构造模型，如式（1）所示：

Sni=f（Zi;βn）+νni+μni;i=1，2，3……，n=1，2，3……（1）

其中，Sni是第i个决策单元第 n项投入的松弛值;Zi是环境变量，βn是环境变量的系数;νni+μni是混合误差项，νni表示随机干扰，μni表示管理无效率。其中ν是服从N（0， σν2）是随机误差项，表示随机干扰因素对投入松弛变量的影响;μ是管理无效率，表示管理因素对投入松弛变量的影响，假设其服从在零点截断的正态分布，即μni服从N+（0， σν2），νni和μni不相关。采用极大似然技术估计未知参数，剔除环境因素和随机因素对效率测度的影响，以便将所有的决策单元调整于相同的外部环境中。调整公式如下：

ΧniA=Χni +[maxi（Zn）- Zin]+[maxi（ni）-ni

n=1，2，3……，N;i= 1，2，3……，I （2）

其中，ΧniA是調整后的投入，Χni 是调整前的投入;[maxi（Zin）- Zin]是对外部环境因素进行调整;[maxi（ni）是将所有决策单元至于相同运气水平下。

上式中，ni可由条件估计？魯[ni丨ni+μni]估计得到。？魯[ni丨ni+μni ]可以根据下面公式计算得出：

？魯[νni丨νni+μni]= Sni- Znin-？魯[μni丨νni+μni] （3）

第三阶段：调整后的BCC模型。在第三阶段，利用经过第二阶段调整后的投入和原始产出重新带入BCC模型进行效率测算。由于剔除了环境因素和随机噪声的影响，调整后的效率值能更为客观准确地反映决策单元的创新效率水平。

（二）变量选择

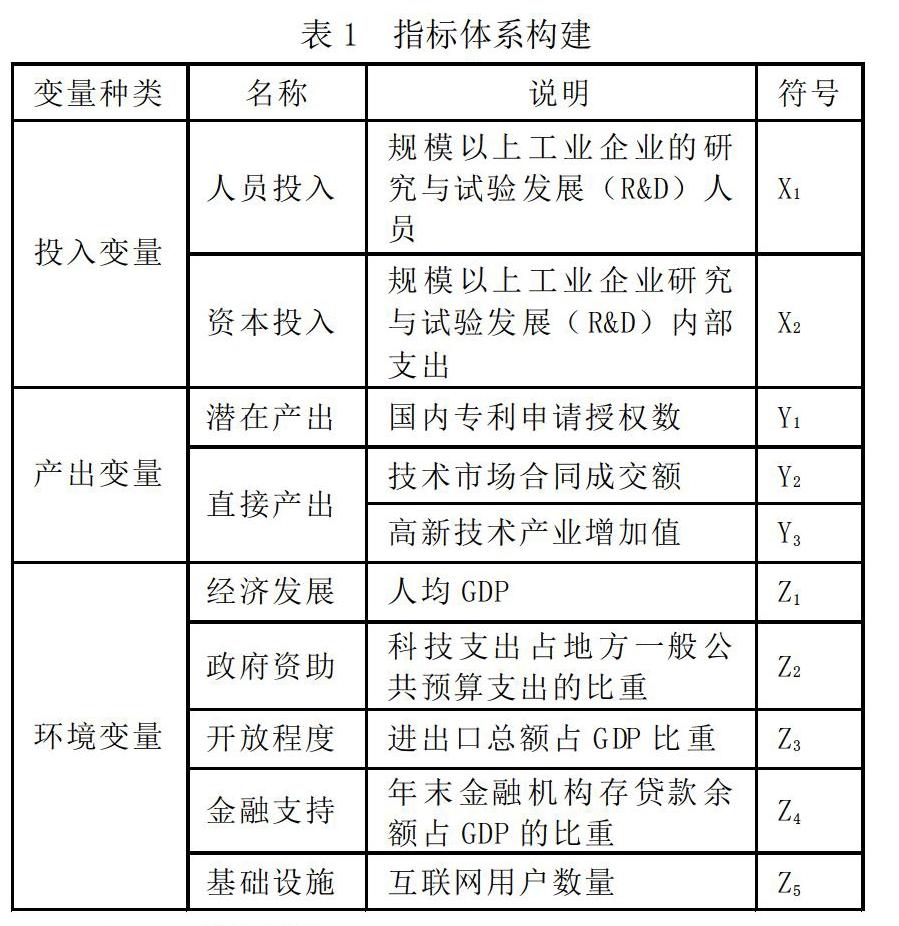
一般而言，运用三阶段DEA模型进行效率测算时，应明确对应的指标体系。本文从投入、产出和环境变量三个维度来构建区域创新效率的变量体系。

1. 投入变量

劳动力和资本是经济投入产出系统研究中的两个基本投入。在对区域创新效率进行测度时，其投入也可以从这两个方面来衡量。（1）在人员投入方面，本文主要采取了规模以上工业企业的研究与试验发展（R&D）人员X1来衡量研究与试验发展（R&D）人员的实际投入水平。鉴于十堰和潜江市相关指标数据的缺乏，本文分别采用科学家和工程师人员数、科学研究与技术服务业从业人员予以代替。（2）在资本投入方面，本文采取规模以上工业企业研究与试验发展（R&D）内部支出X2衡量规模以上工业企业研究与开发机构当年用于企业内部的实际支出。

2. 产出变量

本文从区域创新创造的价值或潜在价值方面选择。国内专利申请授权数（Y1）代表区域创新能力的潜在产出，技术市场合同成交额（Y2）和高新技术产业增加值（Y3）代表区域科技创新能力的直接产出，反映区域科技与经济相结合、技术成果转化为市场价值的水平。

3. 环境变量

环境变量是指对创新效率产生影响但不是决策单元可控制的因素。本文从五个方面考虑影响地区创新效率的环境变量。

（1）经济发展。地区经济发展与创新投入密切相关。地区经济发展水平越高，创新投入也会越多，因而也越有能力进行创新活动。本文采用地区人均GDP（Z1）来表征区域经济发展水平。

（2）政府资助。政府对创新活动的资助主要体现在实行拨款资助和税收优惠等政策来扶持创新活动，降低企业开展研发创新活动的成本和风险，激发企业开展研发创新的积极性。本文选用科技支出占地方一般公共预算支出的比重（Z2）来表征政府资助这一指标。

（3）开放程度。对外开放是保障区域可持续发展重要因素。本文用各区域进出口总额占GDP比重（Z3）来表征区域开放程度。

（4）金融支持。金融机构为创新活动提供资金支持，亦为创新主体提供金融信息和咨询服务。本文采用区域年末金融机构存贷款余额占GDP（Z4）的比重来表征其对创新金融环境的支持。

（5）基础设施。区域创新中基础设施的能为创新提供必要的物质、交通、信息等支撑条件，基础设施条件越完备越有利于创新的发生。考虑数据的可获取性，本文选取互联网用户数量（Z5）来表征区域基础设施发展水平。

（三）数据来源

本文原始数据来源于2014—2018年《湖北省统计年鉴》和湖北省各个市州（不含神农架林区）的《统计年鉴》，研究对象为湖北省16个市（州）（神农架林区数据不全，分析中暂时不予考虑）。文中的投入、产出和环境变量如表1所示。其中个别缺失数据本文采用线性插值法补齐。

二、测算与分析

遵循三阶段DEA的分析步骤，本文分三步给出每阶段的估计结果。

（一）第一阶段DEA结果

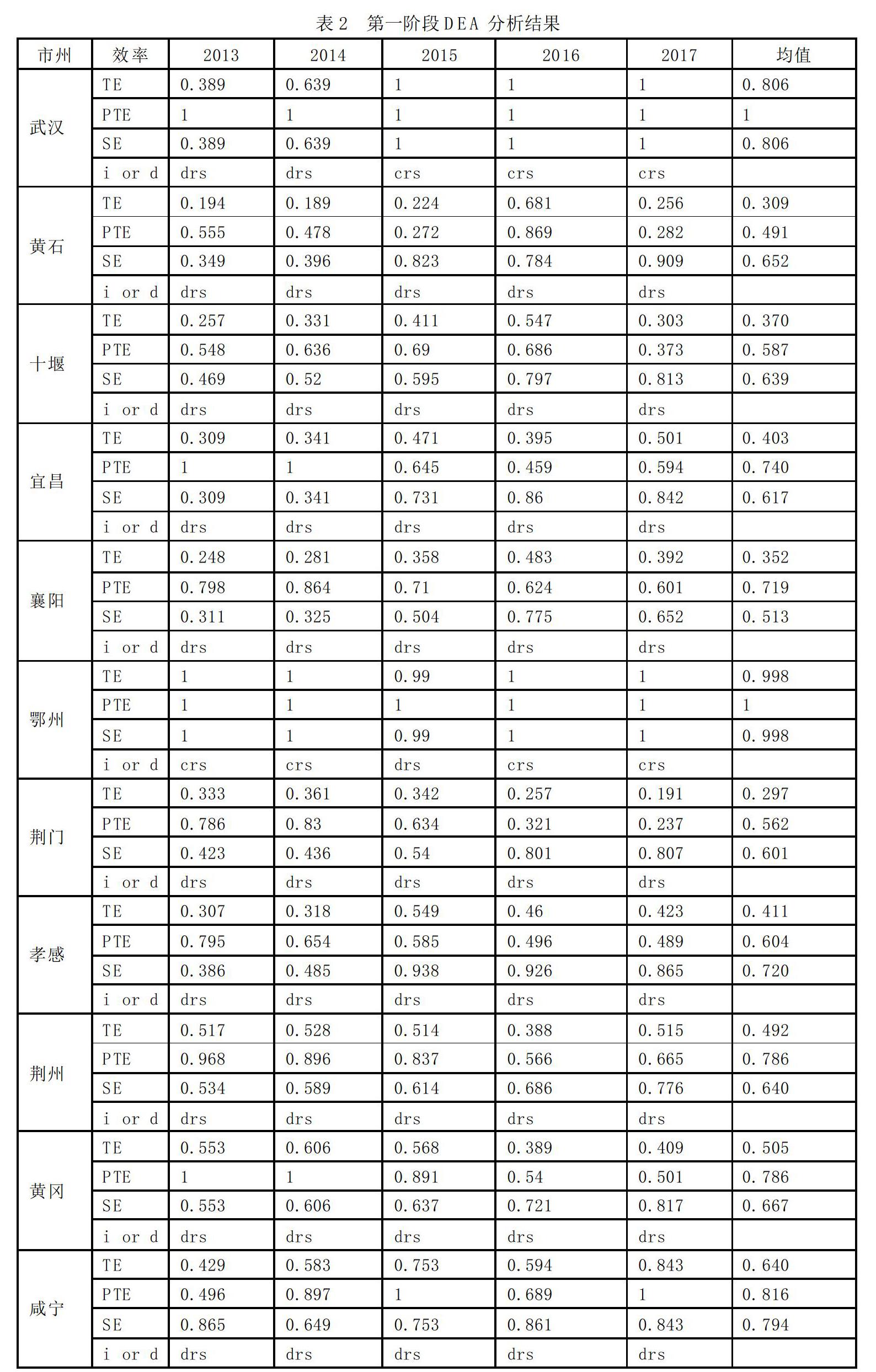
在第一阶段，通过所获取的相关数据，借助软件DEAP2.1，选择BCC模型，对2013—2017年湖北省16个市州的创新效率水平进行了测度。其中综合技术效率（TE）反映各个市州的综合绩效;纯技术效率（PTE）反映剔除规模报酬影响后的各个市州的创新技术效率，也可以理解为受管理水平和技术影响的生产效率;规模效率（SE）是指各个市州投入规模变化对综合技术效率的影响，反映各个市（州）创新规模的优化程度。结果如表2所示。

省域创新效率分析。2013—2017年，湖北省整体创新综合效率和纯技术效率均呈现先上升后下降的倒“U”型特征，规模效率呈现稳步上升趋势。其中综合效率均值为0.608，纯技术效率均值为0.781，规模效率均值为0.768。2013—2014年，综合效率、纯技术效率和规模效率均呈现上升趋势，且规模效率要低于纯技术效率，说明该时段纯技术效率和规模效率均促进了综合效率的提升，且造成综合效率水平低下的主要问题是规模效率偏低。从2015年开始，综合效率呈现先增后减的趋势，纯技术效率开始递减，规模效率则递增，且规模效率已经高于纯技术效率，说明该时段主要是由规模效率促进综合效率的提升，而纯技术效率则造成综合效率下降且处于较低水平。

规模报酬分析。2013—2017年，16个市（州）共80个评测单元中，处在最沿面的有22个，其中有1个规模报酬递减，21个规模报酬不变。非有效单元有58个，其目标值有5个是规模报酬递增，53个规模报酬递减。整体来看，规模报酬递减的有54个，占比67.5Z%，规模报酬递减的有5个，占比6.25%。可见，实现规模报酬递增的市（州）很少，说明各个市（州）的创新规模没有实现最优状态，且近年来这种状态没有得到明显改善。

地级市差异分析。（1）从时间趋势看，鄂州、恩施连续五年达到效率前沿面;武汉、潜江和天门的创新效率呈现上升势态，分别在2015年和2016年达到效率前沿面;仙桃从2013—2016年连续4年处于效率前沿面，于2017年开始下降。黄石、十堰、宜昌、襄阳、孝感和咸宁呈现出螺旋上升势态;荆门呈现出逐步下降趋势;荆州、黄冈和随州均呈现出波动变化，且处于无效率状态。（2）从空间格局看，效率值较高的地区分别是武汉、鄂州、恩施、仙桃和潜江，较低的地区有黄石、十堰、宜昌、襄阳、荆门和孝感。可以看出，各市（州）创新效率值的空间分布与各自的经济发展水平并不完全一致。因此，本文认为DEA的测算结果可能存在偏差，这种偏差的原因可能在于没有考虑各个市（州）的环境差异。三阶段DEA可以有效克服这一缺陷。

（二）第二阶段SFA回归结果

通过SFA回归，可以剔除环境因素和随机噪声的影响。基本思路是将各个投入指标的松弛变量作为因变量，环境指标作为自变量，进行SFA分析。回归分析结果如表3所示。

从表3来看，2个投入的松弛变量均通过LR检验，说明整体来看外部环境明显影响投入松弛变量。gamma值分别为0.824和0.69，且均在1%水平下显著，说明在各个决策单元中管理无效占主要因素。因此，为剥离管理因素和随机因素，对投入变量进行第二阶段的调整显得十分重要。

在考察环境变量对投入松弛量所带来的影响时，若系数是正数，则意味着环境变量数值上升将会使投入的松弛变量增长，或者使得产出下降，造成浪费，对环境效率产生不利影响;若系数是负数，则表明，环境变量数值上升将会使得投入松弛量下降，产出增加，产生节约现象，对环境效率产生有利影响。下面具体分析对投入松弛变量产生显著影响的环境变量：（1）经济发展水平。经济发展与R&D内部支出的松弛变量回归结果在1%的置信水平下显著为正。说明经济发展对与R&D内部支出的投入冗余带来的影响是显著的，经济发展水平的提高会使得R&D内部支出投入冗余上升，从而降低R&D内部支出的利用效率。（2）政府资助。政府资助与R&D内部支出的松弛变量回归结果在1%的置信水平下显著为负，这说明政府资助对R&D内部支出的投入冗余具有负向影响，政府资助增加使投入的冗余降低，有利于资源的合理利用，提升决策单元的创新效率。（3）开放程度。开放程度与R&D内部支出的松弛变量回归结果在1%的置信水平下为正。这说明开放程度的增加将会导致投入冗余的增加，造成资本投入的浪费现象。

基于上述分析，各个环境要素对决策单元的影响并不完全一致。如果不控制这些环境因素，就使得决策单元处于不同的环境之中，从而造成效率估计结果误差。本文应用相应的公式对原有投入变量进行调整，从而剥离环境因素和随机噪声的影响，使各个决策单元处于相同的外部环境条件下，以便提高估计结果准确性。

（三）第三阶段调整后DEA结果

上述第二阶段得到剔除环境因素和随机噪声后的原始投入的调整值，本部分将调整后的投入值和原始产出值再次带入传统DEA模型之中进行分析，得到第三阶段各个市（州）的创新效率和规模报酬状态，如表4所示。

调整前后效率值比较。（1）从整体趋势看，综合效率由调整前的先上升后下降的倒“U”型变为先下降后上升的“U”型趋势，且数值有所下降。纯技术效率和规模效率的均值走势未发生变化，但数值分别有所上升和下降。（2）从各市（州）看，武汉、黄石、十堰、宜昌、襄阳和荆门的综合效率、纯技术效率均出现明显上升，说明这些地区不仅外部环境好，而且管理水平也较高。而鄂州、孝感、荆州、黄冈、咸宁、随州、恩施、仙桃、潜江和天门的综合效率均出现下降，说明效率低水平并非单纯由环境因素造成，应该进一步加强自身创新实力，尤其是加大研发投入总量，调整企业规模，引进高端人才提升创新竞争力。考虑环境因素和随机噪声后，湖北省各市（州）的创新效率值有所变化，说明传统DEA方法倾向于高估或低估各市州的创新效率值，不能真实反映各个市州的创新效率水平。

规模报酬分析。16个市（州）在2013—2017年80个评测单元中，处于前沿面的有6个，均为规模报酬不变。非有效单元有74个，其目标值均为规模报酬递增。整体来看，规模报酬递增占比92.5%，规模报酬不变占比7.5%。武汉长期处于规模报酬不变的阶段，其他市（州）大部分年份均处于规模报酬递增。说明武汉经济发展水平较高，规模相对已经比较优化，而其他市（州）地区还处于规模不优的阶段。

市（州）差异分析。（1）从空间分布看，区域之间综合效率和規模效率差异明显，而纯技术效率比较接近，说明各市（州）之间的效率差异主要是由规模效率引起的。各市州创新综合效率从大到小依次为武汉、襄阳、鄂州、宜昌、黄石、孝感、十堰、荆州、荆门、黄冈、咸宁、随州、仙桃、潜江、恩施和天门。其中，武汉在三种效率评价中均名列前茅，天门则处于效率评价的末端;恩施、潜江、随州和咸宁的纯技术效率表现突出，但规模效率拉低了综合效率。（2）从时间趋势看，综合技术效率变化趋势大致可分为三类：第一种是稳定型，武汉的纯技术效率和规模效率连续五年均处于前沿面，决定其综合效率也处于前沿面;恩施、仙桃和天门长期稳定处于低位，这是因为规模效率也基本呈现长期稳定低位态势。第二种是上升型，如荆州、咸宁和潜江，这些城市主要是因为规模效率的上升。第三种是下降型，如黄石、十堰、宜昌、襄阳、鄂州、荆门、孝感、黄冈和随州。其中黄石、宜昌、孝感和随州等市是由于纯技术效率与规模效率均下降引起的，十堰、襄阳、荆门和黄冈主要是由于纯技术效率下降导致的，鄂州主要是由于规模效率的下降。

三、结论与建议

基于2013—2017年湖北省市级层面的数据，本文使用三阶段DEA模型对16个市（州）的城市创新效率进行了测算。研究发现：一是环境因素对创新效率产生显著影响。三阶段DEA剔除了环境因素，分离了管理无效率，在创新效率评价上更加准确。从调整前后结果比较来看，武汉、黄石、十堰、宜昌、襄阳和荆门的综合效率值出现明显的上升，而鄂州、孝感、荆州、黄冈、咸宁、随州、恩施、仙桃、潜江和天门的综合效率均出现下降，这说明有利的外部环境对效率有提升作用。二是创新效率和规模效率存在区域差异。从时间演变看，综合技术效率变化趋势存在区域差异，主要原因是各个市（州）的规模经济发展水平不同和各地的管理水平有所差异，其变化趋势大致分为稳定型、上升型和下降型。从空间分布看，武汉、宜昌、襄阳、鄂州、黄石的创新综合效率位于前列，而恩施、仙桃、潜江和天门等市则处于末端，这基本与现实经济状况相符。

应着眼于打造区域协同创新共同体，激活区域创新发展潜力，转变思维路径和发展模式，以湖北一圈（武汉城市圈）两群（宜荆荆和襄十随城市群）为载体，加强部门间、市（州）间协调联动，在一些重点领域和关键环节开展系统性、整体性、协同性改革先行先试。一是建立开放合作创新生态。整合知识、技术、资本、人才等创新资源，引导“一主两副”高水平创新区域与低水平区域的创新合作与交流，发挥国家级高新区溢出效应，引导高新区内主导产业的部分配套产业转移至周边腹地，支持其对区位相邻相近、产业关联同质的产业园区进行空间整合、资源整合和产业整合。推进区域人才柔性交流。加强人才政策衔接，探索专业技术职务聘任职业资格互认、毕业生实习创业互补流动、互派科技管理干部等人才流动新模式。省、市相互选派科技、商务、教育、卫生等领域优秀党政干部交流挂职和异地培训。依托企业创新平台，组织动员高校院所科技人才、创新团队跨区域到园区、企业挂职兼职。支持科技人才在企业、高校、科研院所之间流动或双向兼职。二是强化财政金融支撑功能。充分发挥政府资金对全社会研发经费投入的引导和拉动作用，加大对基础研究、产业技术联盟、科学仪器设备共享、国家级和省级创新平台、对外经贸合作区等财政经费投入。提高引导基金规模、出资比例及让利，引导民间资本参与。探索建立投融资服务平台，推动武汉股权托管交易中心提档升级。试行科技企业信用贷款及科技企业联投联贷联保机制。推广东湖高新区“投贷联动”模式和宜昌自贸片区“小微快贷”模式。建立创新券通存通兑试点，建立统一的创新券服务平台。

注释：

① 李婧：《考虑空间效应的区域创新效率测评》，《研究与发展管理》2011年第1期。

② 曹霞：《创新驱动视角下中国省域研发创新效率研究——基于投影寻踪和随机前沿的实证分析》，《科学学与科学技术管理》2015年第4期。

③ 时鹏将：《R&D投入产出效率的DEA分析》，《科学学与科学技术管理》2004年第1期。

④ 孙凯：《基于DEA的区域创新系统创新效率评价研究》，《科技管理研究》2008年第3期。

⑤ 冯志军：《我国区域科技创新二阶段效率评价及策略研究》，《科技进步与对策》2011年第6期。

⑥ 刘凤朝：《基于Malmquist指数法的我国科技创新效率评价》，《科学学研究》2007年第5期。

⑦ 徐小钦：《专利产业化示范项目扶持建设的重点产业选择——以重庆市为例》，《科技进步与对策》2008第9期。

⑧ 韩先锋：《我国区域科技创新效率、模式与收敛性分析》，《统计与决策》2010年第16期。

⑨ 刘明广：《区域创新系统的创新效率动态评价——基于省级面板数据的实证研究》，《科技管理研究》2015年第1期。

⑩ 李兰冰：《我国区域科技创新效率评價——以省际数据为样本》，《科技管理研究》2008年第9期。

{11} 陈伟：《中国区域创新系统创新效率的评价研究——基于链式关联网络DEA模型的新视角》，《情报杂志》2010年第12期。