电阻层析液固两相流传感器抗冲蚀磨损特性研究

李浩 李日新 周麒

摘 要：挖泥船浓度测量设备的有效性对施工效率提升具有很大促进作用，其测量精确性是实现智能挖泥的关键技术节点之一。电阻层析扫描成像技术为解决这一问题提供了方案，但传感器会受到冲蚀磨损影响使用寿命，也会造成安全隐患。本文以颗粒动力学为基础对传感器冲蚀磨损特性进行了CFD数值模拟，并和相关文献中的试验数据进行了对比。结果表明，在传感器内均存在最大磨损位置点，传感器材料的硬度值对最大磨损率影响较大，并呈现先增大后稳定的趋势。通过颗粒物与管道间碰撞过程来进行动量互换，颗粒物性、流速直接与最大磨损位置和数值相关联。壁面的最大剪切应力与颗粒物的物性相关，与管道材料及流速关联不大。

关键词：电阻层析成像技术;内衬技术;计算流体力学;冲蚀磨损;流动特性

中图分类号：U61            文献标识码：A            文章编号：1006—7973（2020）07-0054-04

1 前言

耙吸、绞吸、斗轮挖泥船施工是通过管道利用水力完成疏浚土的输送，浓度测量设备的有效性对施工效率的提升具有很大的促进作用，同时其测量的精确性是实现智能挖泥一个很关键的技术节点。挖泥船水力输送介质为液固两相流体，液体为海水或淡水，固体为疏浚土，包括淤泥、细粉沙、中粗砂、黏土、城市建筑垃圾、岩石、珊瑚礁等介质及其混合物。

目前，世界范围内挖泥船浓度的测量以核技术应用最为广泛，但其缺点亦非常明显：测量区域与整个横截面面积占比小、液固混合越不均匀测量精度越低、对体积产量的测量精度进行有效评估存在很大困难。鉴于以上问题，电阻层析扫描成像技术（ERT）为解决上述问题提供了一种解决方案。ERT技术是一种基于电阻传感器原理的层析成像技术，通过测量电阻率的分布来获得多相介质的分布。相对于核技术，ERT技术在测量液固两相流体时具有更大的测量面积占比、可实现更快速的测量、测量结果与真实浓度呈现线性关系、可实现可视化测量及测量图像数字化，直观观察管道内流态变化情况及流态图像的数字化，为智能判断与控制提供基础。

ERT技术应用于挖泥船施工需解决的关键问题之一，就是对传感器的抗磨损能力分析，此能力直接决定设备的使用寿命。据英国科学家T.S.Eyre[1]估计，冲蚀磨损导致的事故数占工程中磨损破坏总数的8%，且管道穿孔事故中有80%是由于磨损及冲刷腐蚀造成的。在2000年，中石化茂名炼油厂和齐鲁炼油厂[2]的管道事故中，发生了壁面减薄的现象。因此，研究传感器内冲蚀磨损机理，对增加传感器的使用寿命，提高检测效率有重要意义，有利于实际测试中的安全与高效，具有重要的实际作用。

影响传感器设备磨损的因素有很多，而研究磨损的学者们也根据这些因素提出了许多的磨损方程。磨损的影响因素主要有五种，即颗粒属性[3-4]，流体属性[5-7]，壁面材料[8-11]，颗粒冲击速度[12-13]和冲击角度。由于磨损预测涉及因素种类较多，可用不同的模型来表述这些因素的相互关系。在冲蚀磨损数值模拟中常用到四种模型：即用壁面反射模型[14-17]来模拟颗粒与壁面之间的交互作用;用湍流模型来模拟流体的运动;用三种耦合的方法来实现颗粒和流体间传质;以及用磨损模型来反映颗粒属性、流速、冲击角度等对磨损的影响。

虽然前人对ERT测量液固两相流浓度的系统组成、成像算法、测量精度等特性进行了大量的研究，得到了许多非常有价值的结论，但对ERT设备本身抗冲蚀磨损特性的研究依然不够全面。为了解决ERT测试过程中疏浚产物对ERT设备的冲蚀磨损，分析不同管材属性和颗粒物性下的冲蚀磨损特性，本文针对ERT技术中的实际工况对不同传感器材料、不同疏浚颗粒物物性及疏浚工程实际流速对传感器冲蚀磨损展开研究，得到最大磨损速率和壁面剪切力的规律，并基于此磨损规律提出合理的建议，在ERT选材和使用寿命评估方面具有指导意义。

2 数学模型

Navier-Stocks方程是流体的基本方程，该方程用来描述流体计算中的压力、速度和密度等相关信息的求解。在本文中，描述为连续方程和动量方程。湍流模型是用来计算连续相的模型，能较好地模拟管道中流体的流态。其中RNG k-ε 模型具有良好的稳定性和准确度，十分适合求解本文中的流态，选用该模型能得到较为精确的结果，在RNG模型中，为消除模型的影响，产生了一个求解不同湍流粘度的方程。

离散相方程是求解作用于离散相上的力来计算流体轨迹的。通过对作用于颗粒上的力进行积分，软件ANSYS Fluent 能够展示各个颗粒的轨迹，这个过程可以用拉格朗日方程來描述。     为虚拟质量因子，默认值为0.5。

流体通过阻力和湍流来影响离散相，颗粒的平均动量和平均湍流的减小反过来影响流体的流动，双向耦合用于解决这两个阶段之间的相互作用。当颗粒通过每个控制单元时，就会计算颗粒和流体间的动量交换。流体速度包括两个要素，即：平均速度和随机波动速度。随机波动速度影响粒子的运动轨迹。本文中，利用离散随机模型（DRW模型）来考虑颗粒-涡流的相互作用。波动速度服从高斯概率分布。双向湍流耦合使得由于颗粒阻尼和湍流涡流而引起的湍流量变化产生影响。为考虑这种影响， RNG k-ε模型方程应包含颗粒源相。

磨损模型用于模拟实际中管道壁面与颗粒间的碰撞产生磨损的大小，一个精确的模型得到的结果更加准确。而由于碰撞材料、流体等属性不同，许多研究学者都提出过冲蚀磨损模型，这些模型种类有很多，适应范围较窄，选择合适的磨损模型尤为重要。而Oka提出的模型与实验数据十分吻合。该模型如下所示

式中，E90是当冲击角为90°时的参考磨损率，V为颗粒物速度，Vref为参考速度，d为颗粒物粒径，dref为颗粒物参考粒径。Hv为材料的维氏硬度; n1和n2为常数;        为冲击角的无量纲函数;      为粒子入射角。

3 工况条件及仿真设置

几何模型为三段圆管道，中间为传感器管道，两端为疏浚管道。管道横截面直径为D=0.2m，传感器长度为2D，两端管道长度均为5D。横截面网格划分采用O网格。

本文的工况基于ERT设备在疏浚工程实际，选取的进口速度为4-6m/s，颗粒物为疏浚工程常见的物质，如表1。

湍流模型选择RNG k-epsilon模型。采用DPM模型和非稳态跟踪。内迭代步骤数为50步，时间步长为0.001s，时间步数为1000步。每个方程的控制单元残差小于10-4。液相的求解器类型为压力基，速度为绝对速度。入口边界条件设为“velocity-inlet”，壁面材料为密度为7800 kg/m3的壁面材料。粗糙度值设置为10μm，粗糙度常数设置为默认值是0.5。出口边界条件设为“pressure-outlet”。湍流强度设置为5%（完全湍流）。设水力直径与管径相同，为0.2 m。粒子是球形。颗粒密度不做强调时选值为1300 kg/m3。质量流量设定为0.023kg/s。壁面条件为“reflect”，出口是“escape”。“在所有情况下，颗粒均与流体以相同的速度射入管道。压力是1.01 × 105 Pa，温度设置为25℃。

4 讨论与分析

4.1模型验证

为验证本文选择的磨损模型，将验证模型的边界条件设置成与Ronald E [18]中的边界条件相同。验证模型的流速分别为15 m/s、23 m/s和27 m/s，流体的连续相为气体。固体颗粒为不规则的石英砂，密度为2650 kg/m3。表2的结果表明，仿真数据与实验数据基本一致，仿真结果符合要求。因此，验证模型与实验数据的差异在可接受范围内，该模型可以获得精确的磨损形状。

表2中得到的结果与实验值的差距较小，在允许的实验误差范围内。而且仿真得到的管道磨损形状与相关文献中的一致，这表明，这种构建得到的模型具有足够的准确性，能准确地模拟弯管内的磨损，得到具有实际意义的值，这为本文的计算结果提供了根本支持。

4.2 磨损特性

通过模拟得到的传感器段云图可以定性对其磨损特性分析，如图1。当维氏硬度为0.8GPa时，传感器受到磨损的位置较多且无规律性，最大磨损率为4.2×10-9Kg/m2/s。壁面有一段位置处于最大剪切应力区域，数值为0.114Pa。

4.3 传感器材料对冲蚀磨损率的影响

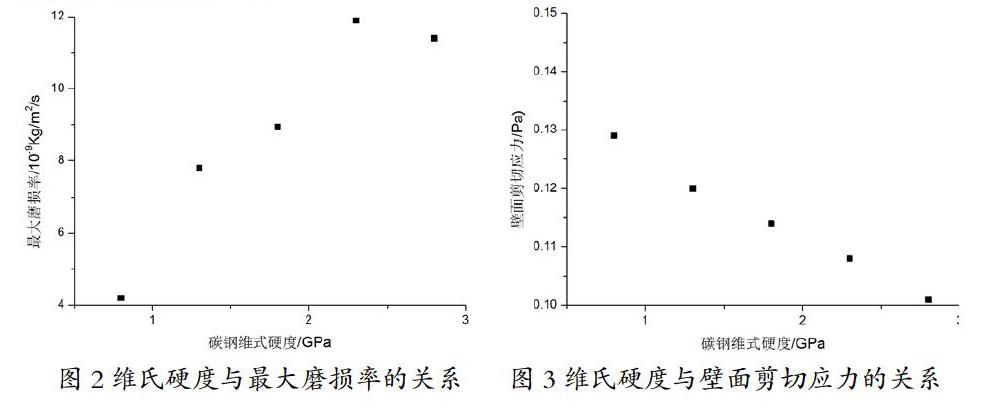
传感器在测试过程中存在磨损现象，它不仅与颗粒物的粒径、浓度、流速有关，还和传感器直径、材料等相关。将传感器内衬材料转化不同维氏硬度的材料进行分析，内衬设计对颗粒物与壁面碰撞起着缓冲作用。本文将其视为减小壁面材料硬度。保持进口速度为5m/s，进口颗粒为常见的淤泥。研究不同管道材料对管道磨损和强度的影响，如图2和图3。在仿真中，发现在改变维氏硬度时，最大磨损率均出现一处位置点。当维氏硬度为0.8-2.3GPa范围内，由于材料硬度不处在很高数值，随着硬度增大，管道壁面与颗粒物的碰撞愈发激烈，导致最大磨损率逐渐增大;当维氏硬度为2.8GPa时，此时硬度较大，颗粒物对管道的碰撞能力有效，使得最大磨损率略微减小。

随着硬度的变化，壁面最大剪切力基本趋于稳定，最大值与最小值相差0.03Pa，波动很小。这能说明硬度对壁面最大剪切力的影响特别小，在实际工程中可以忽略。

4.4 颗粒物物性对冲蚀磨损率的影响

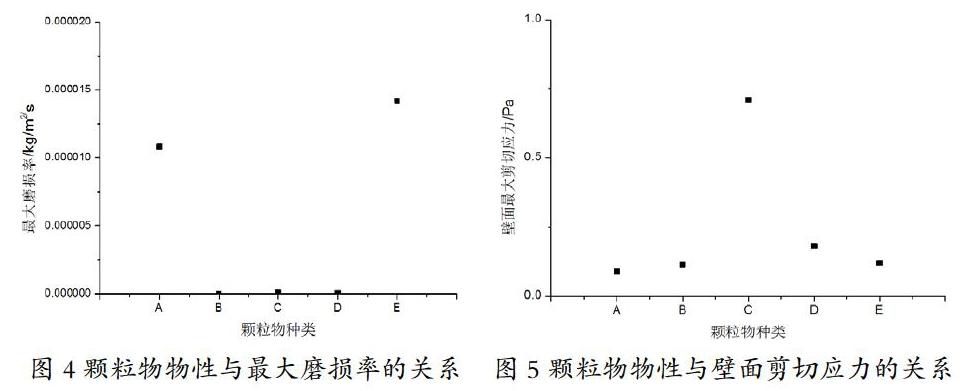
在维氏硬度为默认值1.8GPa，颗粒物进口速度5m/s的前提下，对不同颗粒物对最大磨损率和壁面强度进行了研究。首先值得注意的是，当颗粒物为城市建筑垃圾和细粉沙时，最大磨损率存在管道的两处位置点;其他的三种颗粒物对壁面只存有一处最大磨损位置。从图4可以看出，当颗粒物密度较大（颗粒物A、C、E）时，颗粒物对管道的磨损很严重，高达10-5Kg/m2/s数量级水平。当颗粒物密度较小（颗粒物B、D）时，颗粒物对管道的磨损在10-9Kg/m2/s数量级水平。同时，比较颗粒物A、C、E也发现，颗粒物密度对管道磨损的影响不大。由此得出，颗粒物的粒径对最大磨损率影响很显著，密度对最大磨损率影响很微弱。

对不同颗粒物对壁面最大剪切应力做了分析，如图5。当颗粒物为岩石时，壁面最大剪切应力值较大，这可能是因为岩石的密度和粒径值均较大，在它们的双重影响下，最大剪切应力也处于高位数值。

4.5 进口速度对冲蚀磨损率的影响

在保证颗粒粒径值默认为1×10-5m，颗粒物为淤泥，维氏硬度为默认值1.8GPa的工况下，对不同的颗粒物进口速度进行了分析。可以发现，当进口速度为4.5m/s时，最大磨损率存在于两个不同的位置点，在其他速度工况下，最大磨损率只存在于一个位置点。如图6，随着进口速度的增大，最大磨损率呈增大趋势再逐步稳定。这可能是因为，随着进口速度增大，颗粒物与壁面碰撞几率增多，所以最大磨损率逐渐变大;当进口速度增大到一定值后，壁面内颗粒物处于饱和状态，颗粒物与壁面碰撞几率波动不大，对壁面的影响能力趋于定值，故最大磨损率保持稳定。

随着进口速度的增大，壁面最大剪切应力处于很小幅度增大后稳定的变化趋势，如图7所示。随着进口速度的增大，颗粒物的动量也在不断增加，所以对壁面的剪切应力也在增强;当速度增大到一定值后，颗粒物与壁面接触区域有限，使得颗粒物与壁面动量交换有限，故剪切应力趋于稳定。但从剪切应力变化的数值来讲，随着进口速度的变化，壁面剪切应力的变化很微弱。

4.6 传感器内衬技术的应用

结合工程应用需求及数值模拟结果，提出两种内衬解决方案：①针对小型挖泥船，施工介质以淤泥、細粉沙为主的工况条件，传感器内衬采用聚氨酯内衬，降低设备采购成本;②针对中、大型挖泥船，施工介质涉及中粗砂、卵石、碎石、岩石、珊瑚礁、黏土等工况条件，传感器内衬采用复合耐磨陶瓷内衬，降低设备使用成本;自实船应用以来，取得优异的使用效果，历经各种复杂工况条件的考验，包括岩石、珊瑚礁、城市建筑垃圾、卵石等，如图8和图9。

5 結论

（1）对于ERT设备内两相流问题，使用DPM和RNG k-epsilon模型能够很好地模拟内部流动状态。模拟值与实测值表现出良好的一致性。

（2）在低位区间改变碳钢材料的硬度对最大磨损率影响较大，在高位区间硬度对最大磨损率影响不明显;管道中的最大磨损率对颗粒物的密度和粒径很敏感。在低位区间的进口速度对最大磨损率的影响也较为明显。管道与颗粒物之间通过碰撞来进行动量交换出现磨损点，进而产生最大磨损率位置点。碳钢材料、颗粒物物性及进口速度中壁面最大剪切应力影响较为明显的只有颗粒物物性。

（3）特有的内衬设计对磨损起到缓冲作用，模拟结果表明，内衬技术能有效地减小传感器最大磨损率，确保设备的使用寿命。

参考文献

[1] 牟军，张丰，肖延龄，等. 系统方法在冲蚀研究建模中的应用[J]. 材料导报， 1995， （01）： 4-8.

[2] 宋光雄，张晓庆，常彦衍，等. 压力设备腐蚀失效案例统计分析[J]. 材料工程， 2004， （02）： 6-9.

[3] Hutchings. Some comments on the theoretical treatment of erosive particle impacts[J]. Proceeding of the 5th International Conference on Erosion by Liquid and Solid Impact， 1980.

[4] Kevin Raymond Ahlert. Effects of Particle Impingement Angle and Surface Wetting on Solid Particle Erosion of AISI 1018 Steel[J]. 1994.

[5] Y. Zhang，E. P. Reuterfors，B. S. McLaury，et al. Comparison of computed and measured particle velocities and erosion in water and air flows[J]. Wear， 2007， 263： 330-338.

[6] Nan Lin，Huiqing Lan，Yugong Xu，et al. Effect of the gas–solid two-phase flow velocity on elbow erosion[J]. Journal of Natural Gas Science and Engineering， 2015， 26： 581-586.

[7] Kai Wang，Xiufeng Li，Yueshe Wang，et al. Numerical investigation of the erosion behavior in elbows of petroleum pipelines[J]. Powder Technology， 2017， 314： 490-499.

[8] Finnie. Erosion of metal by solid particles[J]. J. Mater， 1967， 2： 682-700.

[9] A. Levy，G. Hickey， Surface degradation of metals in simulated synthetic fuels plant environments[C]. International Corrosion Forum， 1982.

[10] Wenshan Peng，Xuewen Cao. Numerical simulation of solid particle erosion in pipe bends for liquid-solid flow[J]. Powder Technology， 2016， 294： 266-279.

[11] Wenshan Peng，Xuewen Cao. Analysis on Erosion of Pipe Bends Induced by Liquid-solid Two-phase Flow[J]. Journal of Chinese Society of Corrosion and Protection， 2015， 35（6）： 556-562.

[12] Ronald E. Vieira，Netaji R. Kesana，Brenton S. McLaury，et al. Experimental investigation of the effect of 90 degrees standard elbow on horizontal gas-liquid stratified and annular flow characteristics using dual wire-mesh sensors[J]. Experimental Thermal and Fluid Science， 2014， 59： 72-87.

[13] Carlos Antonio Ribeiro Duarte，Francisco Jose de Souza，Vinicius Fagundes dos Santos. Numerical investigation of mass loading effects on elbow erosion[J]. Powder Technology， 2015， 283： 593-606.

[14] D. W. Stanton，C. J. Rutland. Modeling Fuel Film Formation and Wall Interaction in Diesel Engines[J]. SAE Paper， 1996， 960628.

[15] P. J. ORourke，A. A. Amsden. A Spray/Wall Interaction Submodel for the KIVA-3 Wall Film Model[J]. SAE Paper 2000， 2000-01-0271.

[16] G. Grant，W. Tabakoff. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles[J]. Journal of Aircraft， 2012， 12（5）： 471-478.

[17] M. Sommerfeld. Modelling of particle-wall collisions in confined gas-particle flows[J]. International Journal of Multiphase Flow， 1992， 18（6）： 905-926.

[18] Ronald E. Vieira，Amir Mansouri，Brenton S. McLaury，et al. Experimental and computational study of erosion in elbows due to sand particles in air flow[J]. Powder Technology， 2016， 288： 339-353.