仪器噪声在近红外光谱偏最小二乘模型内的传播效应
2020-11-06张若秋杜一平
张若秋,杜一平
(华东理工大学 上海市功能性材料化学重点实验室 化学与分子工程学院,上海 200237)
近红外(Near-infrared,NIR)光谱分析是近年来最引人关注的分析技术之一,在农业、制药、化工等众多领域得到广泛应用[1-2]。目前NIR技术的发展重点是应用,简便、快速、无损、准确等优点正是其受重视并被广泛应用于国民经济发展各个领域的本质原因。但在使用NIR技术的基层单位,技术队伍的研究能力往往不如研发单位,更不及高校和专门的科研机构。而NIR技术使用和推广的难点是近红外光谱分析模型的建立需要一些专门的技术,尤其是依赖于化学计量学。因此,模型的建立和维护是近红外光谱技术发展的一个突出难点和瓶颈。
偏最小二乘(Partial least squares,PLS)是近红外光谱多元校正领域使用最为广泛的算法之一[3-4]。在光谱多元校正的实际应用中,有很多因素会影响该算法的建模过程和模型的预测能力,其中包括光谱仪器噪声。然而,目前绝大多数研究都针对如何使用滤波器或平滑算法减少光谱噪声[5-6],鲜有针对仪器噪声如何影响偏最小二乘建模过程及其预测能力的研究。本文重点阐述和讨论仪器噪声怎样通过第一个隐变量的计算被引入模型中,并随着后续隐变量不断在模型中传递和累积从而对整个建模过程产生影响,可为今后进一步研究在建模中减少或抑制噪声在模型内的传播和放大提供理论依据。
1 仪器噪声对偏最小二乘建模的影响
样本的测量光谱用X表示,组分含量用y表示,多元校正关系模型为y=Xβ+e。考虑测量光谱存在误差,将X表示为:
X=X0+E
(1)
其中,X0为不含测量误差的真光谱,E表示仪器噪声,假设矩阵中的每个元素均满足均值为0且方差相同的高斯分布。类似地,含量真值用y0表示(本文只考虑光谱存在误差,含量无误差,即y0=y)。
1.1 偏最小二乘算法实现
PLS的主流实现方式有非线性迭代偏最小二乘(NIPALS)[7]和SIMPLS两种,为方便理论推导本文使用SIMPLS,下文给出SIMPLS的伪代码[8]。SIMPLS算法流程如下:
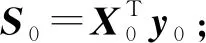
Fora=1,…,A;
a=1:对S0进行奇异值分解;
a>1:对(I-P(PTP)-1PT)S0进行奇异值分解;
计算得到权重向量r=第一个左奇异向量;
计算得到得分向量t=X0r;
将r、t和p分别存入R、T和P;
End
无噪光谱矩阵X0含有p个变量和n个样本,浓度向量y0含有n个样本。R、T和P分别代表权重矩阵、得分矩阵和载荷矩阵,而βpls则为偏最小二乘模型的回归系数向量。为方便,本文使用LSV1(S0)表示S0的第一个左奇异向量。
1.2 仪器噪声传递
当PLS模型的隐变量数量(nLVs)为k个时,在不同隐变量下所形成的空间和由Krylov序列形成的空间满足如下等式[5]:
{Rk}={S0,XTXS0,(XTX)2S0,…,(XTX)k-1S0}
(2)
{Pk}={XTXS0,(XTX)2S0,…,(XTX)kS0}
(3)
以上两个等式表明协方差矩阵S0(当预测指标只有1个时是协方差向量)和XTX完全确定了βpls。前者确定模型的初始方向,而后者则影响每个隐变量的实际计算。当光谱数据中包含了仪器噪声时,S0和pk的计算可改写为如下形式:
(4)
(5)
因此,通过上述公式发现偏最小二乘模型将从第一个隐变量开始发生偏离真模型的现象,噪声同时被引入到模型中,并在随后隐变量的计算过程中被不断传递和累积:
(6)
Rk=[LSV1(S1),LSV1(S2),…,LSV1(Sk)]
(7)
βpls=RkRkTS0
(8)
上述噪声传递过程同时也会对偏最小二乘模型的预测能力产生影响。预测残差可表示为:
(9)
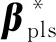
(10)
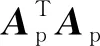
(11)
(12)
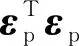
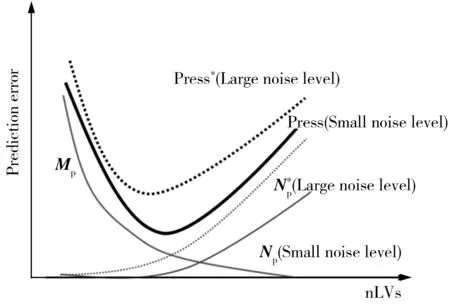
图1 噪声传递和偏最小二乘预测误差关系示意图Fig.1 The scheme of the relationship between noise propagation and prediction error
噪声传递和偏最小二乘的预测误差关系如图1所示,不同噪声水平下的最优隐变量数也将发生改变,噪声水平越高,最优隐变量的数值越小。这说明噪声传递不仅影响偏最小二乘模型的预测能力,还会给模型的选择带来影响。
2 数据集与计算方法
2.1 数据集模拟
本文用模拟数据对上述讨论进行验证。模拟数据集包含了2 000个建模样本和2 000个独立预测样本,其变量数为1 000。数据集中包含1个待测组分和40个干扰组分,共41个组分。每个模拟组分的纯光谱信号均满足一个随机均值和方差的高斯分布。建模集中待测组分和干扰组分的浓度值服从0到1的均匀分布,而在预测集中服从0.05到0.95的均匀分布。模拟光谱由浓度矩阵和纯光谱信号矩阵相乘得到。
对于每个固定的光谱信号xi(i=1,2,…,n)均产生一个服从标准高斯分布的噪声向量ei,噪声水平的大小定义为ei的最大值和xi的比值。更高的噪声水平意味着更低的信噪比(S/N),反之亦然。3个不同水平的噪声(0.3%、0.75%和1%)用于给无噪光谱数据添加人为噪声。
2.2 指标与计算软件评价
评价所建立的NIR模型通常考虑模型误差和相关系数两个指标,本文只考虑模型误差指标。建模时一般将数据集划分为校正集(C)、交互检验集(CV)和预测集(P),因此模型误差也包括校正误差、交互检验误差和预测误差。模型误差用均方根误差(Root mean squared error,RMSE)表示:
(13)
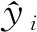
已有不少研究表明蒙特-卡洛采样(Monte-carlo sampling,MCS)能够降低模型过拟合的风险[9-10],因此本文采用基于MCS的方法,即采样误差分布分析的交互检验(Cross-validation based on sampling error profile analysis,SEPA-CV)[11]确定偏最小二乘的最优隐变量大小。MCS的采样数和建模样本比例分别设定为2 000和0.8。所有计算均使用MATLAB完成(Version 2010a,The MathWorks,USA)。
为准确量化偏最小二乘模型的噪声水平,采用Durbin-Watson(DW)[12-16]统计量评价噪声对模型的影响程度。DW统计量由下式计算得到:
(14)
xi和xi-1是p维向量中的两个连续元素。如果整个向量中连续元素间的相关性很弱,例如该向量中每个元素均为随机变量,则DW统计量的大小将收敛于2。一个拥有至少100个元素的随机向量的DW统计量的95%置信区间在1.7和2.3之间。
3 结果与讨论
3.1 噪声传递对偏最小二乘模型回归向量的影响
首先使用DW统计量对3种不同噪声水平的光谱所建立的偏最小二乘模型的权重向量r、载荷向量p和回归系数向量βpls进行噪声程度的估计,其结果见图2。
由图2可知,偏最小二乘模型中这3种向量的DW统计量均随着隐变量数的增加而增加,这反映了噪声在偏最小二乘模型中的传递和累积现象,与“1.2”理论推导的结果相符合。对于无噪光谱所建立的PLS模型,在1~41个隐变量范围内,r、p和βpls的DW统计量远小于有噪光谱建模得到的各中间向量的DW值。r和p的DW统计量在第42个隐变量处突然增至2左右,说明此时这两个向量已无法包含任何有用的光谱信息,因为模拟数据集的真实组分数是41。然而βpls的DW在第42个隐变量处却增加不明显,这是因为βpls是由全部权重向量r的线性组合,其DW的大小应该由这些权重向量的噪声程度共同决定。对于包含了仪器噪声的光谱所建立的PLS模型来说,在前25个隐变量下r、p和βpls的DW与无噪光谱PLS模型相比其对应的向量DW相差不大,但在第25个隐变量之后它们的差异显著增加,这是因为噪声的传递和累积的显著程度会随着隐变量数的增加而增加。
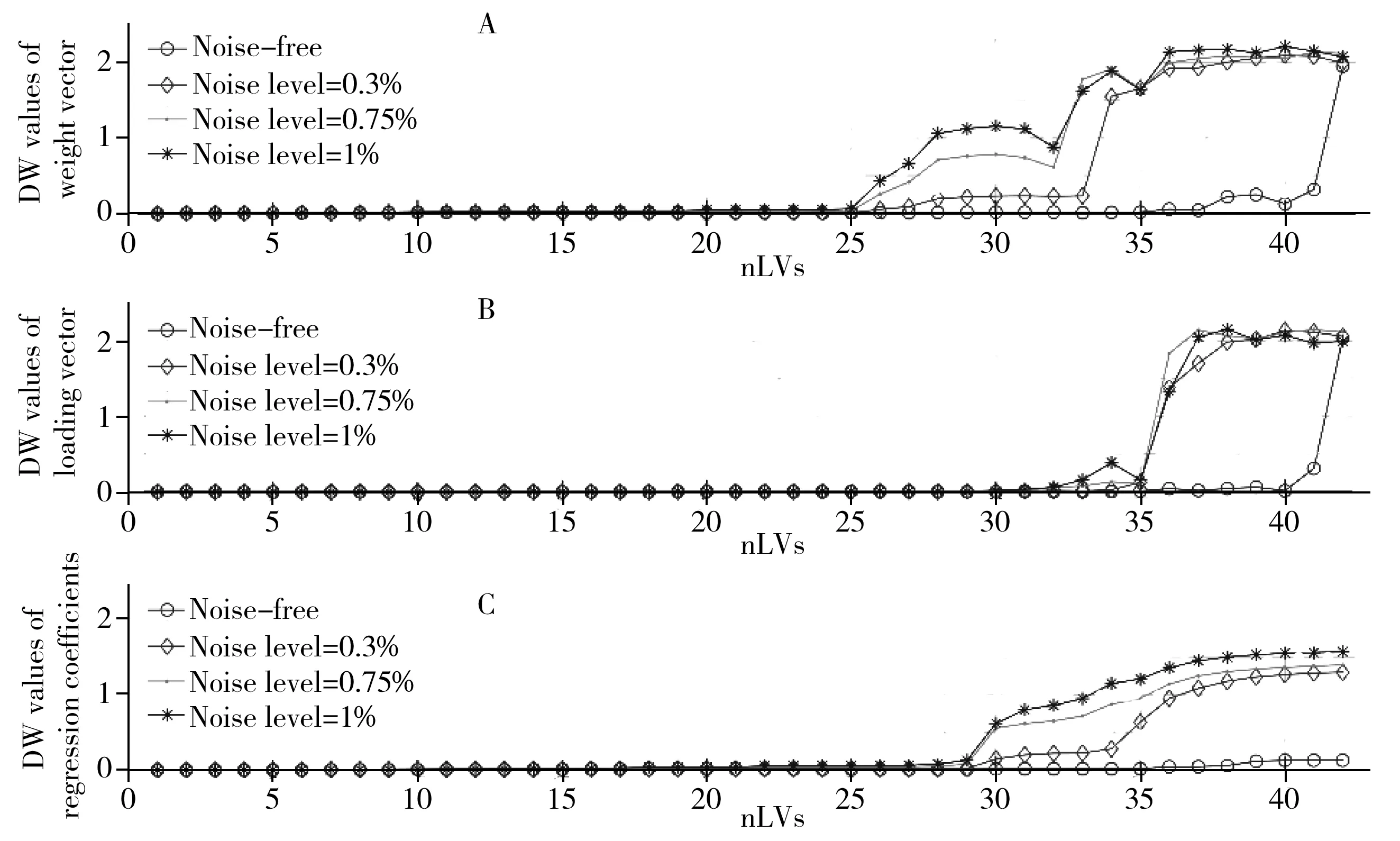
图2 模拟数据集在隐变量1~42下建立的偏最小二乘模型的r(A)、p(B)和βpls(C)的DW统计量Fig.2 DW values of r(A),p(B) and βpls(C) from simulated dataset with different noise levels at nLVs from 1 to 42
3.2 噪声传递对模型预测能力的影响
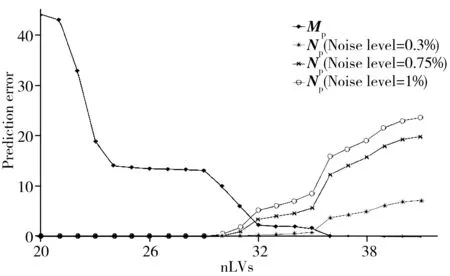
图3 模拟数据集中不同噪声水平光谱所建立 模型的预测误差示意图Fig.3 The prediction error of PLS models built by simulated dataset with different noise levels
采用上述模拟数据验证噪声传递对PLS模型预测能力的影响,结果见图3和表1。Mp为无噪光谱所建立的偏最小二乘模型的RSS,随着隐变量的增加,模型复杂度不断增加,Mp则不断降低,直至隐变量数量和模型的真实组分数(41)达到一致,此时模型的复杂度最优。使用无噪光谱建立的PLS模型的预测误差并不包含Np项,因为Np是由仪器噪声产生。由图3可知,Np的大小受两方面影响,一是其随着PLS隐变量数量的增加而增加,二是其随着噪声水平的增加而增加,这与“1.2”的理论分析一致。由图4和表1可知,Np的存在和增大会使模型的预测能力下降。

表1 模拟数据集的交互检验和RMSEP结果Table 1 Results of cross-validation and RMSEP to simulated dataset
图4和表1描述了模拟数据集交互检验和RMSEP的结果。对于无噪光谱建立的模型,最优隐变量数量和期望的情况一致(均为41),且在该隐变量下的RMSECV和RMSEP均很接近于0(1.190 2×10-6和2.774 5×10-6),此时该模型是这套模拟数据集的真实模型。随着光谱的噪声水平增加,模型的RMSECV和RMSEP相应增加,但更重要的是模型的最优隐变量也不断发生变化(例如:对于噪声程度为0.3%和1%的光谱来说,最优隐变量分别为33和31)。此外,不同噪声水平下所建立模型的RMSECV和RMSEP的差异随着隐变量的增加而增加,这证明了“1.2”的理论推导,即噪声会在PLS模型中不断传递和累积。由图4还能发现,无噪光谱建立的偏最小二乘模型的预测误差在隐变量超过41后会突然显著增加,这意味着模型的过拟合。
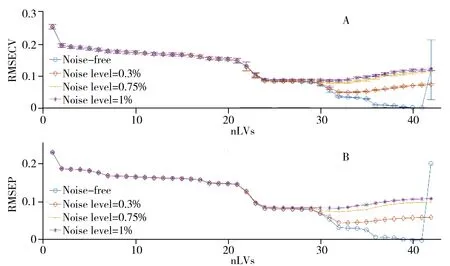
图4 模拟数据集包含不同水平噪声的光谱所建立模型的RMSECV(A)和RMSEP(B)Fig.4 RMSECV(A) and RMSEP(B) values at nLVs from 1 to 42 for simulated dataset

图5 第一个隐变量下PLS和PoLiSh模型的回归系数 及二者差值Fig.5 Regression coefficients of PLS and PoLiSh and their differences
3.3 去噪算法对噪声传递的验证
采用PoLiSh算法对人为添加1%噪声的模拟数据进行噪声传递的验证。PoLiSh算法的原理为,在使用NIPALS计算每一个隐变量下权重向量时,对其使用Savizky-Golay平滑[17]以消除噪声的积累。本文中Savizky-Golay平滑窗口大小为21,拟合阶数为2,使用PoLiSh所建立模型的最优隐变量数为35,相应RMSEP值为0.076 0。与表1中引入了1%噪声的光谱所建立的PLS模型相比,RMSEP降低且最优隐变量的数目增加,说明PoLiSh一定程度上减少了噪声的影响。图5反映了第一个隐变量的部分PLS模型和PoLiSh模型,可以明显看出使用包含仪器噪声的光谱建立的PLS模型从第一个隐变量开始包含噪声,而PoLiSh算法建立的模型可在一定程度上减弱噪声的影响。
4 结 论
本文阐述了仪器噪声如何从第一个隐变量的计算开始被引入偏最小二乘模型中并通过随后的隐变量计算被不断传递和累积,通过对偏最小二乘的计算过程相关公式的推导和对一套模拟光谱数据集的详细研究,总结并论证了与无噪的光谱相比,噪声的引入将使得偏最小二乘模型的预测能力变差且模型最优隐变量数减少,且光谱中包含的噪声水平越高,则其对模型预测能力和最优隐变量的改变越大的结论。
