基于尺度不变特征变换筛选稳定特征波长的近红外光谱模型传递方法
2020-11-06洪士军张立国倪力军栾绍嵘
洪士军,黄 雯,张立国,葛 炯*,倪力军*,栾绍嵘
(1.华东理工大学 化学与分子工程学院,上海 200237;2.上海烟草集团有限责任公司 技术中心理化实验室,上海 200082)
近红外光谱(Near infrared spectra,NIRS)是一种简单、快速的新型分析方法[1]。20世纪80年代后期以来,随着NIRS仪器的不断改进、化学计量学方法的应用和计算机的快速发展,NIRS技术被广泛应用于各个领域[2]。建立一个良好的NIRS模型需要足够多的样品数据并进行方法和模型参数优化,模型建立、维护需要人力、物力的持续投入,通常希望所建立的NIRS模型可以在不同仪器之间共享[3]。但由于各仪器的使用环境、寿命及状态不同,相同测试条件下,同一样品在同型号的不同仪器上的光谱响应并非完全相同,导致主仪器上所建立的NIRS模型对从仪器样品的预测误差可能超出许可范围,此时需要采用各种模型传递方法对从仪器光谱或主机模型进行修正[4]。本课题组提出的根据仪器间光谱差异的方差分析[5-6]、光谱比值分析[7]筛选仪器间信号一致且稳定的波长,基于这些波长的光谱信息在主机建立偏最小二乘(PLS)近红外光谱模型,并直接用于从机玉米、黄芩样品中主要成分含量预测的方法,对从机样品的预测误差与分段直接校正算法(Piecewise direct standardization,PDS)相当或更低。进一步在一致且稳定波长的基础上,综合应用相关系数、无信息变量消除(Uninformative variable elimination,UVE)[8]等波长筛选方法优化波长组合后建立烟叶总植物碱NIRS模型,该模型直接预测从机烟叶样品总植物碱的误差满足企业内控要求[9]。文献[10]通过分析主、从机光谱在不同波长下的相关性,筛选仪器间光谱响应一致性好的波长,建立了玉米中主要成分含量的NIRS模型,对从机样品的预测误差与主机相当。上述研究表明基于仪器间光谱响应一致性好的波长建立NIRS模型,有助于提高模型的稳健性,使模型可在不同仪器间直接共享,而无需在模型传递过程进行从机光谱校正或模型校正,比传统的有标样模型传递方法简便。但上述文献报道的波长筛选过程仍需若干主、从机样品光谱作为波长筛选的信息来源,不能称之为完全意义的无标样模型传递。
尺度不变特征变换(Scale invariant features transform,SIFT)算法是一种用来提取图像局部性特征的算法,该方法可在不同尺度空间查找图像中一些与其周围区域有高区分度的局部图像特征,这些特征(又称关键点)具有重复性好、区分度和准确度高的特点,并且在不同尺度空间保持不变,不随图像旋转、亮度变化而改变,对视角变化、仿射变换、噪声也保持一定程度的稳定性。通过提取这些特征的位置、尺度、旋转不变量,可实现对图像的精准识别[11-12]。本文以烟叶总植物碱近红外光谱模型的建立和转移为背景,利用SIFT算法提取主机样品一维近红外光谱在不同尺度下的关键点,这些点即为主、从机光谱中的稳定特征波长。以这些波长的光谱信息建立近红外光谱模型,可剔除噪声和无效信息对模型的干扰,获得稳健的近红外光谱模型,有望实现模型在不同仪器间的共享或直接转移。
1 算法与原理
1.1 一维SIFT算法筛选稳定特征波长
一维SIFT算法是二维SIFT算法的特例,其核心是构建不同尺度空间,寻找在不同尺度下均保持稳定不变的关键点。主要步骤如下:
(1)构建尺度空间
尺度空间包含两个尺度概念,一个尺度是对光谱图像的采样间隔,不同采样间隔构成了图像抽提的尺度;另一个尺度是对光谱信号进行不同尺度变换的尺度。高斯卷积核是实现尺度变换的唯一线性核,一幅一维光谱图像在不同尺度下的变换由光谱与高斯卷积核卷积获得:
L(x,σ)=G(x,σ)*I(x)
(1)
上式中I(x)为近红外光谱数据,x(光谱波长)是空间坐标,x坐标的间隔构成不同尺度空间的光谱I(x)。G(x,σ)是尺度可变高斯函数,又称为高斯卷积核,其定义如下:
(2)
σ为尺度空间变换因子,是高斯正态分布的方差,其大小决定图像的平滑尺度。大的σ对应粗糙尺度(低分辨率)图像的概貌特征,小的σ对应精细尺度(高分辨率)图像的细节特征。图1为二维、一维图像在不同空间尺度(采样间隔)和不同尺度变换因子σ下得到的高斯卷积示意图。由该图可知,对于二维图像,随着采样步长(x的间隔)的增大,尺度空间L(x,σ)变小,不同尺度空间L(x,σ)构成金字塔形状,称为高斯金字塔。对于一维图像,高斯金字塔退化为一个三角形。每个尺度空间L(x,σ)由若干长度相同的层构成不同组Octave1、Octave2…,采样间隔(x的间隔)不同产生长度不同的组,高斯卷积的尺度变换因子σ大小不同产生同组中的不同层。高斯金字塔的组数O、每组层数S及尺度变换因子σ决定了高斯金字塔的结构。
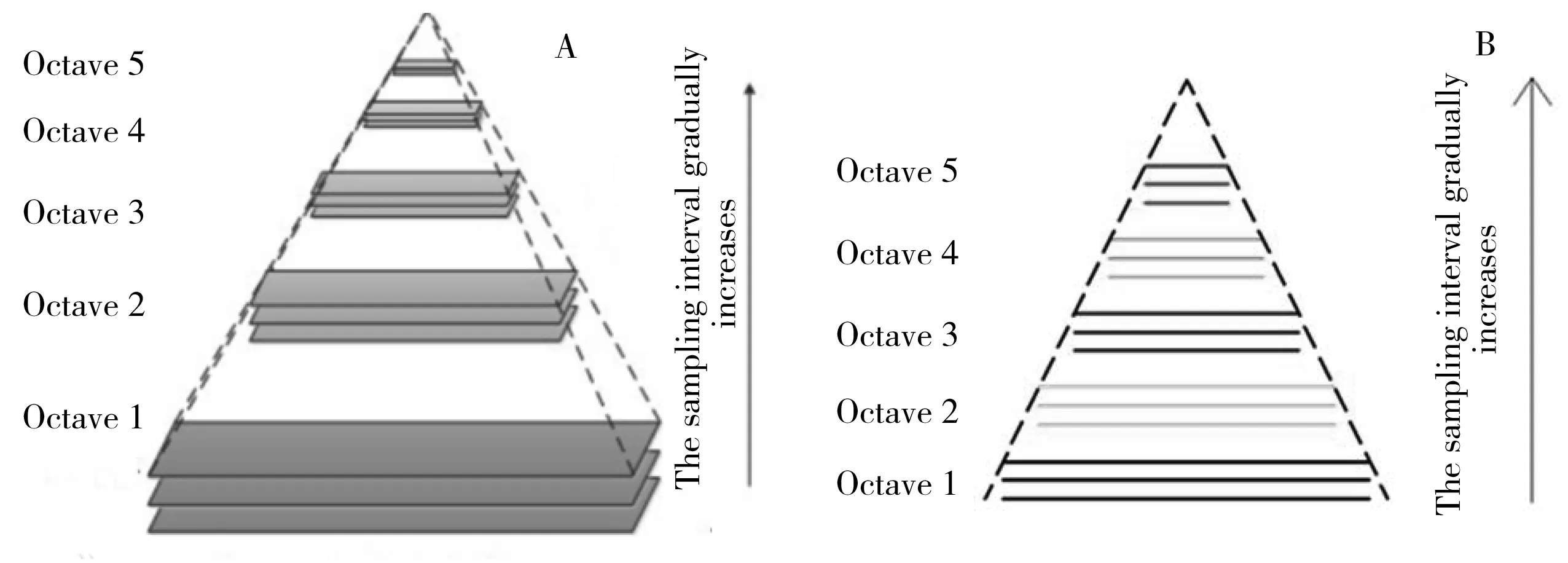
图1 二维图像(A)以及一维图像(B)的高斯金字塔示意图Fig.1 Schematic diagram of Gaussian pyramid of two-dimensional image(A) and one-dimensional image(B)
(2)进行尺度空间极值检测
搜索所有尺度上的光谱点,通过高斯差分(DOG)尺度空间来识别潜在的对尺度和旋转不变的关键点。DOG尺度空间由不同尺度的高斯差分核与光谱图像卷积生成:
D(x,σ)=(G(x,kσ)-G(x,σ))*I(x)=L(x,kσ)-L(x,σ)
(3)
式(3)中k为相邻层之间尺度因子大小的比例。第一组第一层的σ称为初始σ,记为σ0。
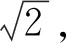
(3)高斯金字塔结构参数的优化
采用一维SIFT算法可根据一根光谱确定在光谱特定金字塔结构下的关键点集合。基于同一个样品连续p次测量的精密度光谱数据,可得到p个关键点集合。由于仪器噪声和测试误差等因素影响,同一样品连续p次测试的光谱不可能完全重合。因此,这p个集合中的关键波长点也不完全重合。本文以重现率(Percent recurrence,PR)和重现度(Reproducibility,RPD)衡量SIFT算法筛选出的波长的稳定性,以PR和RPD最大为目标,采用3因素3水平正交表优化高斯金字塔的结构参数。SIFT筛选波长重现率和重现度的计算公式如下:
PR=(n0×w0+n1×w1+n2×w2)/n
(4)
RPD=(n0×w0+n1×w1+n2×w2)/p
(5)
n0代表p次筛选出来的波长点相同的波长个数,n1代表p次筛选出来的波长相差一个点数的波长个数,n2代表p次筛选出来的波长差异在两个点数的波长个数,n代表根据p条精密度测试光谱筛选出的波长总数。w0、w1和w2分别为波长点重合度不同情况下的权重因子,对于p次全部重合的波长,其个数n0所乘的权重因子w0应该最大,本文设w0为3;基于该原则,对于波长相差一个点的波长个数n1,其所乘的权重因子w1定义为2,波长相差2个点的波长个数n2所乘的权重因子w2设为1。
1.2 近红外光谱模型的建立与评价
以所筛选的稳定特征波长下的光谱信息为自变量,采用偏最小二乘(PLS)算法建立待测性质的定量模型。以RMSEC(校正集的均方根残差)评价模型的拟合性能,RMSEP(验证集的均方根残差)和MRE(相对误差绝对值的平均值)来评估模型的预测性能及传递性能。
(6)
(7)
式(6)~(7)中的yi,actual为第i个样品实测值,yi,predicted为第i个样品的模型预测值,m为样品数目,RMSEP与RMSEC计算公式相同,但在计算时将公式(6)中校正集样本替换成预测集或验证集样本。RMSEC越小,则认为模型的拟合性能越好;RMSEP及MRE越接近于0,则认为模型的预测性能越好。烟草企业内控指标要求烟叶总植物碱的MRE小于6%。
本文所有算法在MATLAB平台完成和编译。
2 实验部分
本文共使用3套烟叶样本数据集,Set A由78个烟叶样本分别在4台AntarisⅡ近红外仪器(赛默飞世尔科技有限公司)上测得的光谱组成,4台仪器分别为主机M(Master)、3台从机S1(Slave 1)、S2(Slave 2)和S3(Slave 3);Set B由279个在主机M上测得的烟叶样本光谱组成。Set A、Set B中各烟叶样品的总植物碱采用YC/T 160-2002[14]测定,其含量在0.55%~6.30%之间。某一烟叶样品在主机M上连续测量3次的精密度近红外光谱记为Set C。
烟叶经烘箱50 ℃烘干后粉碎,过40~60 目筛。置于可旋转石英杯中,在(22±4)℃、30%~80%湿度下测试其光谱:分辨率取8 cm-1,波数范围取4 000~10 000 cm-1,扫描64次,增益取2。
3 结果与讨论
3.1 SIFT算法中的参数优化
取组数O的水平为3、4、5,层数S的水平为5、6、7,尺度因子σ0水平取1.5、2.5、3.5。以Set C中的3次精密度测试光谱为信息来源,基于正交表L9(33)筛选出的3个波长集合的重现率与重现度如表1所示。
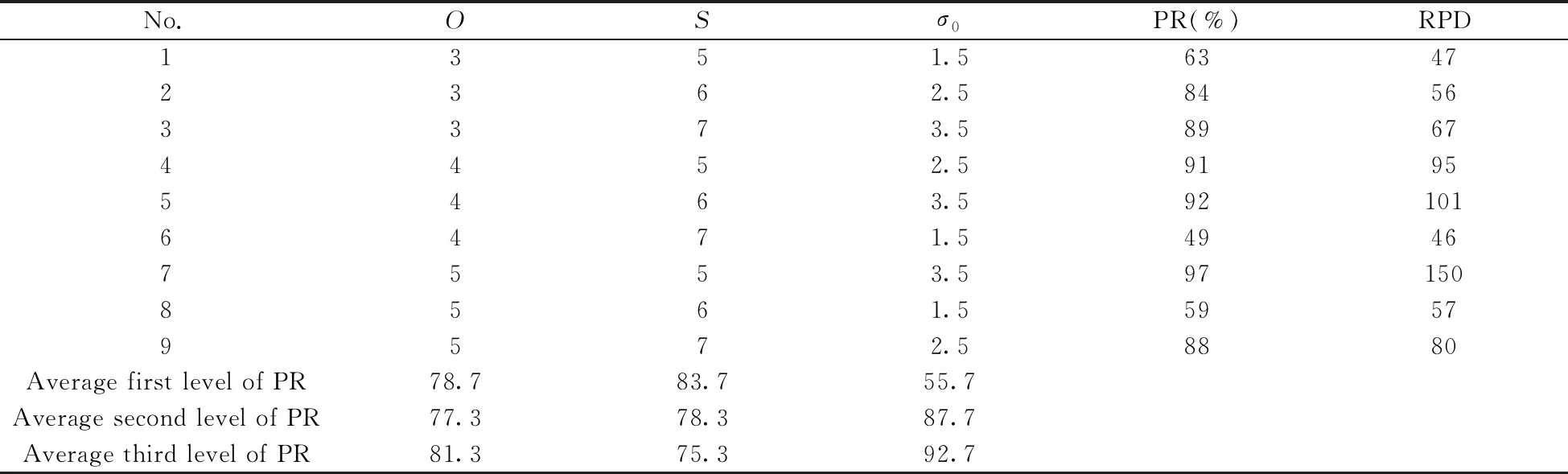
表1 根据正交表L9(33)筛选出的波长重现率及重现度Table 1 Wavelength reproducibility rate and reproducibility based on orthogonalTable L9(33)
由表1可知,重现度RPD与重现率PR呈正相关趋势,故只对重现率PR进行方差分析,结果如表2所示。

表2 表1中重现率的方差分析结果Table 2 Variance analysis results of reproducibility rate inTable 1
由表2可知,组数和层数的P值远大于0.05,说明组数O和层数S的取值对重现率、重现度与结果无显著影响。而高斯卷积初始尺度因子σ0的P值远小于0.05,表明σ0值的变化对波长筛选结果有显著影响。由表1可知,组数O的最优水平为5,层数S的最优水平为5,σ0的最优水平为3.5,最优的各因素水平组合为第7号实验,对应的波长重现率为97%。
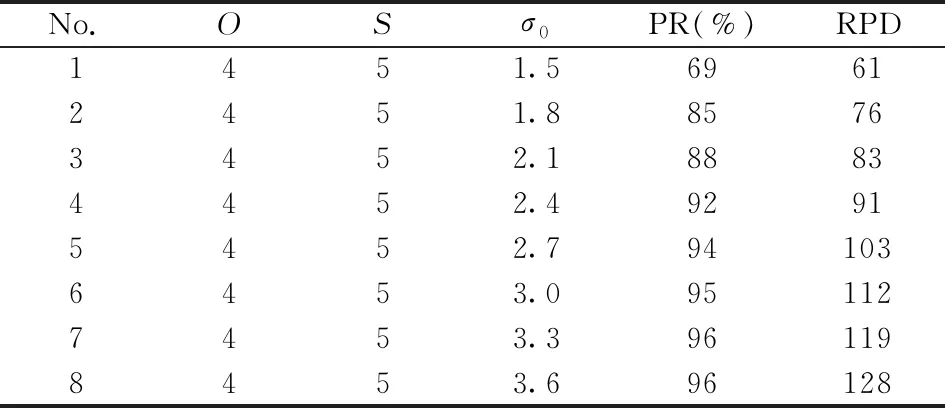
表3 O=4,S=5时,不同σ0下SIFT方法所 筛选波长的重现率与重现度Table 3 Reproducibility rate and reproducibility of wavelengths selected by SIFT with different σ0 when O=4,S=5
由于组数和层数的影响不显著,为减少运算量,将高斯组数设为4,层数设为5,探索σ0不同取值下的重现率变化情况,如表3所示。
由表3可知,σ0取2.7时重现率可以达到94%,σ0的继续增大对于重现率的提升贡献有限,而重现度随着σ0的增大有较为明显的提升。根据式(7)可知,重现度反映的是根据3次精密度测试光谱筛选出的稳定特征波长重合的波长个数的均值,其随σ0增大而增大。根据本课题组前期研究[9],在筛选的波长个数为80~120范围内,基于这些波长所建烟叶总植物碱NIRS模型的MRE在5%左右,满足企业内控要求。σ0取2.7时,可筛选出103个波长。故本文取高斯金字塔组数为4,层数为5,初始σ0取2.7。
3.2 烟叶样品光谱及SIFT方法所筛选的稳定特征波长
采用Set B数据建立主机模型,以Set A中主机M上测试的78个烟叶样品为主机外部验证集,Set A中分别在S1、S2、S3上测试的78个样品为从机检验集。首先将所有的光谱数据经过标准正态变换(SNV)+一阶导数预处理,再从Set B的279个建模样品中利用基于x-y空间距离划分样本的SPXY(Sample set partitioning based on jointx-ydistance)方法[15]分别挑选差异最大的前5、10、15、20、30个代表性样品。采用“3.1”得到的SIFT方法中的优化参数,根据这5(10、15、20、30)个代表性样品的近红外光谱分别筛选得到5(10、15、20、30)个稳定特征波长集合,每个集合的波长点数在80~90之间。取这些集合的交集,仅能得到40个左右的波长点,以这几十个波长的光谱信息建立烟叶总植物碱NIRS模型时,由于模型可调参数太少,其MRE超过6%,不满足企业内控要求。故本文分别取这5(10、15、20、30)个波长集合的并集作为SIFT算法筛选的稳定特征波长点,以此建立的烟叶总植物碱NIRS模型记为SIFT-PLS模型。除根据5个样品光谱筛选的波长所建立的SIFT-PLS模型不能保证对3台从机样品总植物碱的MRE小于6%之外,取10、15、20及30个样品光谱筛选波长所建的SIFT-PLS模型预测主、从机样品总植物碱的MRE均小于6%。限于篇幅,本文只给出10个代表性样品光谱所筛选的波长集合并集的结果,最终得到304个稳定特征波长点。筛选出的波长及由这些波长绘制的4台近红外仪器的平均光谱如图2B所示。由该图可见,根据这304个特征波长点的光谱响应所绘的图虽然不是很光滑,但保留了原样品光谱(图2A)的基本图像特征,说明SIFT方法筛选的波长确实提取出了烟叶样品的主要光谱特征。
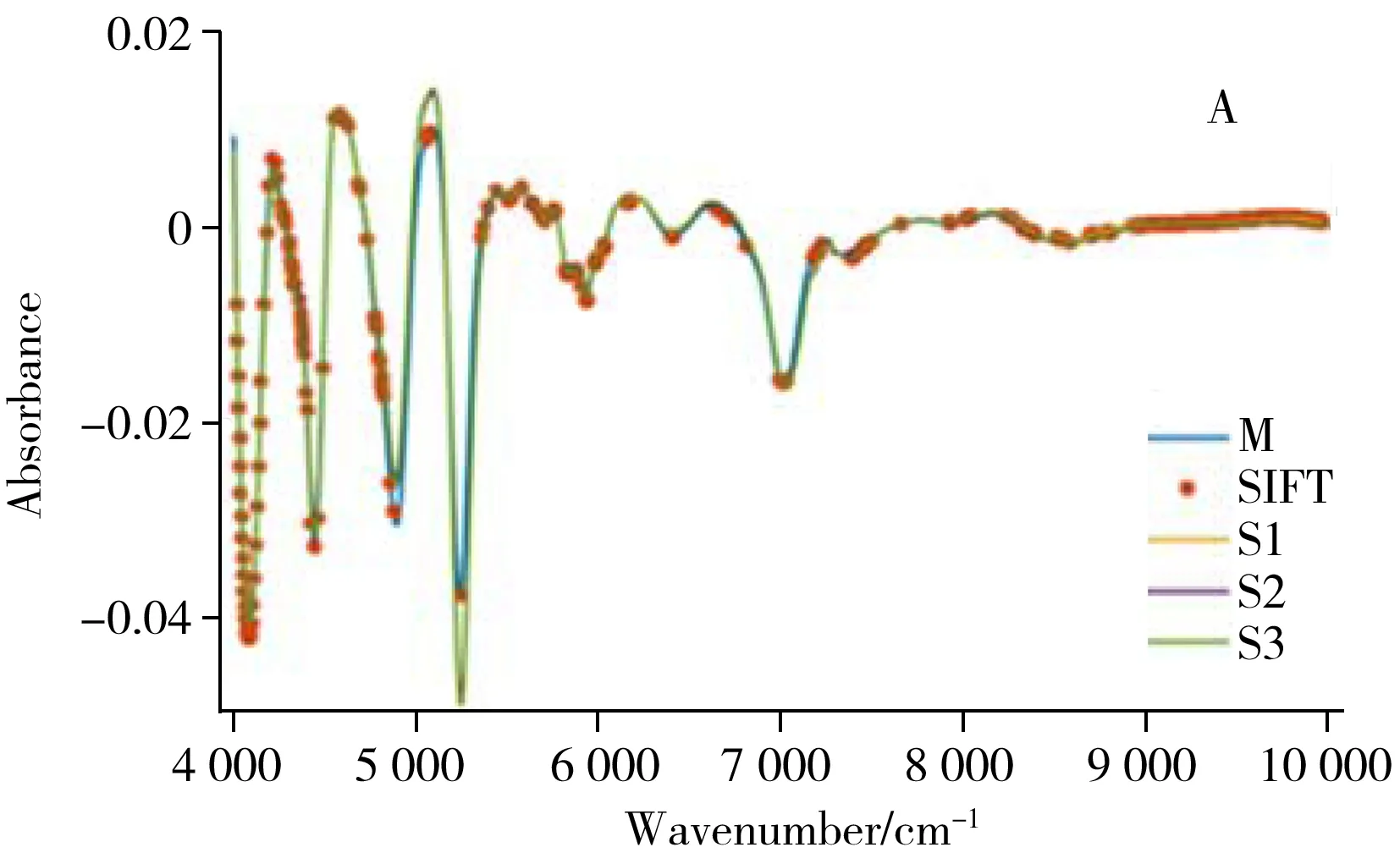
由图3可知,SIFT方法筛选出的大部分特征波长点在仪器间光谱差异很小的区域,那么以这304个波长的光谱响应为自变量,建立的烟叶总植物碱的SIFT-PLS光谱模型对主、从机样品预测结果应有良好的一致性。
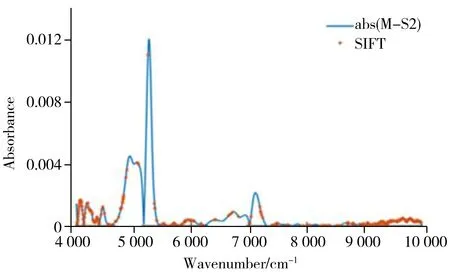
图3 主机M与从机S2的SNV+一阶导数光谱差谱的 绝对值及SIFT筛选波长Fig.3 The absolute difference spectrum between instrument M and S2 and the wavelengths selected by SIFT algorithm
3.3 不同烟叶总植物碱近红外光谱模型结果的比较
表4给出了SIFT-PLS模型、全波长PLS(Whole wavelength PLS,简称WW-PLS)模型以及WW-PLS模型与SIFT-PLS模型经PDS校正从机光谱后模型(PDS-WW-PLS、PDS-SIFT-PLS)的结果。从表4可以看出,WW-PLS在主机M以及从机S2上的预测误差满足企业内控要求(MRE<6%),其对另外2台从机样品的MRE均大于6%。经PDS校正从机光谱后,PDS-WW-PLS模型对S1、S3从机样品的MRE分别从9.13%、8.18%降为5.30%与6.12%,而对S2的MRE反而从3.85%增大到8.13%;SIFT-PLS模型预测S2从机样品总植物碱的MRE经PDS校正后从4.24%增大到4.88%。说明NIRS模型直接转移到从机的误差满足要求时,采用PDS校正反而会增大模型传递的误差;在模型传递误差较高时,PDS能起到一定改善作用,但也不能保证WW-PLS对3台从机的传递误差均满足企业内控要求。而SIFT-PLS模型对3台从机样品的MRE均满足小于6%的企业内控要求,当采用PDS校正从机光谱后,该模型对3台从机样品总植物碱的RMSEP均较SIFT-PLS模型直接转移有所降低,且PDS-SIFT-PLS模型对从机样品的MRE均低于PDS-WW-PLS模型。说明SIFT算法筛选波长所建模型较全波长模型更为稳健、精简,且PDS校正从机光谱后仍能保证SIFT-PLS模型对从机样品的MRE≤5%。
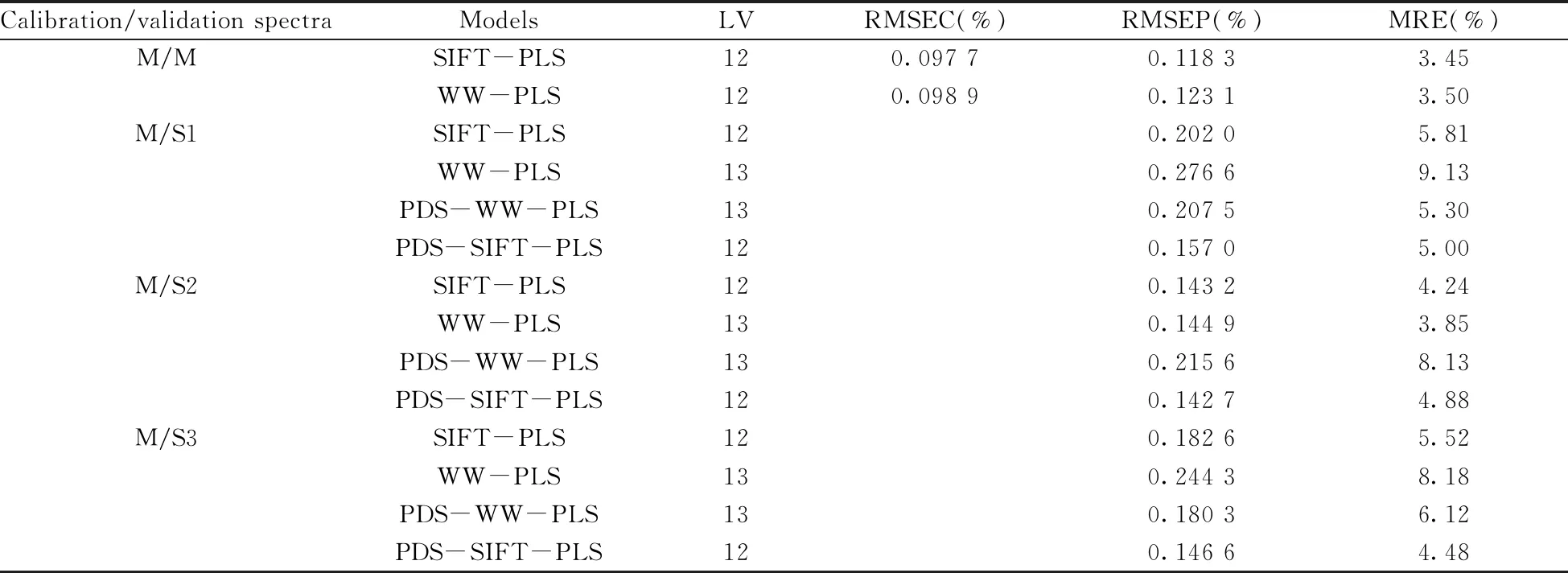
表4 不同烟叶总植物碱模型预测结果的比较Table 4 Results of total alkaloids contents predicted by different calibration models
4 结 论
利用SIFT算法筛选近红外光谱的关键点,波长筛选过程中无需从机样品信息,筛选出的波长点保留了光谱的主要特征,其光谱响应不随光谱尺度变化而改变,是样品光谱的稳定特征点,以这些波长下的光谱信息为自变量建立的烟叶总植物碱近红外光谱模型具有稳健、移植性好的特点。该模型直接转移到3台从机,无需任何模型传递方法进行从机光谱或模型校正,对从机样品总植物碱的MRE为4.24%~5.81%,经PDS算法校正从机光谱后,PDS-SIFT-PLS模型预测从机样品总植物碱的MRE为4.48~5.00%,均能满足企业内控要求;而PDS-WW-PLS模型预测两台从机样品总植物碱的MRE大于6%,表明全波长模型的稳健性和移植性均不及SIFT-PLS模型。
基于SIFT方法筛选近红外光谱的稳定特征波长建立烟叶总植物碱的近红外光谱模型,可实现模型的无标样传递,简便易行。该方法用于其他领域及样品的模型传递有待进一步验证。
