一种基于旋量理论的机器人关节结构误差对其精度影响的分析方法

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

工业机器人的精度一直是评价工业机器人工作要求的重要指标。机器人零部件加工阶段造成的尺寸和几何误差及装配过程中关节产生的间隙会对末端执行器位姿造成很大影响[1]。

分析机器人误差的方法有很多，如齐俊德等[2]对柔度误差的影响进行了解耦，并考虑了机器人基坐标系与测量坐标系的转换误差，提出基于相对位置的几何参数误差模型，该方法可有效提高机器人的绝对定位精度。张绍春等[3]提出一种利用Jacobi 矩阵将末端运动轨迹在Descartes坐标下的误差转换为关节角修正量的算法，有效降低了运动路径误差。刘华春等[4]利用基于关节刚度模型的位置补偿提高了重载机器人的末端轨迹定位精度。温秀兰等[5]在M-DH模型的基础上，提出基于拟随机序列产生初始位置的改进乌鸦搜索算法用于标定机器人几何参数，使得机器人精度大幅提升。随着机器人技术的发展，越来越多的现代方法[6-8]被应用到机器人的分析当中，旋量理论便是其中重要的一个。

为避免Denavit-Hartenberg模型（简称DH模型）的奇异性，K.Okamura 等[9]将Exponential of Product公式（简称POE 公式）应用到串联机器人的标定中，并建立了一般性的几何误差模型。谭月胜等[10]利用旋量理论建立了一模块化机械臂末端执行器运动误差数学模型。但是该模型只是将关节的误差影响设为6个结构参数的旋量，为隐式表达，并不能直接反映关节具体误差源的影响。黄勇刚等[11]将机器人关节轴线的位姿误差等效为假想广义运动副螺旋运动的结果，从而建立了误差模型，给出了其大小及方向的计算公式，但是在误差旋量建立时对理论关节轴线与实际关节轴线的位置关系只归结为相交、平行、交错3种情况，存在一定不足。Fu G.Q.等[12]提出了一种基于指数积公式的多轴机床的几何误差模型，该模型用3个旋量来表示每个轴的6个基础误差，满足精度要求，具有明确的几何意义。Qu S.W.等[13]利用有限位移旋量对串联机器人关节间隙对机器人精度的影响进行了分析。

本文基于旋量理论，提出了一种机器人关节结构误差对其精度影响的分析方法。通过对机械臂关节轴线在不同几何误差作用下位置空间关系的分析，给出了关节误差的旋量表达，结合POE模型，提出了包含具体误差源的机器人正向运动学显示表达式。并利用Adams 进行了仿真验证，仿真结果验证了本文提的方法的正确性。通过该方法可计算关节具体几何误差对机器人末端精度的影响，本文工作体现了旋量在机器人运动分析中的直观性、便捷性。提出的方法给机器人的制造、装配与优化以及机器人精度补偿研究提供了理论依据。

2 旋量及其表示

旋量是描述欧式几何空间的另一种几何元素。旋量的定义[14]：设s与s0为三维空间的2个矢量，其中s为单位矢量，s0=r×s+hs，则s与s0共同构成一个单位旋量，记作：

则刚体运动的指数坐标与POE 公式如下所示。

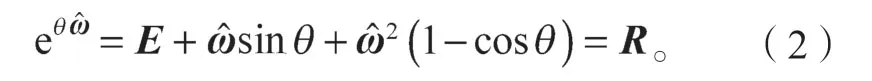
机器人各关节的运动由与之关联的关节轴线的运动旋量产生，如果用表示该关节轴线的单位运动旋量坐标，则沿此轴线的刚体运动可表示为

定义机器人初始位形为机器人对应于θ=0时的位形，并用表示机器人位于初始位形时惯性坐标系与工具坐标系间的刚体变换。对于每个关节都可以构造一个单位运动旋量这时除第i个关节之外的所有其他关节均固定于初始位形（θj=0，j表示除第i个并节角外其他的并节角度）。对于转动副：对于移动副：

这时，对于任意给定的n自由度机器人，指数积形式的正向运动学模型[15]为

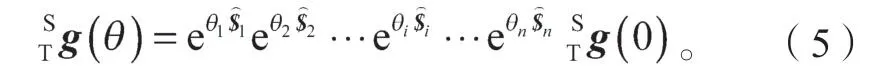
3 关节几何误差分析

机器人关节连接处出现偏差，即关节理论轴线与实际轴线不一致，根据其空间位置关系分为两轴重合（关节连接处发生轴向位移）、两轴平行、两轴线异面。显然理论轴线到实际轴线的运动为一般刚体运动，由Chasles定理[14]证明了刚体运动与螺旋运动是等价的。因此，可以用运动旋量来表示该运动，下面对上述情况进行具体分析。

当两轴线异面时可以视为理论轴线与实际轴线增加了一个螺旋副，理论轴线绕两轴线的公垂线旋转角度转∆θi，然后沿该垂线移动距离Δli。如图1所示。

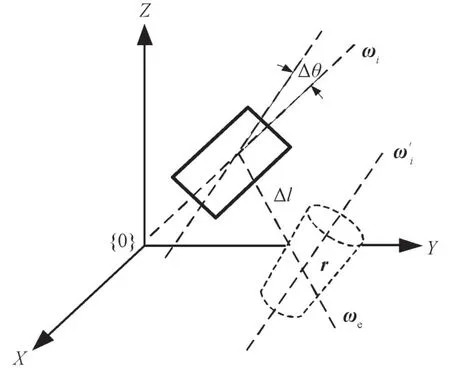
图1 两轴线异面Fig.1 Two axes on different surfaces

根据旋量的定义[14]，该螺旋副的单位运动旋量可以表示为

当节距为0时，单位旋量退化为线矢量，两轴线相交，仅发生旋转，如图2所示。

图2 两轴线相交且相对旋转Fig.2 Two axes intersecting with a relative rotation

此时，运动旋量可以表示为

当节距无穷大时，单位旋量退化为单位偶量，两轴线平行，仅发生径向平移，如图3所示。

图3 两轴线平行Fig.3 Two axes parallelling to each other

此时，运动旋量可以表示为

当两关节轴线共面且发生非径向移动时，可分为以下两种情况：发生轴向偏差、发生非轴向非径向偏移。可以视为理论轴线与实际轴线增加了一个移动副，如图4所示。

图4 两轴线共面且发生非径向偏差Fig.4 Two axes coplanar with non-radial deviation

此种情况下移动副的运动旋量可表示为

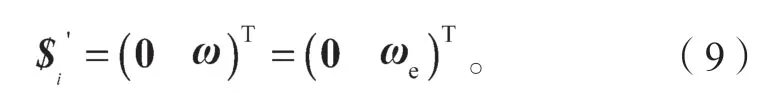
4 几何误差的旋量表达

文献[16]中指出：se(3)中的元素与SE(3)中的元素之间存在指数映射关系：任意给定齐次变换矩阵则必存在和标量θ，使得文献[13]给出和θ的计算公式。

当两轴线异面时，不妨设实际轴线是理论轴线绕x、y、z轴分别旋转角度∆、∆θ、∆ψ和移动距离∆x、∆y、∆z得到的。如图5所示。

图5 两轴线相对位置Fig.5 The relative position of two axes

因实际中不可能发生两轴线反向重合的情况，故不考虑trR=-1的情况。

两轴线关系为图1所示情况时，即：

有[13]

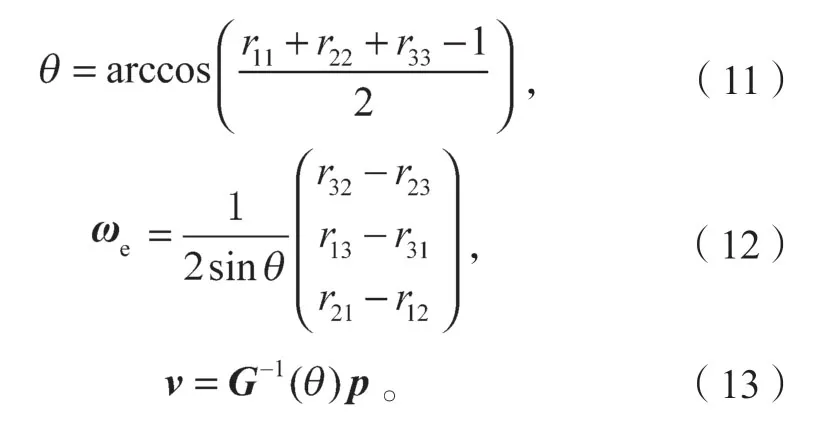
两轴线关系为图2所示情况时，即：

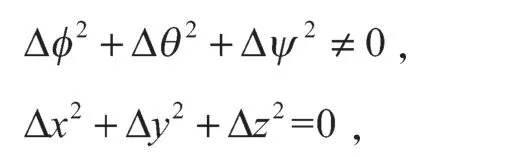
θ、ωe分别可由式（11）（12）求出，而v=(0,0,0)T。

两轴线关系分别为图3、图4a、4b所示情况时，即：

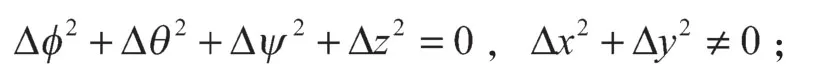
此时有[13]：

式中：gi为i号关节坐标系相对于空间坐标系的姿态矩阵。

5 仿真验证

5.1 机械臂模型

在Matlab中建立了如图6所示的3R 机械臂模型，其中连杆长度设置如下：L1=520 mm，L2=350 mm，L3=250 mm。机器人关节轴线单位矢量及点的设置如表1～2所示。

图6 3DOF 机械臂模型图Fig.6 Model drawing of 3DOF robot manipulator

表1 机器人关节轴线单位矢量Table1 Unit vector of robot joint axis

表2 机器人关节轴线上的点Table2 Points on the robot joint axis

机器人位于初始位形时，惯性坐标系与工具坐标系间的刚体变换矩阵为

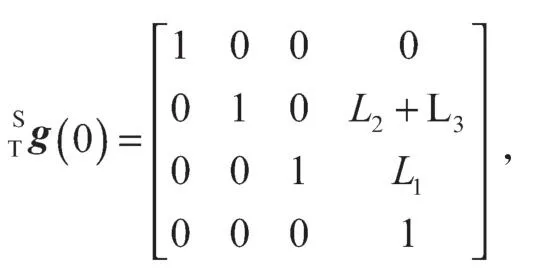
各关节运动旋量为

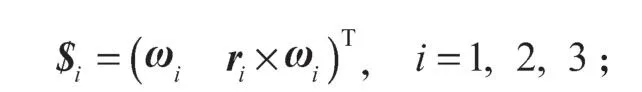
机器臂正向运动学的指数积公式为

根据式（19）考虑关节误差后得到的机器臂实际正向运动学公式为

让机械臂沿如图7所示的一段起点坐标为(0.00,600.00,520.00)，终点坐标为(214.05,370.75,128.49)的空间轨迹运动，记录各关节角度值的变化。

图7 末端运动轨迹Fig.7 Trajectory of the end effector

将各关节误差设置成如表3所示的误差值，将上述记录的各关节角度值代入式（20），得到包含误差的轨迹坐标值，然后将该坐标值与不包含误差时的轨迹坐标相减得到如图8所示的误差曲线图。

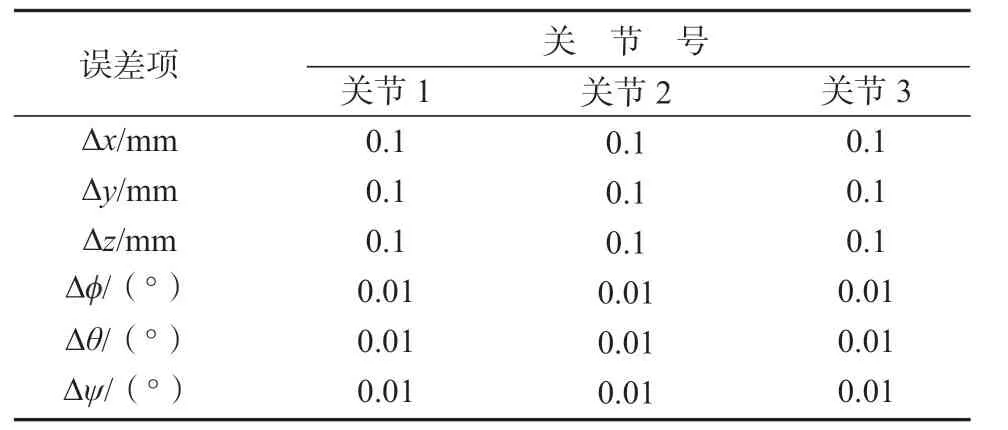
表3 关节误差值Table3 Joint error value

图8 末端位置误差曲线Fig.8 Position error curve of the end effector

5.2 Adams 仿真验证

根据图6所示的结构，利用SolidWorks 软件建立了机械臂的三维模型。在模型装配阶段，通过调整部件的旋转与位移，将如表3所示的误差值添加进各关节，然后将模型导入Adams 里，得到如图9所示的三自由度机械臂模型。

图9 3DOF 机械臂Fig.9 3DOF robotic manipulator

在两相邻连杆间添加如图10所示的旋转关节，各关节的Marker点坐标如表4所示。给各旋转关节添加如图11所示的Motion，Motion 由5.1中各关节产生的角度值生成的样条曲线驱动。

图10 各关节设置Fig.10 Settings of joints

表4 Marker点坐标值Table4 Coordinate values of marker points

图11 Motion 设置Fig.11 Motion settings

通过仿真实验，获得了机械臂运动时末端各位置的坐标，并将各坐标数据导出后与5.1中不包含误差的坐标数据相减，得到如图12所示的末端位置误差曲线。

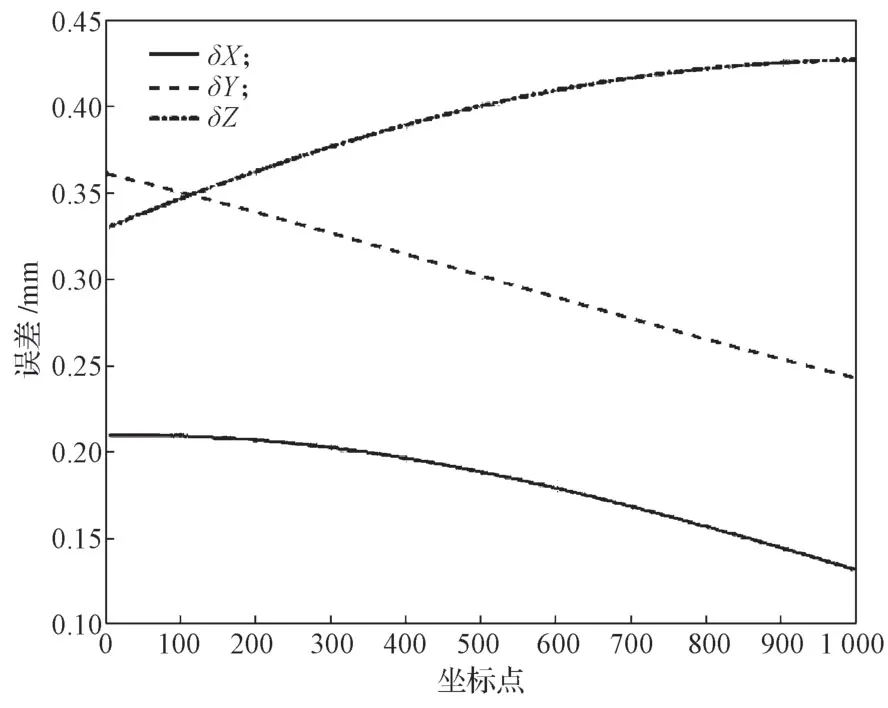
图12 末端位置误差曲线Fig.12 Position error curve of the end effector

同时将仿真数据与公式计算的包含误差的坐标数据相减，得到如图13所示的坐标差值图。

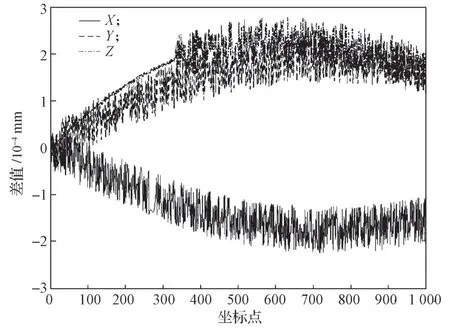
图13 仿真结果与公式计算结果的坐标差值Fig.13 Coordinate difference between simulation results and formula calculation results

从图8与图12所示的误差曲线可以看出，公式计算与仿真实验得到的误差值基本一致，注意到图13中仿真得到的数据与式（20）计算的坐标值并不完全一致，但两者的差值在（±3×104）mm 以内，考虑到仿真软件中数值运算存在一定的精度限制，故将图13所示的误差认定为合理的误差。由此，本文提出方法的正确性得到了验证。

6 结语

课题组应用旋量理论，通过分析机器臂关节两轴线在不同几何误差作用下的位置空间关系，将关节误差表示成旋量的形式，结合POE 公式，给出了包含关节误差的机器臂正向运动学公式。通过对一3R 关节机械臂的仿真实验，验证了课题组提出的精度分析方法的正确性。该方法体现了旋量在机器人运动分析中的直观性、便捷性，为机器人的制造、装配与优化提供了参考依据，可以提高工业机器人的定位精度。该方法不仅可用于静态和准静态误差分析，如果考虑误差的大小随机构运动过程变化，还可用于动态误差的分析。