基于d维GHZ态的多方量子密钥协商*
2020-11-06唐杰石磊魏家华于惠存薛阳武天雄
唐杰 石磊 魏家华 于惠存 薛阳 武天雄
(空军工程大学信息与导航学院, 西安 710077)
1 引 言
随着量子信息技术的发展, 量子密码也因其无条件安全性引起越来越多的关注. 不同于经典密码, 量子密码的安全性并非基于解决数学难题的复杂性, 而是基于量子物理学的基本原理, 从理论上讲具有无条件安全性. 量子密码技术包含很多分支, 如量子密钥分发, 量子安全直接通信, 量子秘密共享.
在开放式、动态化的网络中, 为了满足网络中的认证, 临时会话等需求, 实现保密通信, 在一个公开、不安全的信道中建立会话密钥, 两个端节点之间需要建立一个共享的密钥来实现基本的安全需求. 基于此, 量子密钥协商 (quantum key agreement, QKA)则引起了研究者们广泛的关注.不同于量子密钥分配, 量子密钥协商是一种双方或多方共同合作建立共享密钥的技术. 在协议中, 每个参与者均不能事先单独决定共享密钥, 且他们对于最终生成的密钥贡献相同. 在量子保密通信中,需要建立临时通话, 满足网络中的认证等, 而量子密钥协商恰恰适应这个要求, 使我们可以安全地在分散型、无管理和动态网络结构中建立共享密钥.因此, 量子密钥协商具有重要的研究意义.
自2004年Zhou等[1]利用量子隐形传态和最大纠缠态提出第一个QKA协议起, 人们陆续提出了很多QKA协议[2−8]. 然而, 这些QKA协议仅仅只涉及两方, 并不适用于多个参与者. 自Shi和Zhong[9]基于EPR对和纠缠交换将两方QKA协议拓展到多方量子密钥协商 (multi-party quantum key agreement, MQKA)协议时, 研究者们也将关注点放在了MQKA协议中. 随后 Liu等[10]指出Shi和Zhong提出的MQKA协议是不安全的, 证明了不诚实的参与者能够独自决定共享密钥, 同时他们提出了一种仅使用单光子进行编码的MQKA协议来抵抗参与者内部攻击. 然而, Liu等的协议效率不是很高. Sun等[11]添加了两个幺正操作改进了Liu的协议, 将量子比特效率提高到了1/[N(k+1)]. 同年, Yin 等[12]基于两粒子纠缠态提出了三方QKA协议. 2014年, Xu等[13]基于GHZ(Greenberger-Horne-Zeilinger)提出一个 MQKA协议, 协议中的每个参与者仅仅只需执行单粒子测量. 后来, Sun等[14,15]利用六粒子簇态提出两个MQKA 协议. 2018 年, Cai等[16]基于五粒子 brown态和单粒子测量提出一个MQKA协议. 相比于其他协议, 此协议的效率更高, 并且也有着更好的操作灵活性. 2019 年, Lin 等[17]发现 Cai等的协议不满足协议的公平性, 并提出了一个改进的协议. 同年, Liu等[18]利用四粒子簇态作为量子源, 并对粒子执行X基操作, 提出了一个新的MQKA协议.效率分析也说明此协议拥有着较高的效率. 2020年,Zhou等[19]以量子方Charlie, 经典方Alice和Bob为参与方提出三方半量子密钥协商协议(semi-QKA). 此协议能够减少量子设备的使用, 降低损耗. 随着对量子密钥协商协议的研究逐渐深入, 为了追求更好的安全性、公平性和高效率, 人们提出了许多MQKA协议[20−29].
“d维”这个概念在量子密码的其他协议中出现过多次, 但在量子密钥协商中并未有人做过太多研究. 本文基于d维k粒子GHZ态提出了一个多方量子密钥协商协议. GHZ态最早由Greenberger-Horne-Zeilinger三人联合提出. 1999年,Bouwmeester等[30]通过实验对其进行了观察与分析, 发现其显著的作用. 在后来的研究中, GHZ 态被广泛应用于多方量子密钥分发[31,32]、多方量子秘密共享[33]和多方量子安全直接通信[34]等方向. 本文所提的d维多粒子GHZ态是二维GHZ态的衍生, 能够携带更多的信息, 具有更高的信道容量.除此之外, 在我们提出的多方协议中, 多个参与者是完全对等且公平的, 并利用时移操作将密钥编码到量子序列中, 最后通过d维Z基测量得到密钥.安全性分析表明本方案能够有效地抵抗内部参与者和外部窃听者的攻击.
2 基于d维GHZ态的MQKA协议
2.1 理论基础
对于d维量子系统来说,k粒子GHZ态可表示为

两组正交基分别表示为

其中QFT是指作用在d维Hilbert空间的离散量子傅里叶变换, 它的作用是把一个单态转换到一个叠加态. QFT的定义为

接下来, 引入时移操作:
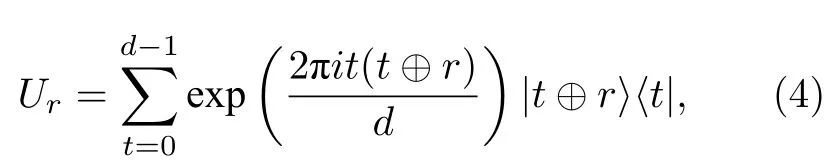
其中t⊕r表示t+r模d. 经过验算, 不难发现,
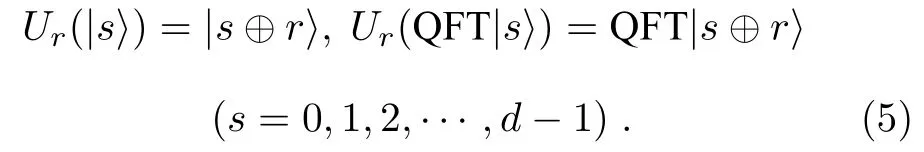
2.2 提出的MQKA协议
本节介绍提出的基于d维k粒子GHZ态的MQKA 协议. 假设P0,P1,P2,···,Pk−1是 协 议的k个参与者, 他们想通过量子信道建立共享密钥K,每个参与者Pi随机产生各自的密钥信息为d=2l+1;n=0,1,···,k−1 ;j=0,1,···,d−1 .协议的具体步骤如下.
第1步每个参与者Pi准备好m个形式如(1)式的d维k粒子GHZ态, 并将每一个GHZ态分成k个粒子序列:S0,S1,···,Sk−1, 其中第i个序列Si(i=0,1,···,k−1) 由GHZ态的第i个粒子组成. 接下来,Pi从(2)式的X基和Z基随机挑选诱骗态分别插入到每个序列Si(i=0,1,···,k−1)中得到新的序列(i=0,1,···,k−1) , 并将序列(j=0,1,···,k−1)发送给其他参与者Pj.
第 2 步在确认Pj接收到序列后,Pi将诱骗态的位置、采用的测量基及测量结果告知Pj, 双方进行第一次安全检查.Pj用相应的测量基测量诱骗态粒子, 并根据测量结果对信道进行安全性检查, 若测量结果的错误率超过约定的阈值, 则认为协议中存在窃听者, 终止本次协议并重新开始; 若没有超过约定的阈值, 则Pj从序列挑选出诱骗粒子并舍弃, 将其恢复成Sj.
第3步每个参与者Pj随机挑选一组序列并对序列Sj的第t个粒子进行如(4)式所示的时移操作得到新的粒子序列随机挑选诱骗态插入到序列中得到新的序列, 并将其返还给Pi.
第4步在确认Pi收到序列后, 双方进行第二次安全性检查, 检查过程与第2步类似. 若测量结果的错误率超过约定的阈值, 则认为协议中存在窃听者, 终止本次协议并重新开始; 若没有超过约定的阈值,Pi舍弃其中的诱骗态恢复序列. 接下来,Pi用Z基测量序列中的每个粒子并得到Pj随机挑选的序列rj的值.
第5步Pj将其密钥加密为其中加密规则为随后,Pj通过认证信道将其发送给Pi.
第6步Pi通过序列rj的值和Pj发送过来的, 计算得到每个参与者Pj的密钥Kj, 并计算出最终共享密钥K=K0⊕K1⊕···⊕Kk−1.
2.3 MQKA协议的一个例子
在本节中, 将给出上述协议的一个特例. 为了方便讲解, 在例子中并不考虑两次安全检查. 首先,令k=3 ,l=3 ,d=2l+1=7 . 其次, 假设 3 个参与者P0,P1,P2的密钥分别为K0=(1,3,2,2,3,1,2) ,K1=(3,1,2,1,1,3,2),K2=(2,3,2,2,1,3,1) , 以P0为例.
第1步P0准备好m个7维三粒子GHZ态并将其分成 3 个粒子序列:S0,S1,S2. 随后,P0将S0留在手中, 将S1发送给P1, 将S2发送给P2.
第 2步P1,P2分别随机挑选一组序列r1=(1,3,5,3,4,2,3),r2=(3,6,2,3,1,4,5) , 并 分别对其持有的粒子序列S1,S2的第t个粒子执行时移操作随后, 将操作后的粒子序列发给P0.
第3 步此时,P0拥有的3 粒子GHZ 态变为
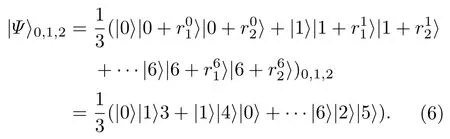
P0用Z基测量中的每个粒子并得到序列r1和r2的值.
第4步P1,P2分别将其密钥K1,K2加密为通过认证信道将其发送给P0.
第 5 步P0通过序列r1,r2的值和Pj发送过来的计算得到P1,P2的密钥K1,K2, 并计算出最终共享密钥K=K0⊕K1⊕K2= (6, 0,6, 5, 5, 0, 5).
3 安全性分析
QKA协议主要涉及两类攻击: 参与者攻击和外部攻击. 其中外部攻击又可以分为木马攻击、截取重发攻击. 为了证明这些协议的安全性, 将根据这两种攻击来讨论.
3.1 参与者攻击
假设参与者P0为不诚实者, 想要获取其他参与者的密钥. 首先,P0需要得到序列rj. 然而,rj为Pj随机选择的序列, 故P0只能够通过在协议的第3步进行截取重发攻击获得粒子序列. 此时, 参与者攻击可看成外部攻击, 并且其攻击将会在协议的第二次安全检查中被发现, 造成协议的失败. 而在第5步中, 其传输是通过认证的量子信道, 故P0不能获得任何关于rj的信息. 此协议可以抵抗内部参与者攻击.
3.2 外部攻击
假设Eve是外部攻击者, 她需要窃听rj和的信息来获得共享密钥. 可能的主要攻击方法有特洛伊木马攻击、拦截重发攻击和纠缠测量攻击.
特洛伊木马攻击. 由于这个改进的协议是一个单向的QKA协议, 所有的粒子序列只在信道中传输一次, 特洛伊木马攻击者没有机会从粒子序列中提取出间谍光子. 也就是说, 改进的协议可以不需要使用任何特定的检测设备, 从而能够抵抗两种类型的攻击特洛伊木马攻击[35,36].
纠缠测量攻击. 在两个协议中, 假设Eve想要利用自己事先准备的辅助光子对QKA协议进行纠缠测量攻击, 则她需要对截获的量子态执行幺正操作UE使之与辅助光子产生纠缠. 以免疫集体退相位噪声的QKA协议为例, 结果如下.
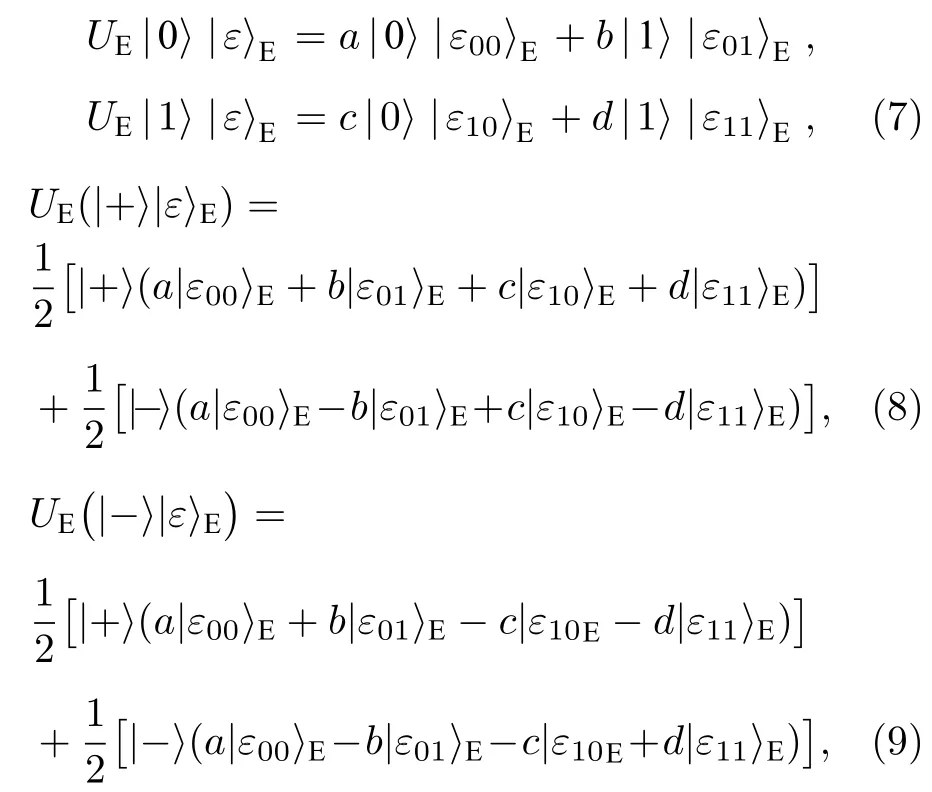
其中|a|2+|b|2=1 ,|c|2+d2=1 . Eve 为了避免引入错误, 必须满足
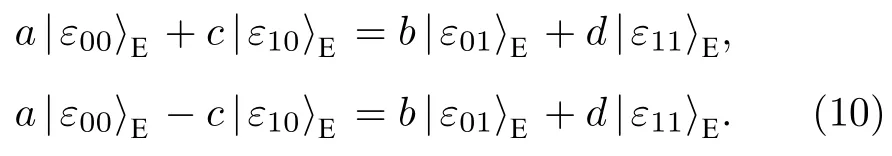
(10)式必须满足三个条件:a=d=1 ,b=c=0 ,则 (7)式变为

从本节的分析可以得出, 我们的协议不但能够抵抗内部参与者的攻击, 还能够抵抗外部窃听者的攻击. 而当内部攻击与外部攻击同时发生时, 协议能够通过进程及时知晓, 并及时止损, 不造成任何信息的泄露.
4 效率分析
正如Cabello在文献[37]中所述, QKA协议的量子比特效率可以定义为其中,c是最终密钥的长度,q是所用量子比特的数目,b是用于生成最终密钥所用经典比特的数目. 在本方案中, 准备了m个d维k粒子GHZ态, 在每次量子序列的传输过程中插入d个诱骗粒子. 因此本方案的量子比特效率同时, 我们的协议与其他多方QKA协议的比较如表1所列. 相比于其他协议, 我们的协议也有着较高的量子比特效率.

表 1 本文协议和其他协议比较Table 1. Comparison between our protocols and the other protocols.
5 结 论
本文基于d维k粒子GHZ态提出了一个多方量子密钥协商方案. 通过时移操作将密钥编码到序列中, 并以d维Z基测量得到序列中的密钥, 最后对所有参与者的密钥进行异或操作建立共享密钥.安全性分析表明我们的方案能够有效地抵抗内部参与者和外部窃听者的攻击. 然而, 我们的协议提出的前提是基于理想环境下的量子信道. 在实际应用中, 粒子在有噪量子信道传输过程中, 通常会受到噪声的影响. 因此, 在将来如何使本协议适应更加复杂的环境是我们研究的重点.
