层裂损伤孔洞增长模型参数的确定方法及其应用*

张凤国 刘军 何安民 王裴 王昆 周洪强 赵福祺

(北京应用物理与计算数学研究所, 北京 100094)

1 引 言

冲击载荷作用下, 反射冲击波在靶板内部叠加形成拉伸作用区域, 当拉伸应力足够高时, 延性材料内部层裂面处经历孔洞的成核、增长、汇合直至材料断裂破坏的损伤演化过程, 即层裂破坏. 包括爆轰加载、撞击以及激光加载等均可能造成结构材料的层裂破坏, 因而该问题的研究具有重要的实用价值. 同时, 层裂属于一维拉伸破坏问题, 应力状态简单、实验易行, 研究层裂损伤演化过程也有助于分析材料的理论强度、揭示材料的损伤断裂机理[1−3].

在层裂损伤问题的研究历程中, 为了数值模拟分析材料的损伤演化过程及其对结构的影响, 采用的损伤模型不断发展完善, 从最初的瞬时断裂模型、损伤累积模型到目前采用的耦合材料微细观结构信息的损伤累积模型[4−10], 使得对损伤演化过程的描述逐渐精细化, 同时, 结合实验和理论研究深入探讨损伤演化特性[11−20], 逐步加深了对材料损伤微细观机理的认识. 在层裂损伤模型的发展过程中, 人们过多地关注如何完善损伤模型, 更好地使计算结果与材料内部损伤状态相符合, 而忽略损伤模型参数如何标定这一重要问题. 对于一些损伤模型, 模型参数的改变不仅对计算结果的影响很大,而且模型参数本身也可能是相关的, 同时, 部分参数的选取具有一定的人为性, 这就为损伤模型的具体应用造成了困扰, 也降低了计算结果的可信度.以目前应用较为广泛的孔洞增长VG模型(void growth model)[5]为例: 该模型考虑了基体材料的率效应, 并基于空心球壳得到了孔隙度α(空心球壳总体积与基体体积之比)随时间变化的增长率与外加拉伸载荷p之间的关系为(本文中变量对时间的导数“ d /dt”均表示为“.”)

模型包含的三个基本参数: 初始孔隙度α0定义为距离层裂面较远处的孔隙度, 这个定义本身具有人为性;η为剪切黏性系数, 但实际应用时作为计算参数, 并根据实验数据进行调整; 基于理论推导,系 数αs与 基 体 材 料 的 屈 服 强 度Y0相 关 , 即αs=2Y0/3, 而实际应用时, Johnson[5]定义其为与孔洞周围基体材料的硬化强度相关, 同样也为计算参数. 此外, Johnson[5]的文章中只是给出了OFHC高纯铜材料的损伤模型参数, 对于其他材料, 参数如何确定就值得商酌, 这极大地降低了计算结果的可信度. 同时, 三个参数的改变也直接影响了损伤演化过程的宏观外在表现——自由面速度变化.图1给出了采用VG模型计算模拟的飞片撞击靶板的自由面速度, 计算结果显示, VG模型参数的选取不同将导致靶板材料发生损伤破坏(速度曲线有回跳)或没有损伤产生(速度曲线没有回跳)两种极端情况. 因此, 需要进一步解析损伤模型参数所包含的物理涵义, 给出参数的确定方法.

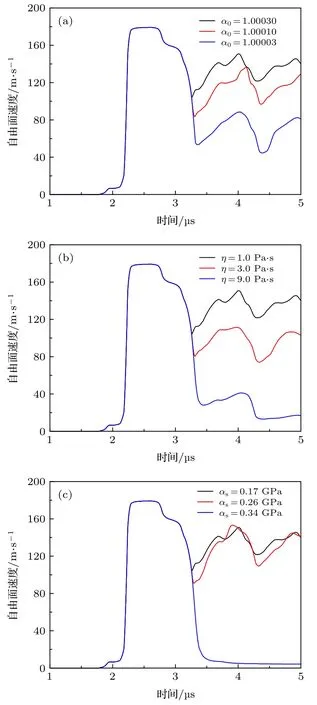
图 1 损伤模型参数对自由面速度的影响 (a) 初始孔隙度的影响; (b) 剪切黏性系数的影响; (c) 材料硬化参数的影响Fig. 1. Influences of spall model parameters on free surface velocities: (a) Effects of initial porosity; (b) effects of shear viscosity; (c) effects of work hardening.

本文结合自由面速度曲线的斜率和回跳点等变化特性与层裂面处损伤演化过程之间的对应关系、损伤与应力改变之间的关联等, 进一步解析损伤模型参数所包含的物理涵义, 探讨基于物理的损伤模型参数的确定方法, 并通过与文献中不同延性金 属材料的层裂实验数据比较, 验证了该方法的合理性.

2 层裂损伤模型参数的确定方法

层裂损伤机理认识的不断提高得益于近年来实验诊断技术的进步, 其中基于VISAR, DISAR等光学表面诊断技术获得的自由面速度曲线是认识层裂损伤演化规律最重要的一个窗口.根据波的相互作用理论, 层裂面处的损伤演化与自由面速度曲线的变化之间存在间接的对应关系, 因此, 深入解读自由面速度曲线的变化特性有助于揭示材料内部的损伤变化机理和损伤模型的物理建模.

随着层裂损伤研究的深入, 人们对自由面速度曲线的认识不断提高. 图2显示了2 mm飞片以185 m/s的速度撞击 9 mm OFHC 高纯铜靶板的自由面速度实验测量结果[21]. 冲击波达到自由面后, 速度达到峰值, 之后冲击波在自由面反射形成卸载稀疏波, 速度曲线下降达到第一个低点, 即回跳点, 峰值与回跳点之间的速度差 ∆u与靶板内部层裂面处卸载稀疏波相互叠加引起的拉伸应力相关, 即层裂强度; 回跳点左侧曲线下降斜率与拉伸应力的增长率相对应, 而右侧速度曲线上升的斜率与材料内部损伤增长率相关[2]. 对于回跳点所包含的物理涵义, 近期的实验分析和研究表明:自由面速度曲线的回跳信号不是材料完全分离的一个标志, 其与孔洞的成核以及早期增长相关, Tonks等[6]定性给出其对应的孔隙度近似为1.0005. 结合文献关于材料弹塑性效应对层裂损伤影响的分析[22], 可以进一步明确回跳点对应层裂面处因孔洞早期增长引起材料完全塑性变形的时刻, 此时刻的临界孔隙度为

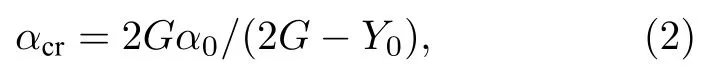
其中G为剪切模量, 对应的临界应力-层裂强度的计算采用1980年Romanchenko和Stepanov[23]给出的公式:

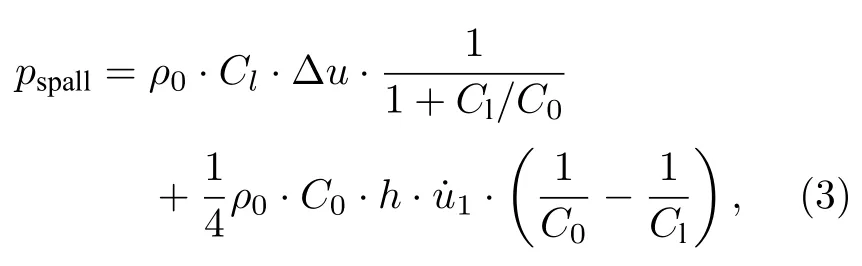
其中,ρ0为初始基体材料密度,Cl为基体材料的纵波声速,C0为体积声速,h=0.5Cl·∆t, 为层裂片厚度.

图 2 自由面速度曲线典型特征Fig. 2. Characters of free surface velocity profile.

首先, 计算过程中采用的含损伤格林内森状态方程的微分形式可以表示为

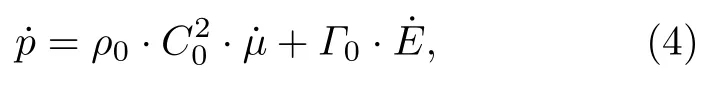
其中Γ0为格林内森系数,E为单位初始体积内能,体积应变µ=ρ/ρ0−1 ,ρ为当前基体材料密度. 对于一维层裂损伤问题, 在基体材料不可压的假设条件下,而内能的改变量为

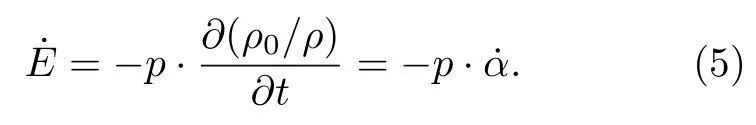
将 (5)式代入 (4)式并积分 (α0到αcr), 同时考虑在孔洞早期增长过程中则有

考虑到p0=αsln[α0/(α0−1)], 代入 (6)式有:

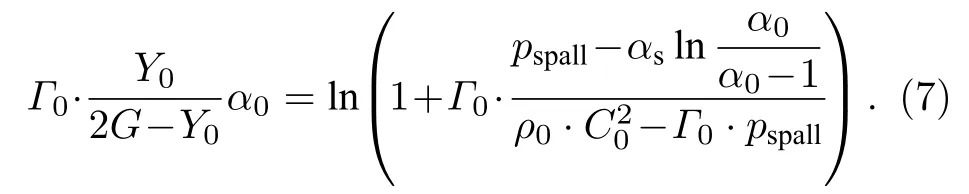
其次, 在确定模型参数时, 只需讨论孔洞早期增长过程, 即则 (1)式可以近似改写为

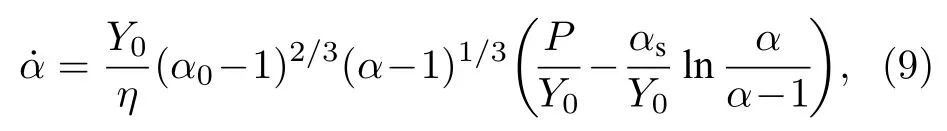
其中P/Y0为体现加载强度的无量纲量, 而包含材料特性的系数 (α0−1)2/3Y0/η本身的量纲只与时间相关, 因此, 不妨假设将其值定义为与材料无关的常数, 结合 Johnson 给出的数据, 即有

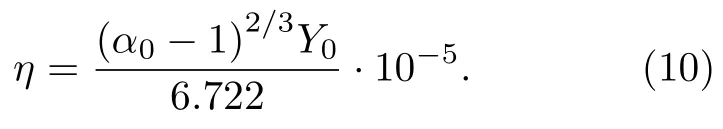
最后, 当自由面速度曲线回跳时, Antoun等[2]给出了其对应层裂面处的孔隙度增长率为为拉伸应力开始增长时的应力率,同时, 根据波的相互作用有则有

结合(1)式可以得到:

至此, 基于理论推导, 并结合自由面速度曲线的实验结果, 本文给出了VG层裂损伤模型参数的确定方法: (8)式、(10)式、(12)式均对应速度回跳时刻各物理量之间的关系, 联立(8)式、(10)式、(12)式可以数值求解VG模型的三个参数α0,η和αs; 也可以将(8)式和(10)式代入(12)式, 利用数学软件Mathematica中FindRoot命令求解参数α0, 然后代入(10)式和(12)式得到其他参数. 同时指出, 参数α0并非实际的初始孔隙度, 而是参考初始孔隙度; 自由面速度曲线回跳点对应层裂面处材料因孔洞增长达到塑性变形; 此外, VG模型虽然简单、实用, 但因为没有考虑惯性和材料微结构的影响, 模型本身并不完善, 这使得参数η和αs虽然赋予了一定的物理涵义, 而实际上属于调整损伤增长的模型参数.

3 参数确定方法的实验验证

为了验证本文给出的参数确定方法的适用性, 这里采用数值方法模拟两种典型延性金属材料OFHC铜和钽的层裂实验给出的自由面速度剖面. 延性金属材料的层裂损伤演化属于从微观的孔洞成核、增长到宏观破坏的多尺度问题, 相对而言, 基于微观物理机理的ZA本构方程更适合层裂损伤的计算[24,25].因此, OFHC铜本构方程选用针对FCC材料的ZA本构方程:

表 1 OFHC 铜和钽的基本力学参数Table 1. Material parameters of OFHC copper and tantalum.

表 2 OFHC 铜和钽的 ZA 本构模型参数Table 2. Material parameters of OFHC copper and tantalum for Zerilli-Armstrong constitutive relations.

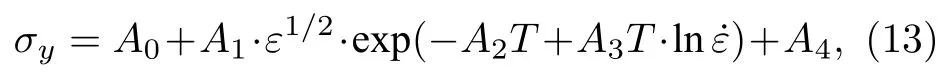
金属钽的本构方程选用针对BCC材料的ZA本构方程:

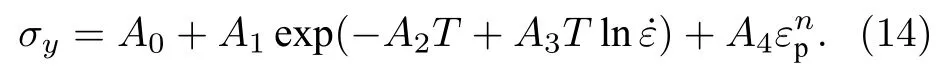
两种金属的基本材料参数[25,26]见表1和表2.

首先, 采用上述方法确定OFHC高纯铜材料的VG层裂损伤模型参数. 基于图2给出的层裂实验的自由面速度曲线[21]有: 速度差 ∆u= 65.2 m/s、曲线斜率根据波的相互作用, 飞片加载层裂实验的层裂片厚度近似为飞片厚度, 即h= 2 mm, 则由 (3)式计算得到层裂强度pspall= 1.682 GPa. 根据 (8)式、(10)式和 (12)式计算得到:α0= 1.00048;η= 1.368 Pa·s;αs=0.193 GPa. 图3显示了采用VG模型原参数和本文给出参数计算得到的自由面速度曲线与实验测量结果均符合较好. 此外, 若取α0= 1.0003, 则根据 (8)式和 (10)式得到η= 1.0 Pa·s以 及αs=0.182 GPa, 这与 Johnson 给出的α0= 1.0003,η=1.0 Pa·s以及αs= 0.17 GPa 近似相同. 总体而言,对比结果表明: 1)新的参数标定方法不仅可以还原VG层裂损伤模型的参数, 而且基于实验和物理给出的参数也能够很好地模拟自由面速度变化情况(对应材料内部的层裂损伤演化过程), 证明了本文给出的参数标定方法的有效性; 2)从另一个角度而言, 同一个物理模型有两套有效参数, 这也说明层裂损伤模型本身还不完善.

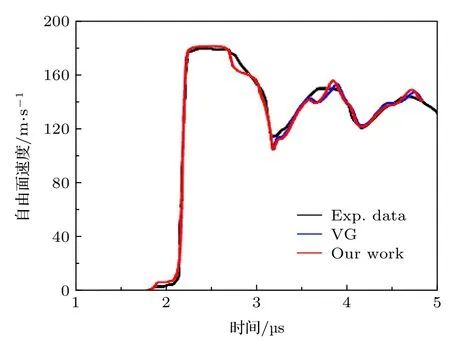
图 3 OFHC 铜层裂的自由面速度曲线Fig. 3. Simulated free surface velocity profile for OFHC copper.

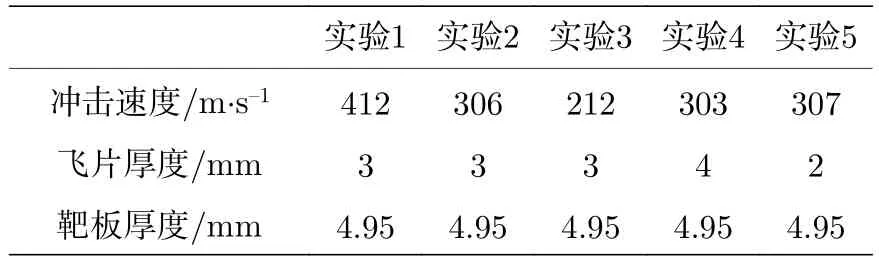
表 3 实验列表Table 3. Parameters of shock experiments.

进一步验证本文给出的参数确定方法合理性的关键是采用VG模型对其他延性金属材料层裂实验结果的有效计算模拟, 这里包含两个层次的验证: (10)式假设条件的成立以及参数确定方法的合理性. 金属钽是研究金属材料层裂损伤机理的常用典型延性金属之一, 表3列出了文献给出的不同加载速率和不同加载飞片厚度的5发实验: 对比实验1—实验3, 飞片和靶板厚度相同, 飞片的撞击速度不同, 实验反映了加载强度对自由面速度(损伤)的影响; 对比实验5、实验2和实验4, 靶板厚度相同, 飞片的撞击速度近似, 但飞片的厚度不同,实验反映了飞片厚度(即加载应变率)对自由面速度(损伤)的影响[17]. 本文根据实验2的自由面速度剖面特征确定VG模型参数: 层裂片的厚度近似为飞片厚度, 即 3 mm, 自由面速度曲线速度差 ∆u=134.2 m/s、曲线斜率由(3)式计算得到层裂强度pspall= 5.18 GPa, 再根据 (8)式、(10)式和 (12)式计算得到:α0= 1.00676;η= 37.23 Pa·s;αs= 0.8506 GPa. 这里可以看出:高强度延性金属钽的初始孔隙度α0远远大于铜的初始孔隙度, 这与原文提到的初始孔隙度的概念相悖, 从而说明了初始孔隙度应定义为VG损伤模型应用时的参考初始孔隙度.

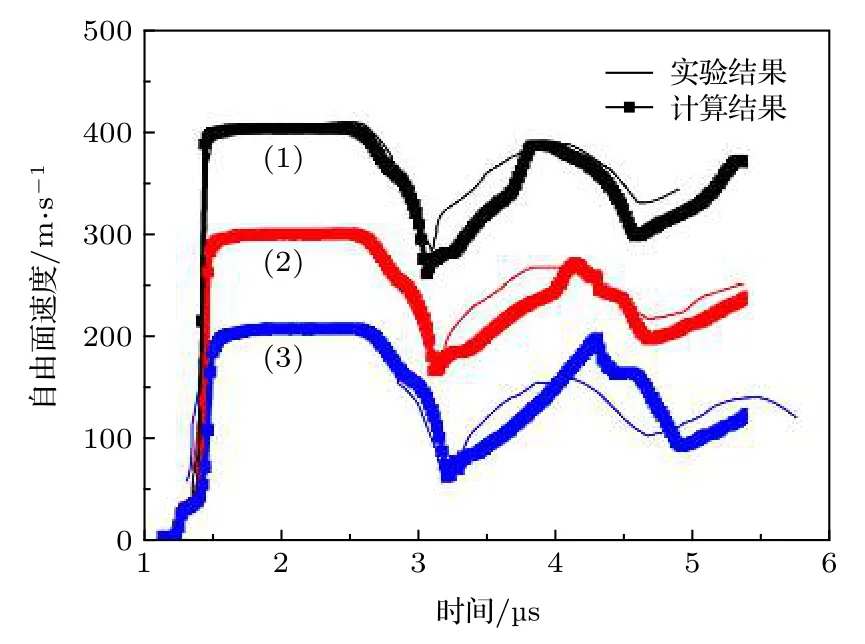
图 4 不同飞片撞击速度的自由面速度曲线Fig. 4. Simulated free surface velocity profiles with varied impact velocities.

图 5 不同飞片厚度的自由面速度曲线Fig. 5. Simulated free surface velocity profiles with varied flyer thickness.

采用VG模型和本文给出的参数, 图4给出的是不同撞击速度加载条件下层裂实验1—实验3的自由面速度观测结果和计算模拟结果, 图5给出的是不同飞片厚度在相近撞击速度加载条件下层裂实验5、实验2和实验4的自由面速度观测结果和计算模拟结果. 采用相同参数对不同实验模拟对比发现: 首先, 对于速度曲线回跳后上升的斜率,模拟结果与实验结果相差较大, 这可能是VG损伤模型本身没有考虑惯性影响的原因[22]; 其次, 对于层裂损伤分析所关注的自由面速度回跳点、回跳后曲线上升的幅值以及回跳后曲线的振荡周期 ∆t,模拟结果与实验结果均符合较好, 从而验证了参数确定方法的适用性; 最后, 因可以较好模拟不同加载强度和加载应变率实验结果, 也说明本文给出的参数确定方法可以较好地适用于飞片撞击加载的层裂损伤问题研究.

采用本文给出的参数确定方法, 通过对不同材料、不同加载环境下层裂损伤实验结果的有效模拟, 一方面验证了(10)式所给出的假设条件具有一定的合理性, 另一方面也验证了模型参数确定方法的适用性, 从而完善了VG损伤模型、扩展了模型本身的适用范围.

4 结 语

本文进一步解析了层裂实验自由面速度曲线的变化特征与材料内部损伤演化之间的相互关联,并基于自由面速度曲线实验测量结果, 经过理论推导, 给出了VG层裂损伤模型参数的理论标定方法, 相关实验结果的有效模拟验证了方法的适用性, 进而提高了计算结果的可信度. 同时, 本文所采用的技术路线不仅为其他损伤模型参数的确定提供参考, 也有利于层裂损伤模型的进一步完善和发展.