基于Polar WRF模拟结果估算南极泰山站近地面大气折射率结构常数

杨期科 吴晓庆 韩亚娟 青春

(1 中国科学院安徽光学精密机械研究所,中国科学院大气光学重点实验室,安徽 合肥 230031;2 中国科学技术大学研究生院科学岛分院,安徽 合肥 230031)

提要 天文台址的选择与近地面的光学湍流强度密切相关,南极与中低纬度相比,具有极低的天空背景辐射、极低的气溶胶浓度和非常小的光污染,吸引了世界多国在此建立天文观测站。采用专门用于极地研究的极地数值天气预报模式(Polar WRF)来模拟得到南极泰山站的常规气象参数,对于温度和风速大小,模拟值与观测值的相关系数分别高达0.95和0.89。由模拟得到的常规气象参数根据Monin-Obukhov 相似理论估算折射率结构常数并与位于泰山站处移动式极地大气参数测量系统的观测结果做了对比,结果表明模拟值与观测值变化趋势基本一致,相关系数达0.67。

0 引言

地基光学天文望远镜作为光电系统,接收大气中传输的光波,受大气光学湍流影响非常大,会产生光强起伏、到达角起伏、光束扩展等湍流效应,而量度光学湍流强度的量为折射率结构常数与中低纬度相比,南极地区天空背景辐射、气溶胶浓度、大气温度都很低,这些因素使得南极成为地基天文台选址的理想场所,吸引了世界多国在此建立天文观测站[1]。

Qing 等[3-4]运用到的只是标准版WRF,我们这里将采用极地数值天气预报模式(Polar WRF)来计算南极泰山站的。Polar WRF是由美国俄亥俄州立大学(the Ohio State University,OSU)的伯德极地和气候研究中心(Byrd Polar and Climate Research Center,BPRC)开发的专门用于极地地区模拟的区域中尺度天气模式,它是建于标准版WRF 基础之上的,其开发是借鉴Polar MM5[5](fifth-generation Mesoscale Model)在极地的修改经验。Polar WRF 针对极地地区对物理过程的参数化方案做了很多改进,并在格陵兰岛冰盖[6]、北冰洋[7]、北极陆地[8]做了评估工作,通过与观测结果对比,反映出其对极地优异的模拟能力。Polar WRF中的模拟优势部分也逐渐被包含到新版的标准版WRF 当中,如表示海冰和开阔水域比例的分数海冰(fractional sea-ice)也被加到标准版WRF 3.1.1 中,这也缩小了Polar WRF 与标准版WRF的模拟差别[9]。马永锋[10]利用Polar WRF实现对南极多个站点、多个气象参数在表面以及垂直方向的模拟试验研究,反映出其在极地应用的广泛性。Kumar 等[11]使用Polar WRF模拟南极迈特里站(Maitri)区域得到的海面气压和表面风速,对比发现该模拟结果要明显优于印度气象局的全球预报系统。

本文使用Polar WRF模拟结果来计算南极泰山站近地面随时间的变化,通过模式模拟得到地面和2 m 高度处的两层气象参数,再根据Monin-Obukhov 相似理论(MOS),由迭代计算得到。最后将模拟结果与泰山站观测得到的温压湿风以及进行对比分析。

1 现场观测

泰山站是继长城站、中山站、昆仑站之后中国的第4个南极科学考察站,经纬度为76°58′E、73°51′S,海拔高度为2 621 m,该站建成于2014年2月8日。移动式极地大气参数测量系统随中国第30次南极科学考察队到达泰山站,用于南极天文选址,在泰山站建站期间对泰山站的进行测量[2]。该测量系统可以测量0.5 m和2 m 两个高度上的温度、湿度和风速风向,而且在2 m高度上的温度脉动仪还可以同时测量Cn2[12],测量时间为2013年12月30日—2014年2月10日。

我们将大气折射率主要由温度起伏引起的湍流称为光学湍流,并用折射率结构常数来度量。在局地均匀各向同性湍流假定下,对于可见光和近红外光波段,折射率起伏主要是由温度起伏引起的,存在如下关系[13]:

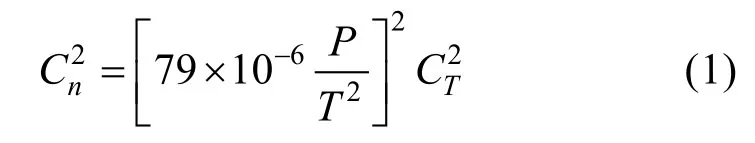
其中P为压强(hPa),T为温度(K),为温度结构常数。

CT2的计算关系式如下:

2 模式参数设置

本文使用的Polar WRF版本是3.9.1,该版本在2017年9月发布。因为模拟整个月的结果,计算耗时非常大,所以这里仅对2014年1月(南极夏季)的月初(1月1—3日)、月中(1月14—16日)、月末(1月29—31日)3个时间段进行模拟,本文的时间是观测数据采用的北京时间(BJT)。高纬度对流层厚度一般比低纬度要薄,有文献使用标准版WRF模拟高纬度近地面湍流时将最高网格分辨率设为0.5 km[4],而对于低纬度则采用3 km[3]。南极的南极点边界层高度平均值在夏季只有三四百米[15],这里模拟南极泰山站区域采用三层网格嵌套,第三层网格分辨率设为0.5 km,母子网格大小比例为5,具体的参数设置见表1。

表1 模拟区域基本参数设置Table1.The basic parameter setting of simulation area

模式地形数据采用美国地质调查局(United States Geological Survey,USGS)提供的24类土地利用数据和30″分辨率的地形高度数据。USGS的24类土地利用信息与卫星传感器MODIS 获取的21类土地利用信息一样,都有冰雪这一类[16],这是南极主要的土地类型。而不同的地形高度数据对模拟结果影响不大,甚至出现精度更高而模拟误差不降反升[17]。

不同学历学员各项考核成绩比较见表2。硕士和学士学位学员各项技能成绩比较显示，腰椎穿刺术、气管插管术成绩比较，差异具有统计学意义[87.0（81.1，92.8） vs.84.3（76.9，87.0），（P=0.047）；87.4（82.5，90.1） vs.81.1（76.2，87.0），（P=0.019）]，其余项目考核成绩比较，差异无统计学意义（P＞0.05）。

模式的初边界条件数据下载使用NCEP 提供的分辨率为1°的再分析资料(FNL)ds0836.2,下载网址为:http://www2.mmm.ucar.edu/wrf/users/download/free_data.html。该分析资料时间分辨率为6 h,每天的开始时间为02:00 (BJT)。

因为南极风暴中心移动比较快,Bromwich 等[18]对南极温压湿风进行模拟时采用较短的模拟时间,为48 h。本文每一次模拟的时间为46 h。南极比中低纬度模式调整适应时间长,即模拟场需要一定的时间才能达到稳定,一般需要将模拟时间的前面 12 h 或者 24 h 作为调整时间(spin-up time)[6,19],即不使用前面一段模拟时间产生的结果。因为使用的FNL 初始场数据不是从每天00:00(BJT) 开始的,为了方便计算,这里模式调整时间设为前面的22 h,而被用于与观测时间做对比的模拟结果则为后面的24 h(=模拟时间46 h–调整时间22 h),即设定模拟计算22 h 之后模式才开始输出结果以供使用。后面图1—3中出现的月初、月中和月末3个时段,每个时段是将3次模拟结果(24 h)的拼接,目的是为了展示较长连续时间的参数变化规律,并不是1次模拟时间长达3天。

WRF 用户手册对于寒冷地区模拟提出参数设置建议,并且设置建议已被应用到南极中尺度预报系统(Antarctic Mesoscale Prediction System,AMPS),AMPS 模拟也是基于Polar WRF 运行。比如垂直层数设置为44层,顶层气压设置为1 000 Pa,对物理过程建议使用的参数化方案见表2,我们在模拟计算前的参数设置时采取了这些建议。该用户手册详见WRF 官方网站:http://www2.mmm.ucar.edu/wrf/users/,其中有对WRF模式的详细说明,可以帮助读者使用WRF。

表2 物理过程参数化方案设置Table2.The physical scheme setting

3.1 近地面计算方法

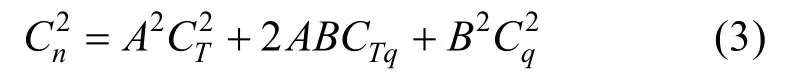
根据Monin-Obukhov 相似理论,可以得到式(3)中的结构常数为:

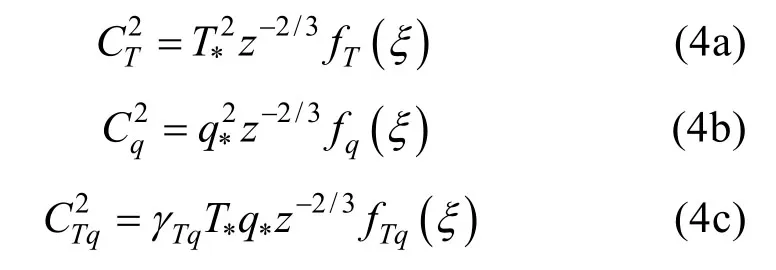
其中,z为离地面高度(m);T*为特征温度,q*为特征湿度;ξ为大气边界层稳定度无量纲参数;γTq为温湿相关系数,当时,当时,为绝对湿度(kg·m–3);和f Tq（ξ）是半经验函数,Edson 与Fairall[21]认为这里采用Wyngaard 等[22]给出的表达式,如下:

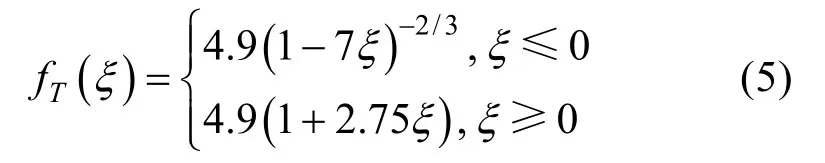
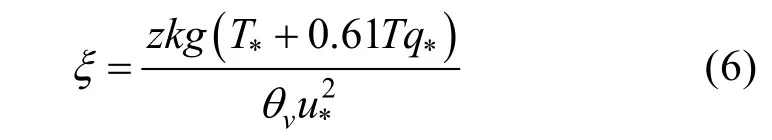
其中,k为卡曼常数(0.4),g为重力加速度(9.8 m·s–2),为虚位温(K),u*为摩擦速度,与特征函数T*、在边界层的表达式如下:

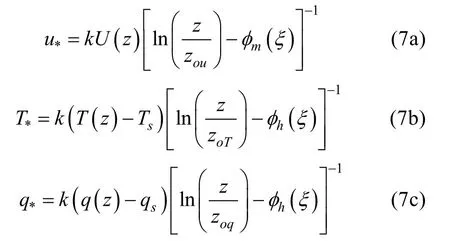
其中,zou、zoT、zoq为粗糙度函数,表示如下[3]:

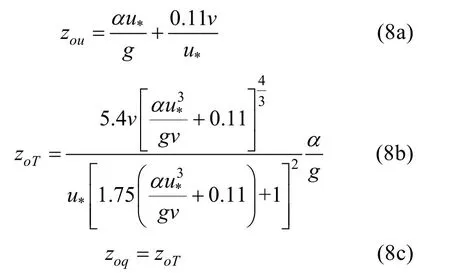
上式中系数α=0.0185,粘滞系数v= 1.7147×10-5m2⋅ s-1(标准大气海拔2 km 处值)。

经验函数φ m（ξ）和φ h（ξ）满足如下关系[20]:

其中,x=（1-16ξ）1/4。

将地面和2 m 高度处的两层气象参数(温压湿风)代入方程式(6)～(9)迭代计算可以得到稳定度函数ξ,特征函数u*、T*、q*,从而可以计算方程式(4)中的结构常数,最终由式(3)得到折射率结构常数。

其中由Polar WRF模拟结果无法直接得到地面相对湿度和地面上2 m 高度处的风速。相对湿度在近地面变化不大[12],本文认为2 m的相对湿度与地面相对湿度一样。而2 m 处风速可以基于对数风速廓线求出[18],因为2 m 高度非常接近地面,按中性情况计算不会引入明显的误差,所以将模拟结果中近地面两层风速代入中性层结下风速廓线的典型形式:

由上式可以拟合得到近地面风速廓线公式,进而由拟合公式得到2 m 高度处风速。

3.2 统计评估方法

其中,和是模拟值和观测值的统计平均。计算统计量时是对其对数值(lg)进行计算。

4 模拟与测量对比

因为计算时我们特意将泰山站设为模拟中心,大致以中心对称方式进行三层网格嵌套,以使得泰山站区域计算网格点最密,最终模拟得到与泰山站最相近的网格点经纬度为:76.973°E、73.853°S,高度为2 624 m,因为该网格点与实际泰山站地理信息很接近,这里就将该网格点的模拟数据直接与泰山站观测数据进行对比。

这里采用NCL(NACR Command Language)读取Polar WRF的输出结果,输出时间间隔为10 min,对应观测值是选取与模拟值时间差最小的(相差都在1 min 以下),并用MATLAB 对读取的结果迭代计算以及绘图(基本上迭代次数达到6次,稳定度参数ξ值误差就都达到1‰以下)。图1给出了温压湿风随时间的变化图,其中温度、相对湿度、风速和风向是在2 m 高度处随时间的变化值,压强是地面压强,压强随高度变化缓慢,计算时用地面压强表示高度2 m 处的压强。2 m 高度处的风速是通过式(10)计算得来的,而风向是直接使用NCL读取的10 m高度处风向,如此得到的风速风向与测量值的相关系数分别高达0.89、0.85(见表3),这也说明采用对数廓线公式计算是很可靠的。

通过图1可以看到,Polar WRF模拟得到的温度起伏要大于观测值;模拟得到的压强值与观测值几乎重合,说明模拟效果非常好;模拟得到的相对湿度在月初出现很大的偏差,而在月中和月末与观测值一样随时间变化平缓,值大小非常接近;模拟得到的风速与观测值的变化趋势一致,只是在风速变大过程中,模拟值会略偏大,这可能与对数风速廓线计算方法有关;而模拟的风向随时间一直在观测值附近波动。

表3给出的是对常规气象参数温压湿风和的统计分析结果,在统计分析前进行数据质量控制,剔除异常数据。从表3中可以看出,常规气象参数模拟值与观测值相关性非常好,相关系数都达到0.85以上,只有相对湿度相关性较低,为0.44。但因为诱发湍流主要是温度梯度和风速切变[24],湿度相对影响较小,所以对数的Rxy也能达到0.67,模拟值相对于观测值平均偏大0.28,RMSE为0.40。也有文献[25]用南极泰山站直接观测的常规气象参数来估算对数的Rxy为0.72,RMSE为0.37,与本文研究结果相近。

表3 观测与模拟在地面上2 m 高度处温度(T),压强(P),相对湿度(RH),风速大小(WS)和风向(WD)的偏差(BIAS),均方根误差(RMSE),相关系数(Rxy)Table3.The bias (BIAS),root-mean-square error (RMSE),correlation coefficient (Rxy) of temperature(T),pressure(P),relative humidity(RH),wind speed(WS) and wind direction(WD) at 2 m above ground between the measured and simulated

5 结论

本文利用Polar WRF模拟得到南极泰山站1月份3个时段的冰雪面上两层常规气象参数。诱发湍流的主要因素是温度梯度和风速切变,本文模拟得到的2 m 高度处温度的Rxy达0.95,而2 m风速大小采用中性层结对数廓线公式拟合计算得到,Rxy高达0.89。

本文是首次尝试用Polar WRF模拟结果来计算泰山站近地面的,结果与观测值基本一致,这说明采用Polar WRF模拟结果为天文观测选址提供参考具有可行性。然而这里仅仅是与1月份夏季观测数据进行对比,Polar WRF 对南极冬季情况模拟可能更好[18],所以下一步可以对南极冬季进行观测以及模拟试验,为南极天文观测应用提供更多的参考价值。

致谢感谢中国南极第30次科考队员对观测系统的安装和维护;感谢美国OSU的BPRC提供的Polar WRF模式;感谢NACR和NCEP提供的FNL分析资料。