氨气传感器响应回复过程模型分析

张文博 吴凯涵 关 茜 李晓红*

（浙江中医药大学，浙江 杭州310053）

1 概述

气体传感器是气体检测系统的关键，从本质上来说，它是一种能通过某种规律（如传感器与待测气体接触时电阻发生变化）将一定浓度的某种气体转化为电信号的器件或装置，从而进行检测、监控、分析、报警[1，2]。

本文选取二房室动力学模型对气体传感器气体浓度随时间的变化规律进行描述，采用最小二乘法优化动力学参数，并得到全局最优解。

2 两房室动力学模型的建立与求解

2.1 吸附和解吸附的工作原理

重复性的第一轮测试的响应阶段中，一定浓度的氨气以恒定速率进入测试腔后，一部分气体从测试腔的另一端导出，部分氨气分子在传感器的表面进行吸附和解吸附。氨气传感器在响应阶段的一级动力学模型如图1 所示。

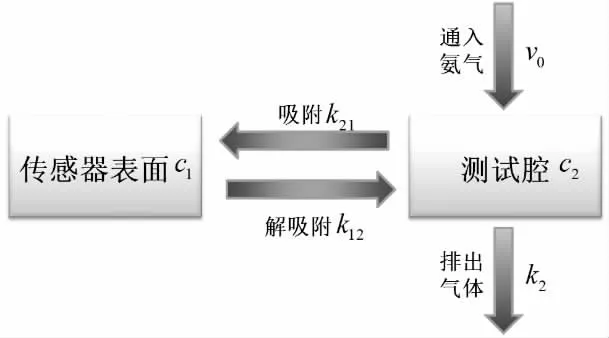
图1 传感器响应阶段动力学模型

图1 中，v0是氨气进入测试腔的速度；

c1是传感器表面氨气分子的浓度，c2是测试腔内氨气分子的浓度；

k21和k12分别是传感器表面氨气分子吸附和解吸附的一级速率常数；

k2是测试腔向外排出氨气的一级速率常数。

而回复阶段氨气流量降为0，因此设c1是传感器表面氨气分子的浓度，c2是测试腔内氨气分子的浓度；

k21和k12分别是传感器表面氨气分子吸附和解吸附的一级速率常数；

k12是测试腔向外排出氨气的一级速率常数。

图2 传感器回复阶段动力学模型

2.2 响应和回复阶段模型的建立

2.2.1 响应阶段二房室模型的建立

基于传感器表面吸附和解吸附的基本原理，在响应阶段，氨气传感器的氨气分子浓度的动力学模型可用下列微分方程组模型描述：

2.2.2 回复阶段二房室模型的建立

根据吸附与解吸附的原理，在回复阶段，氨气传感器表面的氨气分子浓度的动力学模型可用下列微分方程组模型描述：

为了求出模型的全局最优解，需预先设定5 个变量的初始值和取值范围，本文采用二分法，先粗优化，即对150 个至256个点的响应值，带入上述模型，粗优化得到A1，α，D1的值。同理，利用前150 个点的响应值，粗优化得到参数β1，β 的初始值。最后，以得到的五个参数的初值为初始值，在整个相应过程求解全局最优解。

3 求解结果与验证

在响应阶段，求解出的全局最优解A1=-27.22416，B1=-27.18401，D1=55α=0.00126798，β=0.2，即传感器表面氨气分子浓度c1（t）与时间t 的关系为：

4 结论

本文基于气体传感器的原理，参考两房室动力学模型，分别描述了响应阶段和回复阶段气体浓度与时间的定量关系即响应值与时间的关系，采用最小二乘法及lingo 求解出局部最优解，并通过MATLAB 遍历算法和拟合工具箱对局部最优解进行优化。最终结果显示优化后的参数在模型中有较好的拟合优度。

即便如此，模型仍存在一些问题。如响应阶段和回复阶段的吸附速率、解吸附速率、排出速率存在一定的误差及两阶段之间的联系等，还需要进行大量的实验数据挖掘，才可以更好地用于实际生产中。