粒子群算法在优化问题中的应用研究

李树松

（华北电力大学，北京102206）

1 粒子群算法介绍

粒子群优化算法（PSO）是基于鸟类捕食行为的研究，它模拟了自然界中群体间社会行为的仿生优化算法。在粒子群优化算法中，每个粒子都有自己的位置和速度以及优化函数决定的适应值，每个粒子知道本身的最优位置以及整个群体中最优的位置，每一次迭代中粒子通过跟踪两个最优位置进行更新，直至找到最优解。

由于粒子群算法简单易实现，收敛速度快、解质量高、鲁棒性好等优点，因此从出现至今，被迅速应用许多科学和工程领域，目前算法已成为群体智能算法的一个重要分支。

2 粒子群算法的数学描述

粒子群算法的数学描述：粒子搜索所求解问题的D 维空间,种群的大小N, 一般情况下粒子群算法的求解效果随种群规模的增大而变得更好，但同时随着种群的扩大，求解的时间也将随之增加，所以选择合适的种群规模对优化求解问题是十分必要的。

第i 个粒子的坐标可以表示为Xi=（xi1，xi2，…，xid），速度V代表粒子移动的大小，Pbeest=（pi1，pi2，…，pid）为粒子i 迄今为止到达过的最优位置，Pg=（pi1，pi2，…，pid）为整个种群中至今经历过的最优位置，粒子通过如下公式来更新的位置和速度：

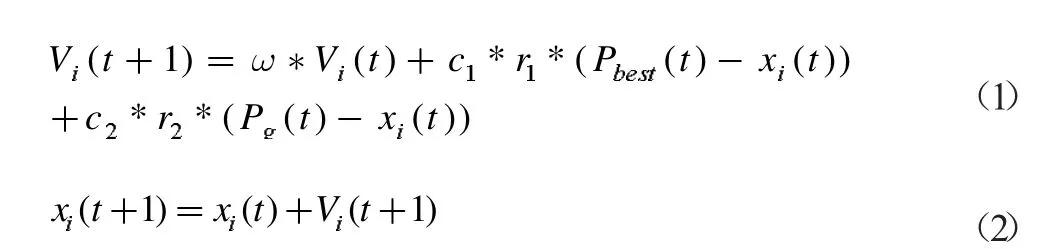
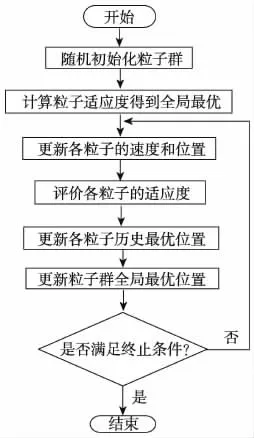
其中，ω 为惯性权重因子，c1、c2代表加速常数，分别为自身经过的最优位置和全局最优位置对速度的影响程度，r1，r2∈[0，1]的随机数，其流程图如图所示。

3 粒子群算法的研究现状

3.1 改进更新策略

文献[1]针对粒子群算法解决流水车间调度问题易陷入局部最优的问题，将模拟退火算法得到的全局最优粒子与粒子群的更新过程相关联，并利用模拟退火算法中温度参数来控制种群的全局最优，增加种群的多样性和求解能力。

文献[2]将随机黑洞策略作为寻优粒子的更新方法,进而扩大粒子搜索区域，并在梯级水电站多目标短期优化调度的应用中验证了改进算法的优越性。

文献[3]针对粒子群算法在电力系统无功优化中“早熟”的问题，提出在速度更新方程中添加二阶振荡环节以提高粒子的多样性的方法，经过MATLAB 仿真表明改进后算法能够快速取得全局最优解，并且网损明显下降。

3.2 学习因子的改进

文献[4]在优化求解二维多阈值α- 型模糊散度的最优阈值中，采用线性递减和线性递增函数对学习因子c1 和c2 进行改进，提高粒子的学习能力，在应用中验证了改进后算法提高了分割精度并节省了时间。

文献[5]提出了一种淘汰粒子群优化算法来优化VSG 系统参数，该算法对种群中适应度值较差的粒子进行淘汰，同时对适应度值不同的粒子采取相匹配的学习因子以加快搜索速度，通过仿真证明该算法更适应于新能源发电系统的并网稳定性。

3.3 惯性权重的改进

文献[6]融合网格搜索法与PSO 算法，提出基于网格搜索法的动态惯性权值，并引入了自适应变异算子和局部搜索能力较强的爬山算法。

对迭代过程中的粒子位置添加了动态扰动，进而提高求解的精准度，在对SVM的核函数参数和误差惩罚参数优化中效果高于其他优化算法。

文献[7]为了平衡粒子整体的搜索能力，Clerc 提出带有压缩因子的粒子群算法对学习因子进行改善，并采用随粒子群优化的目标函数值动态变化的自适应权重避免陷入局部最优，通过对Rastrigin 函数进行测试并与其他算法对比，得到该算法在收敛性和稳定性方面均有改善。

3.4 与其他优化算法的混合

文献[8]将混合粒子群算法用于配电网优化的研究，以网络的有功损失最小为目标函数，提出了引入遗传算法的交叉变异算子的混合粒子群优化算法，通过粒子自身个体极值与群体极值的交叉以及粒子自身的变异来更新粒子位置，从而加快了算法的搜索速度，有效地确定了配电网的最优配置。

文献[9]提出一种基于交叉熵的粒子群优化算法，将交叉熵算法加入到粒子群优化算法更新全局最优值的过程中，加快了粒子的收敛速度，并对进化中的粒子增加高斯扰动以实现粒子重构避免早熟收敛，改进后的算法在复杂多模态函数寻优精度和寻优速度方面均有明显提升。

文献[10]针对粒子分布不均匀的问题，采用中值聚类算法对粒子群进行重组，先利用动态聚类方法把群体分为多个小群体，再采用PSO 算法对下层的小群体进行优化，并针对每个区域执行局部搜索，最后采用布谷鸟算法进行深度寻优。

4 结论

粒子群算法是近几年比较热的话题，相对于优化问题粒子群算法凭借自身优势被迅速应用许多科学和工程领域。但根据现在的研究和发展来看，PSO 算法在实际应用过程中还存在着求解精度不足、收敛速度慢、陷入局部最优等缺陷。还有很多方面需要改善。

近年来，由于人工智能的快速发展，粒子群算法有了更广阔的发展平台。与其他的智能优化算法相比，粒子群算法虽然经历的发展较长，但仍然存在着以下几方面的问题需要进一步的研究：

（1）粒子群算法在初期搜索寻优中收敛速度很快，但在后期却易于陷入局部最优。

（2）粒子群算法对算法的准确性，可行性和计算复杂度没有有效的定量分析方法。

（3）将粒子群算法与神经网络，支持向量机等优化方法相结合，构建新的混合优化算法。