不确定环境下复杂机械装配系统设备维修方法分析

李张斌

（哈尔滨地铁集团有限公司，黑龙江 哈尔滨150000）

在不确定条件下，存在着多种难以预知的因素，比如机械设备的磨损情况和器具堵塞情况都会造成系统的故障，特别是系统中主要的设备的故障，就会给整个设备的发展带来损失。所以要想有效的促进系统的运行，就要防止系统出现长时间工作的情况，防止一个系统的故障连带整个系统出现故障，维修的时候，要从系统缓冲区的库存量与状态为主制定科学的维修计划，提升系统生产的效率。

1 缓冲区库存量与设备维修时机的关系

缓冲区库存量与设备维修时间有着密切的关系，因为该研究具有较强的实际运用价值，也具有较高的理论运用难度，所以许多学者对该种研究感兴趣，并且在实际研究IDE 过程中出现了一些有效成果。在有关研究中，学者将系统状态的有关情况进行量化分析，将主要设备的运行最小成本当作目标函数[1]，从而建立了具有一定区别的模型，根据不同模式找到了最有效的维修办法。有关研究显示，在机械设备的维修中构建一个具有离散变量关系的维修计划模型具有良好的作用，对机械模型的设计和对公式算法的求解，可以让解题的思路更加有序，保证系统维修方法的准确性[2]，这个过程中可以将维修的实际时间和出现故障的水平进行分析，保证故障分析的敏感性和可行性。

由此可见，设备维修中对缓冲库存量的制约对于设备维修方法的制定具有积极的意义，本文中的研究主要考虑的是设备缓冲区与上下各级零部件之间的相互关系，让物体从多种不同的角度考虑维护和运行的价值，进而为设备的维修制定科学的方法。

2 模型表达

2.1 装配系统基本模型和状态分析

本研究的主要研究对象就是缓冲区装备系统，研究中对于装配系统中出现的各种物料短缺和物料堵塞的情况不进行考虑。通常装配系统用M1代表设备，在d1的生产下将产品运送到B1进行储存。M2通过d2生产完成后从缓冲区B1得到工件（d1≥d2）具体的工件运送时间不进行考虑。具体参考图1。

一般而言，设备M1 和M2 使用的时间越长，其使用的效率就会逐渐增大，在对设备进行检查的过程中，可以将其具体分为m+2 个状态，如果设备是新的，就可以用0 表示设备没有任何磨损，通常设备的磨损状况越严重，数值就越高，虽然设备的磨损状况越来越高，但是其仍然可以继续进行工作。m+1 代表设备失效了，此时设备无法进行正常使用，需要立即对其进行检修。

图1 装备系统可靠性框图模型

对设备进行维修的时候，u∈{0，1，2}，u=0，这就充分说明不对设备进行维修，设备还可以进行工作，u=1 说明设备需要做正常的预防检修[3]，u=2 说明设备需要进行故障修理。不管是对设备进行预修还是维修，维修的时间都需要通过几何分布进行控制。如果设备此时处于一种1，2，…，m 的状态，可以进行的维修方式为μ=0，如果此时设备正处于m+1 的情况，维修的办法就是m=2，此时的维修方式就是故障维修。

2.2 可靠性成本函数

在对成本模式进行科学构建的时候，需要把装配系统的可靠成本设定为一种任意的状态，其主要的运行成本为Cij，缓冲区域的成本可以设置为h*x（h 代表的是单位的库存成本，x 是库存量），预防维修成本Cρ，故障的维修成本可以用C∫表示，因此可靠的成本函数可以用CS=Cij+hx+CP+C∫+Ct表示。

如果装配的系统的状态为S=（i，x，j）时，如果需要对设备进行维修，就要充分的考虑设备的停机损失和缓冲库存状况，所以生产的损失成本就可以通过Ct=d1t1+d2t2表示。最关键的是，t1代表M1停止使用的时间，t2表示M2停止使用时间，然后两个设备的生产效率分别可以用d1和d2来进行表示，所以公式可以用CS=Cij+hs+Cp+C∫+（d1t1+d2t2）来表示。设备的预防维修使用时间均可以利用几何的计算办法进行干预，如果设备的修复成功是a，那么修复设备所需要的时间t 的概率可以用p（t）=α（1-α）（t-1）来进行表示。

3 对设备维修的方式进行分析

将（i，z，.j）∈S，那么Can（i，j，x）就可以表示设备维修中对成本的最小预设值，α 可以表示成本因子满足0＜α＜1 的计算范围[4]，如果保证α 计算的准确性，就可以保证Can（i，x，j）在整个运用的过程中，具有一定的收敛性。因此对设备进行维修和使用的时候，设备M1的预防维修成本可以是CP1，修复的成功率可以用α 来表示，设备M2的维修成功率可以用CP2进行表示，修复的几率用b 进行表示，成本可以用C∫2来表示，修复的几率是b'，所以结合上述使用的公式，可以将维修系统中的运行成本进行分类，最佳的成本是系统中可靠成本的最小值，所以可有根据维修状况建立模型：

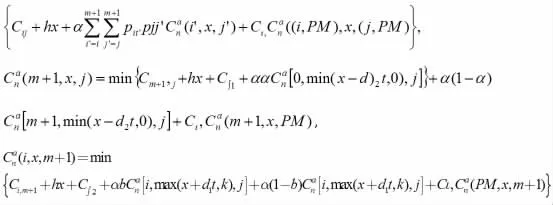
以上公式可以表示，如果机械处于正常的运行状况，就可以通过缩小运行成本来判断有效的预防维修方法，因为在对故障M1进行维修的时候，要判断设备M2是否需要进行预防维修。

4 实例验证

要想保证以上实验中结论的准确性，就要进行实例的验证以上结论的正确性，现给出以下实例进行分析。将汽车离合器盖和压盘的装配线进行综合性的检测，二级装配系统模型与促进机械系统的平衡，在完成检测以后，产品可以通过缓冲区的托盘运送到规定的区域。

具体见图2。

装配系统已经具备的参数有：

m=10，K=5，g=0，那么i 与j∈（0，m）范围内，Cij=0.3（i+j）；如果i=PM 或i=m+1 时，Cij=0.3j；当j=PM 或j=m+1，则Cij=0.3i；Cij=1.8，a=0.98，Cij=2.1，a'=0.95，Cp2=2.1，b=0.96，C∫2=3.0，b'=0.94。

实际使用的遗传参数有，pop-size=20，max_gen=1500.Pc=0.4，Pm=0.1，将这些有效的参数带到公式中进行计算，让其在Matlab7.0 的环境下进行求解，然后算出最后的结果，实际的计算结果如表1 显示。

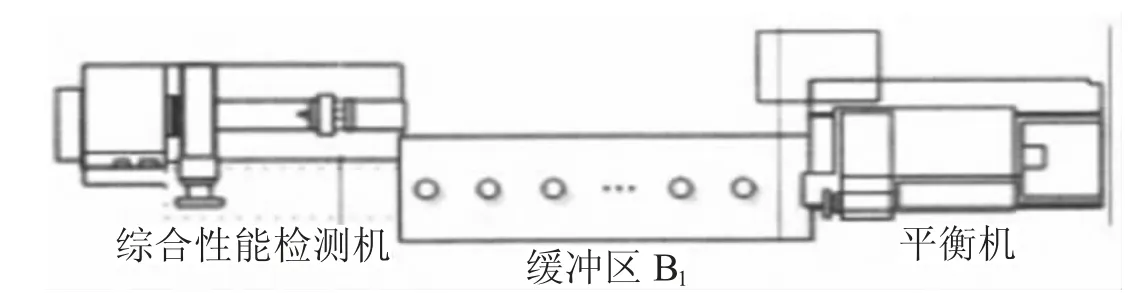
图2 二级装配系统模型

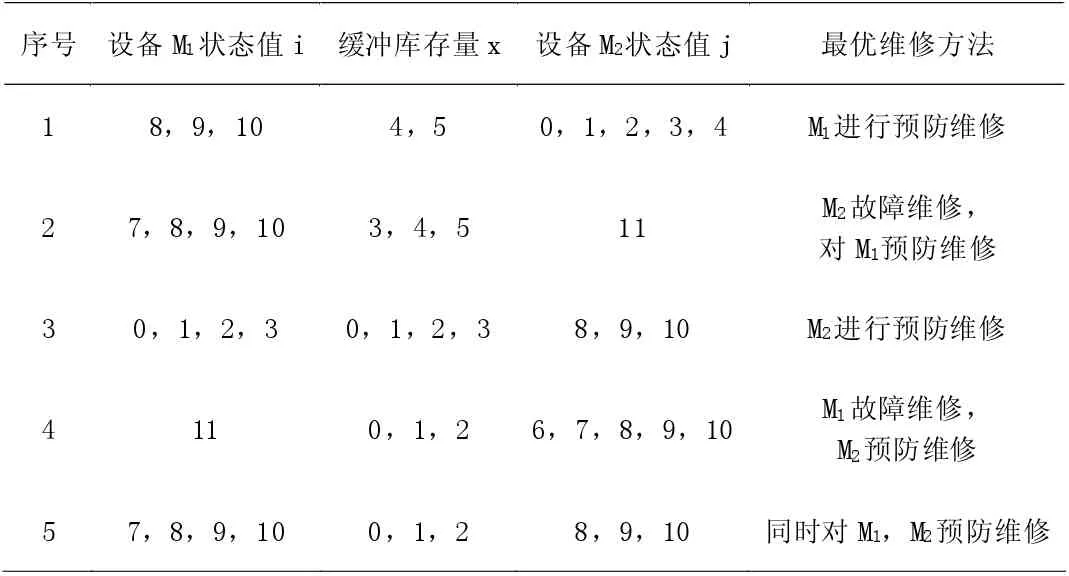
表1 最优维修方法

5 结论

在复杂的环境下，对机械制造系统维修的方法进行分析，需要从机械的实际运用情况出发，充分的考虑系统中检验结果的准确性和有效性，保证系统的运行过程中的成本变化，为机械缓冲区域的系统维修提出有效的方法和方案[5]。而且在实际的机械和系统维修中，要随时的关注的系统的使用期限变化，一旦机械的使用时间超出了规定的年限，设备的安全性就无法进行保证，此时设备就要立即停止使用。

在本研究中通过构建马尔可夫理论的相关模型，对机械维修中的成本进行预算，进而可以详细的将系统维修中不同机械运行状态的有效性成本进行计算。实际的计算分析要从数据的实际情况出发进行分析。

在具体的模型中，主要就是通过遗传算法的相关性将模型中的最佳答案求出来，进而给出最优的维修方案[6]。因为有关研究结果显示，要想做到对实际装配系统的维修，就要使用科学的装配系统维修方法，时刻在维修中分析状态阈值的变化。因为一般来说，对于设备的维修，主要包括两种：一种是大修，一种是小修，但是无论是哪种维修方法，都需要可靠的维修成本最为依据，进而保证维修方法选择和缓冲库存之间的良性变化。本文中的相关研究，对装配系统中的各种维修计划制定具有积极的意义，也为维修工作的成功提供保障。

实际上，建立良好的成本模型能够有效的降低维修成本，让机械的实际运用效率有效的提高，保障生产的价值和生产的连续性属性，实现系统的使用价值。在后续的研究工作中，要重点的关注不确定环境下对于复杂机械装配系统维修方法，考虑实际运用中各种率因子与修复率的变化，保障设备维修的质量。