一阶自由变元tableau 实现过程分析

杨杰

（山西职业技术学院，山西 太原030006）

经典数理逻辑作为数学研究的重要分支，在以数理逻辑为主的证明理论中，一阶逻辑语言成为其实现和证明的重要媒介，因此语言的可靠性和完整性成为逻辑证明的重要评估对象。本文基于经典数理以及相关证明理论来进行一阶自由变元tableau 实现过程分析。据文献目前自动证明（ATP）仍是逻辑证明和推理研究的主要方法，其实现过程基本依赖于归结法和语义Tableau 方法。

因此本文基于M.C.Fitting 研究基础通过改进对应的算法，来进行算法的正确性评估，最后基于实验基础上，通过对比研究，进一步证明改进后的系统算法在推理效率和时间上均优于常规算法[1-2]。

1 一阶逻辑概述

目前，我们熟知的程序设计语言有C 语言、Java 等，这些语言以编程的形式，将语言和程序进行融合来对某个行业、领域进行表达和描述，例如在数学知识表现方面，一般的数学公式、定理以及推理都需要借助一阶逻辑来进行知识的体现和表达，但一般情况下每个性质、定理往往会有不同的性质表达，因此在实际应用中会根据其适用范围来进行语言的选择。

例如在数学定理证明方面，往往需要一个一般意义的符号来表示内在语言，如需要深入讨论内在语言，则需要再继续增加一个元符号来进行语言的表达。因此在考虑语言性质和用途方面，基本对所有的语言都适用，一般语言一般由逻辑符号和知识符号构成[3-4]。

2 一阶逻辑的语义Tableau 方法

目前对于一阶逻辑证明的方式多种多样，一般情况有归结法和语言Tableau 法可以适用，在语义Tableau 系统中，归结法和语义Tableau 法都具有互制性，如要对假设A 进行证明，则需要提出假设A 的矛盾体，在假设过程中来对A 进行证明拓展、验算，其拓展和验算的方式一般是通过树的形式来进行表达，每个节点都是公式。

Tableau 方法就是在树的基础上把树的分支看成公式的假设之一，通过的公式类型可分为ɑ 公式、β 公式、否定公式、λ公式和δ 公式。每种公式相对应的语义Tableau 扩展规则如表1 所示：

表1 Tableau 扩展规则

根据以上Tableau 演变方式，因此对Tableau 概念进行多种定义。

3 一阶自由语义Tableau 系统实现与改进

3.1 Tableau 系统实现

目前大部分的定理证明自动化都会根据语言归结系统来完成，也有一部分是通过Tableau 系统来完成，尤其是随着智能化技术的发展，根据语义Tableau 进行定理、假设的证明已经成为趋势。本文借助一阶自由变元Tableau 系统来进行假设命题等相关的证明，但在运行过程中往往需要额外增加一些限制条件，来进行语言系统的拓展运算。本文就主要步骤来进行具体说明[5-6]：

一阶自由变元Tableau 的实现代码的实现：

目前一阶自由变元Tableau 的实现主要借助remove（_，_，_）等命题来进行逻辑表达，如具体的代码如下：

remove（X，[]，[]）.

remove（X，[Y|Tail]，Newtail）:-

X==Y，remove（X，Tail，Newtail）.

remove（X，[Y|Tail]，[Y|Newtail]）:-

X==Y，remove（X，Tail，Newtail）.

每个运行规则都需要特定的符号来进行表达，如本文通过函数符号f（n）来进行函数符号的表达，n 为正整数，每个规则的n 会增加1 个单元，本文引用符号funcount 来进行函数n 值的标记。程序引入谓语符号reset 来进行n 值的复原，具体实现代码如下所示：

funcount（1）.newfuncount（N）:-funcount（N），

3.2 Tableau 系统改进

为了对Tableau 系统改进，本文通过分析一阶自由语义Tableau 系统实现发现，在语言分支过程中，彼此之间的分支是封闭的，但在对应的谓语词验证中，系统又会对每个Tableau 分支进行检测识别，因此造成效率的降低和重复检测；为了进一步提高程序检测效率，本文基于M.C.Fitting 来对Tableau 进行改良优化，实现对互补程序的单一检测，提高系统分支的检测效率、降低算法的运行空间[7]。

算法TabProver（X）

输入一阶逻辑公式X、

输出如果X 成立，则输入yes，否则no

定理：假设A 为公式、如果A 不是检测对象，则算法结束且结束终止于no；否则，算法止于yes。

证明：假设算法是可以被终止的，设T 为集合中的公式且未被实例化，每个运行后，分支中的T 个数会减少，因为X 是有限的，所以循环会被终止，则该算法结束，假设算法是正确的，那么假设A 不是有效的，但最终止于yes；因此根据循环条件假设A 是有效的，和原假设矛盾，但由于系统止于no，当A 是有效的，但不止于yes，则公式被拓展后，Tableau 分支没有封闭，则A不是有效的，和原假设矛盾，因此算法止于yes。

4 实验对比分析

本文基于Prolog 语言在Windows 下，以一阶自由语义Tableau 系统分别对改进的系统进行典型问题验证并进行对比分析。

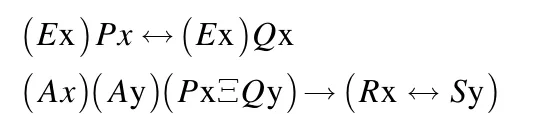
通过实验得出改进优化前的证明该定理所消耗的时间为0.122s，改进优化后所需要的时间为0.015s，运行效率也提高了90%，以同样的方式对10 个问题进行实验，具体结果如表2 和图1 所示。

表2 改进前后时间记录表

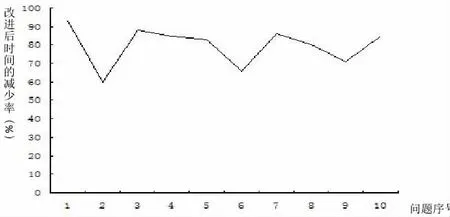
图1 改进前后时间效果对比

从以上图表可以看出，10 个问题运行效率都显著提高，最为表现突出的为问题1、3、4、7、10 等。进一步可得出结论为优化后的系统耗能时间减少了90%，因此改进后的系统TabProver与原系统相比较在运行效率显著提升，证明系统算法优化的必要性。

5 结论

由于目前一阶逻辑自动定理存在一定的缺陷，为有效杜绝由于其缺陷而造成系统运行过程故障。本文逻辑证明和推理研究的研究方法，通过优化改进对应的算法机制，来提高一阶逻辑自动定理的效能和准确度，通过研究表明，优化后的算法在比原有算法运行效率提高了88%且系统具有较强的兼容性，因此可被扩展到非经典逻辑中，可以使此方法应用到不同领域中，从而提高了系统的应用范围。