基于K- Means 与DBSCAN 聚类算法据背景下基于高校综合性数据的学生行为分析与研究

2020-11-05田春子杨德会王勇强孙淑营

科学技术创新 2020年32期

田春子杨万杨德会王勇强孙淑营

（北京交通大学海滨学院，河北黄骅061199）

1 概述

现在人们大都是处在数据化的时代[3]，信息化迅速的发展，同时学校信息化进度也逐渐加快，校园里的信息化规模逐渐的扩大，例如学生存储[3]在学校的校园卡日常消费数据、学期成绩数据、去图书馆借书学习次数、课后上机实验数据等校园活动，这些活动都一直在产生各种类型的数据，例如学生使用校园网产生的网络日志也呈现指数级的增长，因此形成了学校里的大数据状态[3]。

因此怎样更好的利用信息结果去提升学生管理质量和效率，是目前需要特别面对的问题，本文结合数据挖掘算法（K-Means 与DBSCAN）和大数据技术分析学生在校期间产生的多类型数据，从中得出有帮助的、有意义的结果，以便学校工作者更好的管理学生，提高他们的工作效率和服务质量，让学校管理工作人员对学生有更多的了解，让他们在工作时能找到有价值的指导，从而可以为学生提供更好的帮助[3]。

2 算法介绍

聚类与分类有着离不开的关系，分类可以通过划分归类、层次归类、密度、网格、模型法等等来分类。聚类需要具有很多较好的特点：

伸缩性：小于500 这样的数据的处理可能会有较好的表现，但是在上万甚至上百万的数据量下可能出现的结果偏离，所以伸缩性是有必要的。

高纬度：在低维（二维或三维以下）的信息处理下，人们也许可以自己处理很快的处理出来，所以在高纬度的聚类分类是非常复杂的处理，具有高纬度处理也是有必要的。

数据挖掘中会出现的数据量的繁多、具有噪声的、模糊的、随机的，所以在数据量的堆积下分类可能出现一些效应（结果不匹配）。通过聚类算法可以一步步解决，甚至自己可以从分类的结果中发现数据的奇特归类。

聚类算法是数据挖掘常见算法，通过挖掘的数据选定有效值（这里表示属性），计算每个属性的值（维度）对应的距离计算与阈值（分类的标准），距离是数据决定的，阈值可以通过结果去改变慢慢精确。

2.1 K-means 算法

k 均值聚类算法（k-means clustering algorithm）通过迭代分析计算获取局部最优结果，一次次迭代都会使情况趋于稳定（最优）。

算法步骤：初始化目标点，通过计算与相应目标点较近的距离进行归类，每次迭代更新目标点（可以是平均值）。终止条件可以是以下任何一个：

（1）没有（或最小数目）对象被重新分配给不同的目标点。

（2）没有（或最小数目）目标点再发生变化。

（3）误差平方和局部最小[5]。

2.2 DBSCAN 算法

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。通过寻找对应距离（半径内）进行归类，而且归类的集合都是一起的（如果半径没有修改）。

算法步骤：DBSCAN[8]需要二个参数：扫描半径（DR）和最小包含点数（minPts）。任选一个未被访问（unvisited）的点开始，找出与其距离在DR 之内（包括DR）的所有附近点。

如果附近点的数量≥minPts，则当前点与其附近点形成一个簇，并且出发点被标记为已访问(visited)。然后递归，以相同的方法处理该簇内所有未被标记为已访问(visited)的点，从而对簇进行扩展。

如果附近点的数量＜minPts，则该点暂时被标记作为噪声点。

如果簇充分地被扩展，即簇内的所有点被标记为已访问，然后用同样的算法去处理未被访问的点。

3 算法应用与数据分析

K-Means 以属性值计算出距离最近（最优）进行归类，DBSCAN 以属性值计算两点距离是否在阈值范围内以此来归类。与DBSCAN 不同的是DBSCAN 一次性就能出现结果，K-Means 可以通过迭代多次来精确阈值的范围，而DBSCAN 只能通过结果观察去慢慢改变（缺少灵活性），于此同时可以发现DBSCAN 是具有具体的结果数据（稳定结果），K-Means 的随机性较高，最后的结果会有一定偏差（这里的偏差指的是迭代的次数的影响）。K-Means 可以多属性（高维）处理而DBSCAN 不行（这里只能二维），在数据分析中可能K-Means 在多维优势可以体现出来。

3.1 K-Means 算法在学生行为分析中的应用

K-Means 算法在学生行为分析中的应用，在数据集中随机挑选或者自动生成一个参照点（计算距离的样本点），生成的点通常就是分类的个数，每个未被标记访问的数据点，都将与这些生成的参照点进行距离计算，与较近的一个点归为一类，依次对每个未标记访问的点进行计算。

访问一遍之后可以再进行迭代，从每个类里面再次随机生成每个类里面的参照点，迭代次数越多分类变化会渐渐趋于稳定（分类可能不变化）。

K-Means 算法伪代码代码如下：

01：Set＜Cluster＞chooseCenterCluster (){随机选取中心点，构建成中心类。

02：Set＜Cluster＞点空间申请用来放点集合；

03：Random 随机数用来随机选取点的；

04：Point 从点集合中获取随机点使用随机数挑选一个；

05：boolean 用来判断点是否被选取;

06：if (cluster 是否与随机点相同)

07：随机点被使用就标记为false;

10：if (没被标记为false)

11：增加集合点，数量加一；

12：return clusterSet;

13：void cluster(Set＜Cluster＞clusterSet)//为每个点分配一个类

14：float min_dis 距离;

15：两点获取最小距离;

16：if (点距离不同)

17：min_dis 获取当前最小距离;

18：获取点的id;

19：标记当前点的两点间最小距离;

20：新清除原来所有的类中成员。把所有的点，分别加入每个类别

以上代码为K-Means 对点的选取以及分类，介绍了K-Means 的主要思想。用需要先了解算法思想再去看代码可能容易理解。

运行效果图如图1 所示。

以上的效果图可以分析出对应属性的分类情况，这里以canteen 与money 为例的数据分析统计，这里的输出分类以后者的数值为准，所以是money，可以看出87.34（单位为百元）最多（人数），58.50 最少，以大局看来，大部分人花费8734 左右（元）都是比较多，从图中信息看出花费6000-9000 生活费学生数量较多。

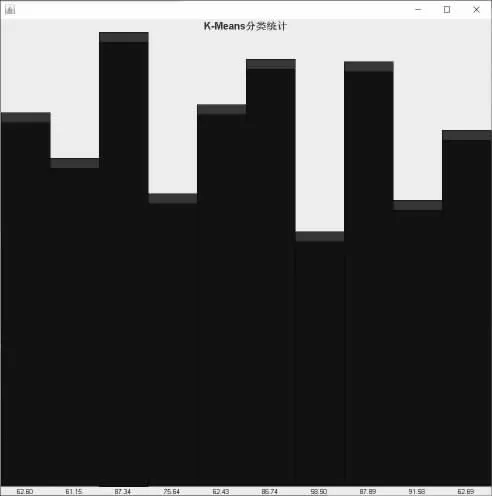
图1 K-Means 分类统计效果图（canteen 与money 属性）

3.2 DBSCN 算法在学生行为分析中的应用

DBSCN 算法在学生行为分析中的应用，通过对数据的计算归类，在数据中初始化一个点（数据随机提取）作为本次迭代的起始点，并将其加入到数据集中；将取到的数据心点从未访问样本集合中标记为已使用；只要数据集不为空集，那么每次从其中提取出首个数据点，如果该数据点为起始对象，那么就将同时存在在该起始对象的数据集中的所有点和未访问集合中的点记录到数据集中，并且从中标记这些点；找到数据中所有的点后，集合数目增一，然后将那些出现在未访问的集合原始拷贝中，且未出现在当前未访问集合的点集合作为本次迭代生成的集合，最后从起始对象集合中标记出现的数据点；当不满足迭代条件时，结束数据点访问，继续访问其他未访问的数据点。

DBSCAN 算法代码如下：

室内环境中VOCs的来源是多种多样的。木材在室内，无论是木梁和柱材的实木形式，或作为工程产品人造板、地板或家具，都会排放VOCs。

01：private void densityConnected(double[][])

02：boolean;//是否已经归为某个类

03：boolean 标记为false;//是不是core 的"邻居"

04：移除点//对某个core 点处理后就从core 集中去掉

05：for(point 遍历点集合)

06：Isneighbour 标记为false;

07：isputToCluster 标记为false;

09：if cluster 是否与随机点相同))//如果已经归为某个类

10：随机点被使用就标记为true;

11：break;

12：if(没被标记为false)

13：continue;//已在聚类中，跳过，不处理

14：if(点的邻居)//是目前加入的core 点的"邻居"吗？，ture的话，就和这个core 加入一个类

15：添加该点

16：isneighbour 标记为true;

17：if (是邻居)// 如果是邻居，才会接下来对邻居进行densityConnected 处理，否则，结束这个core 点的处理

18：if(cores.contains(points[i]))

19：移除该点

以上代码为DBSCAN 对点的分类，介绍了DBSCAN 的主要思想。用需要先了解算法思想再去看代码可能容易理解。

运行效果图如图2 所示。

以上的效果图可以分析出对应属性的分类情况，这里以canteen 与money 为例的数据分析统计，这里的输出分类以后者的数值为准，所以是money，可以看出74.69（单位为百元）最多（人数），从图中信息看出花费6400-8300（元）生活费学生数量较多，结合刚刚K-means 分析的结果可以看出7500 左右的花费占主要，所以可以结合学生个人情况去建议学生每学期的花费使用（增加生活费或者减少生活费）。