管线钢裂纹尖端应力应变状态判断参数探讨

张 华，何浩华，张 宏，赵新伟

(1. 中国石油集团石油管工程技术研究院 陕西 西安 710077； 2.长庆油田物资供应处(物资管理部) 陕西 西安 710016；3. 中国石油大学(北京) 北京 102249)

0 引 言

对于受载的裂纹体，应力强度因子KI是描述裂纹尖端应力场强弱的力学参量。断裂韧性KC或KIC是材料本身的固有属性，两者不同点在于KC是平面应力状态下的断裂韧性。当厚度大于一个临界值后，裂纹尖端就处于平面应变状态，此时断裂韧性就基本不再随厚度的增加而变化，此时断裂韧性表征为KIC[1-2]。

由于裂纹尖端进入平面应变状态后，材料的临界断裂韧性会显著降低，相同尺寸的裂纹在厚度较厚时更容易起裂，对管道的安全会造成极大的威胁。因此随着我国管道建设朝着高钢级、大管径、大壁厚的方向发展，已经大规模应用的高钢级管线钢断裂韧性是否达到平面应变状态，对管道安全运行是否会带来重要的影响，已经受到业界专家的关注。

文献[3]针对X80管线钢，通过不同厚度的断裂韧性试验， 建立平面应变断裂韧性的估算模型。本文在此基础上，进一步分析试验断口，探讨采用裂纹前沿扩展宽度判断裂纹尖端应变状态的可行性。

1 裂纹尖端应力应变场分析

在加载应力后，裂纹尖端的应力状态和塑性区尺寸是相互影响的。应力大小决定了塑性区的大小，但是当裂纹尖端材料发生屈服之后，附近的材料就会随着变形，缓和应力集中。当塑性区的半径和试样厚度相当时，在材料的厚度方向上可以自由屈服。当试样厚度增加，在厚度方向的中心部位，塑性区半径较小，厚度方向上由于周围材料的约束不能自由变形，使得厚度方向的应变很小，试样的厚度表面为自由表面。大多数试样处于中间状态，在试样中心部位为平面应变状态，而在试样的表面为平面应力状态。KC向KIC转变的过程正是由于两种状态在试样厚度上所控制比例的不同导致的。

文献[4]提出，以x为平面应变区宽度，x占试样壁厚的比例是一个重要的参数，如图1所示，随着该比例升高到100%，KC逐步趋向于KIC。

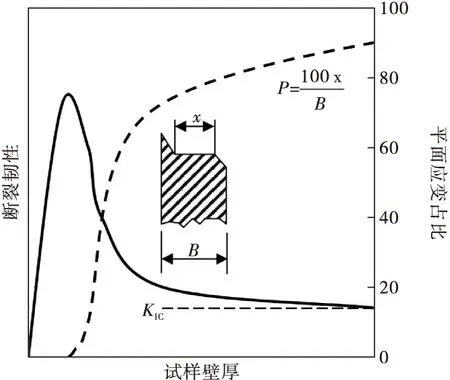
图1 平面应变区比例随厚度变化示意图

2 X80管材断口分析

在进行断裂韧性试验时，在试样断口中部有一舌状裂纹扩展区，其形状如图2所示。图2中，B为试样原厚度，A为试验过程中裂纹扩展的宽度。这是由于裂纹扩展时并不是裂纹尖端同时向前扩展，而是在中心部位扩展最快，试样表面的位置扩展速度较慢。通过裂纹尖端应力应变场的分析可知，由于在试样中心部位，试样受三向拉应力，属于平面应变状态，塑性变形发展受到限制，临界断裂韧性值较低，导致中心部位首先断裂。随着载荷加大，达到临界断裂强度的裂纹尖端宽度越来越大，但中心部位的裂纹扩展速度最快，因此裂纹的扩展形貌类似一个“舌状”。

图2 断裂韧性试样的舌状扩展

对X80和X100管材试样裂纹扩展宽度(图2中的A值)进行了分析，结果见表1和表2。通过测量试样中心裂纹扩展宽度，再除以试样厚度可以发现，在试样大于14 mm之后，随着壁厚的增加，裂纹扩展宽度占试样厚度的比值逐步提高，且呈现线性规律，结果如图3中数据点。

表1 X80裂纹扩展宽度分析

从图3可以看出，当试样厚度超过14 mm时，随着壁厚的增加，裂纹扩展宽度和试样厚度的比值与试样壁厚基本呈线性关系。壁厚小于14 mm时，试样厚度与该比值没有明确的对应关系，这与小壁厚试样中平面应变所占比例较小有关，在小壁厚试样中，平面应力占主导地位，从而导致裂纹扩展的规律和平面应变状态下的裂纹扩展规律有所差异。因此，选取X80和X100管材断裂韧性试验中，壁厚超过14 mm以上的数据点采用线性关系拟合裂纹扩展宽度和试样厚度的比值(A/B)与试样壁厚的关系，如图3所示。以100%作为试样处于平面应变状态的准则，得到X80管线钢试样处于完全平面应变状态的临界壁厚是45 mm，X100管线钢试样的临界壁厚是38.7 mm。

表2 X100裂纹扩展宽度分析

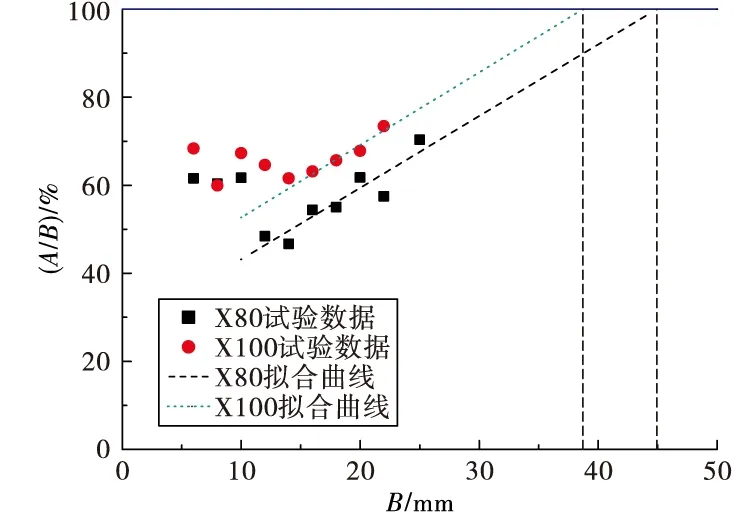
图3 裂纹扩展宽度/试样厚度比值与试样厚度关系

文献[3]建立了平面应变断裂韧性和临界壁厚关系经验模型，通过该模型计算得到的临界壁厚为48.7 mm，两者相差2.7 mm，基本接近。采用上述方法确定临界壁厚，在拟合时都采用了最简单的线性拟合。从前述的分析可以看出，在壁厚逐步增大的情况下，断裂韧性与试样壁厚是一个非线性的递减关系，逐步接近平面断裂韧性值。因此实际的临界壁厚要大于计算得到的壁厚，而计算得到的平面应变断裂韧性可能更接近真实值。另外采用裂纹扩展宽度作为平面应变区的判断依据只是为了提供一个经验性临界壁厚计算方法，而在实际的应力应变场中，可能只有部分裂纹扩展宽度完全达到平面应变状态，且比值A/B趋近1的过程是一个非线性的过程，因此需要在该比值上增加一个0～1之间的系数。

因此，如果将裂纹扩展宽度作为平面应变区宽度的宏观判断依据，在裂纹扩展宽度与试样壁厚的比值达到100%时，则试样完全处于平面应变状态，当然这种情况无法达到，但当该比值高于一定值时，则可以认为试样是处于完全平面应变状态。从前述的分析结果来看，作为判断依据是可行的。

3 裂纹尖端场厚度效应理论分析

三维应力应变场与对材料的断裂影响至关重要，应力应变场又受到离面应力约束的影响[5]。为了更好地表征裂纹尖端的三轴应力约束，离面约束因子被用来描述应力在裂纹尖端厚度方向的分布，其定义为式(1)：

(1)

式中：σ11，σ22，σ33为裂裂前端三个方向的主应力，其中σ33为穿透裂纹厚度方向的应力，σ11，σ22为裂纹前沿法平面上的应力。

对于I型穿透裂纹，Tz在裂纹的中部值最大，在裂纹前沿随着与裂尖距离的增大会很快下降。在距裂纹尖端相同距离处，由试样中心到试样表面，Tz逐渐减小，但在试样中心变化较小，在接近试样表面时，Tz迅速降低直至为零。在线弹性情况下，Tz的取值在0～0.3(弹性泊松比v)之间，对于弹塑性的情况，Tz取值在0～0.5(弹塑性泊松比vep)之间。当裂纹尖端处于平面应力状态时，Tz=0，在平面应变状态下，Tz的取值为vep[5-7]，在0.3～0.5之间。

对于Tz的表达，式(1)只是定义，目前尚无理论上的解析表达式。文献[8,9]根据有限元计算结果提出了针对I型穿透裂纹的拟合表达式：

(2)

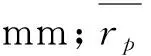
采用式(2)计算裂纹尖端的离面约束因子，结果如图4所示，图中横坐标是沿壁厚方向上坐标与试样壁厚的比值。可以看出，在裂纹的中心部位，离面约束因子基本保持不变。随着壁厚的增加超过某一定值，离面约束因子逐渐降低，到试样的自由表面降为0。不同壁厚的试样，裂纹尖端的离面约束因子分布有所差异。壁厚越小，离面约束因子下降得越早。试样越厚，下降得越迟，说明较厚的试样，离面约束控制的厚度比例越大。另一方面，靠近试样中部，离面约束因子基本保持不变，基本上与裂纹中部的约束因子值相同，由于不同的壁厚，在裂纹中部都处于平面应变状态，因此可以判断，在离面约束因子没有明显下降的区域，已经处在平面应变状态。

图4 裂尖离面约束因子的分布

离面约束因子大于0.3，表明试样已经进入平面应变状态[7,10]。若以离面约束因子值为0.3作为裂纹前沿进入平面应变状态的判据，通过式(2)进行计算，得到不同壁厚试样前沿离面约束降到0.3的z值，求得其与壁厚的百分比，如图5所示。随着壁厚的增加，离面约束因子大于0.3的区域占壁厚的比值逐渐增大。

若以2z/B为0.95为试样完全作为进入平面应变状态的判据，那么实际的临界壁厚应该比48.7 mm稍大。在之前的分析和图5中可以看出，当壁厚大于48.7，所得到的临界平面应变断裂韧性变化已经不大，48.7 mm壁厚试样，离面约束因子大于0.3的宽度与试样宽度的比值为93.4%，100 mm的试样，对应比值为95.7%，变化已经很小。

可以看出，以裂纹前端扩展宽度与试样厚度的比值作为裂纹前沿应力应变状态的直观的判断依据，在与试验结果和理论分析的结果对比来看都比较吻合，具有一定的合理性。通过该参数的表征，可以简单直观的判断试样裂纹前沿的应力应变状态。

图5 平面应变区域宽度与试样壁厚的比值

4 结 论

离面约束是造成三维裂纹尖端应力应变场与二维裂纹尖端状态差异的根本原因，也是造成断裂韧性厚度效应的最根本原因。本文提出以裂纹扩展宽度与试样厚度比值作为试样进入平面应变状态的判断参数，该比值与离面约束因子的变化规律一致，能够反映厚度带来的离面约束效应，对平面应变临界壁厚的预测与经验模型的结果也较为接近，因此该比值作为试样进入平面应变状态的判断依据具有一定的合理性。