有限体积法在采空区自然发火数学模型中的应用
2020-11-05王月红蒋冀萍
王月红,蒋冀萍
(华北理工大学 矿业工程学院,河北 唐山 063210)
0 引言
采空区自燃是采空区经常发生的一种现象,尤其是发生在距采空区有一定间隔的氧化升温带中,采空区分为冷却带、氧化升温带和窒息带,氧化升温带的后面便是窒息带,窒息带内不发生自燃,因此只选取部分区域对采空区自燃进行研究即可。为了简化计算,根据采空区不断变化移动的特点,该项研究在模型中引入了移动坐标系的概念,使得采空区自然发火模型由静坐标下移动边界的非稳态的偏微分方程组变成了移动坐标下边界固定的稳态的偏微分方程组,在很大程度上简化了采空区自然发火三维数学模型的求解。影响采空区自然发火的主要因素有采空区内的风流状况、氧气浓度和温度,而其中的温度又分为遗煤温度和气体温度,因此该项研究分别对采空区内流场、氧浓度场、遗煤温度场和气体温度场进行了分析和相关数学模型的推导,分别建立了采空区流场模型、氧浓度场模型和温度场模型,通过3个模型的耦合求解来建立采空区自然发火模型。
1 采空区流场模型
基于有限体积法“守恒性”的思想,建立采空区流场模型。有限体积法强调从物理角度建立离散方程,在进行推导的过程中物理概念清晰,离散方程的系数均具有一定的物理意义,每个离散方程均为有限体积法中的某个物理量守恒的表达式,并且从物理角度建立方程可以保证该方程具有“守恒性”。有限体积法的优势在于其一方面不仅具有有限元方法的“灵敏性”,而且适用于处理复杂的范围以及边界问题;另一方面,有限体积法采用显示算法,具有更加灵活的假设,可以克服泰勒展开离散的缺点,并且可以很好地解决复杂的工程问题。
1.1 达西定律
达西定律是基于有限体积法思想和质量守恒方程,在采空区内任取一个空间六面体微元,在空间六面体微元中任取一点来考察采空区漏风流的三维流态。有如下关系:
(1)
式中:ux、uy、uz分别为坐标轴3个方向上的速度分量;Kx、Ky、Kz分别为3个方向上的渗透系数;∂p/∂x、∂p/∂Y、∂p/∂Z分别为每个方向上的压力梯度。
1.2 流场控制方程
假设有一流场,取流场内的某一点,该点被如图1所示的六面微元体包围,坐标轴正向为已知。
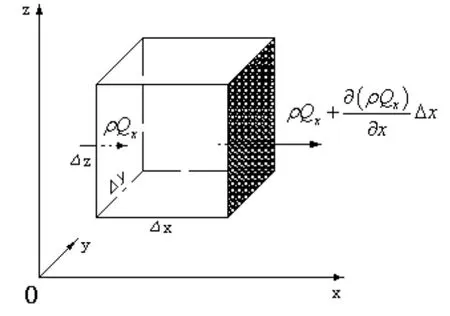
图1 采空区内的某一六面微元体
单位时间内风流流进采空区、流出采空区导致的质量差如式(2)所示。
(2)
单位时间内风流流入控制体与流出控制体的差值和微元体内质量的增加量应该是相等的,如式(3)所示。
(3)
1.3 边界条件
采空区的流场区域及边界如图2所示,Γ1、Γ2、Γ3、Γ4为采空区靠近进风侧的面,Γ5和Γ6分别为底板和顶板。
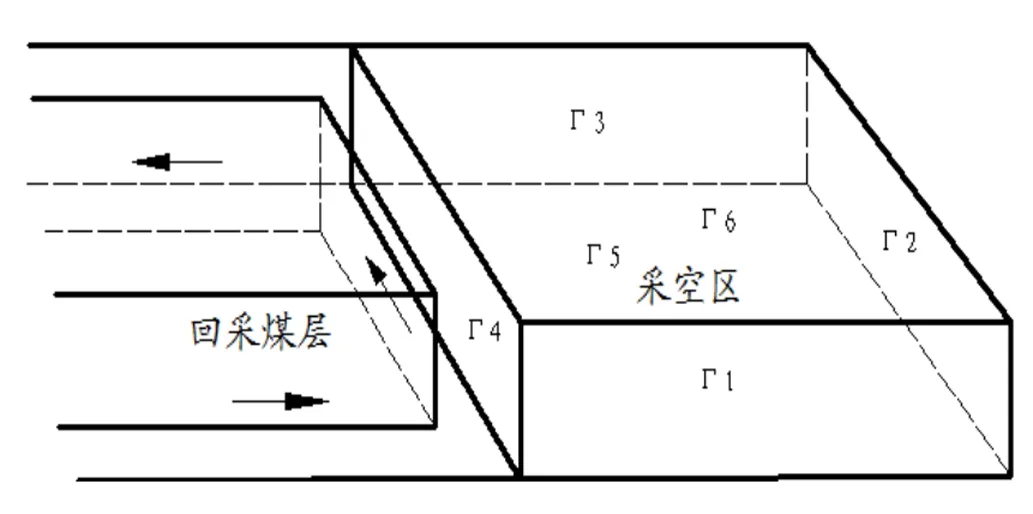
图2 采空区的流场区域及边界
采空区靠近工作面边界的压力值可以测定,因此可表示为如式(4)所示。
P(x,y,z)|Γ4=p0(x,y,z)|(x,y,z)∈Γ4
(4)
式中:Γ4为已知边界;P0(x,y,z)为已知渗流边界上的风压函数。
则流场模型可表示为:
(5)
2 采空区氧浓度场模型
2.1 Fick定律
Fick定律描述扩散作用,可以使用这条定律来求得扩散系数,该定律是由德国科学家阿道夫·菲克于1855年推导出来的。
(6)
式中:J为扩散通量,mol/(m2·s);D为扩散系数或扩散度,m2/s;∂为浓度,mol/m3;x为位置长度,m。
2.2 采空区氧浓度场模型
对采空区内任取的某一六面微元体进行质量守恒分析,在单位时间内,微元体内部的氧气质量变化量(WC)主要由以下3个方面构成:(1)采空区风流流入微元体和流出微元体的氧气质量差值(W1);(2)氧气消耗量(W2);(3)浓度差异引起的流入微元体和流出微元体的氧气质量之差(W3),即:
WC=W1+W2+W3
(7)
其中:
(8)
(9)
(10)
(11)
将式(8)、(9)、(10)以及(11)代入(12)得:
(12)
为了便于计算,将式(12)中质量浓度改为摩尔浓度,即为式(13)。
(13)
2.3 边界条件
采空区的氧浓度场区域及边界如图3所示,共有Γ1、Γ2、Γ3、Γ4、Γ5、Γ66个面的边界。
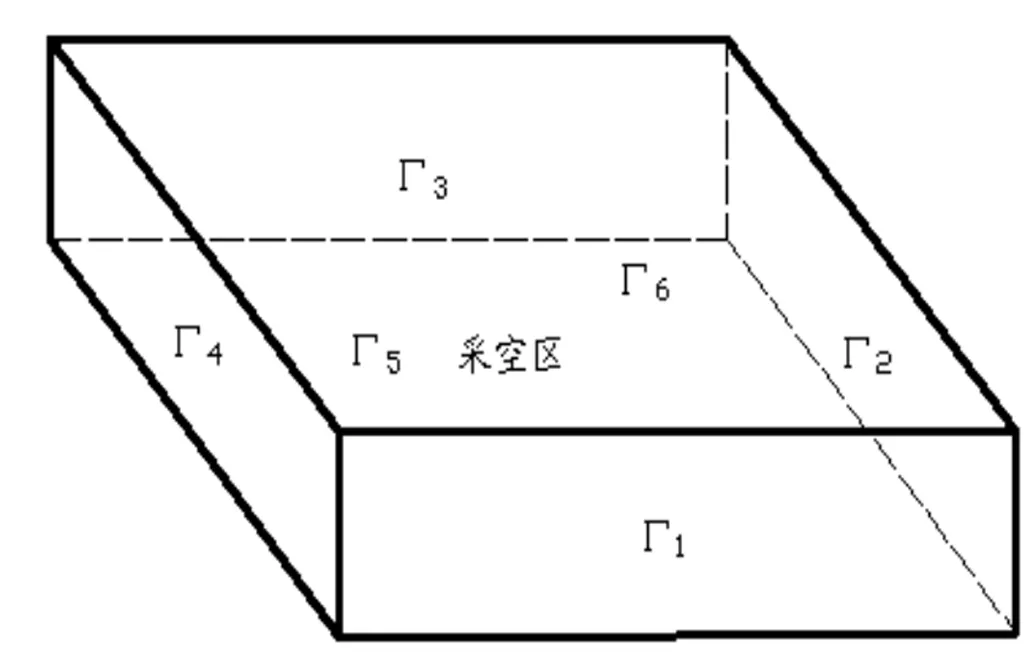
图3 采空区的氧浓度场区域及边界
在实际的处理中,只有在工作面附近的Γ4边界可以直接测量,因此对于进风侧可以直接考虑空气中的氧浓度;对于回风侧,考虑到消耗氧气的因素,需要对氧浓度进行实际的测量,但在该项研究中,回风侧处的边界根据第二类边界条件处理,也就是垂直于工作面方向的氧浓度变化是零,如式(14)所示。
(14)
采空区内进风侧和回风侧,即Γ1边界和Γ3边界的耗氧量几乎可以不计,所以在该方向上的氧浓度变化率为零,因此可根据第二类边界条件进行处理,对于采空区的深部边界(Γ2边界)和上下边界(Γ5、Γ6边界),同理根据第二类边界条件处理,如式(15)所示。
(15)
即采空区氧浓度场模型如(16)所示。
(16)
3 采空区温度场模型
由于难以直接、准确地判断采空区的着火点位置和自燃环境的火情,因此在工程实践中,采空区的防火、灭火工作不仅相对盲目,而且还浪费了大量的人力物力。近几年,随着综采放顶煤技术的推广应用,大大提高了生产效率,但同时也导致采空区内遗煤量更多、漏风更加严重的结果,因此对采空区内温度场进行立体模型公式推导时,将温度场分为遗煤温度场和气体温度场,为及时预测以及研究采空区自燃问题提供了有效直观的研究方法。
3.1 傅里叶定律
傅里叶定律是在1822年被法国著名科学家傅里叶提出的一条热力学定律。表达式如式(17)所示。
(17)
式中:JT为热流密度,w/m2;k为热导率,w/(m·k);dT/dx为该方向上的温度梯度。
3.2 温度场模型
3.2.1 采空区遗煤温度场模型
对采空区放顶煤岩中小型控制体的热平衡进行分析,得到如式(18)所示的守恒方程。
Qsc+Qf-Qd=Es
(18)
式中:Qsc表示由于导热导致的热量差,kJ/(mol·s);Qf表示由内热源导致的热量,kJ/(mol·s);Qd表示由对流换热导致的热量差,kJ/(mol·s);Es表示由工作面移动导致的进出控制体的热量差,kJ/(mol·s)。
其中:
(19)
(20)
(21)
(22)
将式(19)、(20)、(21)、(22)代入式(18)中即可得到如式(23)所示的采空区内固体颗粒的热平衡方程。
(23)
式中:ts表示冒落煤岩温度,K;tg表示气体温度,K;λs表示固体导热系数,W/m·K;Ke表示对流换热系数,J/(m2·s·K);q(t)表示单位时间单位体积的煤氧化放热强度,kJ/(m3·s);Cs表示固体比热容,kJ/(kg·K);v0表示工作面推进速度,m/d;ρs表示固体密度,kg/m3;Sn表示单元体内固体颗粒与气体对流换热的表面积,m2。
3.2.2 采空区气体温度场模型
同理,对采空区中的任一气体控制体进行热平衡分析,可得如式(24)所示的能量守恒方程。
Qgc-Qh+Qd=0
(24)
式中:Qd表示单位时间内由固体与孔隙中气体导致的对流换热量,kJ/(mol·s);Qh表示单位时间内由气体流动带进和带出导致的热量差,kJ/(mol·s);Qgc表示单位时间内由导热流进和流出控制体导致的热量差,kJ/(mol·s)。
其中:
(25)
(26)
(27)
将式(25)、(26)、(27)代入(24)得:
(28)
式中:λg表示气体导热系数,W/m·K;cg表示气体比热容,J/(kg·K);ρg表示气体密度,kg/m3。
3.3 边界条件
采空区温度场模型的边界条件和采空区氧浓度场的边界条件相似,如图3所示,由于采空区温度场的温度可以直接测定,因此对于临近工作面进风侧的边界条件根据第一类边界条件进行处理,表达式如式(29)所示。
(29)
对于采空区的其它边界,可认为在该边界坐标轴方向上的温度没有发生变化,表达式如式(30)所示。
(30)
将偏微分方程、采空区遗煤温度场边界条件和气体温度场边界条件进行整合,可得到采空区温度场数学模型,表达式如式(31)所示。
(31)
4 采空区自然发火三维数学模型
4.1 采空区自然发火三维数学模型
将式(5)、(16)、(31)进行联立得移动坐标下采空区自然发火三维数学模型:
(32)
4.2 边界条件
采空区自然发火三维数学模型的边界条件如式(33)所示。
(33)
将偏微分方程与采空区流场、氧浓度场、以及温度场的边界条件相结合,可以得到完整的采空区自然发火三维数学模型,该数学模型的优势不仅在于从能量守恒的角度建立,具有明确的物理意义,而且还能能准确地描述采空区自燃的过程,为采空区自燃的防治提供了理论依据。
5 结论
(1)根据工作面不断移动的特点,建立了移动坐标系,使得采空区自然发火模型由静坐标下移动边界的非稳态的偏微分方程组变成了移动坐标下边界固定的稳态的偏微分方程组,在很大程度上简化了采空区自然发火三维数学模型的求解。
(2)基于有限体积法“守恒性”思想,利用气体流动规律和达西定律,建立了采空区流场模型,描述了采空区内部压力和风流速度的分布情况;根据氧气扩散规律和质量守恒定律,建立了采空区氧浓度场模型,描述了采空区内部氧浓度的分布情况;根据热传导规律和傅里叶定律,建立了采空区气体温度场模型和采空区遗煤温度场模型,描述了采空区内部温度的分布情况,为采空区自然发火研究提供了理论依据。
(3)采空区自然发火模型是由采空区流场模型、氧浓度场模型、以及温度场模型进行耦合求解来建立的,采空区的气体压力、氧气浓度和温度分布情况在不同程度上对采空区自然发火都具有一定的影响,采空区自然发火模型的建立为采空区内不同参数影响的判断提供了理论依据。
