综合孔径干涉辐射计中模数转换信噪比约束分析方法
2020-11-05杨保华邹华杰程志华
杨保华,邹华杰,程志华
(1.常州机电职业技术学院,江苏 常州 213164;2.常州市工业互联网数据智能技术重点实验室,江苏 常州 213164;3. 江苏省物联网与制造业信息化工程技术研究中心,江苏 常州 213164;4.天津理工大学电气电子工程学院,天津 300384)
0 引言
鉴于干涉式综合孔径微波辐射计在稀疏天线阵列,以及无需机械扫描即可宽视场高分辨率快速成像等方面的优势,从20世纪80年代末ESTAR研制成功开始,一些典型系统如MIRAS[1-2]、AMIRAS[3]、HUT[4]、GEO-STAR[5]和BHU-2D[6]等等相继经过实验验证,并广泛应用于土壤湿度、海洋盐度和人体安检等。在这些系统中可视度不确定度对成像性能至关重要,1位/2阶数字相关器被运用于对中频信号进行数字相关运算[3,7]。而在进行数字相关运算之前,其中频频率信号必须通过模数转换器(ADC)进行数字化转换,这一过程会导致辐射SNR下降[8-9],常用的ADC SNR均方根(RMS)合成方法没有分析输入噪声、量化噪声和采样抖动对可视度不确定度造成的影响。
本文针对此问题,提出了综合孔径干涉辐射计中模数转换SNR约束分析方法,给出了关于输入噪声、量化噪声和采样抖动导致系统SNR下降的系统分析方法。
1 原理及指标
1.1 综合孔径辐射计原理
SAIR成像仪采用毫米波下变频和中频双边带IQ解调的模拟接收机结构,在IQ解调获得基带信号后通过ADC实现实时功率测量,因此ADC的噪声会对可视度不确定度产生恶化。单个接收机通道的电气原理框图如图1所示。
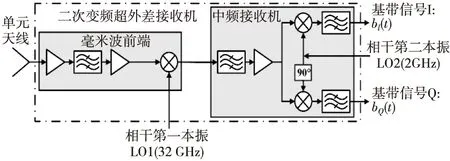
图1 SAIR辐射计每通道接收机电气原理框图Fig.1 The electrical block diagram of each receiver channel of SAIR
考虑到每通道基带信号均需要进行量化后才能进行数字相关运算,量化结构是连接模拟二次变频超外差接收机和数字处理机系统的纽带,其功能原理框图如图2所示。经过中频I/Q解调得到的基带信号必须经过数字量化才能进行数字相关运算、可视度校正和亮温图像反演。在此首先基于条纹洗涤幅度误差理论对数字参考时钟设计约束条件进行分析,随后给出高阶和低阶量化的典型结构,形成具有不同基线的二元干涉仪。
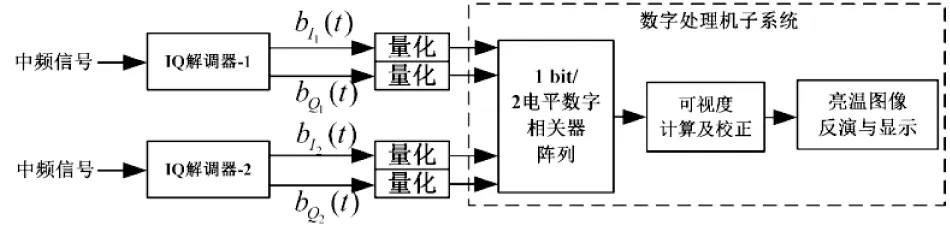
图2 SAIR辐射计双通道量化数字相关原理框图Fig.2 A two-channel demonstrator model of SAIR digital correlation
SAIR成像系统利用稀疏天线阵列和复相关接收技术,将天线阵列中单元天线两两组合,形成具有不同基线的二元干涉仪,测量目标场景的空间频域信息-可视度函数[9],如图1所示。接收信号通过IQ解调后为中频信号,表达式为:
bI1,2(t)=AI1,2(t)exp[jφI1,2(t)]
(1)
bQ1,2(t)=AQ1,2(t)exp[jφQ1,2(t)]
(2)
式(1)、式(2)中:bI1,2(t)代表第1,2个干涉通道的同相基带解调信号;AI1,2(t)及AQ1,2(t)分别代表信号经正交解调后I与Q正交两项的复幅度项;φI1,2(t)及φQ1,2(t)代表信号经正交解调后I与Q正交两项的的复相位项。
中频IF信号对的可视度样本的时间平均可以表示为:
(3)
式(3)中:E[·]表示期望算子,*表示共轭信号,Vij(t) 表示可视度,bi,j(t) 表示经I/Q解调后的中频IF信号,(u,v)表示基线。
根据范希特-泽尼克(Van Cittert-Zernike)定理,可通过对可视度进行校准和反演重建场景亮温图像,表达式为:
(4)
这就是SAIR成像的基本原理,其中TM(ξ,η)为修正亮温,包括真实目标亮温和天线辐射图样组成,rij(-τ)为条纹洗涤函数,ξ=sinθcosφ及η=sinθsinφ为方向余弦。为了避免视场混叠和系统偏差,成像前必须进行校正,方法是采用背景对消方法;而对幅度和相位误差,理论上可以用相关噪声注入的方法进行完全校正。为降低系统复杂度,可以采用外部点源照射方法(相关噪声注入方法的一种)进行可视度校正,校正过程可以表示为规范化的可视性背景消除方法如下[10-12]:
(5)
式(5)中:VNORM为校正后的可视度,VT,B,C(u,v) 分别为目标场景、背景场景和点源场景的可视度。对可视度进行加窗处理再进行FT变换即可得到修正亮温的反演图像[1,3]。因此,可视度不确定度会导致重建误差和图像失真,ADC SNR分析应关注其对可视度不确定度的影响。
1.2 可视度不确定度与SNR测量值
可视度的复数形式可写成以下形式[13]:
(6)
Vr及Vi分别表示可视度的实部与虚部,其不确定可表示为:
(7)
式(7)中:σV表示可视度不确定度;σVr及σVi分别表示可视度不确定度的实部与虚部;B是接收机中频带宽,τS是积分时间;TA及TR分别表示天线阵及接收机噪声温度。综合孔径辐射计分辨率与可视度不确定度的关系如下式[3]:
(8)
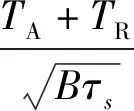
在不考虑天线阵、测量方位角等影响因素时,SAIR成像仪的温度灵敏度与可视度不确定度因子成近似线性关系,该因子是温度灵敏度恶化的直接原因。因此,需要对可视度样本的不同测量值种类和不确定度进行详细分析,制订可视度函数不确定度的误差评价标准。
根据Allan标准差测量方法,可以定义如下参量为可视度测量值的测量SNR,用于可视度不确定度分析:
(9)
SNRVM是可视度测量SNR,σV是包含可视度噪声的不确定度。在常见SAIR辐射计应用中,最差情况的可视度测量值的测量SNR可以估算为:
(10)
式(10)中:Bmin为最小接收机有效带宽,τs,min为最小积分时间。在典型SAIR应用中,如ESTAR、MIRAS及GEOSTAR中[2-4],通常满足Bmin≥10 MHz及τs,min≥0.1 s,因此上述最差SNR计算为30 dB(长基线情况除外)。
由于ADC的噪声会导致等效TR恶化,考虑到天线温度TA和接收机等效噪声温度TR在SAIR信号处理中无法分离,将ADC噪声对可视度测量SNR的影响可以忽略的条件设计为:
(11)
SNRADC(dB)-SNRVM(dB)≥10 dB
(12)
即ADC SNR至少要比可视度测量SNR高10 dB。
对于典型的综合孔径应用系统,如ESTAR、MIRAS及GeoSTAR,其带宽通常在10 MHz,积分时间不会小于0.1 s,因此SNRVM最坏的情况下为30 dB,根据这一点来估算ADC噪声对可视度不确定的影响,即ADC的SNR应大于40 dB。
1.3 窄带零均值高斯噪声的ADC采样SNR与孔径抖动的约束关系
ADC采集时钟的抖动性能需求主要取决于单通道ADC的SNR需求[8]。常用的ADC SNR的RMS合成方法为[14]:
(13)
式(13)中:SNRl,IN、SNRl,Q和SNRl,SJ分别为输入噪声、采样量化噪声和孔径抖动噪声导致SNR下降的线性值。基于辐射计中频信号被认为是窄带高斯噪声并与接收机热噪声相似[15],因此,SNRl,IN独立于ADC的设计,但依赖于所测量的场景。因此应从考虑量化噪声和抖动噪声的ADC理论SNR分析开始ADC的SNR分析。
考虑到SAIR的基带模拟信号常可假设为双边带窄带零均值高斯随机过程信号,ADC最差SNR可采用量化SNR与其他噪声项的叠加方法进行估算,即可以表示为量化SNR与功率峰均比、动态范围和谐波恶化的合成形式[14]:
SNRADC,worst(dB)=SQNRGauss+

(14)
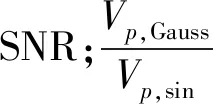
SQNRGauss(dB)=6.02N+4.77-10lg(ηGauss)
(15)
式(15)中,ηGauss为窄带高斯噪声的功率峰均比。根据高斯噪声信号的统计特性,99.999%的峰值电压处于均值左右±4σ的置信区间内,因此噪声幅度的最大值为4σ,高斯信号的峰均比可以表示为[17]:
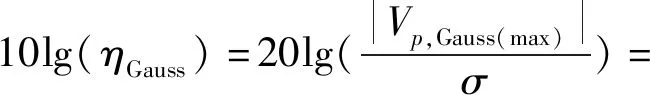
20lg(4)=12.04 dB
(16)
对SAIR基带信号,动态范围常设计为2±1 dB,而谐波失真的影响也非常小,可设置为1 dB。最终实现的ADC SNR通常用有效位数(effective number of bits,ENOB)来表示,即:
(17)
根据上述计算方法,可以得出ADCSNR[18]、理论量化位数、ENOB和ADC时钟抖动RMS值上限之间的约束关系如表1所示(fin=200 MHz)。
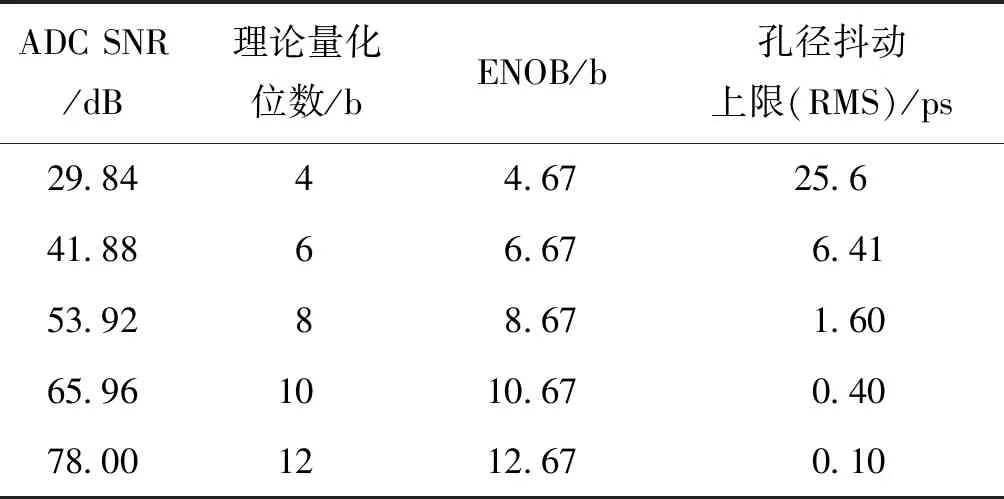
表1 ADC理论SNR与孔径抖动的约束关系Tab.1 ADC SNR requirement specifications(worst cases)
鉴于理论量化位数高于4 b称为高阶量化,而从时钟抖动的可实现性考虑,从6 b理论量化位数开始进行ADC的选型和时钟设计符合上述计算结果。小于1 ps的时钟抖动需要极低的振荡器相位噪声水平,例如需要使用恒温晶振(oven controlled crystal oscillator,OCXO)作为参考振荡器,因此高阶ADC量化的设计重点将集中在理论量化位数为6~8 b的ADC的选型上。
2 高阶ADC对可视度不确定度影响的分析方法
2.1 高阶ADC量化噪声对可视度不确定度的影响分析
ADC噪声和SNR的分析可细化为对输入噪声、量化噪声和孔径抖动噪声分析。SAIR的输入噪声即为对视场内目标和背景进行辐射测量所获得的天线等效噪声温度TA,是有用信号,因此输入噪声无须计入ADC噪声,故将对量化噪声和孔径抖动对可视度不确定度的影响进行详细定量分析。
量化噪声是ADC的一种典型噪声,其产生原因是模拟信号量化过程中最小量化分辨率导致的电压门限判别误差。在高阶采样过程中,量化噪声会导致接收机等效噪声温度升高,且对可视度不确定度的恶化可以在一些假设条件前提下进行定量分析。在仅考虑量化噪声且忽略抖动噪声的前提下,基带模拟信号的量化输出信号可以表示为[19]:
xq[n]=x[n]+e[n]
(18)
式(18)中:xq[n] 代表量化输出信号,x[n]代表理想量化输出信号,e[n]代表由ADC量化引入的噪声。并且满足如下四个假设条件:1)e[n]是平稳的随机序列;2)e[n]与x[n]完全统计不相关;3)e[n]是一个白噪声随机过程;4)e[n]的概率分布在量化误差范围内是均匀分布的。SAIR的基带模拟信号在自然场景辐射下满足高斯分布,在量化位数高于4 b的情况下,认为量化噪声满足上述四个假设条件,并且可以等效为量化噪声温度TQ[9]。为保证ADC量化噪声对辐射测量灵敏度没有恶化影响,设计窄带高斯噪声的量化噪声的最大值为:
(19)
式(19)中:SQNRGauss即为式(16)定义的在窄带高斯噪声的高阶量化SNR。目前典型SAIR系统的ΔTmin=1 K ,而在自然场景下,其他噪声温度可以分别假设为:TA=300 K,TR=500 K,TQ=0.5 K,由此TQ比TA+TR低32.04 dB,满足31.51 dB的可视度测量SNR阈值要求。不同的采样位数下量化噪声TQ占系统噪声TA+TR的比重如图3所示,由仿真结果可知,为满足最高限值为-32.04 dB的可视度测量SNR阈值,量化位数最低值为6.54 b。因此,在ENOB高于6.54 b的ADC采样情况下,量化噪声对可视度不确定度的恶化可以忽略不计。
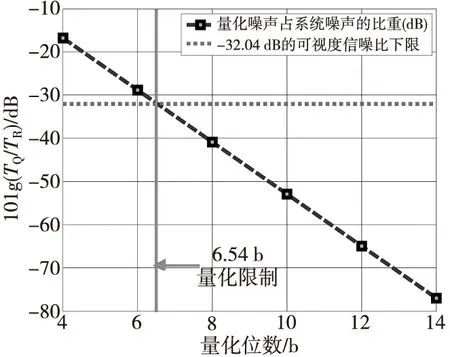
图3 SAIR辐射计量化噪声对系统噪声的贡献Fig.3 Quantization noise contribution in visibility uncertainty
2.2 高阶ADC量化孔径抖动噪声对可视度测量的影响分析
孔径抖动描述的是ADC采集时刻的不确定度,通常满足零均值高斯分布。为保证孔径抖动对可视度不确定度没有影响,设计对其SNR下限如下:
SNRapj,ADC≥SNRADC+6 dB
(20)
如表1所示,ADC的量化位数至少为6 b,最低ADC SNR要求为41.88 dB,则孔径抖动所导致的SNR应高于47.88 dB。
SAIR基带模拟信号的孔径抖动SNR计算方法为[20]:
(21)
式(21)中,σSJ代表孔径抖动的RMS值。设基带截止频率fc=200 MHz,由47.88 dB的SNRapj,ADC下限,可得孔径抖动RMS值的上限为5.56 ps[21-23]。
孔径抖动由时钟抖动、ADC自身孔径抖动和测量仪器抖动噪声本底通过RMS合成组成,但时钟抖动是孔径抖动的主要部分。因此最终馈入ADC器件时钟端口时钟抖动与ADC标称的自身孔径抖动和仪器抖动噪声本底的合成需小于5.56 ps,即:
(22)
即对高阶ADC量化结构,时钟抖动应小于5.56 ps。与其他对系统不稳定性的分析方法类似,时钟抖动也有很多种定量描述方法,其中TIE抖动的RMS值和最大值是通信工业中常用的两种描述方法。TIE抖动的每次跳变测量包含了绝对抖动的全部统计信息,可以直接进行统计计算,求得时钟序列总体抖动情况。在大量采集时钟序列基础上[22],可直接求得TIE抖动的RMS值以评估时钟抖动性能。基于这些优点,选择TIE抖动作为ADC时钟抖动的描述方法。时钟TIE抖动的RMS值表达式为[22-24]:
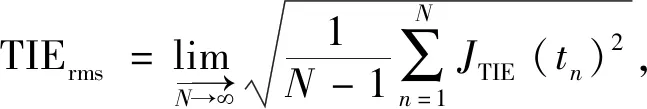
n=1,2,…,N-1
(23)
式(23)中,JTIE(tn)表示第n个时钟边沿的TIE偏差,可为正值或负值。
3 测量结果
以上对采样时钟TIE抖动、时钟抖动SNR及可视度不确定度的分析,已经在一套用于安检的微波实时成像系统BHU-2D-U进行了实测验证,实测结果如下。
3.1 时钟采样抖动
由式(20)—式(22) 分析可知,时钟采样抖动的RMS上限是5.56 ps,时钟网络结构如图4所示,分别在三个测量点对TIE时钟抖动进行测量,其原理框图如图4所示。
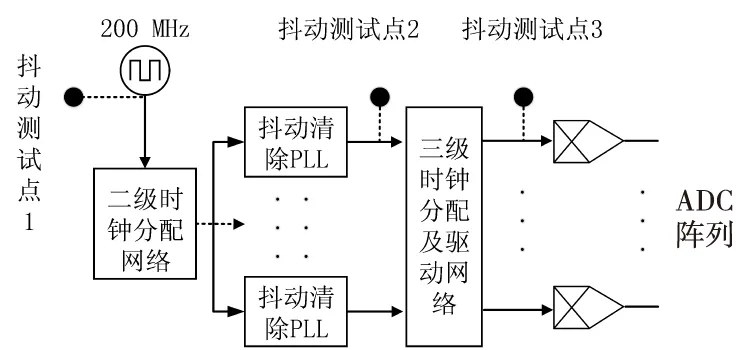
图4 ADC时钟分配和驱动网络原理框图Fig.4 Sampling clock distribution network and time interval error (TIE) jitter measurement positions
由图4可知,参考200 MHz时钟源通过一级时钟驱动、二级和三级时钟分配和驱动网络将时钟信号馈入每个ADC的时钟端口,并在参考源、三级时钟分配网络前后设置了3个抖动测试点。
采用Tektronix DSA72004C高采样率数字示波器和DPOJET软件测量所得TIE抖动如图5所示。在所有抖动测量参数中,唯有TIE抖动利用10 000个采集周期的统计信息计算出了抖动的统计分布,最值和RMS值。图6(a)为FFT频谱示意图,图6(b)为TIE抖动直方统计图,图6(c)为相位噪声测量图,图6(d)为眼图。如图6(a)和图6(b)图所示,200 MHz时钟源实现了2.42 ps的RMS TIE抖动,略高于2.4 ps的积分相位误差等效仿真结果,且满足5.56 ps的约束条件要求;如图6(c)和图6(d)图所示,相位噪声低于-100 dB/Hz,从眼图中可以看出信号质量保障了测量结果。
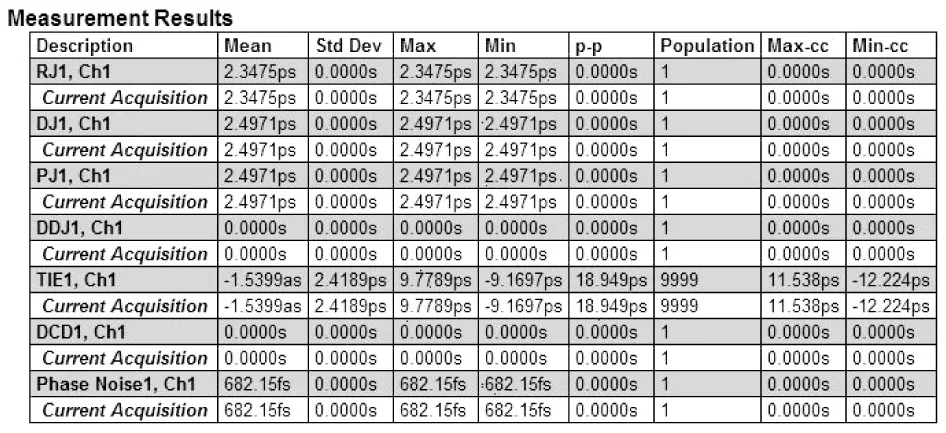
图5 200 MHz时钟源板的TIE抖动测量结果(数值部分)Fig.5 The TIE jitter measurement results of 200 MHz clock source board
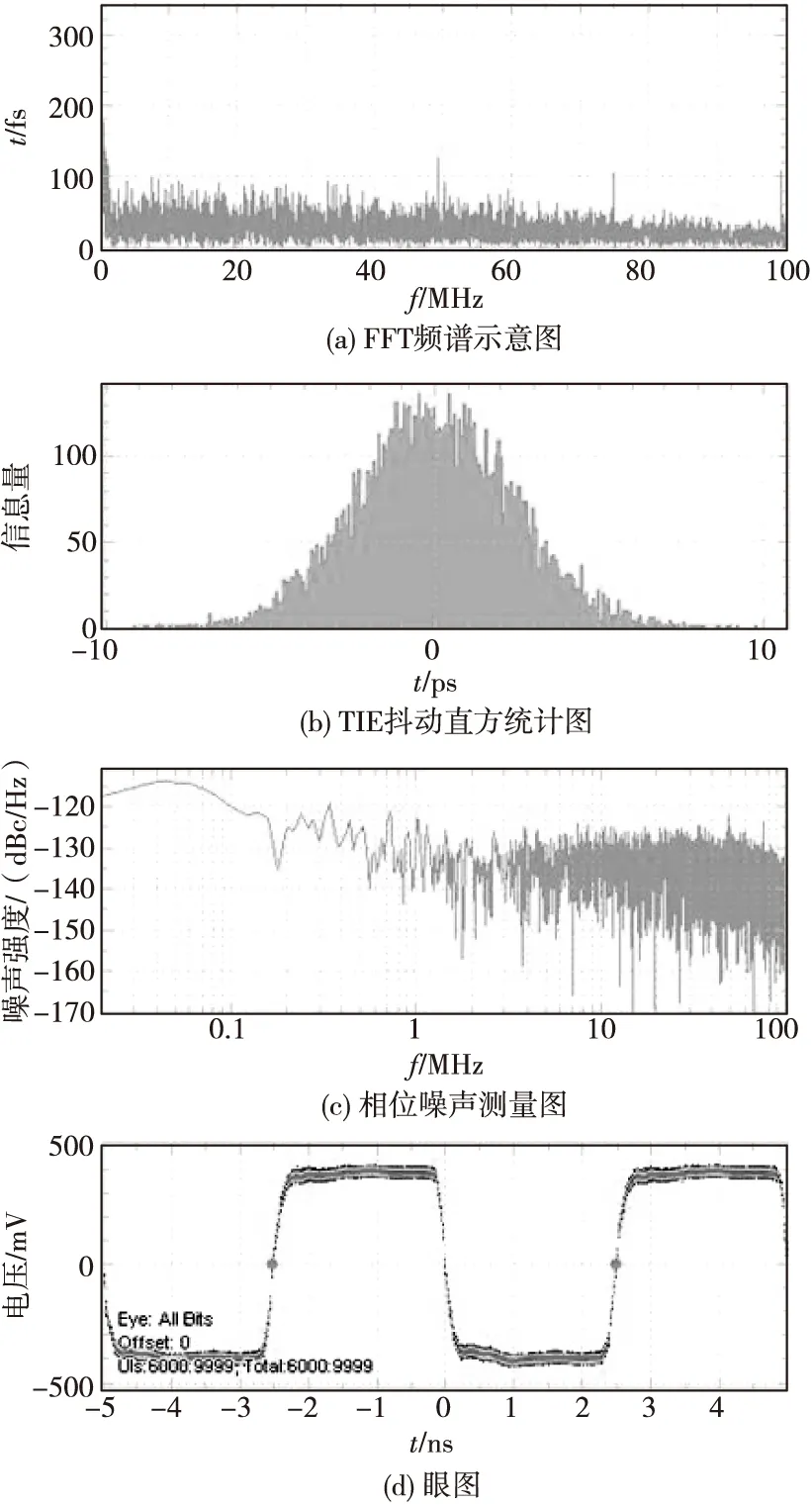
图6 200 MHz时钟源板的TIE抖动测量(图形部分)Fig.6 The TIE jitter measurement results of 200 MHz clock source board
3.2 孔径抖动约束条件
由于两级时钟驱动和分配网络会对抖动产生恶化,因此将时钟源抖动测量8次,抖动清除PLL后的抖动以及最终96路ADC时钟通道的时钟平均分成8组,每组分别测量取最大值,得到各级抖动的实测结果如图7所示。
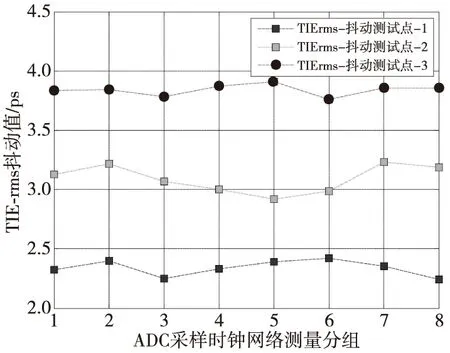
图7 ADC采样时钟网络的TIE rms抖动测量结果Fig.7 The TIE jitter measurement results of ADC sampling clock net
由图7可知,两级时钟驱动和分配网络对TIE抖动的RMS值产生了一定恶化,最终在ADC器件时钟端口处测量到的抖动最大值为3.92 ps。考虑到高阶量化ADC器件AD9480本身存在0.25 ps的自身孔径抖动,而且DSA72004C数字示波器本身存在最大值为0.4 ps的抖动噪声本底,因此96个ADC通道的孔径抖动最差值为:

3.95 ps<5.56 ps
(24)
即总孔径抖动完全满足5.56 ps的约束条件要求。因此,SAIR辐射计基带模拟信号的孔径抖动SNR计算结果为[20]:
(25)
即由ADC孔径抖动导致的SNR为50.86 dB,满足47.88 dB的抖动SNR约束条件。为验证最终ADC的等效量化位数性能,给出实测ENOB的结果如图8所示。

图8 96通道的ADC ENOB测量结果Fig.8 Realized effective number of bits (ENOB) of 96 analog-digital conversion (ADC) modules
在量化噪声和孔径抖动的共同作用下,理论量化位数为8 b的ADC在输入信号频率为190 MHz时实现了6.97 b的ENOB,换算为SNR等于43.72 dB,比表1最低ADC SNR约束条件41.88 dB的理论值高1.84 dB。将ADC SNR与可视度测量SNR作比较可得:
SNRADC=43.72 dB≫SNRVM,max(dB)=
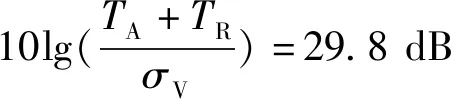
(26)
因此ADC SNR比可视度测量SNR的最大值高13.92 dB,完全满足可视度性能要求。
接收机的条纹洗涤函数和频率响应如图9及图10所示,根据48路中频接收机通道输出结果分析可得,其频率响应的幅度不平衡误差为±0.8 dB群延时,误差±300 ps,对可视度不确定度的影响可以忽略[25]。可视度不确定度的阿拉方差可以用如下公式描述[26]:
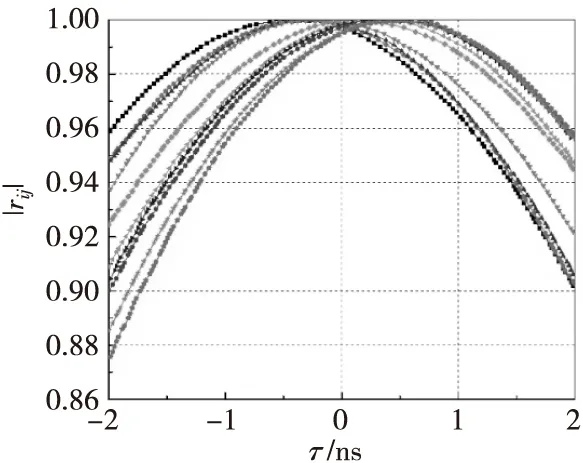
图9 条纹洗涤函数Fig.9 Fringe washing gain loss of 10 visibilities

图10 96接收机通道频率响应Fig.10 Receiver frequency responses of three intermediate frequency receivers (48 I/Q demodulators, DSB 200 MHz)
(27)
(28)
对接收机可视度不确定的阿拉方差测试图及结果分别由图11和图12给出,其平均相关系数为0.12。基于本文提出的ADC SNR的约束方案,在积分时间为0.05~1 s的范围内,可见度不确定度的偏差均在系统限值(1.5%)内,在不降低ADC SNR的情况下同时满足30 dB SNR的限值约束。

图12 接收机可视度不确定的阿拉方差测试结果图Fig.12 Visibility uncertainty deviation measurements by Allan standard deviation
4 结论
通过设计一种用于综合孔径辐射计ADC的SNR的分析方法,研究ADC的SNR对辐射性能的影响。首先提出满足最差情况下的41.88 dB的SNR和6.67 b的ENOB的约束需求;然后证明了针对可视度不确定度,量化噪声与输入无关;为了达到ADC的整体SNR,设定严格的采样抖动约束,采样时钟抖动是采样抖动引起SNR下降的主要原因,通过长统计时间间隔误差抖动的方法对时钟抖动进行评估。由此得出综合孔径干涉辐射计中ADC的SNR约束的分析方法。通过对时钟和采样抖动、总体ADC SNR和可视度不确定度的试验测量,发现实现的ADC SNR SAIR测量SNR提高13.92 dB,比计算SNR提高1.84 dB,验证分析方法的正确性。
基于以上讨论,有如下结论:
1) 接收机的中频信号是自然电磁辐射噪声,取决于被测场景,所以其输入噪声与ADC的SNR无关;
2) 对于量化噪声,证明了通过采用6.54 b以上量化的ADC数模转换的约束条件,综合孔径辐射计中频信号的可视度不确定度的恶化程度能够得到保证;
3) 为了达到综合孔径辐射计的总体SNR,需要严格的采样抖动约束。通过采用高斯随机噪声量化的采样抖动SNR分析这一约束。时钟抖动是导致采样抖动的主要因素,并通过均方根TIE抖动来评估。同时还应注意由分布和传播引起的抖动恶化。
