基于SRUKF-WN的传感器系统偏差估计算法
2020-11-05孙辰辰胡振涛
周 林,孙辰辰,魏 倩,刘 英,胡振涛
(河南大学计算机与信息工程学院,河南 开封 475000)
0 引言
在多传感器多目标融合系统以及多传感器监控系统中,传感器系统偏差配准的目的是准确估计并校正传感器的固有系统偏差,为其后续的融合以及监控过程提供技术保障,其处理好坏将直接影响多传感器信息融合系统融合以及监控的性能与可靠性。
传统的系统偏差配准算法:基于最小二乘配准算法,它忽略了测量误差,把存在的误差完全归于系统误差,且随着数据增大计算量也剧增[1];基于极大似然算法,该算法只解决了二维模型,采用的是地球投影,避免不了配准模型不准确的问题[2]。为了解决配准模型难以确定的问题,H. Karniely[3]提出了用神经网络(NN)算法进行系统偏差配准,但是此方法存在收敛速度慢、易陷入局部最小值问题[4-6]。研究学者不断探索新的有效的网络训练方法,文献[7]提出了基于无迹卡尔曼滤波(UKF)的神经网络算法(UKF-NN),其优点是省去了求解雅克比矩阵的过程,减少了计算量,但是它难以保证系统状态协方差的半正定性从而导致系统无法收敛的问题,不能保证数值的稳定性[8-9]。本文针对上述问题,提出了一种基于平方根无迹卡尔曼滤波(SRUKF)和权值网络(WN)相结合的系统偏差估计算法(SRUKF-WN算法)。
1 权值网络(WN)的系统偏差估计模型
本文构建了包含开始层、中间层以及结束层的权值网络(WN),如图1所示。该WN的主要作用是将网络输入值输入到开始层,将信息层层向后传递,在WN的结束层将网络输出值输出。其中,每一层均由若干个端点组成,层与层之间由网络连接权值进行连接。
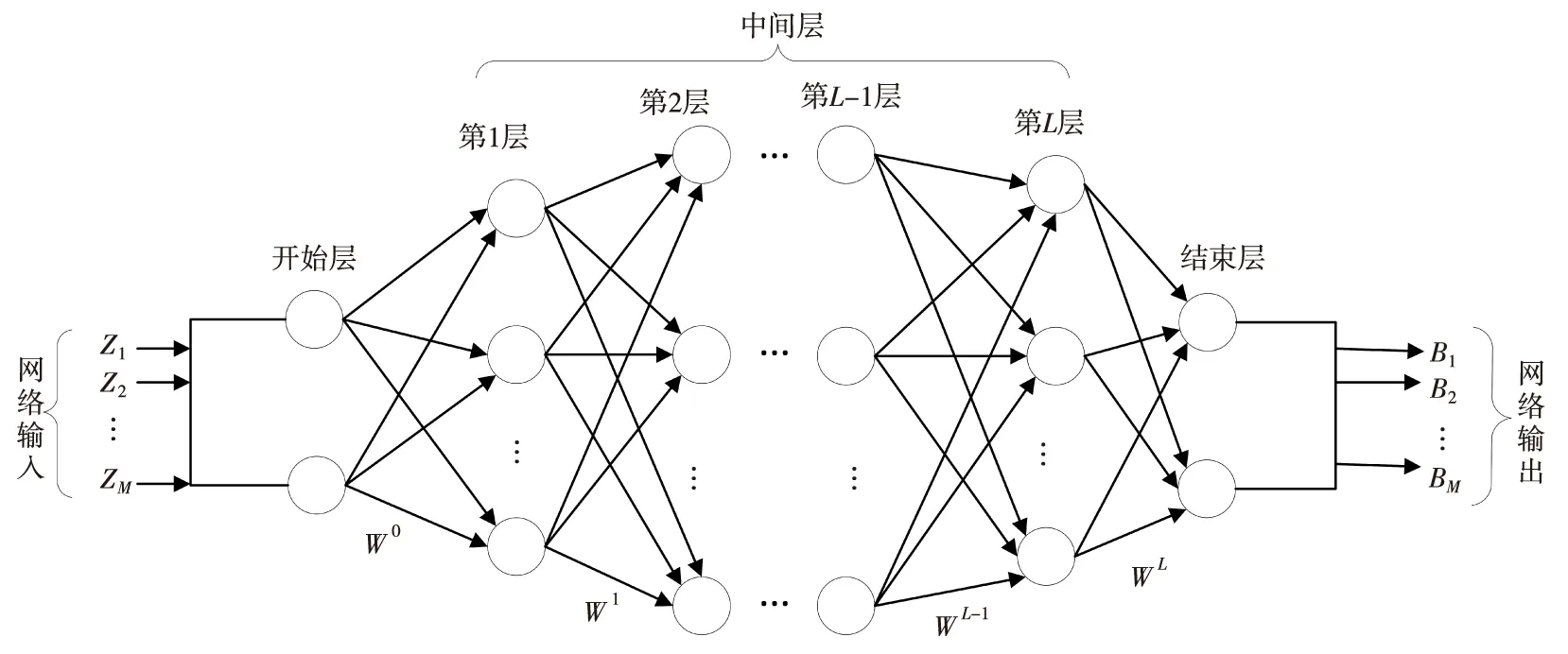
图1 WN模型结构图Fig.1 Structure of WN model
假设有两类传感器A和B,A和B类传感器量测的点迹分别为Z和ZT,其表达式为:
Zi=T+bi+nii=1,…,M
(1)
ZT=T+bT+nT
(2)
式(1)、式(2)中:T代表目标真实的点迹,b和bT代表系统偏差,n和nT代表随机噪声,i代表第i个A类传感器,Zi代表第i个A类传感器的量测值,ZT代表B类传感器的量测值。
A类传感器的精度较低,B类传感器的精度较高(bT和nT的值极小),将B类传感器的量测作为目标的真实状态,A类传感器的量测数据就作为待配准的目标量测。权值网络的系统偏差配准的实质也就是将A的量测映射到B上。当随机误差远远小于系统偏差时(也即ni,nT≪bi,bT),随机误差可以被忽略,也就是要求网络实现Zi=T+bi逼近ZT=T+bT,如果将A类传感器的量测Zi作为网络的输入,则系统偏差Bi也就是Zi-ZT作为网络的输出。用数学公式表达为:
网络的输入值为:
Zi=(xi(k),yi(k))k=1,2,…,N;i=1,2,…,M
(3)
网络的输出值为:
Bi=Zi-ZT=(xi(k),yi(k))-(x(k),y(k))
(4)
WN的模型结构图如图1所示,其数学描述为:
(5)
(6)
(7)
(8)
⋮
(9)
(10)
综上所述,最终的网络输出值可以表示为:
(11)
2 SRUKF-WN算法
UKF对任意非线性问题具有较高的滤波精度,但它对数值计算误差比较敏感,一些舍入误差就会产生负定的状态协方差矩阵,从而导致UKF滤波器不再适用。SRUKF是UKF的平方根滤波形式,在SRUKF算法中,使用状态协方差的平方根矩阵代替状态协方差矩阵参与迭代运算,从而确保状态协方差矩阵的半正定性,保证了滤波的数值稳定性[10-11]。
2.1 状态空间模型及算法框架
若要得到最优的系统偏差估计值,也就是要对权值网络(WN)的网络连接权值进行最优估计,寻找最优的网络连接权值。因此,可将网络连接权值作为状态量,将网络输出作为网络的测量方程。这样就变成了对WN的网络连接权值进行寻优的过程。故SRUKF-WN算法的状态空间模型为[10]:
W(k+1)=W(k)+η(k)
(12)
BZ(k)=B(k)+σ(k)
(13)
B(k)=ST(W(k),Z(k))
(14)
式(12)—式(14)中:W(k)为系统状态向量也即网络连接权值,W=[W1W2WL]T;BZ(k)和B(k)分别为对应于网络输入Z(k)的期望输出系统偏差值与实际输出系统偏差值;ST(·)为WN各层的转移函数的非线性组合;η(k)和σ(k)分别为网络系统的过程噪声和量测噪声,其均值为0,方差分别为Rη(k)和Rσ(k)。
给定初始的W(0|0)和S(0|0),SRUKF-WN算法流程框图如图2所示。Z代表的是目标的量测值,B代表的是传感器的系统偏差值,W代表的是WN的网络连接权值也即状态量,S为状态协方差的平方根矩阵。该算法是将传感器对目标的量测值输入到WN,来计算系统偏差值并将其输出,其中WN的网络连接权值优化过程是通过SRUKF估计系统来实现的。
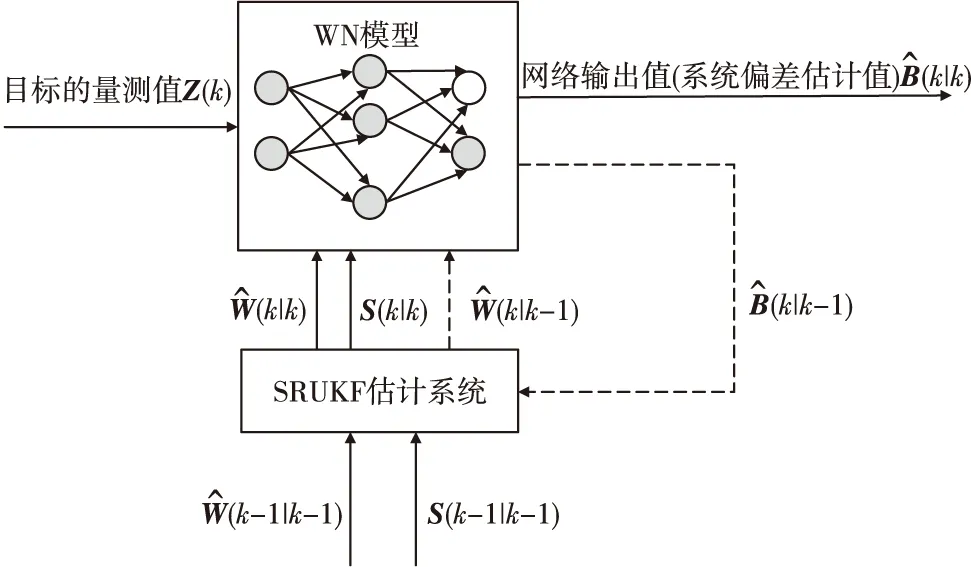
图2 SRUKF-WN系统偏差估计算法框图Fig.2 Block diagram of SRUKF-WN algorithm on systematic biases estimation
2.2 算法实现
本节主要描述的是如何采用SRUKF算法来估计WN的网络连接权值,SRUKF-WN算法主要分为以下几个主要步骤:WN网络连接权值及其协方差矩阵的初始化,网络连接权值sigma点的构建,时间更新,滤波增益的计算以及量测更新,系统偏差估计值的计算。算法的重要描述如下所示:
1) 初始化
(15)
式(15)中,定义矩阵S为方差P的平方根矩阵,通过cholesky分解获得,即P=SST,S是下三角矩阵。
2) 计算W的(2n+1)个sigma点
(16)
3) 时间更新
更新的sigma点:
Wj(k|k-1)=Wj(k-1|k-1)
(17)
对sigma点进行加权融合:
(18)
更新的状态协方差平方根:
(19)
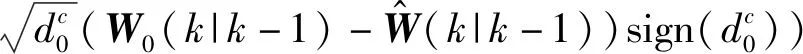
(20)
4) 量测更新
由式(14)得每个sigma点的量测预测值:
(21)
对量测预测值进行加权融合:
(22)
(23)
更新的量测协方差平方根:
(24)
(25)
状态与量测的协方差:
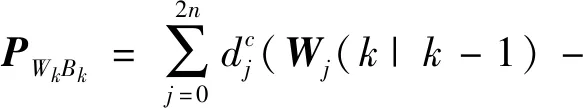
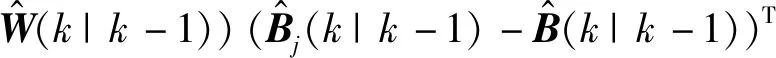
(26)
估计增益为:
K(k)=PWkBk(SB(k|k-1)SBT(k|k-1))-1
(27)
更新的状态变量为:
(28)
更新的状态协方差平方根:
U(k)=K(k)SB(k|k-1)
(29)
S(k|k)=cholupdate(S(k|k-1),U(k),-1)
(30)
5) 系统偏差估计值的计算
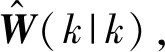
(31)

运用SRUKF算法对WN的网络连接权值进行估计,得到系统偏差估计值。其算法流程图如图3所示,图中的K为最大仿真步长。
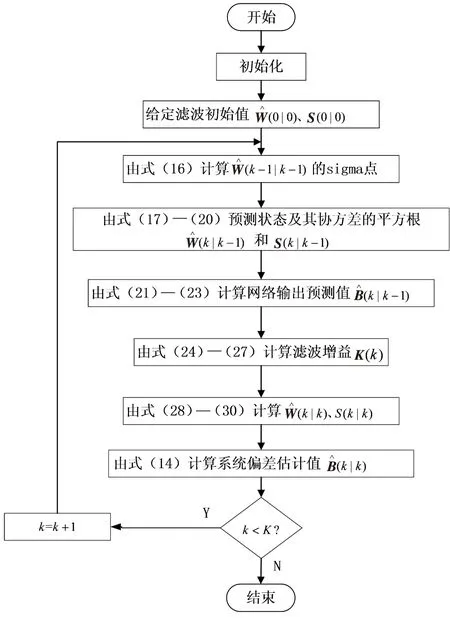
图3 SRUKF-WN算法流程图Fig.3 Flow chart of SRUKF-WN algorithm
3 仿真实验结果及分析
为了说明上述所提SRUKF-WN算法在目标不同运动轨迹上的可行性以及有效性,分别选取了作非机动运动和机动运动的目标进行了如下仿真实验。
3.1 参数设置
1) WN部分
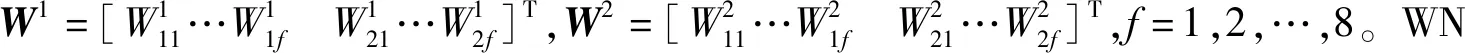
2) SRUKF部分
由于目标的真实运动轨迹难以获得,故分别用两个不同的传感器1和2来观测该目标,传感器1的量测值作为待配准的目标量测,传感器2的量测作为目标的参考真实轨迹。X方向系统偏差设定为-6 m,Y方向系统偏差设定为8 m。由WN的结构可知状态量W的维数n=2×8+8×2=32,α=0.1,β=2,r=0。因为SRUKF是一个不断更新迭代的过程,随着时间的推移,初始值的设置对结果的影响越来越小,所以,这里状态量W的初始值设置为0~1之间的随机数向量。
为了减弱随机噪声以及设置的随机初始值对仿真结果造成的影响,仿真实验采用蒙特卡洛仿真形式,仿真次数为50。采用的仿真环境为Intel i5,主频为3.30 GHz,内存为4.00 GB。仿真软件为Matlab R2014a。
3.2 结果及分析
通过上述所设置参数,并以均方根误差(RMSE)作为算法精度衡量指标,用UKF-NN算法和NN算法作为对比算法,得出目标机动运动和非机动运动下的仿真效果图如图4—图13。
目标的运动方程以及量测方程一般如下表示:
Xmea(k+1)=FXmea(k)+μ(k)
(32)
Zmea(k)=HXmea(k)+Bmea+φ(k)
(33)
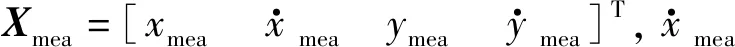
1) 仿真场景一
假设目标在二维平面内作非机动运动。X方向上的速度为3 m/s,Y方向上的速度为4 m/s。Xmea(k)的Xmea初始值设置为[100 m 3 m/s 200 m 4 m/s]T。X和Y方向上的系统偏差值分别设为-6 m和8 m。T为采样间隔,取为2 s。量测矩阵H=[1 0 0 0;0 0 1 0],状态转移矩阵F=[1T0 0;0 1 0 0;0 0 1T;0 0 0 1]。
将作非机动运动的目标的量测值输入到SRUKF-WN算法及其对比算法中,估计出系统偏差值。仿真结果如图4—图8所示。
图4和图5分别为三种算法在X和Y方向的系统偏差估计值(实际输出值)与参考真实系统偏差(期望输出值)的变化。从图中可以看出,SRUKF-WN算法、NN算法以及UKF-NN算法在X和Y方向的系统偏差估计值均趋于参考真实系统偏差-6 m和8 m。NN算法的系统偏差估计值在1~80 s持续下降,80 s之后基本收敛于参考真实系统偏差值。这是由于传统NN算法本质是梯度下降算法,其学习率是固定不变的,必定会造成收敛速度慢的情况。UKF-NN算法由于迭代过程中传递的是状态方差,会出现状态方差负定,从而导致是系统偏差估计值有这样一个过程,即在1~4 s之间下降,4~75 s稳定于真实值,在75 s之后出现剧烈波动。SRUKF-WN算法在迭代过程中传递的是状态方差的平方根矩阵,不会出现状态协方差负定而导致估计值波动的情况。从图中也可以看出,SRUKF-WN算法的系统偏差估计值在0~10 s之间迅速下降,10 s之后收敛于参考真实系统偏差值。
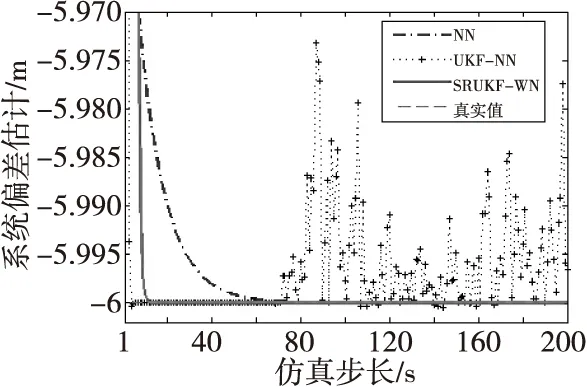
图4 三种算法X方向系统偏差估计值Fig.4 Comparison of the systematic biases estimation in X-axes
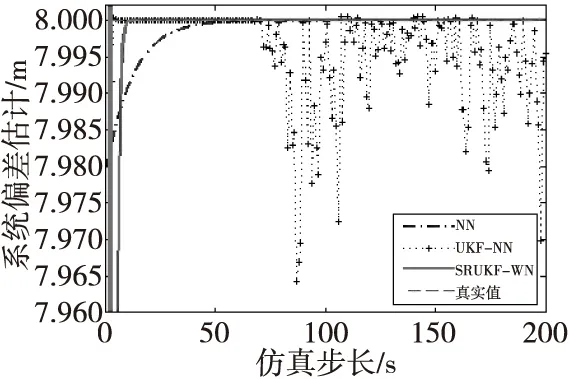
图5 三种算法Y方向系统偏差估计值Fig.5 Comparison of the systematic biases estimation in Y-axes
三种算法在X和Y方向上的系统偏差估计的均方根误差值(RMSE)变化分别如图6以及图7所示。从图6和图7可以看出,SRUKF-WN算法、NN算法、UKF-NN算法的系统偏差的RMSE最终均基本趋于零;但是,UKF-NN算法由于状态协方差负定的原因,在仿真步长大约为75 s之后出现了剧烈波动。
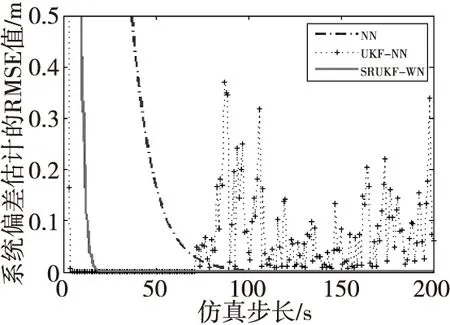
图6 三种算法在X方向上系统偏差估计的RMSEFig.6 RMSE of the systematic biases estimation in X-axes
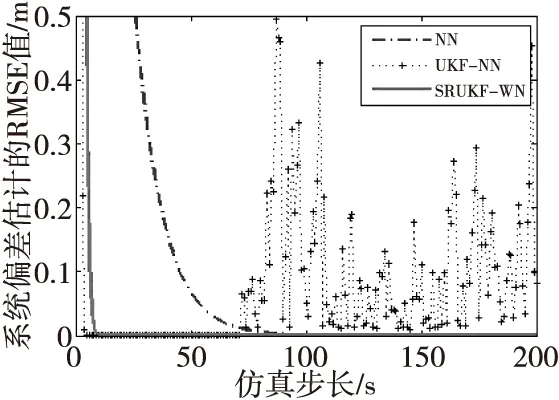
图7 三种算法在Y方向上系统偏差估计的RMSEFig.7 RMSE of the systematic biases estimation in Y-axes
为了能更直观地分析三种算法的性能,在蒙特卡洛仿真次数为50次,仿真步长为200 s的仿真条件下,分别给出三种算法系统偏差估计的平均均方根误差值以及耗时,如表1和表2所示。
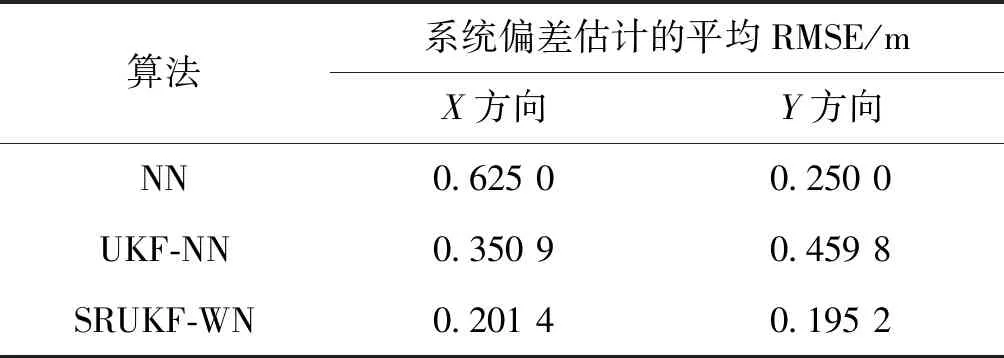
表1 三种算法系统偏差估计的平均RMSETab.1 Average RMSE of systematic biases estimation

表2 三种算法的耗时Tab.2 Running time of three algorithms
由表1可以看出,SRUKF-WN算法在X方向上以及Y方向上系统偏差估计的平均RMSE值分别为0.201 4 m和0.195 2 m,均小于UKF-NN算法和NN算法。很明显地说明了SRUKF-WN算法的精度要高于UKF-NN算法。同时,从表2可以看出SRUKF-WN算法的运行时间为78.9 s,也远远比UKF-NN以及NN算法短。
本文所提SRUKF-WN算法及其对比算法均得出了传感器的系统偏差估计值,然后利用系统偏差估计值对传感器的量测值进行系统偏差配准。非机动运动下三种算法配准前后的轨迹图如图8所示。
从图8可以看出,三种算法在非机动运动下配准后的轨迹均接近于参考真实轨迹,同时说明了所提SRUKF-WN算法的可行性。从图8截取区间214~214.1 m的小图中可以看出,SRUKF-WN算法与UKF-NN算法配准后的轨迹很接近,与NN算法相比更接近于参考真实轨迹;从图8截取区间689.2~689.23 m之间的小图中可以看出,SRUKF-WN算法与NN算法配准后的轨迹很接近,与UKF-NN算法相比更接近于参考真实轨迹。无论仿真开始阶段还是仿真结束阶段,SRUKF-WN算法配准后的轨迹均更接近于目标参考真实轨迹,同时也说明了SRUKF-WN算法的有效性。
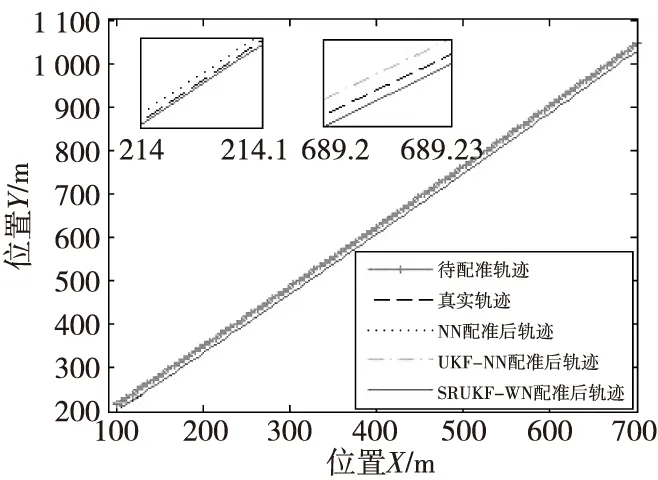
图8 配准前后轨迹Fig.8 Comparison of trajectories before and after registration
2) 仿真场景二
假设目标在二维平面内作机动运动。在上述目标状态方程与量测方程下,机动运动的状态转移矩阵为:
量测矩阵为:
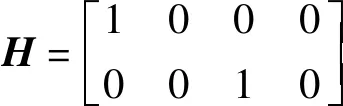
状态转移矩阵中的w表示转弯因子,T为采样间隔。Xmea(k)的初始值Xmea(0)设置为[200 m 8 m/s 100 m 2 m/s]T,X和Y方向上的系统偏差值分别设为-6 m和8 m。在1~100 s,目标右转弯运动,w取值为0.18 rad/s,在101~200 s,目标左转弯运动,w取值为-0.2 rad/s,T取值为0.1 s。
同样地,将作机动运动的目标量测值输入到SRUKF-WN算法及其对比算法中,估计出系统偏差值。仿真结果如图9—图13所示。
图9和图10分别为三种算法在X和Y方向的系统偏差估计值(实际输出值)与参考真实系统偏差(期望输出值)的变化。从图中可以看出,SRUKF-WN算法、NN算法以及UKF-NN算法在X和Y方向的系统偏差估计值均趋于参考真实系统偏差-6 m和8 m。NN算法的系统偏差估计值在1~70 s持续下降,70 s之后基本收敛于真实系统偏差值。这是由于传统NN算法本质是梯度下降算法,其学习率是固定不变的,必定会造成收敛速度慢的情况。UKF-NN算法由于迭代过程中传递的是状态方差,会出现状态方差负定,从而导致系统偏差估计值有这样一个过程,即在1~50 s之间波动,50~160 s稳定于真实值,在160 s之后出现剧烈波动。SRUKF-WN算法在迭代过程中传递的是状态方差的平方根矩阵,不会出现状态协方差负定而导致估计值波动的情况。可以看出,SRUKF-WN算法的系统偏差估计值在0~18 s之间迅速下降,18 s之后收敛于参考真实系统偏差值,没有出现系统偏差估计值波动的情况。
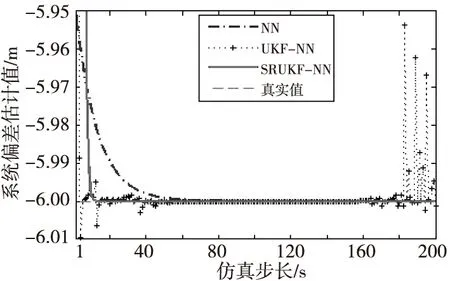
图9 三种算法在X方向上系统偏差估计值Fig.9 Comparison of the systematic biases estimation in X-axes
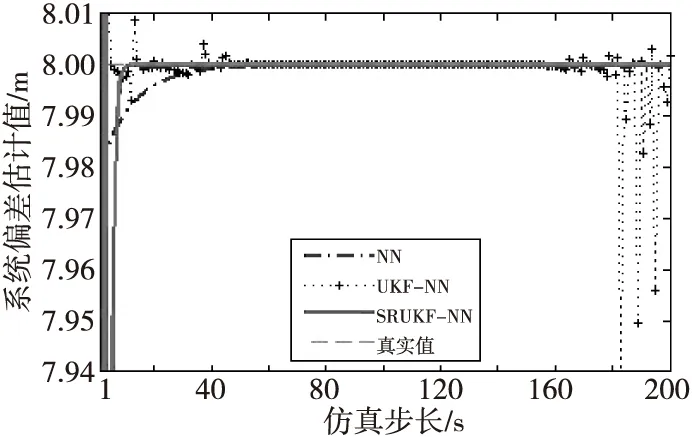
图10 三种算法在Y方向上系统偏差估计值Fig.10 Comparison of the systematic biases estimation in Y-axes
图11和图12分别为三种算法在X和Y方向上的系统偏差估计的均方根误差值(RMSE)变化图。从两幅图中可以看出,SRUKF-WN算法、NN算法、UKF-NN算法的系统偏差估计的RMSE最终均基本趋于零。但是,UKF-NN算法由于状态协方差负定的原因,在仿真步长大约为160 s之后出现了剧烈波动。
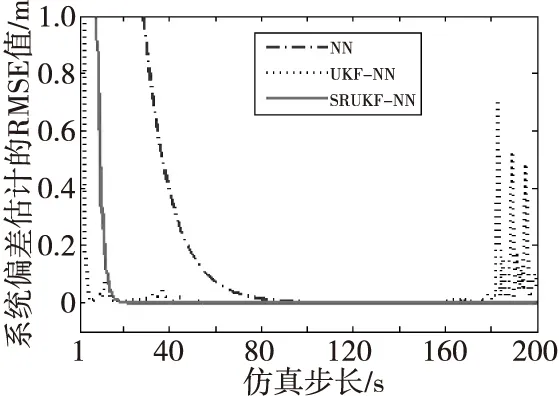
图11 三种算法在X方向上系统偏差估计的RMSEFig.11 RMSE of the systematic biases estimation in X-axes
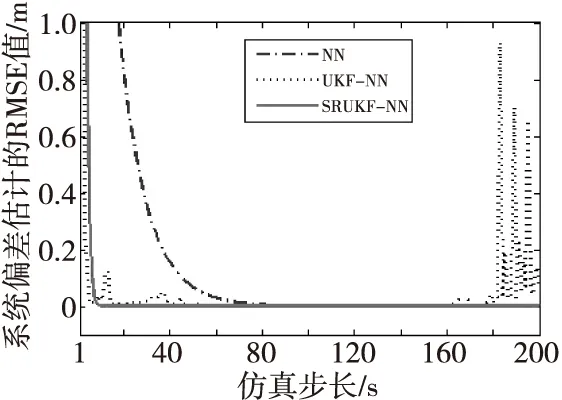
图12 三种算法在Y方向上系统偏差估计的RMSEFig.12 RMSE of the systematic biases estimation in Y-axes
为了更直观地分析这三种算法的性能结果,表3给出了三种算法系统偏差估计的平均RMSE值。
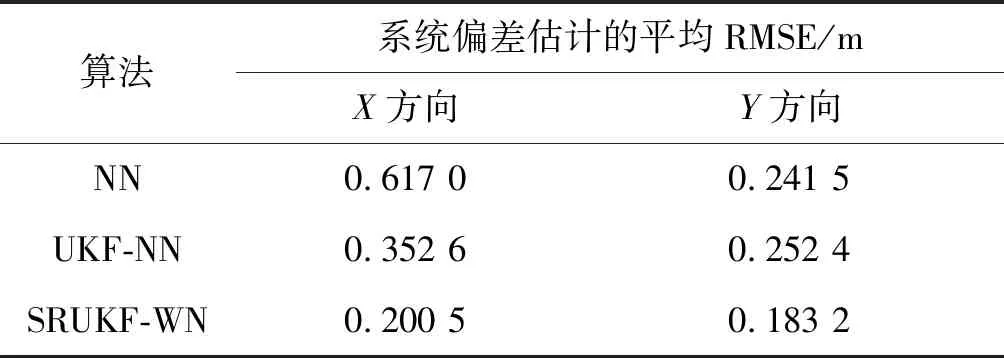
表3 三种算法系统偏差估计的平均RMSETab.3 Average RMSE of systematic biases estimation
由表3可以更直观地看出,SRUKF-WN算法在X、Y方向上系统偏差估计的平均RMSE值分别为0.200 5 m和0.183 2 m,均小于UKF-NN算法和NN算法。很明显地说明了SRUKF-WN算法的精度要高于UKF-NN算法和NN算法。
利用上述所提SRUKF-WN算法估计出的系统偏差值对传感器的量测值进行系统偏差配准。机动运动下三种算法配准前后的轨迹图如图13所示。
从图13中可以看出,三种算法在机动运动下配准后的轨迹均接近于参考真实轨迹,同时说明了所提SRUKF-WN算法的可行性。从区间211~211.4 m以及256~264 m之间的子图中可以看出,SRUKF-WN算法配准后的轨迹更接近于目标参考真实轨迹,即无论是在仿真开始时还是在结束时,SRUKF-WN算法配准后的轨迹均更接近于目标参考真实轨迹,说明了本文所提SRUKF-WN算法的有效性。

图13 配准前后轨迹Fig.13 Comparison of trajectories before and after registration
4 结论
本文提出了基于SRUKF-WN的传感器系统偏差估计算法,解决了系统偏差模型难以构建和难以保证状态协方差半正定性的问题。该SRUKF-WN算法构造了用于计算系统偏差值的WN;建立了包含WN网络连接权值、系统偏差值以及目标量测值在内的系统偏差估计模型,将网络连接权值作为状态量,系统偏差作为量测,构建SRUKF-WN算法的状态空间模型,通过SRUKF算法估计WN网络连接权值;将网络连接权值估计值输入到WN,从而估计系统偏差,并用其来配准传感器对目标的量测值,为后续的目标跟踪提供可靠的量测数据。仿真结果表明,该算法不仅大大减少了算法耗时,收敛速度更快,而且保证了状态协方差的半正定性使得算法精度更高。
