考虑预测不确定性的微网优化调度
2020-11-04郭宁张怡王万申雅茹张亚鹏
郭宁,张怡,王万,申雅茹,张亚鹏
(1.国网宁夏电力有限公司经济技术研究院,宁夏 银川 750011;2.宁夏回族自治区电力设计院有限公司,宁夏 银川 750011;3.国网宁夏电力有限公司固原供电公司,宁夏 固原 756000)
伴随着国际化能源短缺问题和环境污染问题对人类造成的麻烦、对赖以生存的家园造成破坏以及迫在眉睫需要保障电网供电可靠性,发展以分布式电源(distributed generation,DG)组成的微电网(micro-grid)系统受到了越来越多的青睐[1-3]。根据需要,可以选择将微电网与配电网并网运行或孤岛运行。
目前,对于微电网的优化问题主要集中在优化配置和经济调度上。文献[4]提出在微网传统经济调度模型中引入多状态建模,在微网可靠性达标的前提下达到最优配置。文献[5-6]将概率约束与微网孤网模型相结合,着重研究储能装置的寿命损耗对微网经济调度的影响。文献[7]将多目标优化问题转化为单目标优化问题,结合几种不同的微网优化调度策略,研究含电动汽车的微网经济调度问题。文献[8]研究仅考虑微网向大电网购电的条件下,不同调度策略对微网经济运行的影响。文献[9]统一模糊优化与改进遗传算法,研究微网在热电联产条件下的有功优化及无功优化问题,并实现多目标经济调度。文献[10]主要研究如风力发电、太阳能发电等发电方式的波动性对微网经济调度的影响。
本文在传统微网经济调度模型中引入基于区间数和隶属度函数的不确定性模型,用较为简便但又不失可行度的方法构建新模型,最后结合粒子群优化算法得到日前优化调度区间解结果,并对上述结果进行详尽的灵敏度分析。
1 预测不确定性模型描述
本文通过对含有光伏电池(photo-voltaic cells,PV)、风机(wind turbines,WT)、微型燃气轮机(micro gas turbine,MT)、燃料电池(fuel cell,FC)和蓄电池(battery,BT)组成的微网系统分析,选用区间数和隶属函数结合的方法将预测不确定的微网优化问题转换为确定性优化问题求解。
1.1 区间数的引入
区间数(interval number,AI)一般用具有上下界的一组随机变量集合表征不确定性:
(1)

区间数的“中点”和“半径”分别描述某区间数的“好坏”和“偏移”,即:


(3)
引入区间数后,还需要了解区间数的相关运算性质[11],以便求解。
1.2 隶属函数的引入
微网内各个微源和大电网合理配合出力有利于微网经济运行,但为安全性考虑,无法实现微网与大电网的无限制功率交换,引入隶属函数目的在于筛选微网向大电网购电电量区间。

(1)不存在非劣解

(4)
(2)存在非劣解

(5)
μ(x):X→[0,1]
(6)
不同模糊目标的隶属度函数可以根据具体情况选用不同形式,一般确定隶属函数的方法有二元对比法、待定系数法和两点法[12]等。常用的隶属函数有降半矩形分布、降半梯形分布、降半正态分布和降半哥西分布[13]等,也可以根据实际情况中研究对象的不同将其改为升半型隶属函数。
针对判断上述两集合优劣情况,本文又定义下列模糊集:
(7)


1.3 容忍度的引入



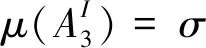

(10)


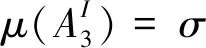
(11)
2 系统运行优化模型
基于上节推导过程及结论,即可确定最终的优化目标,并可以把系统运行优化模型转换为区间数形式。为此,可以将微网中WT、PV有功出力预测和负荷预测分别描述为
特别的,考虑到MT输出功率采用以热定电形式确定,且不考虑热负荷的波动性,则可以把其有功出力表示为

本文采用大电网和微网的交换功率、FC有功出力并配合BT有功输出功率应对预测不确定性。那么,又可以把上述3种有功出力分别描述为
2.1 目标函数及其转换
本文以微网运行成本最低为目标函数进行求解,该运行成本主要包括:微网内各机组燃料费用Cfuel、维护费用CO&M、污染物排放治理费用CD和微网与大电网功率交换成本,具体目标函数为
(12)
式中:Cbuy—购电费用;
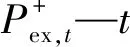
再将该目标函数利用区间数形式和第一节推导结果表示,并稍作修改,转换后的目标函数可以表示为如下形式:
(13)
式中:[Cfuel]、[CO&M]和[CD]—调度日的燃料成本区间数、运维成本区间数和环境成本区间数,且上述三者均可以用微网内各微源发电有功功率区间数形式与各个单位成本的乘积来表示。
需要特殊说明的是,由于FC发电费用较为特殊,即其单位燃料成本与其输出功率不呈线性关系,因此在实际计算过程中选择发电功率区间数中点处的单位燃料成本带入计算。其次,考虑到之前分析过的大电网与微网功率交换的特殊性,且不考虑售电,故在本目标函数中,购电研究对象转换为其中点和半径。
2.2 约束条件及其转换
2.2.1 功率平衡约束
系统在运行过程中,必须满足功率平衡条件,即系统的发电功率与负荷所需功率在每个时刻必须保持相等:
(14)
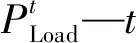
PGU,t—t时刻放弃的电量。
利用区间数关系且不考虑网损,可以把该约束条件表示为
(1)当净负荷为正时

(15)
(2)当净负荷为负时

(16)
2.2.2 微源输出功率约束
系统在运行过程中,必须使其内部微源运行在一定的功率上下限:
(17)
式中:Pi,min和Pi,max—微源i的有功功率输出下限和上限。
2.2.3 蓄电池运行约束
蓄电池的运行状态和荷电状态与蓄电池的使用寿命息息相关,对微网发电系统而言,蓄电池使用寿命越久,蓄电池替换成本就越低,也就越有利于微网的经济调度,故对蓄电池作如下约束:
(18)

2.2.4 有功功率交换约束
大电网不能无限制向微网馈电,需要对大电网与微网有功功率交换设置上下限,故作如下约束:
Pex,min≤Pex,t≤Pex,max
(19)
式中:Pex,min和Pex,max—大电网与微网有功功率交换下限和上限。
考虑预测不确定性的目的在于若功率预测和负荷预测误差较大时,可能会出现微网发电量无法满足负荷的情况,这时,大电网向微网供给的电量呈区间数形式;因此,本文考虑微网与大电网单向功率交换,即微网可以由大电网购电,但无法向大电网送电。利用区间数的关系,又可将上述约束条件表示为
(20)
3 算例分析
3.1 基础数据
本文采用文献[14-15]的微网模型,并闭合公共连接点,研究并网模式下,考虑负荷和可再生能源出力预测不确定性的微网经济优化调度问题。制热收益为0.1元/kW·h;天然气价格取2.5元/m3;微网与大电网有功功率交换上、下限分别取100 kW和0 kW;蓄电池额定容量SBTRC为600 kW·h,且最大、最小剩余容量和初始容量分别为:85%SBTRC、30%SBTRC、75%SBTRC。
各微源相关信息如表1所示,实时电价如图1(a)所示,负荷预测曲线和光伏、风机有功出力预测曲线分别如图1(c)和图1(d)所示,且本文假设上述三者预测精度误差范围均为±20%;热负荷及以热定电后的微型燃气轮机出力如图1(b)所示,且热电比为1.39;各微源污染物排放系数及处理成本见文献[16];本文采用粒子群优化算法[17-19]完成求解过程,且选取算法最大迭代次数为500次,粒子个数取400个,最终计算结果取计算50次之后的平均值。
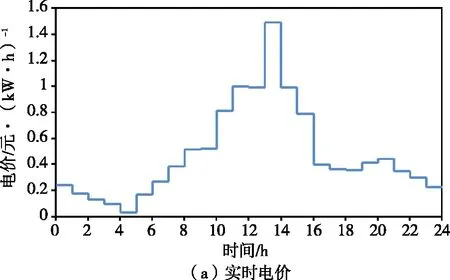



图1 微网已知数据曲线
本文采用日前调度模式,并将该调度周期分为24 h。优先利用WT、PV和MT发出的电量供给负荷,其余电量给蓄电池充电,若仍有余电,考虑到能量单向流动,该部分电量采取弃电措施;若WT、PV和MT发出的电量仍热无法满足负荷所需,缺额部分则由其余微源配合大电网并听从调度指令合理安排出力,在满足负荷需求的前提下,达到经济最优。
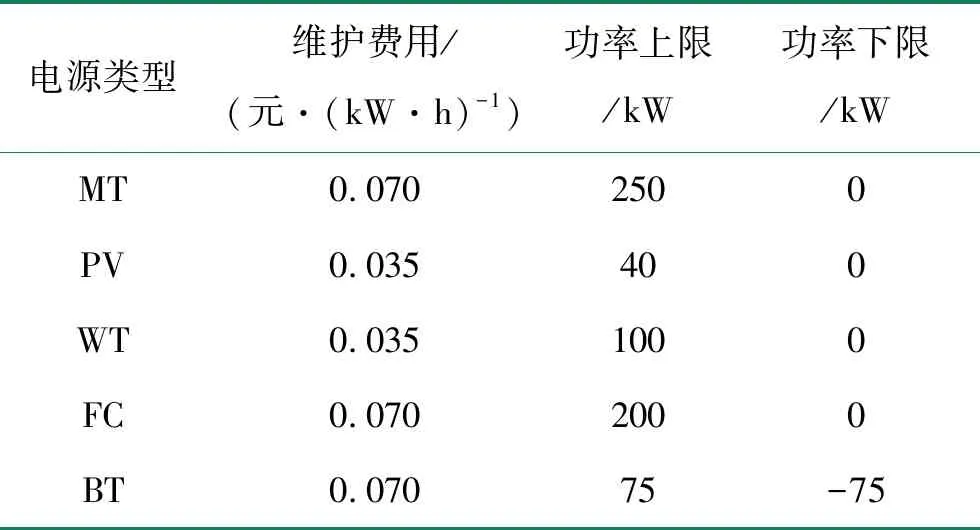
表1 微网各分布式电源机组特性
3.2 结果分析
3.2.1 优化调度结果分析
当容忍度σ取0.3时大电网及微网内各个微源有功出力优化结果如图2、图3和图4所示,首先就微网在不同时间段的不同运行动作进行分析。

图2 容忍度取0.3时FC优化调度结果
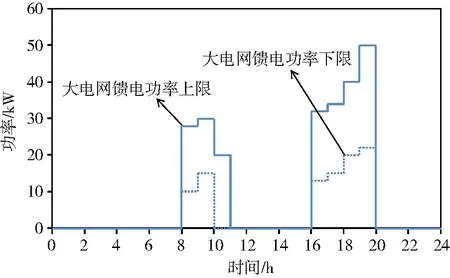
图3 容忍度取0.3时大电网馈电功率优化调度结果

图4 容忍度取0.3时BT优化调度结果
1-6时段(表示01∶00—06∶00,其余雷同),由于光照强度及风力处于调度日较低水平,因此PV、WT出力较少,但此时段微网内部负荷也较轻,微网内部负荷仅存在少量缺额,这部分缺额电量由BT供给即可,FC在该时段有功出力趋近于零。
7-11时段,光照强度及风力呈上升趋势,微网内部负荷需求逐渐上升,PV、WT和以热定电情况下的MT出力已无法满足微网内部负荷缺额,该时段经历了调度日中的第一次负荷高峰期,FC出力逐渐上升并达到上限,BT处于持续放电状态,FC、BT及大电网协同出力满足负荷需求。
12-15时段,风力及光照强度均保持在较高水准,微网内部负荷有所衰减,但也处于较高状态。该时间段,实时电价达到了调度日峰值,除WT、PV和MT供给负荷之外,微网负荷其余缺额主要由FC供给。下时段将经历调度日中的第2次负荷高峰期,因此其余电量充至蓄电池并达到蓄电池电量上限,为下时段做准备。
15-20时段,WT出力和PV出力均有所下降,但微网内部负荷却持续上升,并达到当天最高阶段。在该时间段,WT、PV和MT出力无法满足微网负荷所需,FC出力持续上升,并达到几乎满发状态,BT以较高功率持续放电,且大电网供给电量增多,三者协同调度。
21-24时段,光照强度趋近于0,PV不工作,WT出力也相对较低,微网有功缺额逐渐下降,负荷需求不高。在该时间段,WT、PV和MT出力虽无法完全满足微网负荷,但缺额很少,FC出力逐渐下降,FC除单独供给负荷之外,其余电量均向蓄电池充电,为下个调度日做准备。
当容忍度σ取0.3时,由以上调度结果可以看出:当实时电价处于较高值时,微网较多利用其内部微源供给负荷所需电量,很大程度上减轻大电网供电压力,而在其余时间段,按照经济最优协同调度。在微网负荷较高时,蓄电池出力明显,分担一部分燃料电池在负荷高峰期的供电压力,其余时刻,蓄电池可以根据调度指令选择合适的充放电逻辑,从而使发电系统具有较为灵活的可调度性。在σ取0.3这种运行方式下更加关注的是大电网供给电量的“半径”,即可靠程度,因此在该种运行方式微网发电系统并没有在理论经济最优情况下运行。
3.2.2 灵敏度分析
图5给出了当容忍度σ取不同数值时,微网运行成本优化结果的变化情况(不计调度过程中不变量的成本,包括:MT的燃料成本、治污费用和制热收益,PV、WT和MT的维护费用)。

图5 微网运行成本上下界随容忍度取值变化
由图5可以看出:当容忍度σ取值由0.1到0.9逐渐增大时,微网运行成本下界逐渐减小而微网运行成本上界逐渐增大,且微网运行成本宽度逐渐增大。这说明:当容忍度σ取值逐渐增大时,反之代表其可靠程度的1-σ取值逐渐减少,逐渐增大的微网运行成本宽度表明了在该种变化趋势下,微网决策者需要应对更多的不确定性,从而增加微网调度难度。
因此,在日常微网调度工作中,根据实际需求选择合适的容忍度至关重要,微网发电系统运行成本的减小,是以牺牲其可靠性水平为代价的。以上结论印证了在微网经济调度研究中引入大电网供电满意度目标函数的必要性,同样也说明了未考虑预测不确定性的微网经济调度模型中,在不考虑微网运行成本上下界的情况下,仅仅依靠经济成本确定调度方式的片面性。
图6给出了当容忍度取0.3时,微电网日运行成本随有功负荷预测精度的误差变化。当微网负荷预测无误差或负荷预测波动程度较小时,微网日运行成本相对稳定,成本上下界差距不大;当负荷预测由0到±40%逐渐变化时,发现微网运行成本上界逐渐上升,而微网运行下界呈逐渐下降趋势,即微网日运行成本逐渐变宽,且其变宽程度呈逐渐上升趋势。上述结果表明:负荷预测波动程度越大,微网发电系统不确定性也就越大,微网调度难度也会发生不同程度的增加;因此,在实际微网调度工作中,负荷预测精度越高,调度难度就越低。负荷预测问题的解决,也是保证微网经济调度问题发展的关键因素。
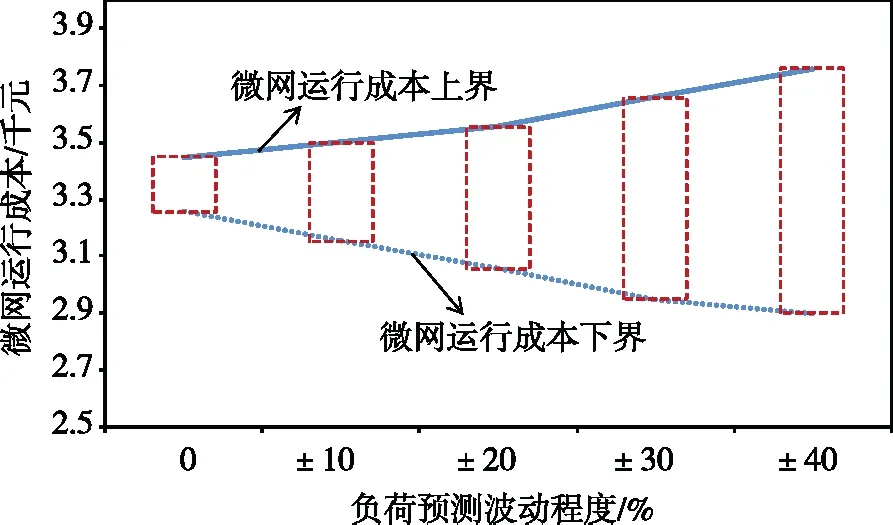
图6 微网运行成本上下界随负荷预测波动变化
4 结 论
本文针对微网运行环境存在的不确定因素,引入基于区间数的容忍度模型,研究微网经济调度问题。通过算例表明,利用容忍度对微网经济性及可靠性的不同决策会对微网调度结果造成影响。研究结果发现:减少微网运行环境的不确定性因素,除提高微网运行可靠性之外,还会降低微网调度难度,从而节约微网运行成本。结论验证了所提模型的科学性和有效性。
