基于开关电磁阀的阻尼可调减振器设计及仿真研究*
2020-11-04刘志强
陶 伟,刘志强,郭 炎
(1.武夷学院 机电工程学院,福建 南平 354300;2.江苏大学 汽车与交通工程学院,江苏 镇江 212013)
0 引 言
减振器是加速车辆振动衰减的主要元件之一,其通过油液在其内部往复运动产生阻尼力,使得振动能量迅速转换为热能,从而达到衰减振动的目的[1-2]。目前,减振器已被广泛应用于包括车架隔振、动力总成隔振等多个隔振领域,为车辆安全运行及乘客的乘坐舒适性提供了可靠保障[3]。
随着半主动悬架研究的迅速开展,阻尼可调减振器也逐渐成为关注焦点[4]。目前,阻尼可调减振器按照设计原理可主要分为两大类,即节流口面积可调式和减振油液粘度可调式[5]。重庆大学的李仕生等人[6]结合能够调节节流孔大小的调节阀,仿真分析了可调阻尼减振器的外特性。江苏大学的江浩斌等人[7]在原被动式减振器结构基础上,设计出了一种基于电磁阀和摆动气缸的可变节流口式可调阻尼减振器,并仿真分析了减振器主要结构参数对其阻尼性能的影响。油液粘度可调式减振器主要包括磁流变液和电流变液两种,其设计核心在于通过磁场或电场迅速改变减振器油液的粘度、塑性等流变特性,从而实现对减振器阻尼状态的有效调节。相较于电流变液减振器,以美国德尔福公司开发的MagenRide为代表的磁流变减振器产品在半主动悬架领域中的应用更为广泛[8]。
从功能角度来看,目前研究提出的节流口面积可调式以及油液粘度可调式减振器均能实现良好的阻尼调节功能,但从应用角度出发,传统节流口面积可调式减振器仍然面临控制精度要求高、设计复杂以及能耗偏大等问题。而油液粘度可调式减振器虽然结构简单、设计要求低,但是对减振油液的可靠性、稳定性要求极高,另外粘度可调油液的使用成本对于一般用户而言,短期内仍难以接受。
针对现有阻尼可调减振器存在的不足,笔者提出一种基于开关电磁阀的新型阻尼可调减振器,即在完成阻尼可调减振器结构设计的基础上,分析其工作原理,而后以阻尼模式3压缩行程为例,建立减振器阻尼特性模型,最后仿真分析减振器主要结构参数对其阻尼特性的影响规律。
1 阻尼可调减振器结构设计
1.1 阻尼可调减振器结构
本文所设计的能够实现多种阻尼状态切换的阻尼可调减振器结构示意图,如图1所示。
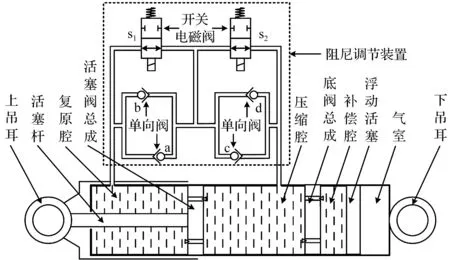
图1 阻尼可调减振器结构示意图
从图1中可以看出,该减振器是在传统液压减振器的基础上,外置一个阻尼调节装置,所述阻尼调节装置是由4个单向阀和2个高速开关电磁阀所组成。
通过相关结构设计,使得减振器油液在复原和压缩行程中除流经活塞阀和底阀之外,还需流经阻尼调节装置。所述阻尼调节装置主要通过控制2个高速开关电磁阀的通断状态,改变减振器油液在阻尼调节装置中的流动路径。由于油液流动路径的不同,形成减振器在相应工作行程中不同的阻尼状态,从而达到调节减振器阻尼特性的目的。
在不同工作行程中,可调阻尼减振器的阻尼状态主要是由4个单向阀的开阀压力所决定,因此,该减振器阻尼调节装置的另一主要特征在于4个单向阀的开阀压力各不相同,具体开阀压力要根据阻尼调节范围要求进行设置。
1.2 阻尼可调减振器工作原理
根据阻尼可调减振器结构示意图可以明显看出,阻尼调节装置通过控制开关电磁阀s1和s2的通断状态,即可改变复原和压缩行程中减振器油液在阻尼调节装置中的油液流动路径。
阻尼可调减振器的油液流动路径如图2所示。
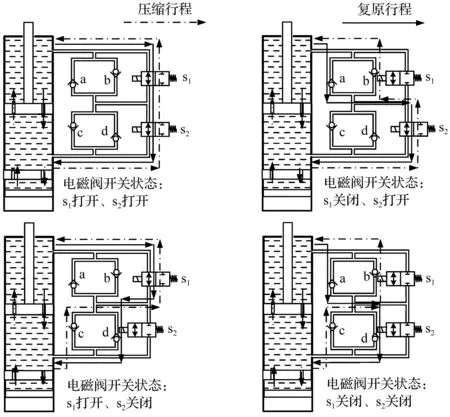
图2 阻尼可调减振器的油液流动路径
从图2中可以看出,不同油液流动路径的显著区别在于油液所必须流经的单向阀不同,从而形成减振器不同的阻尼特性。
结合图1和图2,笔者就压缩行程和复原行程分别阐述阻尼多状态切换减振器的具体工作原理。
1.1 压缩行程
当减振器处于压缩行程时,减振器阻尼特性的主要是通过活塞阀总成和底阀总成中相关流动通道,以及阻尼调节装置中单向阀和开关阀的节流作用来形成,其中,活塞阀和底阀总成中相关流动通道的节流特性不可进行主动调节,因此,减振器阻尼状态的改变主要是由阻尼调节装置中的开关电磁阀通断状态所决定,具体过程为:
(1)当电磁阀s1和s2同时打开时,从压缩腔流出的油液无需经过单向阀直接流向复原腔;
(2)当电磁阀s1关闭、s2打开时,从压缩腔流出的油液首先通过电磁阀s2,但是由于电磁阀s1关闭,油液必须流经单向阀b才能最终抵达复原腔;
(3)当电磁阀s1打开、s2关闭时,从压缩腔流出的油液首先必须通过单向阀c,而后通过电磁阀s1抵达复原腔;
(4)当电磁阀s1和s2同时关闭时,从压缩腔流出的油液必须通过单向阀c和单向阀b才能抵达复原腔。
如前所述,由于4个单向阀的开阀压力各不相同,结合减振器在阻尼调节装置中的4种油液流动路径,即可最终形成4种阻尼状态。
1.2 复原行程
与前述压缩行程类似,减振器阻尼状态的主动调节主要是通过改变阻尼调节装置中开关电磁阀的通断状态来实现,其具体过程为:
(1)当电磁阀s1和s2同时打开时,从复原腔流出的油液无需经过单向阀直接流向压缩腔;
(2)当电磁阀s1关闭、s2打开时,从复原腔流出的油液首先必须通过单向阀a,而后通过电磁阀s2才能抵达复原腔;
(3)当电磁阀s1打开、s2关闭时,从复原腔流出的油液首先通过电磁阀s1,但是由于电磁阀s2关闭,油液必须流经单向阀d才能最终抵达压缩腔;
(4)当电磁阀s1和s2同时关闭时,从复原腔流出的油液必须通过单向阀a和单向阀d才能抵达压缩腔。
在复原行程中,减振器通过阻尼调节装置中4种不同的油液流动路径,也可形成4种不同的阻尼状态。
不同阻尼模式下,电磁阀开关状态和流经单向阀情况如表1所示。
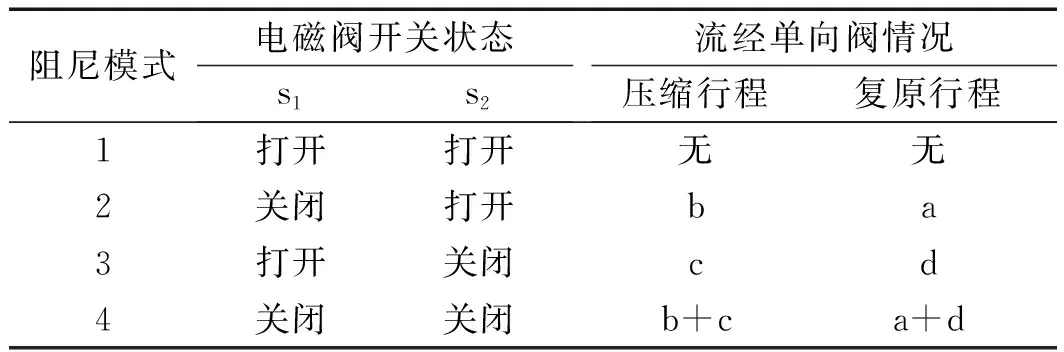
表1 不同阻尼模式下的电磁阀开关状态和流经单向阀情况
2 减振器阻尼特性建模
在减振器阻尼特性建模过程中,值得指出的是,压缩阀和伸张阀的节流阻力均设计为随活塞运动速度而变化。当活塞运动速度较低时,油压不足以克服压缩阀和伸张阀弹簧的预紧力,油液主要通过常通孔隙进行流动;而当活塞运动速度较快时,油压能够克服压缩阀和伸张阀的弹簧预紧力,油液迅速通过压缩阀和伸张阀,从而保证弹性元件的缓冲作用得到充分发挥,同时防止部分零件因超载而损坏[9]。
由于减振器压缩行程和复原行程阻尼特性模型构建类似,本文以阻尼模式3压缩行程为例,建立阻尼可调减振器阻尼特性模型(其他阻尼模式及不同行程下的建模过程与此类似,此处不再赘述)。
根据前文所述,在减振器压缩行程中,压缩阀在不同活塞杆运动速度下的表现状态并不相同,因此,需要针对压缩阀开启前后分别进行建模。
2.1 压缩阀开启前阻尼特性模型
当减振器活塞运动速度较低时,压缩阀未开启,此时减振器压缩阻尼力主要是通过阻尼调节装置中的单向阀c、开关阀s1、活塞总成上的流通阀和底阀总成上的常通孔隙所产生。
因此,压缩阀开启前减振器的油液流动情况,如图3所示。
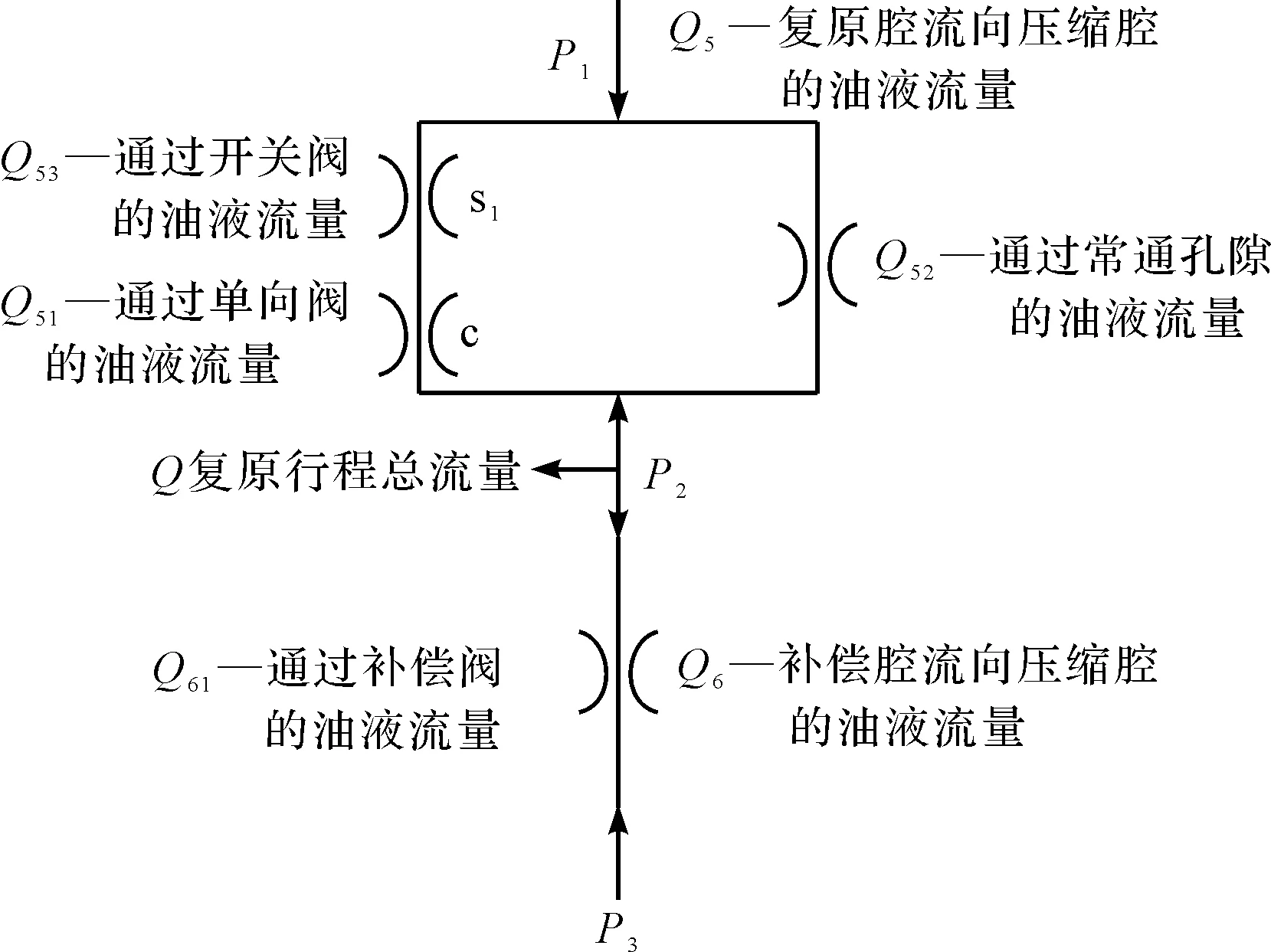
图3 压缩阀开启前减振器的油液流动情况P1,P2,P3—复原腔、压缩腔和补偿腔内的油液压力;P4—气室内的气压
根据筒式减振器的结构原理,压缩阀开启前从压缩腔流向复原腔的油液总流量Q1可表示为:
(1)
式中:Az—活塞横截面积,m2;Ag—活塞杆横截面积,m2;dz—活塞直径,m;dg—活塞杆直径,m;vy1—活塞运动速度,m/s。
由于从压缩腔到复原腔存在2条油路,Q1与通过开关电磁阀s1的油液流量Q13、通过单向阀c的油液流量Q11以及通过流通阀的油液流量Q12之间存在如下关系:
Q1=Q13+Q12=Q11+Q12
(2)
对于单向阀c,通过其的油液流量Q11可表示为[10]:
(3)
式中:Qc—单向阀c的额定流量系数,L/min;ΔPc—单向阀c的额定压力损失,MPa;ΔP21-c—油液流经单向阀c产生的压力损失,MPa。
对于开关电磁阀s1,其可视为一薄壁小孔,因此,减振器在压缩行程中,通过其的油液流量Q13可表示为[11]:
(4)
式中:C—开关电磁阀的压力损失系数;Asv—等效薄壁小孔的截面积,m2;ρ—油液密度,kg/m3;ΔP21-s—油液流经开关电磁阀s1产生的压力损失,MPa。
由于阀片在油液压力下发生变形,从而形成节流缝隙,通过流通阀处的油液流量Q12可表示为[12]:
(5)
式中:δyc—流通阀阀片的变形挠度,m;ΔP21-l—油液流经流通阀产生的压力损失,MPa;μ—减振器油液的运动学粘度,m2/s;ry3—流通阀最大阀片的外径,m;ry4—流通阀最大阀片的内径,m。
流通阀阀片的变形挠度δyc的具体计算公式为[13]:
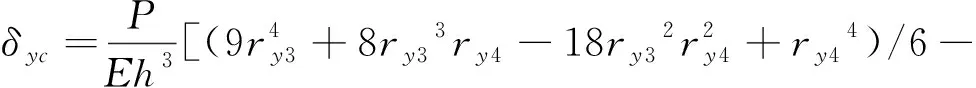
(6)
式中,P—流通阀阀片承受的油液压力,MPa;E—阀片的弹性模量,N/mm;h—阀片厚度,m。
根据图3所示的减振器油液流动情况,压缩腔和复原腔之间的压差ΔP21,与油液流经其他阻尼元件所产生的压力损失间存在如下关系:
ΔP21=ΔP21-c+ΔP21-s=ΔP21-l
(7)
联立上述各式,可最终求得ΔP21的具体表达式,此处不再进行详细推导。
此外,在压缩阀开启前,还有部分油液通过常通孔隙从压缩腔流向补偿腔。设该部分流量为Q2,其表达式为:
(8)
式中:Cd—常通孔隙流量系数,Nk—压缩阀常通孔隙的个数;Ak—常通孔隙的截面积,m2;ΔP23—压缩腔与补偿腔之间的压差,MPa。
根据筒式减振器的结构原理,流量Q2同时与活塞杆进入主筒内的体积有关,因此,Q2的另一表达式为:
(9)
联立式(8,9)可得ΔP23的具体表达式。
根据前文所述,在压缩行程中,由于部分活塞杆进入复原腔内,减振器腔室总体积减小,浮动活塞需要向下移动,从而补偿减小的腔室体积,因此,气室内压力将会增大。
由理想气体状态方程可得:
(10)
式中:P0—气室初始状态内的气压,MPa;V0—气室初始体积,m3;ty—活塞杆向下运动的时间,s。
由于浮动活塞向下移动不会造成压力损失,即P3=P4,则有:
P2=P4+ΔP23
(11)
对减振器活塞进行受力分析,可得压缩阀开启前减振器在压缩行程中产生的阻尼力Fy1的表达式为:
Fy1=AzP2-(Az-Ag)P1
(12)
联立式(11,12),可得:
Fy1=AzP2-AzP1+AgP1=
(Az-Ag)ΔP21+Ag(P4+ΔP23)
(13)
2.2 压缩阀开启后阻尼特性模型
当减振器活塞运动速度较快时,压缩阀开启,此时减振器压缩阻尼力主要是由阻尼调节装置中的单向阀c、开关阀s1、活塞总成上的流通阀、底阀总成上的常通孔隙以及压缩阀所共同产生。
因此,压缩阀开启后减振器的油液流动情况,如图4所示。
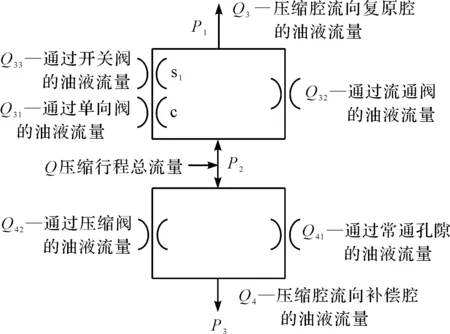
图4 压缩阀开启后减振器的油液流动情况
如图4所示,压缩阀开启后,从压缩腔流向复原腔的油液流量设为Q3,其表达式的推导过程与前文完全相同,即:
Q3=Q33+Q32=Q31+Q32=
(14)
式(14)与前文所述公式的唯一区别在于,流通阀阀片的变形挠度为δyo。因此,根据式(14)同样可以获取压缩腔与复原腔之间的压差ΔP21。
与此同时,压缩阀开启后,从压缩腔流向复原腔的油液流量Q4由两部分组成。其中,参照式(8),通过常通孔隙的油液流量Q41如下式所示:
(15)
参照式(5),可得流经压缩阀的油液流量Q42:
(16)
式中:δys—压缩阀阀片的变形挠度,m。
同理,从压缩腔流向复原腔的油液流量Q4和通过常通孔隙的油液流量Q41,与通过压缩阀的油液流量Q42之间存在如下关系:
(17)
式中:vy2—活塞运动速度,m/s。
根据上式,可进一步计算出压缩阀开启后压缩腔与补偿腔之间的压差ΔP23。
同压缩阀开启前,气室内的气体压力如下式所示:
(18)
因此,压缩阀开启后减振器在压缩行程中产生的阻尼力Fy2可表示为:
Fy2=AzP2-(Az-Ag)P1=
(Az-Ag)ΔP21+Ag(P4+ΔP23)
(19)
3 试验及结果分析
在建立阻尼可调减振器数学模型的基础上,笔者进一步通过仿真试验的方式,来研究阻尼调整装置主要结构参数对其阻尼特性的实际影响规律。
由于所设计的减振器是在传统液压减振器的基础上进行改进,此处仅考虑阻尼调节装置中的结构参数,即仅分析4个单向阀的相关参数以及2个高速开关电磁阀的相关参数对减振器阻尼特性的影响情况,而对于减振器传统结构参数,此处则不作进一步分析。
3.1 单向阀结构参数的影响规律分析
当减振器其他结构参数确定时,不同单向阀a额定压力损失下,减振器阻尼力随活塞运动速度变化情况,如图5所示。
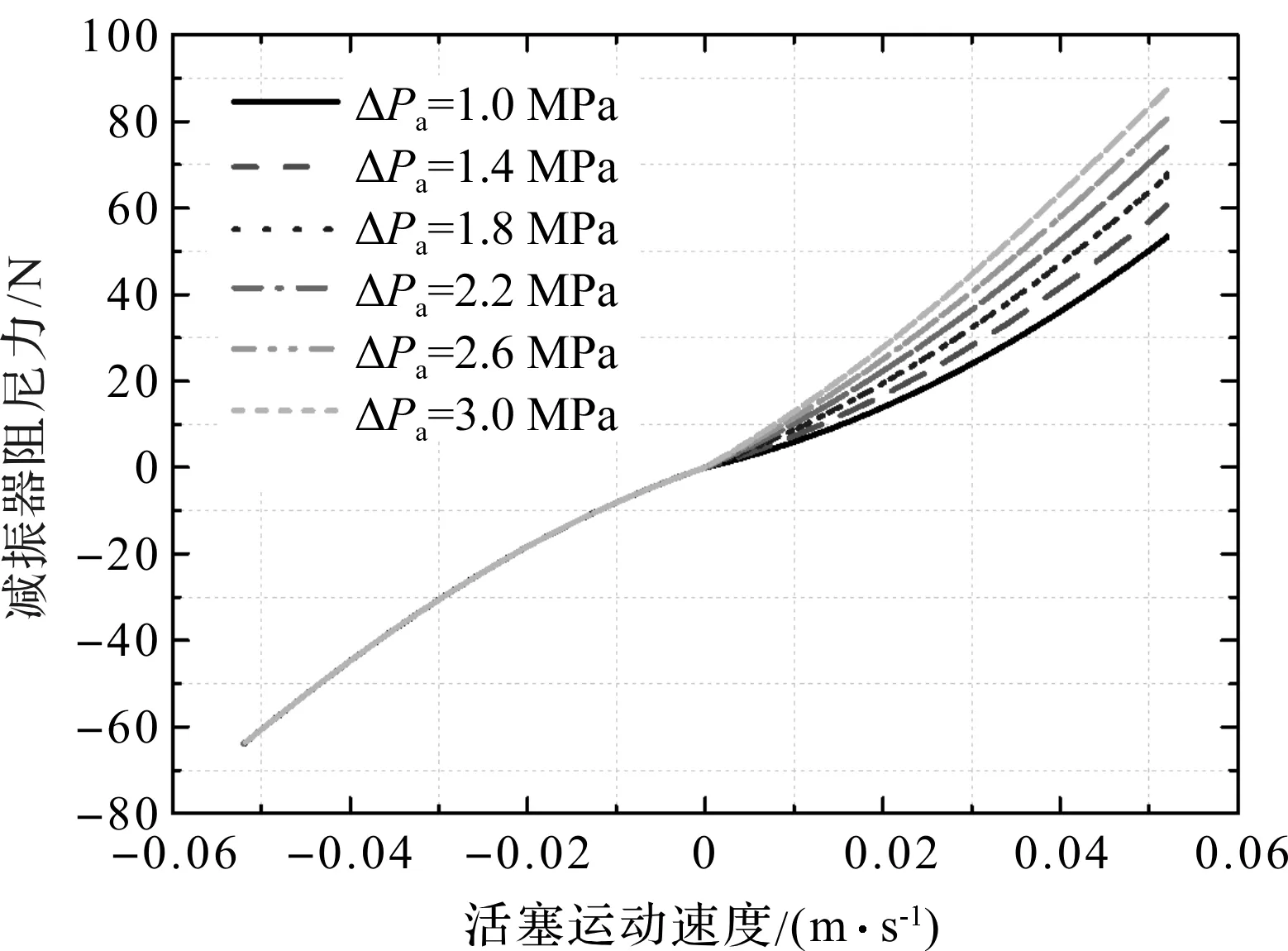
图5 不同单向阀a额定压力损失下的减振器阻尼力随活塞运动速度变化情况
不同单向阀b额定压力损失下,减振器阻尼力随活塞运动速度变化情况,如图6所示。
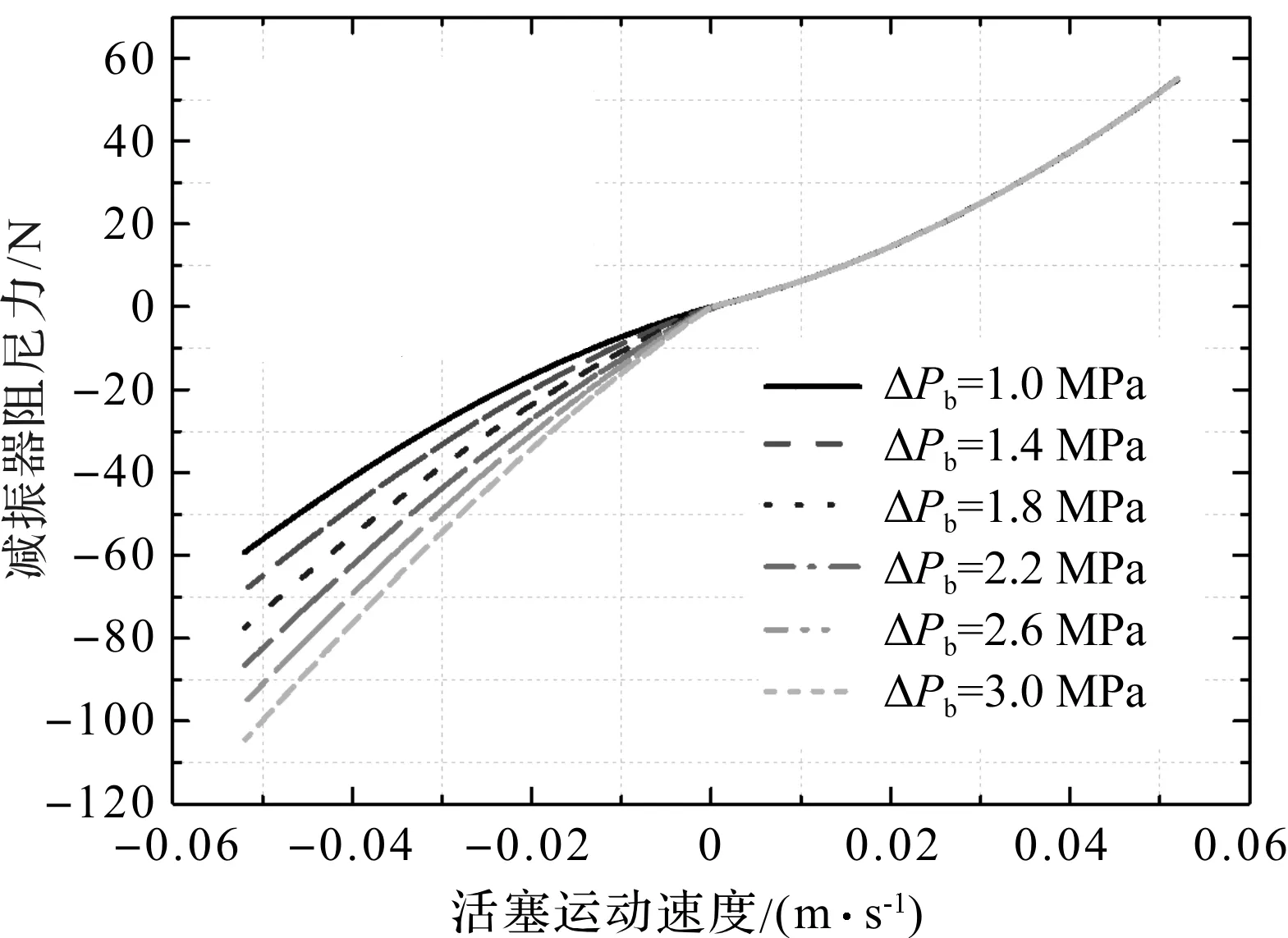
图6 不同单向阀b额定压力损失下的减振器阻尼力随活塞运动速度变化情况
从图(5,6)中可以明显看出:(1)单向阀额定压力损失对减振器阻尼特性存在显著影响,当单向阀额定压力损失增加时,减振器阻尼特性随之明显“变硬”;(2)由于不同阻尼模式下减振器复原行程与压缩行程所流经的单向阀并不相同,单向阀a只影响减振器的复原阻尼力,而单向阀b则只影响减振器压缩阻尼力;该结果与阻尼多状态切换减振器的结构特征相符合。
不同单向阀c额定流量系数下,减振器阻尼力随活塞位移变化情况,如图7所示。
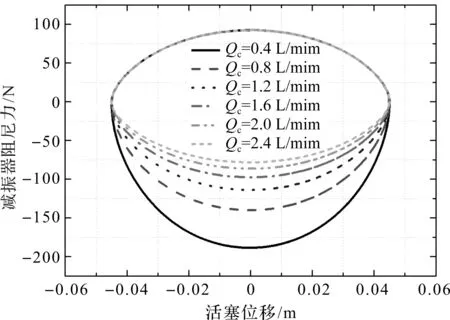
图7 不同单向阀c额定流量系数下的减振器阻尼力随活塞位移变化情况
不同单向阀d额定流量系数下,减振器阻尼力随活塞位移变化情况,如图8所示。
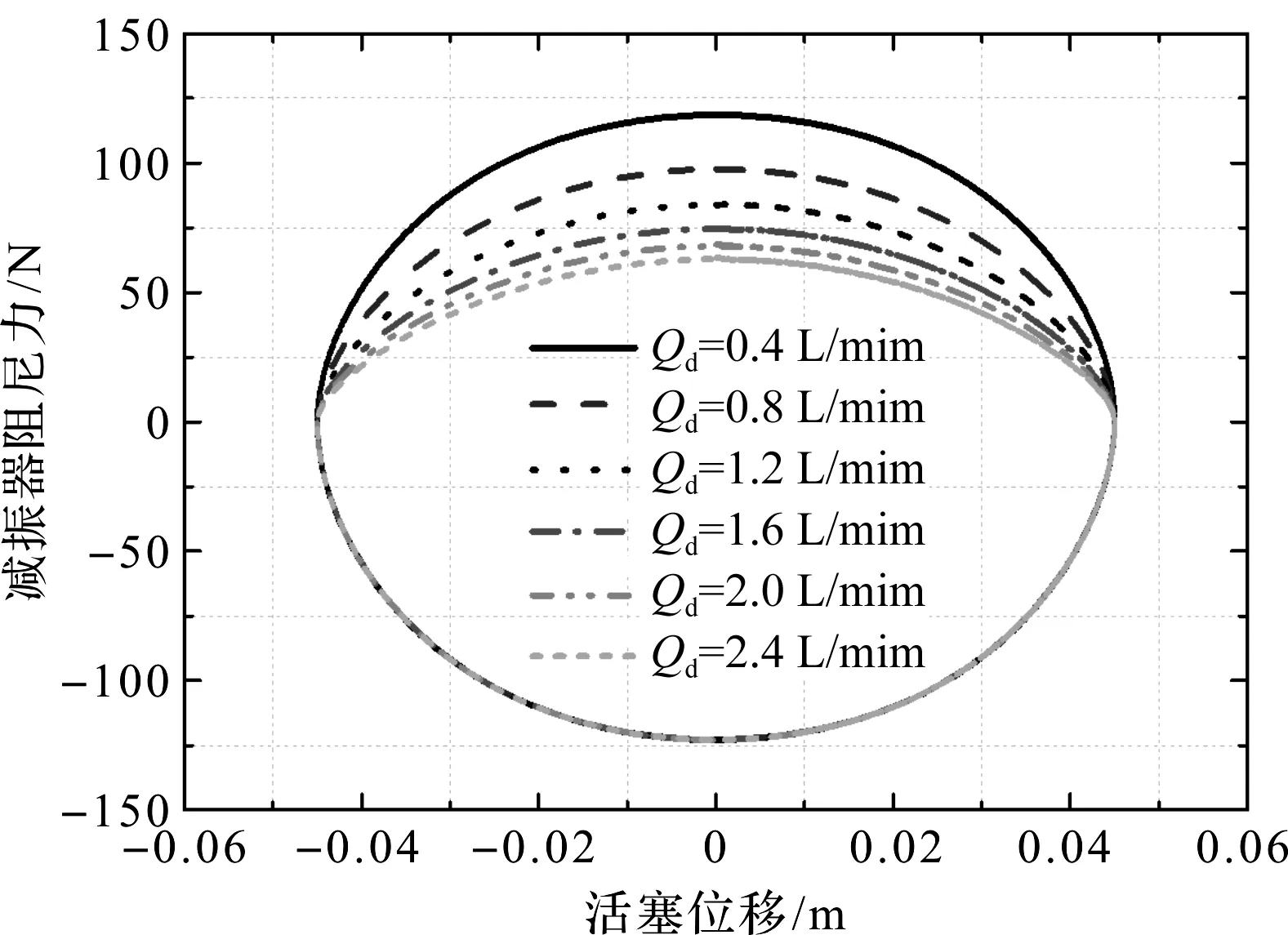
图8 不同单向阀d额定流量系数下的减振器阻尼力随活塞位移变化情况
从图(7,8)中可以看出:(1)单向阀额定流量系数对减振器阻尼特性也存在较为显著的影响,当单向阀额定流量系数减小时,减振器阻尼特性随之“变硬”;(2)与前文分析结论相一致,单向阀d的额定流量系数变化只影响减振器的复原阻尼力,而单向阀c的额定流量系数变化则只影响减振器压缩阻尼力。
3.2 开关电磁阀结构参数的影响规律分析
根据阻尼多状态切换减振器的结构原理可知,阻尼调节装置中除单向阀外,开关电磁阀的结构参数也会对减振器阻尼特性产生一定影响。结合式(4)可知,影响减振器阻尼特性的开关电磁阀结构参数主要是电磁阀等效节流口的面积。
在阻尼模式2中,不同开关电磁阀s1等效节流口面积下,减振器阻尼力随活塞运动速度变化情况,如图9所示。
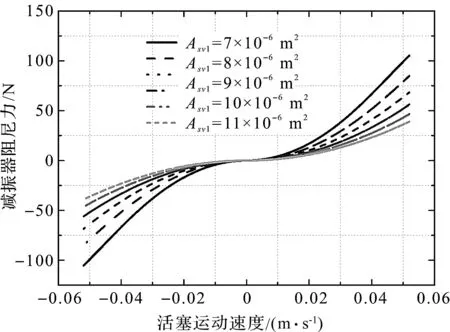
图9 不同开关电磁阀s1节流口面积下的减振器阻尼力随活塞运动速度变化情况
在阻尼模式3中,不同开关电磁阀s2等效节流口面积下,减振器阻尼力随活塞位移变化情况,如图10所示。
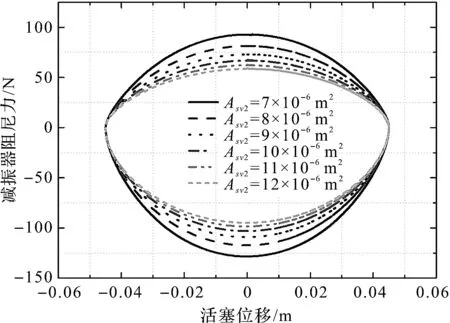
图10 不同开关电磁阀s2节流口面积下的减振器阻尼力随活塞位移变化情况
从图(9,10)中可以看出:(1)阻尼调节装置中的开关电磁阀等效节流口面积对减振器阻尼特性同样具有明显影响;(2)随着开关电磁阀节流面积的减小,不论是复原行程还是压缩行程,减振器阻尼特性均“变硬”,反之则“变软”。
通过上述分析可以发现,为实现减振器的目标阻尼特性调节范围,需要同时协调4个单向阀以及2个高速开关电磁阀的相关结构参数。
4 结束语
针对现有阻尼可调减振器存在的不足,笔者提出了一种基于开关电磁阀的新型阻尼可调减振器。笔者首先设计了基于高速开关电磁阀的阻尼多状态切换减振器具体结构,在此基础上分析了减振器实现阻尼多状态调节的工作机理,在相关建模假设的前提下,以阻尼模式3压缩行程为例,针对压缩阀开启前后,建立了减振器阻尼特性数学模型,结合阻尼模型研究了阻尼调节装置中,4个单向阀和2个开关电磁阀的主要结构参数对减振器阻尼特性的实际影响规律。
研究结果表明,所设计的减振器通过改变两个电磁阀的通断状态即可实现4种阻尼模式、8种阻尼状态,可实现阻尼大范围调节;同时,阻尼调节装置相关结构参数对减振器阻尼特性影响明显,通过调节相关参数即可满足不同阻尼模式对减振器阻尼特性的差异化需求。
该研究结果将为阻尼可调减振器的结构创新设计及主要结构参数的确定奠定一定的基础。
