超越负载下基于李雅普诺夫直接法的电液位置伺服系统研究*
2020-11-04金晓宏张绍峰
阮 军,金晓宏,*,黄 浩,张绍峰
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
0 引 言
在电液位置系统所承受的负载中,有一类负载的方向与执行元件的运动方向相同,此种负载被称为超越负载。超越负载广泛存在于挖掘机动臂下降、绞车释放重物、液压电梯下降等场合[1],其工况下存在质量块的动能转变成执行元件回油腔中油液压力能的过程,若执行元件的回油路无压力,运动部件会因外负载力拖动产生强迫位移,往往会导致系统的输出位移不能准确地跟踪输出指令[2]。
目前,针对超越负载作用下的系统特性与控制策略等研究日趋成熟:李鄂民[3]针对超越负载进行了分析,并总结出了3种液压平衡方法及其各自的适用范围;刘长年[4]提出了利用预开口流量阀或在流量阀负载腔装上连通孔的方法,以使电液伺服系统能够减弱强迫流量的影响;S∅RENSEN K[5]提出了带压力补偿器的平衡阀回路,以减少超越负载波动对系统的影响;范柏利[6]研究了电动机的制动特性,得出了在超越负载工况下可以克服液压系统的速度波动;杨保香[7]在进液油路和回液油路增加了两位三通先导式方向控制阀,以避免液压缸真空的形成;LEE J C[8]提出了通过双阀芯控制技术实现进出口的解耦,采用了两级控制结构,在实现调速控制的同时提升了系统的节能特性;LIU B[9]在采用负载口独立技术保证系统速度控制特性的前提下,提出了压力流量复合控制策略,进一步提高了系统的稳定性能;CHENG M[10]通过反馈两腔压差的变化率调整了阀口开度,采用泵阀联合控制保证了在超越负载工况下的系统可控性;HU Quan-yi[11]提出了集成电液三通减压阀的负载敏感技术可保持阀口压降的恒定;KIM W[12]提出了增益负载观测器与自适应控制相结合的方法,将负载作为未知状态进行观测,以补偿参数不确定性和时变负载对系统的综合影响。
以上对于电液位置系统消除超越负载影响的研究,绝大多数都是在回油路上提高背腔压力,以平衡超越负载[13],而当液压缸活塞已在外负载力作用下被动运动引起强迫位移时,会导致位置系统失去控制。基于Lyapunov直接法的控制器设计则具有设计简便直观、无需对模型进行转换或递推等优势,只要确定了适合于该系统的Lyapunov函数,则可方便地推导出所需的控制律[14]。
本文将超越负载对电液位置系统的影响视为由强迫流量引起的速度扰动来处理,根据系统的误差状态方程提出一种形式简单的Lyapunov函数,通过Lyapunov直接法的反演方式得到求取控制律的一般性方法,并依据Lyapunov直接法所得到的控制率,构造前向通道串联微分控制补偿器和与动力机构并联的带可调液阻机液补偿器,以期减少超越负载对系统跟踪性能的影响。
1 问题描述
电液位置控制系统(以下简称为位置系统)主要由伺服放大器、电液伺服阀、液压缸和位移传感器构成。
位置系统的工作原理示意图如图1所示。
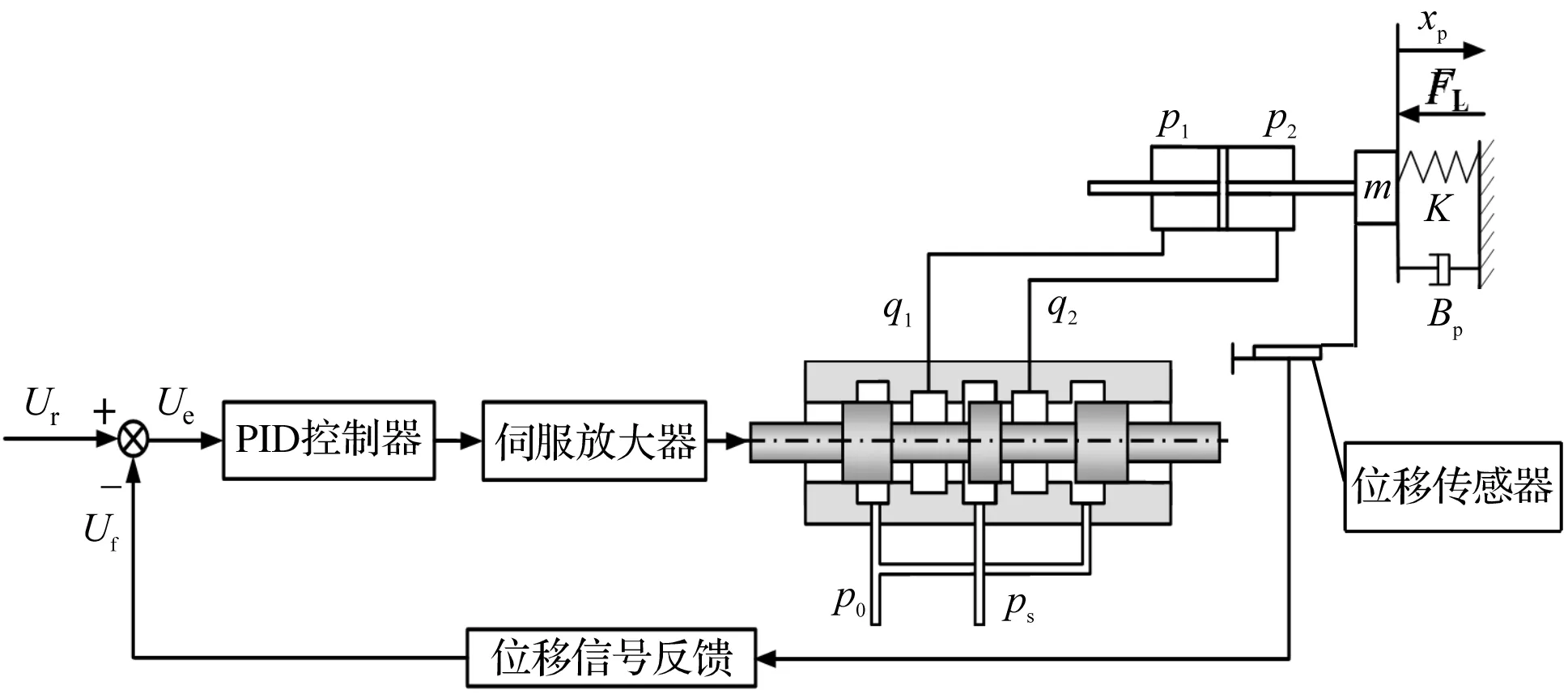
图1 电液位置控制系统原理示意图
图1中,取活塞杆向右移动为正方向,假定液压缸没有外泄漏,左、右两腔初始容积相等且腔内处处压强相等,正常情况下,位置系统利用液压能源通过液压缸中的活塞来驱动负载,因而负载流量的流动方向是从高压油源到油箱,且负载压力的绝对值永远小于或等于能源压力[15]。
图1中,液压缸左腔通高压,右腔与回油路相通,外负载力FL方向与活塞运动方向相反,在负载压力pL的作用下,执行件m向右运动,此时负载压力pL与负载流量qL方向相同。如果作用在执行件上的外负载力FL突然换向,并拖动执行件以更快的速度向右运动,则右腔的压力将升高,而左腔的压力将降低,此时pL=p1-p2<0,出现了负载压力pL与负载流量qL方向相反的现象,即超越负载工况。过大的超越负载作用下,容易出现位移这一被控制量不可控现象,影响位置系统的控制精度[16]。
2 系统数学模型及强迫流量分析
参照文献[17],在外负载力FL作用下,以电液伺服阀阀芯位移xv为输入,液压缸活塞杆的位移xp为输出,可以得到如下拉氏域表达式:
(1)
式中:Kq—阀口流量增益,m3·s-1·m-1;A—液压缸控制腔活塞的有效面积,m2;Xv—伺服阀阀芯位移,m;G1(s)—一阶特征多项式;FL—活塞上的负载力,N;R1,R2,R3,R4—特征变量。
其中:
G1(s)=Kce(1+Vts/4EeKce)/A2
(2)
式中:Kce—总流量-压力系数,m3·s-1Pa-1;Vt—液压缸总有效容积,m3;Ee—油液有效体积弹性模量(包括液体、混入油液中的空气及工作腔体的机械柔度),Pa。
特征变量R1、R2、R3、R4分别为:
R1=mVt/(4EeA2)
(3)
式中:m—活塞及负载折算到活塞上的总质量,kg。
R2=R21+R22=mKce/A2+BpVt/(4EeA2)
(4)
式中:Bp—黏性阻尼系数,N·m-1·s。
R3=R31+R32+R33=1+BpKce/A2+KVt/(4EeA2)
(5)
式中:K—负载弹性刚度,N/m。
R4=KceK/A2
(6)
在超越负载工况下,外负载力FL方向与活塞运动方向相同,活塞在FL拖动下向右运动产生强迫位移,右腔体积缩小,腔内产生了附加的强迫流量,该流量导致右腔压力在原有p2基础上有所增加;左腔体积增大,压力相应的在原有的基础上有所减小,当pL=p1-p2<0时,出现负载压力pL与负载流量qL方向相反的现象,随着液压缸活塞右腔的压力逐渐升高并达到p2>ps时,回油腔流量q2继续增加且强迫流量无法及时排出,出现q2>q1的流量不连续现象,左腔不能被充满,形成一部分空腔,此时会出现活塞杆输出位移对指令信号的跟踪不连续现象。过大的超越负载会导致位置系统失去控制,其表现为动作不按指令运行。
综上可知,超越负载引起的强迫流量是产生位置系统误差的最主要因素,抑制强迫流量就成为提高位置系统跟踪精度的重要任务。
根据式(1)可得出系统控制框图,如图2所示。
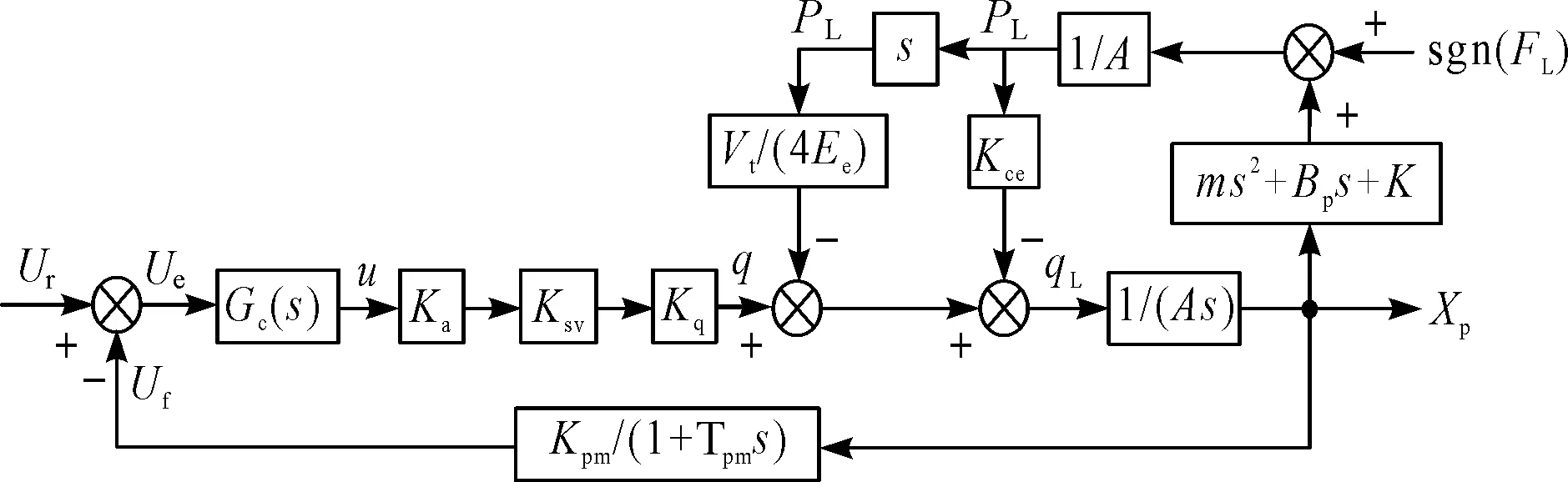
图2 位置系统传递函数框图Gc(s)—系统校正环节传递函数;Kpm—位移传感器增益;Tpm—位移传感器的时间常数;qL—负载流量;PL—负载压力;Ka—伺服阀放大器增益,A/V;Ksv—伺服阀的流量增益,m/A;Kq—阀口流量增益,m3·s-1·m-1
由图2可知,在超越负载情形中,FL方向与xp方向相同,液压缸产生的强迫流量将助长活塞杆的运动,且强迫流量的大小与FL和FL的变化率有关。
式(1)中,分子的第一项表示稳态时阀芯位移所引起的液压缸活塞的输出位移,第二项表示FL作用所引起的活塞输出位移的减少量。其中,分子第二项[Kce(1+Vts/4EeKce)/A2]FL又可分解为FLKce/A2和FLsVt/(4EeA2),FLKce/A2表示FL作用在活塞上的压差引起的活塞速度变化,FLsVt/(4EeA2)表示在FL变化时液压缸两腔油液体积变化引起的活塞速度变化。
在超越负载工况下,FL方向变为与活塞杆运动方向相同,进而产生强迫流量qF,其表达式为:
qF=FLKce/A+FLsVt/(4EeA)
(7)
由式(7)可知,在位置系统中,超越负载引起的强迫流量值与FL的大小和负载压差随时间的变化率成正比,与油液弹性模量成反比。因此,要消除超越负载对系统的影响,需要对超越负载作用下的油液体积变化时,引起的压缩流量和泄漏流量进行补偿。
3 系统问题求解
3.1 系统状态方程
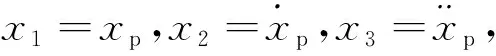
根据式(1)可得系统的状态方程为:
(8)
其中:
a1=R4/R1=4KKceEe/(mVt);
a2=R3/R1=(4EeA2+4BpKceEe)/(mVt)+K/m;
a3=R2/R1=4KceEe/Vt+Bp/m;
dL=FLKce/A2+FLsVt/(4EeA2);
b=4KaKpmKsvKqEeA/(mVt)。
3.2 误差状态方程
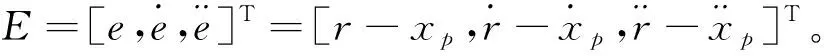
由此可得:
(9)
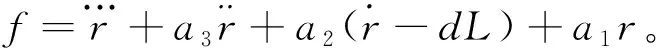
3.3 控制律求取
此处利用Lyapunov直接法的反演方式求解系统稳定的有关项U,并将其嵌入到系统非线性方程中,以抵消或者削弱不稳定因素对系统的影响,即探寻式(9)的Lyapunov函数V(e),并根据V(e)正定,其偏导数负定这一系统稳定条件,求出嵌入项U的表达形式。
取式(9)的Lyapunov函数为:
V(e)=[(e1+e2)2+(e1+Je3)2+(e2+Le3)2]/2
(10)
式中:J,L—非零常数。
其中:
J+L≠0
(11)
观察式(10)可知,该函数在平衡点(0,0,0)外的点均是大于0的,因此其满足正定条件。
对式(10)求导可得:
(12)
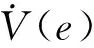
(13)
将其代入式(12)可得:
(14)
式(14)中第一项可能构成完全平方式,此处令其为N,即:
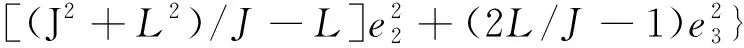
(15)
由此可知,当式(14)中系数满足条件[2(J2+L2)/J+L/J-(J+2)]2=4([(J2+L2)/J-L]×(2L/J-1)时,式N恒小于0。其中:I,H—非负常数。
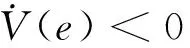

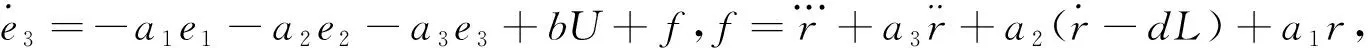
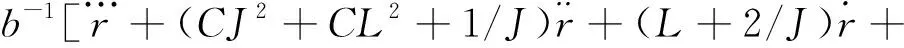
(16)
3.4 稳定性证明
将式(16)代入式(12)可得:
(17)
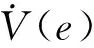
4 位置系统结构补偿方案
将式(16)中的嵌入项加入式(1)所示的系统模型中,可绘制出系统的控制框图,如图3所示。
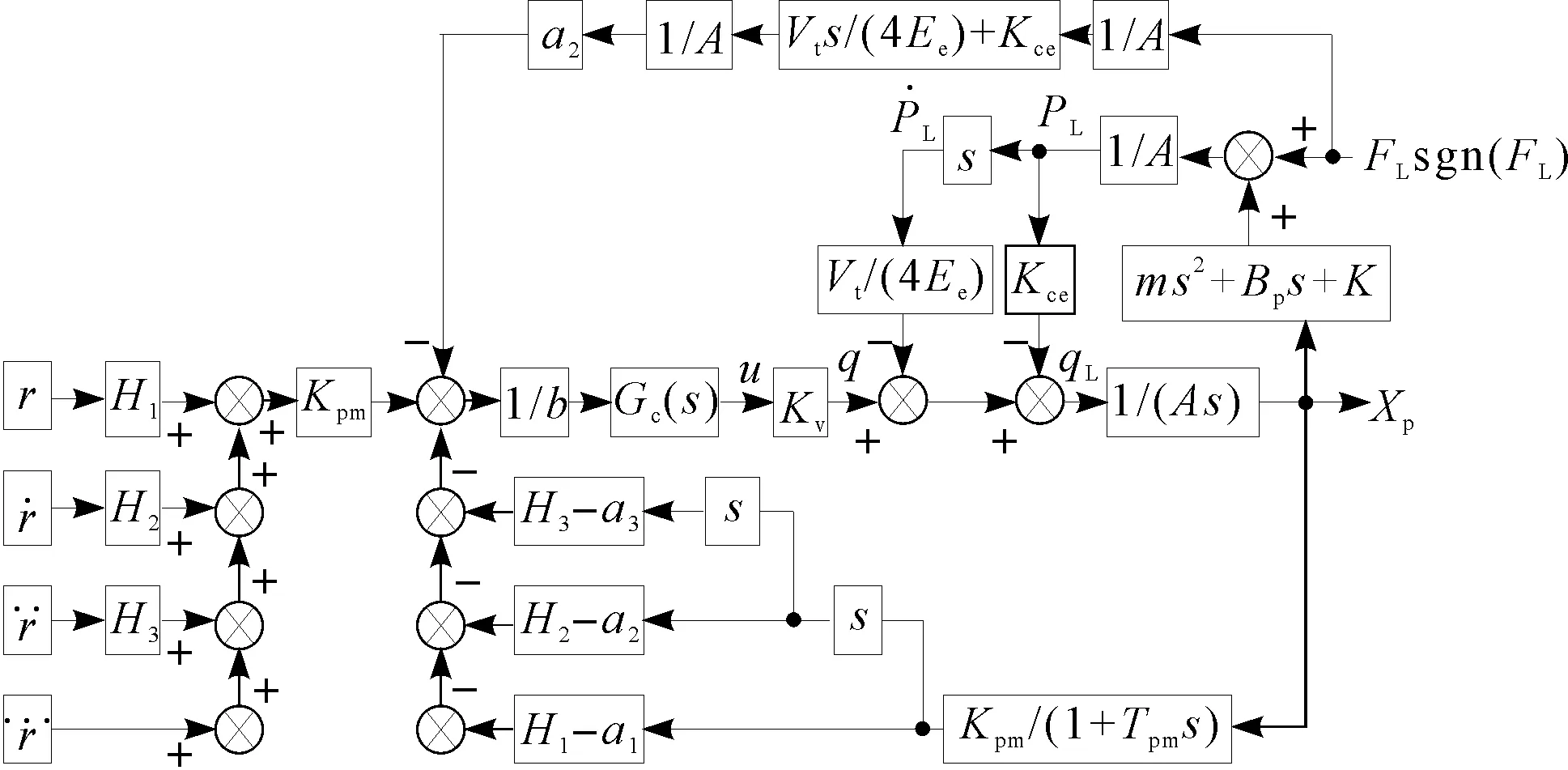
图3 基于Lyapunov直接法的系统控制框图
H1=CJ;H2=L+2/J;H3=CJ2+CL2+1/J
由式(16)可知,嵌入项可以分为两部分,即U=U1+U2,其中:

(18)
U2=b-1[a1x1+(a2-H2)x2+(a3-H3)x3]
(19)
下面讨论U1和U2的实现:
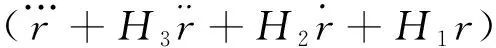
U2部分由可调液阻和一阶的弹簧阻尼系统组成,此部分控制律以实物方式实现,更有利于工程应用。这里,称U2为与动力机构并联的带可调液阻机液补偿器(以下简称为机液补偿器)。
以位置系统的输出位移Xp为输入,进出机液补偿器的流量Q0为输出,机液补偿器的传递函数可表示为:
G0=Q0/Xp=Cc(Bp0s+K0)(Vt0s/4Ee+Kce0)/A0=
Cc[Bp0Vt0s2/4Ee+(K0Vt0/4Ee+Bp0Kce0)s+K0Kce0]/A0
(20)
式中:Bp0—机液补偿器的粘性阻尼系数;K0—机液补偿器的弹簧总刚度;Vt0—机液补偿器的有效容积;A0—活塞有效面积;Kce0—机液补偿器的总流量-压力系数;Cc—可变液阻的液导。
设计机液补偿器时,需要根据下式以选取合适的弹簧刚度K0、有效容积Vt0、可变液阻的液导Cc和活塞有效面积A0,即:
(21)
加入机液补偿器后的系统控制框图如图4所示。
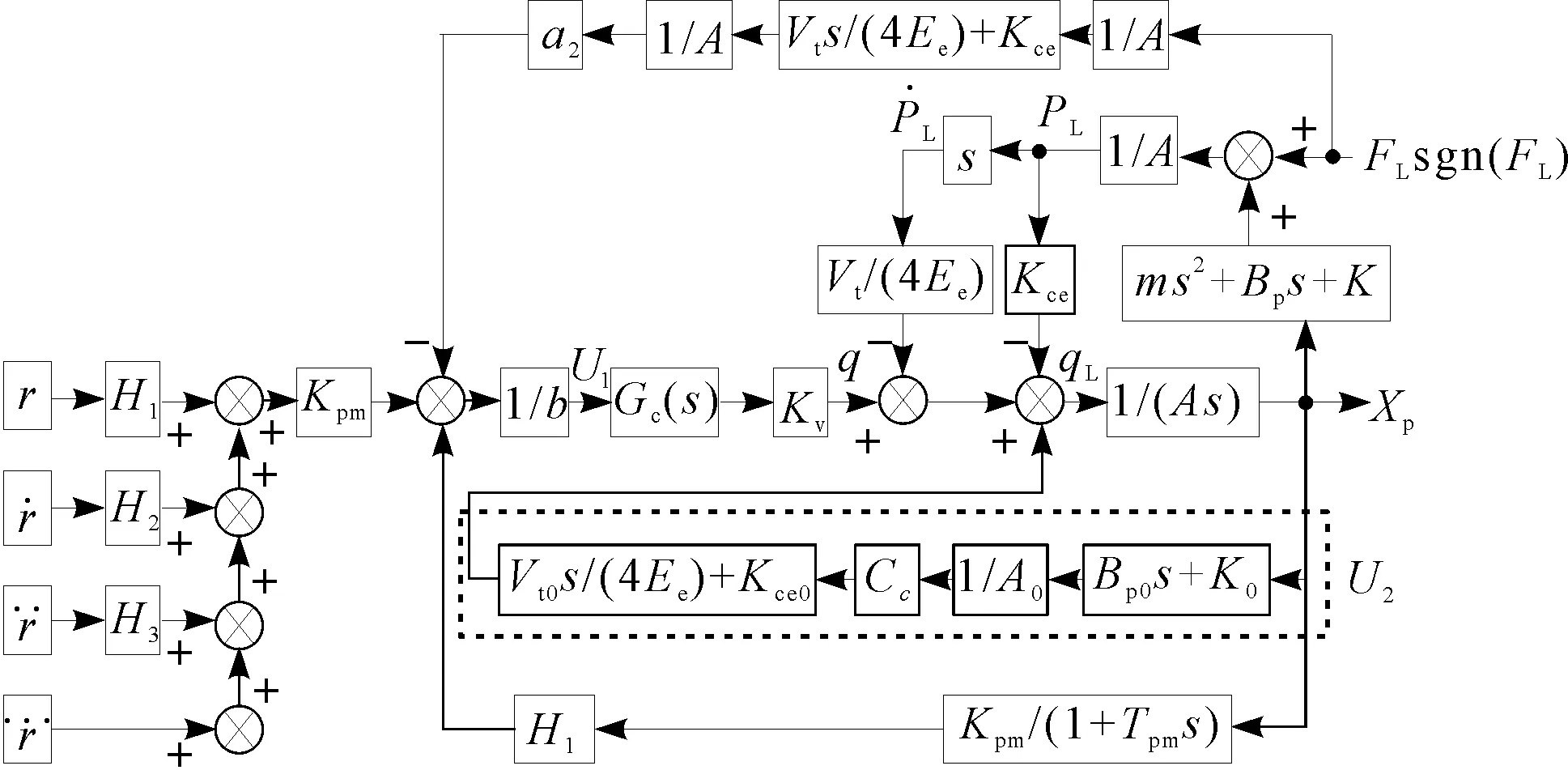
图4 加入机液补偿器后的系统控制框图
从图4可以看出:U2通道为负反馈,其作用点在qL处,与Kce一起直接增强了系统阻尼;通过调节可变液阻的液导,可提高系统的整体阻尼,系统的稳定性得到了改善,间接削弱了超越负载对系统的影响。
由于参数多,实现起来有困难,需要对式(16)进行必要的简化。
笔者选用文献[18]中的系统参数,其具体参数如表1所示。

表1 系统参数

(续表)
取系统负载刚度为K=1.2×105N/m,根据系统参数值求取式(16)的各项系数值,如表2所示。

表2 式(16)的各项系数值
由式(8)可知:
(1)系数a1中,R1表示惯性力的变化导致油液压缩对活塞速度的影响,其数量级为10-6;
(2)系数a2中,R31表示活塞速度,其数量级为1;R32表示粘性力导致油液泄漏对活塞速度的影响,由于阻尼系数远小于负载质量,其数量级远小于R21;R33表示弹性力的变化导致油液压缩对活塞速度的影响,其数量级为10-4,因此a2中起主导作用的是惯性力引起的泄漏流量与惯性力变化引起的压缩流量的比值,即R31/R1;
(3)系数a3中,R21表示惯性力导致油液泄漏对活塞速度的影响,其数量级为10-4;R22表示粘性力的变化导致油液压缩对活塞速度的影响,其数量级为10-9,因此a3中起主导作用的是引起活塞运动的流量与惯性力变化引起的压缩流量的比值,即R21/R1。
故式(9)中,系数a1、a2、a3可以简化为:a1=R4/R1=
4KKceEe/(mVt),a2=R31/R1=4EeA2/(mVt),a3=R21/R1=4KceEe/Vt。
上述参数的数量级经过比较化简后,由式(19)的方程可以得到实物实现方案,如图5所示。

图5 并联结构机液补偿方案
机液补偿器与位置系统并联安装,进、出油路分别与阀控缸的进、回油腔相通。
5 仿真与讨论
为了讨论方便,这里将笔者提出的控制策略,包括前向通道串联微分补偿器U1和机液补偿器U2两部分合在一起,称为复合控制;利用表1所示参数,对该控制策略进行仿真,并将其结果与带动压反馈环节的PID控制结果进行对比。
这里笔者选择仿真软件为MATLAB/Simulink,采用ode23s变步长算法,并取最大步长为1×10-5s,计算相对误差为1×10-6。
笔者在未校正、加入动压反馈环节,采用复合控制策略下,对位置系统的Bode图分析可知,系统采用复合控制策略后的幅值裕度为45.6 dB,相位裕度为88.9°。将该结果与加入动压补偿环节的系统进行比较(幅值裕度为36.6 dB,相位裕度为89.9°),可知该系统的稳定性更强。
选取控制器参数如下:
H1=3.5×107,H2=3.3×105,H3=450,b=9.07×105,Gc=1,取负载刚度K=1.2×105N/m,可调液阻Cc1=Cc2=Cc=1.06×10-12m3/(Pa·s);PID控制器参数取Kp=8,Ki=0,Kd=0;输入指令位置信号r=0.01 m;外负载力为恒值力FL=1 000 N。
采用复合控制策略后,系统与原系统的阶跃信号响应特性如表3所示。
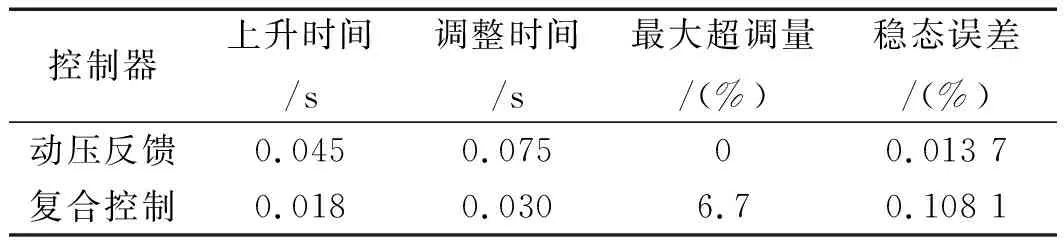
表3 系统响应特性
由表3可知,在采用复合控制策略后,系统达到稳定状态的时间明显缩短,可在0.02 s内达到稳态,并且系统的稳态误差小于0.108 1%,最大超调量为6.7%,由此可见,系统的动态性能有了明显的提高。
在相同条件和输入指令下,当外负载力以FL=14sin(6πt) kN的变化规律施加在位置系统上时,系统的响应曲线如图6所示。

图6 正弦外负载力作用下系统阶跃响应
图6中,由于正弦外负载力FL的变化率在一个周期内的绝对值变化呈由大到小再到大的趋势,而动压反馈环节起到的阻尼作用与FL的变化率成正比,即FL的变化率越大,动压反馈环节对FL的抑制作用越强,因此,当正弦外负载力达到最大值时,其变化率为0,动压反馈环节对FL几乎不起抑制作用。
笔者提出的复合控制策略的前向通道串联微分补偿器U1部分,考虑并补偿了FL及其变化率。由图6可知,复合控制策略在FL变化时具有很强的鲁棒性,系统的跟踪误差不超过0.37%,具有极好的跟踪精度。
在相同参数条件下,当活塞杆以0.001 m/s的速度运动时,外负载力FL在2.5 s内的规律变化如表4所示。

表4 外负载力FL取值
通过仿真得到的系统响应曲线如图7所示。
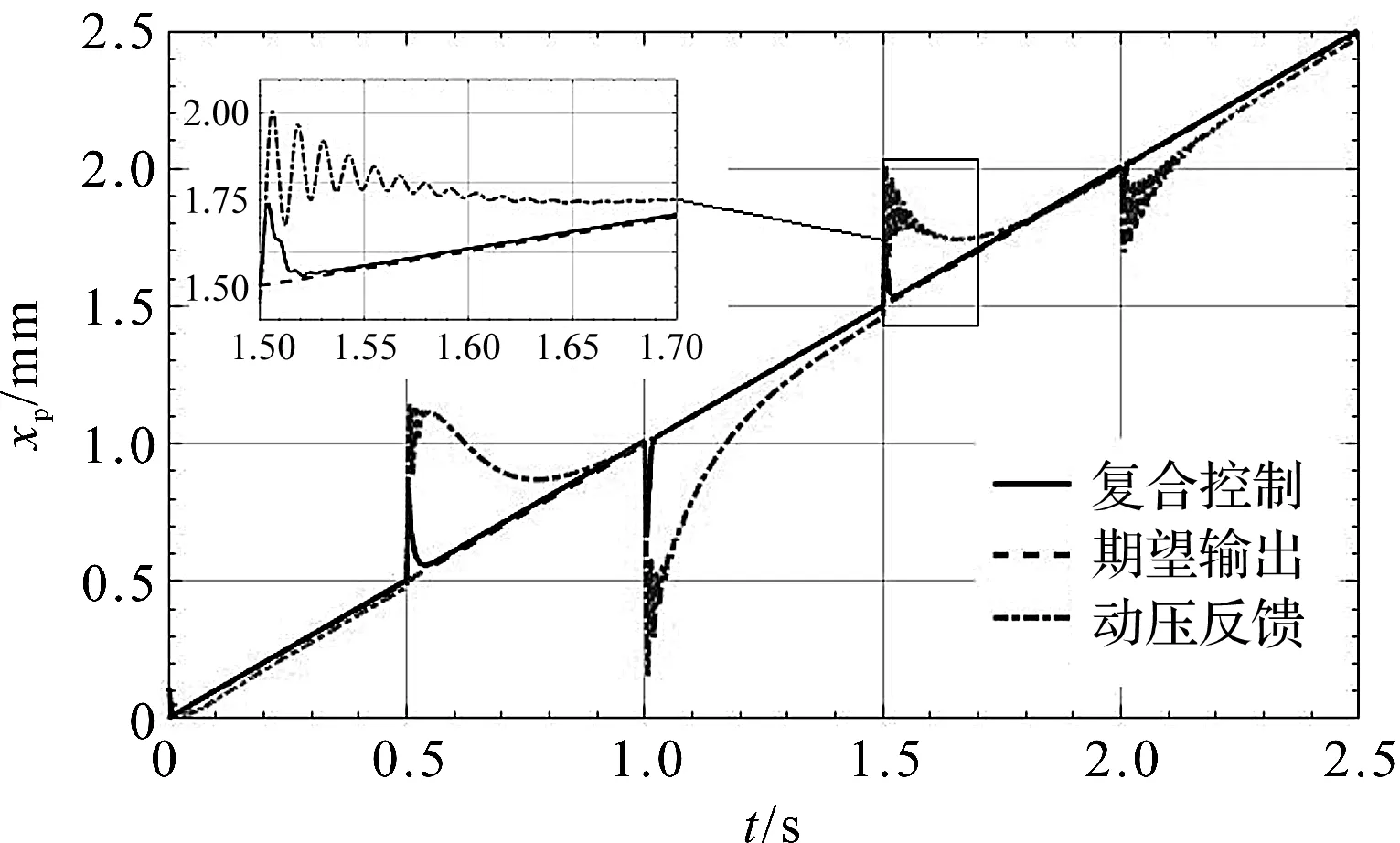
图7 正负交变负载作用下系统斜坡响应
在0.4 s~0.65 s内,液压缸两腔压力变化曲线如图8所示。
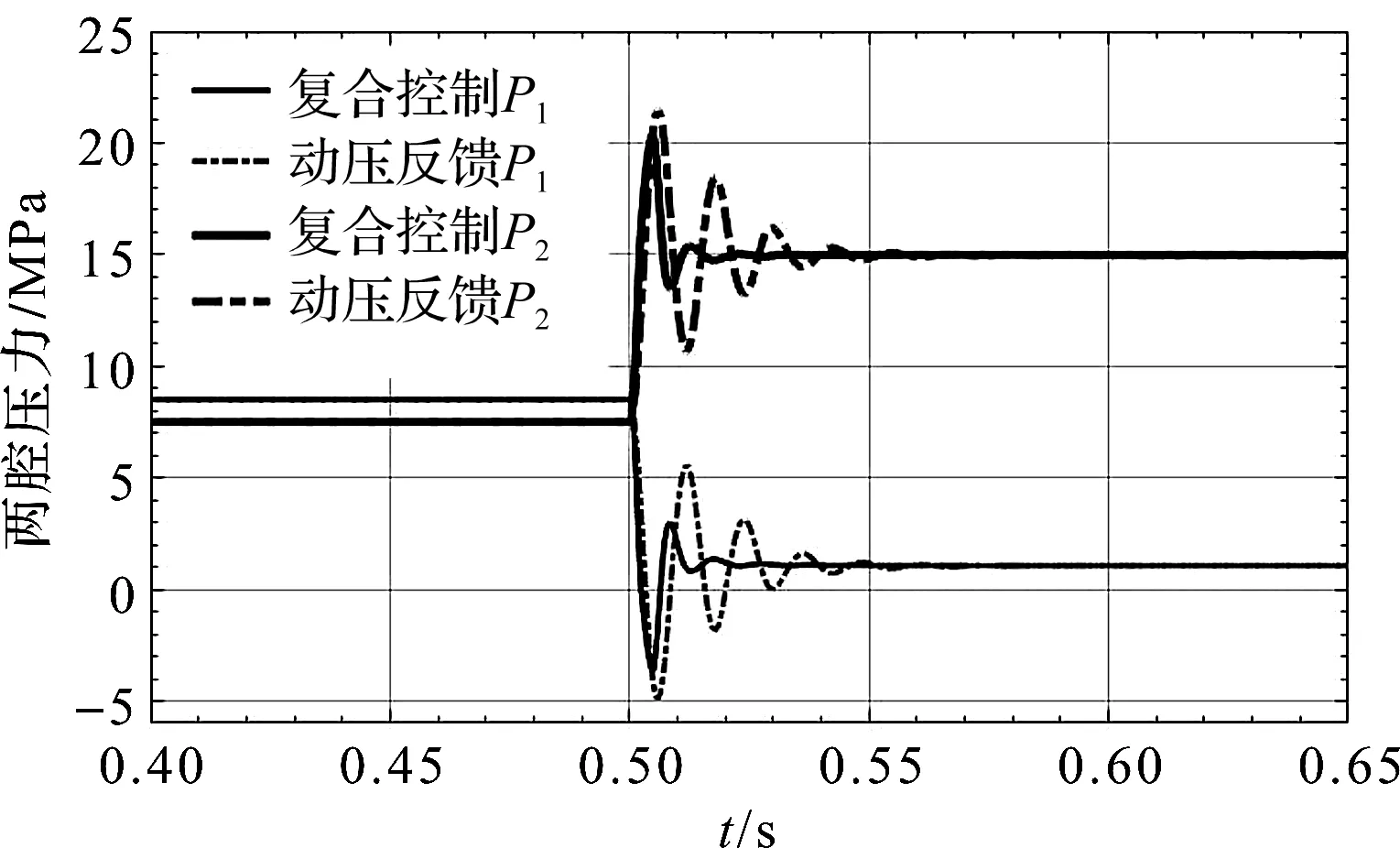
图8 液压缸两腔的绝对压力
由图(7,8)可知,在0.5 s~1 s和1.5 s~2 s两段时间内,系统处于超越负载工况,超越负载拖动活塞杆向右位移,导致回油腔即P2腔内产生附加的强迫流量,P2腔压力升高且强迫流量无法及时排出,此时系统动作不按指令运行;
采用复合控制策略后,伺服阀阀口快速开启,强迫流量通过阀口排出,进而液压缸P2腔压力降低,并在0.02 s内稳定;同时,P1腔补油充分,压力升高,两腔压差达到新的稳态值以平衡超越负载,速度稳定后的误差小于0.183%,表明系统对超越负载具有很好的鲁棒性。
6 结束语
在超越负载作用下,电液位置伺服系统的液压缸活塞会被迫运动,并出现强迫流量的现象,针对这一问题,笔者对系统的数学模型和强迫流量表达式进行了分析,得到以下结论:
(1) 根据电液位置系统工作原理,建立了系统的三阶非线性微分方程,采用Lyapunov直接法对系统稳定性进行了分析,通过Lyapunov直接法的反演方式求解了系统渐近稳定条件,给出了求取控制律的一般性方法;并构造了前向通道串联微分控制补偿器和与动力机构并联的带可调液阻机液补偿器,使所论控制方法得到了具体的实现;
(2)位置系统运行时,机液补偿器活塞杆与液压缸活塞杆同步运动,通过调节可调液阻的液导,可提高系统整体阻尼,系统的稳定性得到改善,有效削弱了超越负载对系统的影响。与动压反馈校正效果相比,系统在采用包含前向通道串联微分补偿器和与动力机构并联的带可调液阻机液补偿器的复合控制后,幅值裕度和相位裕度都得到了一定的提升,分别达到45.6 dB和88.9°;
(3)采用笔者所提出的复合控制策略后,系统空载时的稳态误差小于0.01%;在外负载力正负交变的条件下,所设计的控制律能根据容腔体积和活塞速度的变化,及时、有效地排出强迫流量,使系统能在0.02 s内达到稳态,稳态误差小于0.183%,相较于动压反馈校正,采用笔者所提出的控制策略,系统由超越负载引起的误差非常小,不会出现液压缸动作对指令信号的跟踪不连续现象;且在外负载力变化时具有很强的鲁棒性,系统响应更快、动态性能更好。
