高等数学中数列极限的求解方法

梁新峰，任丹丹

（安徽理工大学数学与大数据学院，安徽淮南232001）

数列是大学高等数学、数学分析及数学专业相关专业课程的基本知识点。它在大学的数学学习过程中起到了重要的作用。通过对数学分析和高等数学等课程的分析可知，数列极限不仅与函数极限密切相关，而且为学习定积分的定义、级数理论及离散数学等提供了极为重要的准备知识。另外，在“新工科”的背景下，我们秉承“传道授业解惑”的宗旨，树立和明确研究目标，更加注重对数列求解的方法创新及其对方法的分类。鉴于此，我们着重研究数列极限的求解方法及其分类。

函数是由定义域、对应法则及其值域所决定的，而数列是一类以正整数集（或者它的子列）为定义域的特殊函数。鉴于此，我们可以从函数的角度研究数列的结构性质。数列根据其不同的结构性质可分为有穷数列和无穷数列、周期数列、常数列等。因此，我们可以依据数列自身的结构性质采用不同的求解方法。

下面我们对数列收敛性的求解方法进行系统的研究。

1 数学归纳法

数学归纳法是一种基础的数学证明方法，通常用于证明与自然数N有关的命题成立，它主要用来研究与正整数有关的数学问题。故我们可以利用数学归纳法证明和求解某些特定数列的极限。解题过程通常分为两步，首先通过数学归纳法证明数列的极限是存在的，在此基础上，利用等式两端同时取极限、求解方程等方法求解数列的极限。

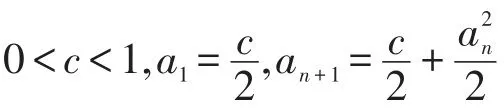
2 变量替换法

当已知两个数列中某些项之间的关系式时，直接证明两个极限均收敛往往是比较困难的。我们常常需要依据原有的关系式选取合适的中间变量，将原有的关系式化简，以便证明极限收敛。这样既可以简化我们的计算过程，又可以降低我们的解题难度。

3 函数极限法

数列是一种以正整数或者其子列为定义域的特殊函数。对于特定的较为复杂的数列，我们依据数列自身的结构及其关系式难以直接得到其极限。鉴于数列和函数之间的特殊关系，结合子列的收敛性和数列的收敛性的关系，我们可以将间断的数列的极限转化为对应连续函数的极限进行研究探讨。

4 定积分法

定积分是高等数学和数学分析等课程中重要的知识点，其在求解图形面积和物体质量等现实问题中起到了至关重要的作用。我们注意到定积分的定义是通过“分割、近似、求和及取极限”等4个步骤给出的。在此过程中，取极限是至关重要的一步，此步将烦琐的求极限的过程转化为定积分的求解过程。

5 利用微分中值定理法

在方法3中，我们注意到函数和数列之间的关系，如果数列对应的函数在特定的闭区间内是连续且可导的，则我们可以利用连续函数在闭区间内的结构性质（如拉格朗日中值定理、柯西中值定理等）研究数列的结构性质。下面我们利用函数的微分中值定理将例1重新证明，以此说明此法在研究数列收敛中的作用。

6 利用施笃兹公式进行求解

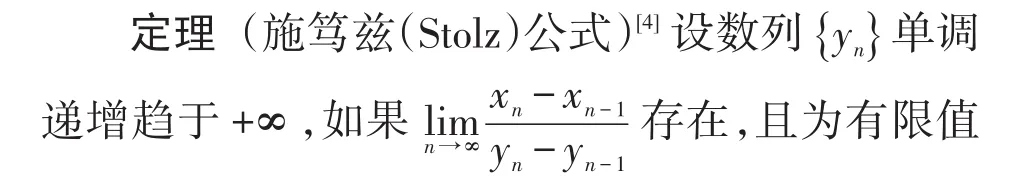
6 结束语

本文阐述了数列在大学数学学习中的重要性，并基于此，对研究数列收敛的方法进行了较为全面的分类和阐释，包括数学归纳法、变量代换法、积分法、利用微分中值定理和施笃兹（Stolz）公式等。