基于改进Dijkstra 算法的进路搜索研究
2020-11-04杜文文
杜文文,杨 扬
(西南交通大学 信息科学与技术学院,成都 611756)
进路处理是计算机联锁系统的核心功能,进路搜索的主要目的是便于进路处理。目前,已有多种进路搜索研究方法,如广度优先[1]、改进深度优先[2]及其它启发式算法[3]等。Dijkstra 算法是一种较为成熟的最短路径算法,其典型应用是解决距离最短、时间最少和花费最低的问题[4]。但传统Dijkstra 算法求解最短路径会耗费大量存储空间和计算时间,易陷入局部最优[5]的问题。为减少搜索深度,本文提出一种基于改进Dijkstra 算法的进路搜索算法。改进后的Dijkstra 算法效率高,且简单易读。
本文建立车站站场图简化模型,采用有向图描述站场拓扑结构;在数据存储结构和优先级队列2个方面,对传统Dijkstra 算法进行改进,采用广度优先的搜索方式,并编制仿真程序验证将改进Dijkstra算法用于进路搜索的有效性。
1 站场拓扑结构的有向图建模
有向图由顶点集和连接任意2 个顶点之间的边集组成,顶点集表示数据元素的集合,边集为连接2 个顶点之间的指向关系[6]。将铁路站场图抽象为有向图,站场进路搜索问题即可转化为有向图的遍历问题[7]。
站场进路搜索具有方向性。在搜索过程中,先确定好进路起始和终止信号机,从起始信号机到终止信号机之间经过的路径称为搜索进路,一条完整进路包含进路类型、方向和道岔信息等相关内容[8]。完成进路搜索后,将搜索结果保存为文件,以便于进路处理。
图1 为某铁路站场平面布置图。由图可知,铁路车站信号设备之间有前后连接关系。为了建立站场模型,对站场设备进行简化,抽象定义为不同属性的信号设备,主要考虑轨道电路、道岔和信号机3 种设备。道岔和信号机作为顶点,轨道电路作为边,尽头线和安全线则以相连的道岔或信号机设备作为顶点,整个站场设备的拓扑结构可抽象为一个网状结构[8]。
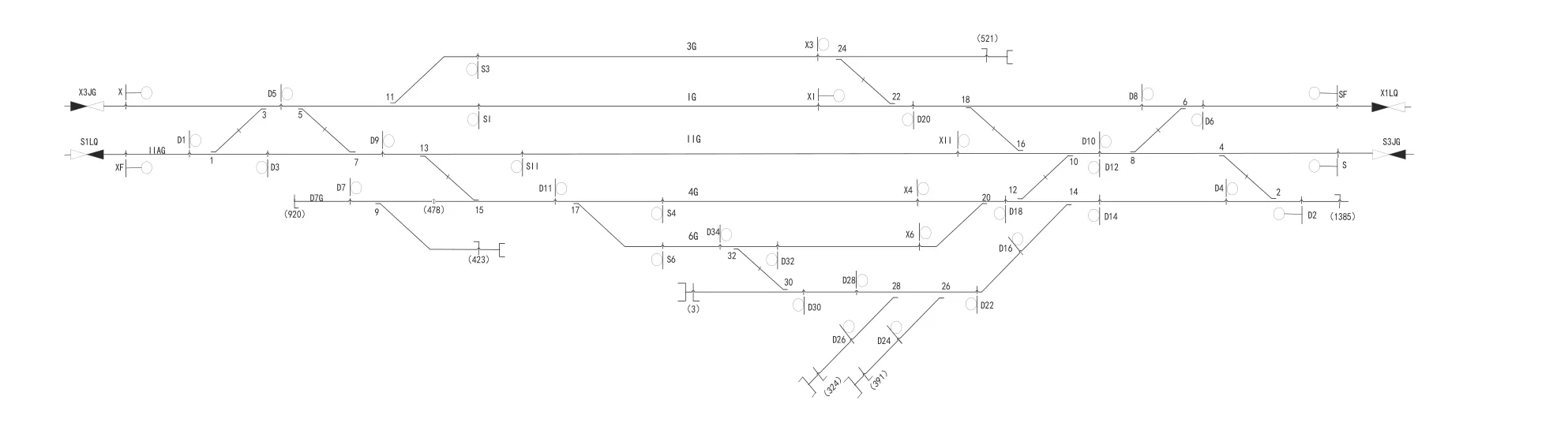
图1 某铁路站场平面布置
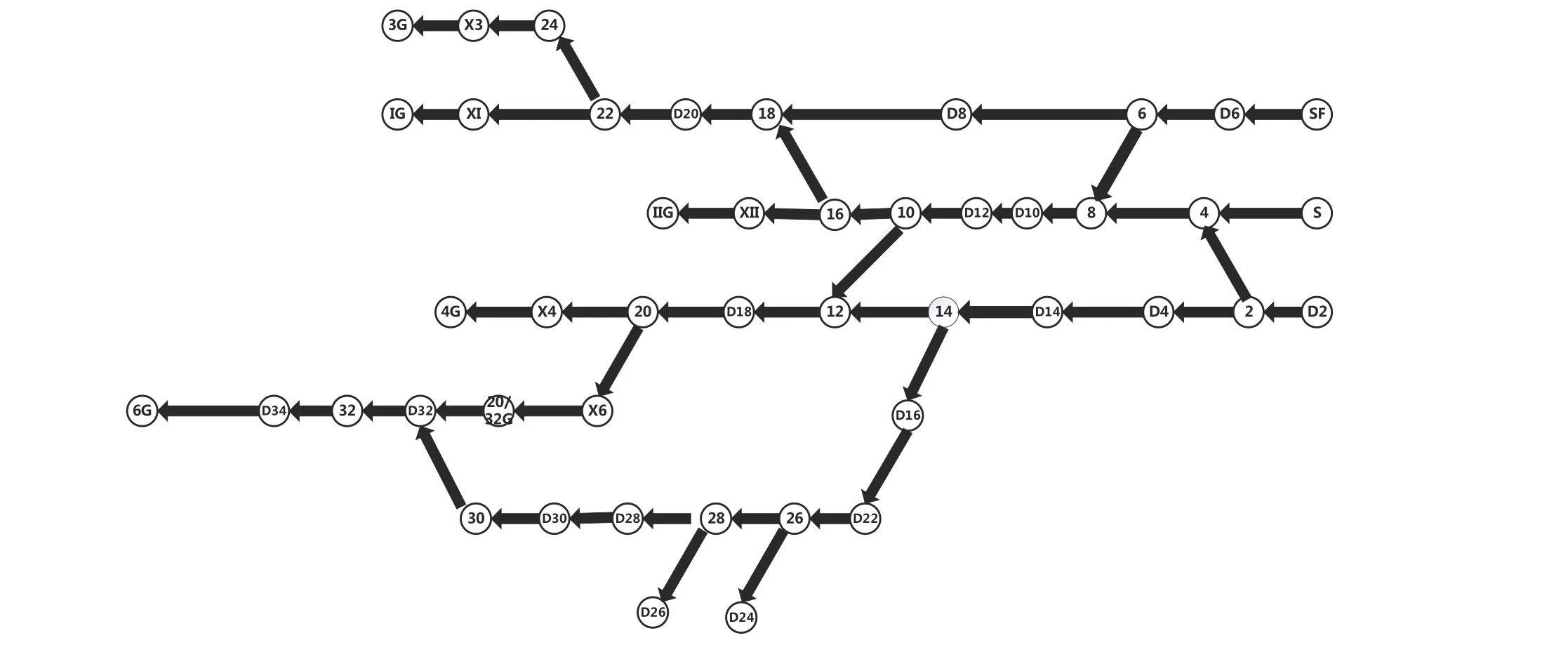
图2 某铁路站场局部有向图模型
2 Dijkstra 算法的改进
2.1 传统Dijkstra 算法
Dijkstra 算法是经典的最短路径算法,用于计算正权图的单源最短路径,即对于给定源节点,可求解自起始节点到其它所有节点的最短路径[9]。最短路径不仅指传统意义上的距离最短,也可定义为代价最低,主要用于路网规划、旅行商问题、公交车线路规划以及社会能源分配等方面[10]。最短路径模型可以描述为:表示s到t的最短路径;其中,i与j表示s到t这条路径上的中间节点;D(i,j)表示i到j的最短路径。
在实际应用中,传统Dijkstra 算法主要存在3 个不足之处[11]:(1)若数据存储采用邻接矩阵,对于大型稀疏矩阵会造成空间浪费,计算时间代价也高;(2)在算法迭代过程中,若节点所在链表或数组是无序的,每次搜索都将遍历全部节点,会影响搜索效率;(3)不适用于解决节点数目庞大的问题。
2.2 优化方法
针对传统Dijkstra 算法存在的不足,结合铁路站场结构特点,从数据存储结构和队列结构2 个方面改进Dijkstra 算法。
2.2.1 存储结构优化
Dijkstra 算法有2 种应用广泛的数据存储结构:邻接表和邻接矩阵。其中,邻接矩阵会浪费大量存储空间,时间复杂度更高,而邻接表可有效节省存储空间[11]。邻接表通常采用链表存储,而站场图拓扑结构较为简单,每个节点的相邻节点一般仅为1~3 个。若采用链表实现,程序设计相对复杂,因此使用数组存储。程序设计中用2 维数组来实现,数组每1 个元素均为global_Node_Adj 类型,数据结构定义如表1 所示。

表1 邻接表数据结构定义
2.2.2 队列结构优化
对于传统的Dijkstra 算法,依次在节点集中查找未遍历过的节点、寻求最优解的过程会极大地影响算法效率。为减少这种影响,采用优先队列(priority_queue)对节点集进行有效排序,使插入或修改数据后,节点集仍能保持有序性。
优化队列结构采用堆栈,以优化每次查找离起始节点最近的节点的时间复杂度,而邻接表能够有效改善邻接矩阵占用过多空间的问题,减少存储空间的占用。
3 算法设计
3.1 进路搜索策略
对于进路搜索问题,确定好进路的起始节点和终止节点后,如何快速有效地选择一条最优路径是关键。当遇到对向道岔节点时,结合站场有向图拓扑结构的特点,若能避免迂回进路,则可以大幅提高运行效率[12]。搜索策略主要有广度优先搜索和深度优先搜索;深度优选搜索是根据节点查找其邻接节点的过程,而广度优先搜索则是根据边查找其邻接点的过程。根据改进Dijkstra 算法的特点,需要优先确认边的信息,故采用广度优先搜索更为方便。
除考虑距离因素外,本文设计的进路搜索算法还考虑了路径经过的道岔数目。理论上,搜索进路时存在多种遍历选择,因此会产生多条搜索路径。为尽量少占用轨道设备资源,少搜索分支,设置一个关键条件—搜索路径上道岔节点数量较少;同时,在道岔节点数量一致的情况下,选择列车进路作业用时最少的路径,即最短路径。改进Dijkstra 算法中,对边进行松弛操作是根据目标函数值,目标函数值为:

其中,α、β为权重系数,两者之和为1;C是常量,其目的是考虑到道岔数与距离存在数量级差,故在将道岔数目放大一定比例的基础上,合理分配权重。
3.2 变量及数据结构定义
改进Dijkstra 算法使用广度优先搜索解决赋权有向图单源最短路径问题,最终得到一棵最短路径树。在Visual Studio 2019 IDE 中,采用C++编程语言实现进路搜索算法,将生成进路的相关数据存放于AllPathForRead.csv 文件。建立Matlab GUI 界面,通过MEX 文件实现C++与Matlab 的接口,在起点和终点文本框中输入相应节点时,Matlab GUI 通过回调函数自动遍历找到搜索路径。
自定义的站场图数据格式如表2 所示,存储为CSV 格式文件,包含起点字符串、起点类型、终点字符串、终点类型、距离。其中,起点、终点字符串为信号设备名称,类型为自定义,默认信号灯类型为1,道岔节点类型为2。
表3 是根据输入CSV 重新生成的边数组,在表2 基础上,每个节点增加了数字索引,便于程序读取。
定义一个Dijkstra_Node 结构体数组,其代码框架如图3 所示。该结构体包含当前点m_cur_node、父节点m_parrent_node、是否访问m_is_visited、距离m_ditance、访问标志、距离、道岔数、目标函数值。
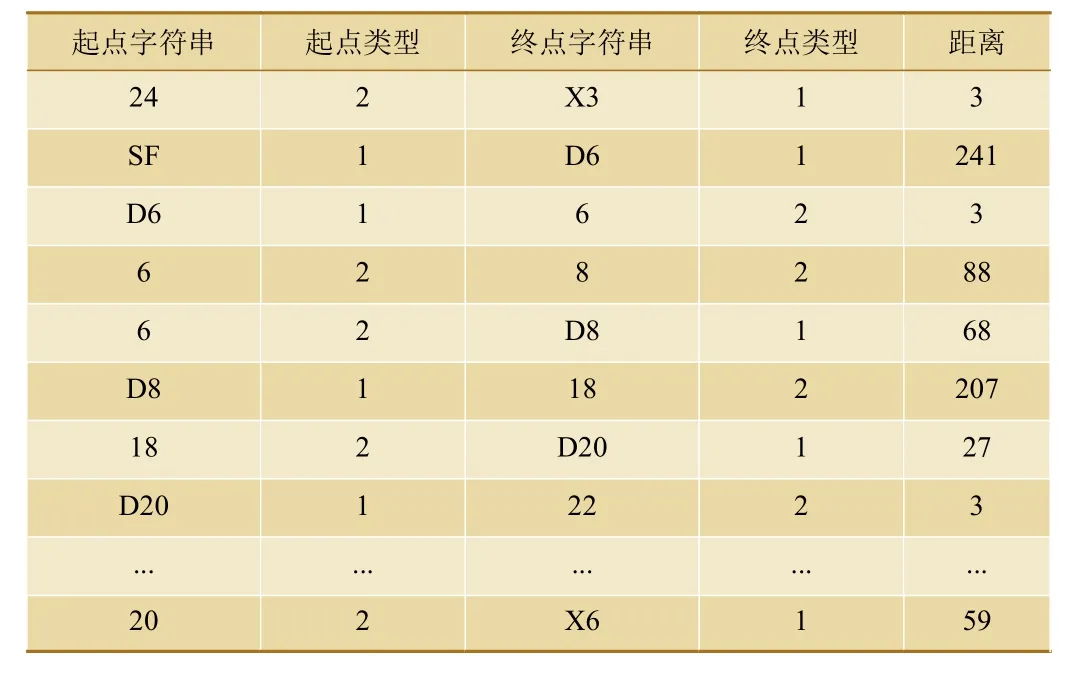
表2 站场图CSV 数据格式
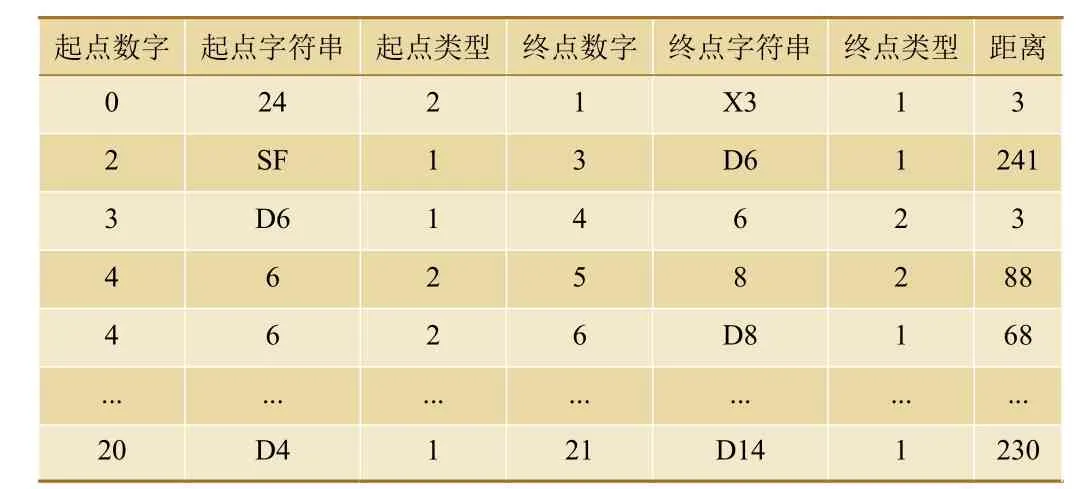
表3 站场图边数组格式
其中,访问标志用于判断当前节点是否已被访问,若该节点已被访问则退出,进入下一循环;若未访问,则需要先将此节点的访问标志设置为已访问,再去访问该节点的邻接点。m_distance 为源节点到当前节点的距离,m_turnout_node_num 为源节点到当前节点所经过的道岔数,m_f_weight_sum 为源节点到当前节点的目标函数值。
当前节点m_cur_node 是指能够与源节点连通的节点,而m_parrent_node 就是每条路径对应节点的父节点。在初始化时,父节点的m_name 被初始化为“NOT”,代表当前节点还没有父节点。是否访问标志m_is_visited 用于确定该节点是否能被确定为最佳目标值。在结构体中,对m_f_weight_sum 进行友元重载,其目的是后面优先队列出列时,以最小值为最高优先级,因为C++的优先队列默认是最大值先出列。
3.3 算法搜索流程
改进Dijkstra 算法中进路搜索的具体流程为:
(1)定义元素为Dijkstra_Node 的优先队列,初始化Dijkstra_Node 数组信息;
(2)将源节点的目标值设置为0,并将该节点压入优先队列,判断队列信息是否为空;若为空,跳至(6);
(3)队列信息不为空,则保存源节点信息,并根据边的指向,搜索下一个节点(即源节点的邻节点);
(4)获得源节点到邻节点的距离和道岔数,计算目标值并进行判断,将目标值较小的邻接节点设置为目标节点;
(5)依据判断结果保存目标节点信息,更新Dijkstra_Node 数组,将目标节点作为源节点搜索下一节点,返回(3);
(6)结束遍历,返回初始化Dijkstra_Node 数组信息。
4 实例仿真分析
进路按结构特点可分为有环和无环2 类,无环进路为单路径直股搜索,有环进路又可分为多路径直股搜索和弯股搜索。
采用改进Dijkstra 算法,对3 种类型进路进行搜索验证,并利用MATLAB GUI 实现路径搜索结果的可视化。
4.1 单路径直股搜索
以D14—D28 进路为例,这条路径不包含八字道岔,不存在迂回进路,即有且只有1 种路径选择。结果显示进路X—SI 搜索到的最优路径为:D14—14—D16—D22—26—D28,路径长度为335 m,道岔节点数为3,目标值为328,如图4 及图5 所示。
4.2 多路径直股搜索
以SF—XI 进路为例,其起始和终止信号机均在同一股道上,但这2 条进路均包含八字道岔,在搜寻过程中可有多条路径选择。以SF 为始端,XI 为终端,可有2 种路径选择:

图4 D14—D28 进路搜索设置与结果显示界面
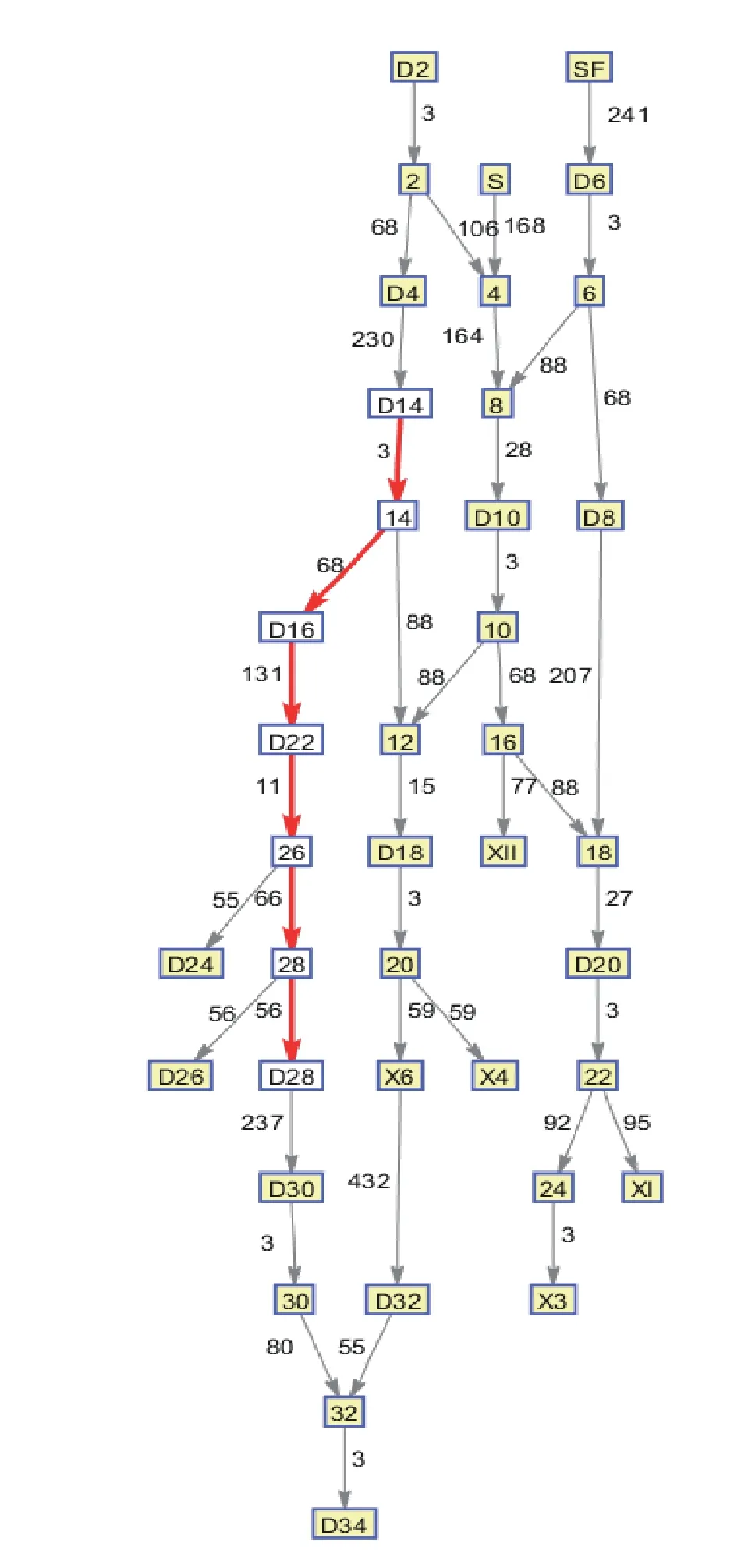
图5 D14—D28 进路搜索路径
(1)SF—D6—6—D8—18—D20—22—XI
(2)SF—D6—6—8—D10/D12—10—16—18—D20—22—XI
其中,路径(1)搜索到的道岔节点为3,路径(2)搜索到的道岔节点为5,路径(1)上道岔点节更少,且其长度小于路径(2),因此路径(1)为最优选择。采用改进Dijkstra 算法,搜索到的最优进路为路径(1),路径长度为664 m,道岔节点数为3,目标值为575.2,结果如图6 及图7 所示。

图6 SF—XI 进路搜索设置与结果显示界面
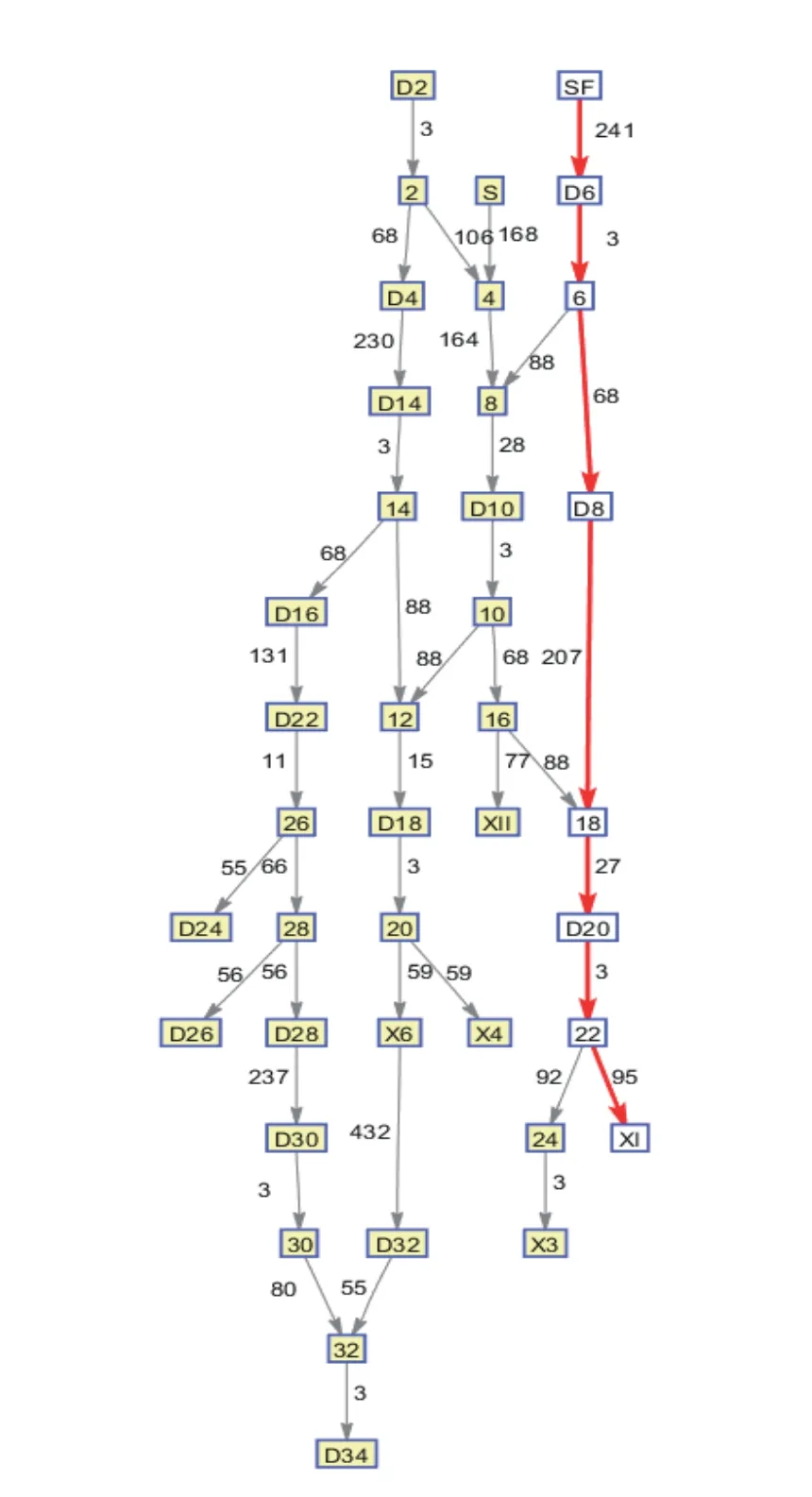
图7 SF—XI 进路搜索路径
4.3 弯股搜索
以D2—D34 为例,对于多路径选择的情况,先考虑少搜索分支,比较搜索路径上道岔节点数目。若道岔节点数目相同,再考虑路径最短的进路,使用改进Dijkstra 算法进行进路搜索,以寻找最优路径。结果如图8 及图9 所示。

图8 D2—D34 进路搜索设置与结果显示界面
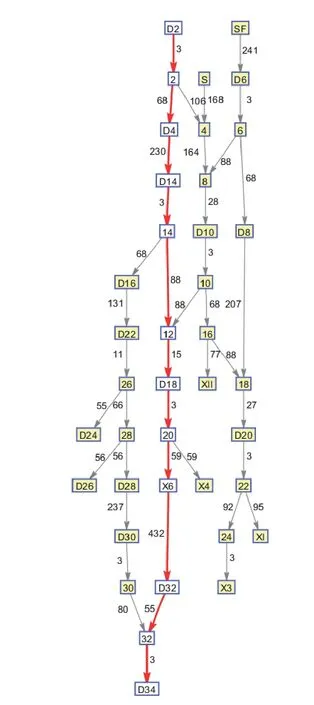
图9 D2—D34 进路搜索控制台
以D2 为始端,D34 为终端,其路径选择有:
(1)D2—2—D4—D14—14—12—D18—20—X6—D32—3—D34
(2)D2—2—D4—D14—D16—D22—26—28—D28—D30—30—D32—32—D34
(3)D2—2—4—8—D12—D10—10—12—D18—20—X6—D32—32—D34
其中,路径(1)搜索到5 个道岔节点,路径(2)搜索到5 个道岔节点,路径(3)搜索到7 个道岔节点;因此,路径3 被剔除。剩下的路径(1)和路径(2)考虑最短路径,搜索结果为:Path=D2—2—D4—D14—D16—D22—26—28—D28—D30—30—D32—32—D34,路径长度为959 m,道岔节点数为5,目标值为867.2;结果如图8 及图9 所示。
以上3 种类别进路搜索的实验结果表明:改进Dijkstra 算法可高效、正确地完成多种类别进路搜索,效果较为满意。
5 结束语
提出改进Dijkstra 算法,采用邻接表和优先队列的数据结构,以Viusal Studio 2019 为开发平台,在Matlab GUI 中通过接口进行调用,实现铁路站场进路搜索不重复、不遗留。该算法应用于进路搜索的优点主要有2 个方面:(1)算法程序与站场数据相互独立,遍历不同的站场图只需修改站场数据即可,程序可移植性强;(2)算法设计提高了内存空间利用率,缩短了搜索时间,提高了站场图遍历效率。
