超声速可压缩火焰面模型的研究进展
2020-11-04高振勋蒋崇文李椿萱
高振勋,蒋崇文,李椿萱
(北京航空航天大学 国家计算流体力学实验室,北京 10019)
0 引 言
超燃冲压发动机的发展令超声速湍流扩散燃烧的数值模拟技术受到了高度重视[1-3]。基于雷诺平均(RANS)以及大涡模拟(LES)方法对湍流燃烧流动进行数值模拟时,不可解尺度上发生的湍流与燃烧化学反应相互作用过程需要湍流燃烧模型考虑[4-7]。事实上,目前的湍流燃烧模型主要考虑的是湍流脉动效应对燃烧过程的影响,而燃烧放热效应对湍流的影响则主要通过可解尺度上流场参数的变化来反映[8-11]。目前国外已发展了多种湍流燃烧模型,包括火焰面模型[12-13]、条件矩模型[14-15]、线性涡模型[16]、输运PDF模型[17]等,而本文主要关注其中的火焰面模型。
火焰面模型是基于燃烧化学反应时间尺度足够小的假设而建立的,该模型并不对组分输运方程中的时间平均(RANS)或滤波后(LES)化学反应源项进行封闭,而是直接对反应标量(组分浓度和温度)进行模化。该模型利用混合分数变量,将不可解尺度上的火焰内部结构模拟与可解尺度上的湍流混合模拟从形式上解耦。火焰内部结构可通过求解在混合分数空间内基于渐近分析得到的火焰面模型方程得到[18],湍流混合过程则由混合分数和标量耗散率的联合概率密度函数(PDF)描述。最后,通过PDF 积分则可完全确定湍流燃烧过程中组分浓度和温度的平均特性。由于使用该模型时不需要求解组分的输运方程,对于大规模化学反应系统的模拟该模型在计算量上具有明显优势。由于一般稳态火焰面模型中只利用火焰面模型方程的稳态解,因此无法考虑自点火和熄火过程,因此之后又进一步发展了火焰面/进度变量模型[19-21],该模型中所使用的火焰面数据库同时包括了火焰面方程的稳态和非稳态解,并且其控制变量变为混合分数和进度变量(选定的某组分浓度),同时该模型需要求解被选定作为进度变量组分的输运方程。总的来说,火焰面类模型在一定条件下才适用,其突出特点是计算量并不随化学反应系统增加而明显增大。
火焰面类模型最初均是针对低速湍流燃烧流动而建立的,模型中很多假设在超声速可压缩流动中并不成立,因此不能直接应用于超声速湍流燃烧流动。国内外部分学者已经开展了火焰面类模型向超声速湍流燃烧流动推广的相关研究,本篇文章主要目的是对该方面的研究进展进行综述,其中重点介绍本文作者所开展的相关工作。
1 火焰面类模型理论
1.1 火焰面模型
描述火焰内部结构的火焰面模型方程是在一定物理假设下得到的,其物理图像如图1所示。该模型假设燃烧的化学反应足够快,局部瞬时化学反应层的厚度(lr)小于湍流的Kolmogrove尺度(ηk),在该尺度下组分浓度和温度的湍流脉动已由分子黏性所耗散,因此化学反应层内部不受湍流脉动的影响,只由分子扩散控制。另外,大尺度湍流运动的应变率可引起化学反应层空间上的褶皱,但由于化学反应层厚度远远小于褶皱的曲率半径(约等于湍流积分尺度,如图1中的lt所示),以致组分浓度沿化学反应层切向的变化与沿法向的变化相比可以忽略。在以上假设基础上所建立的火焰面模型相当于将湍流火焰看作是嵌入在湍流流场内薄的具有一维结构的火焰面系综。
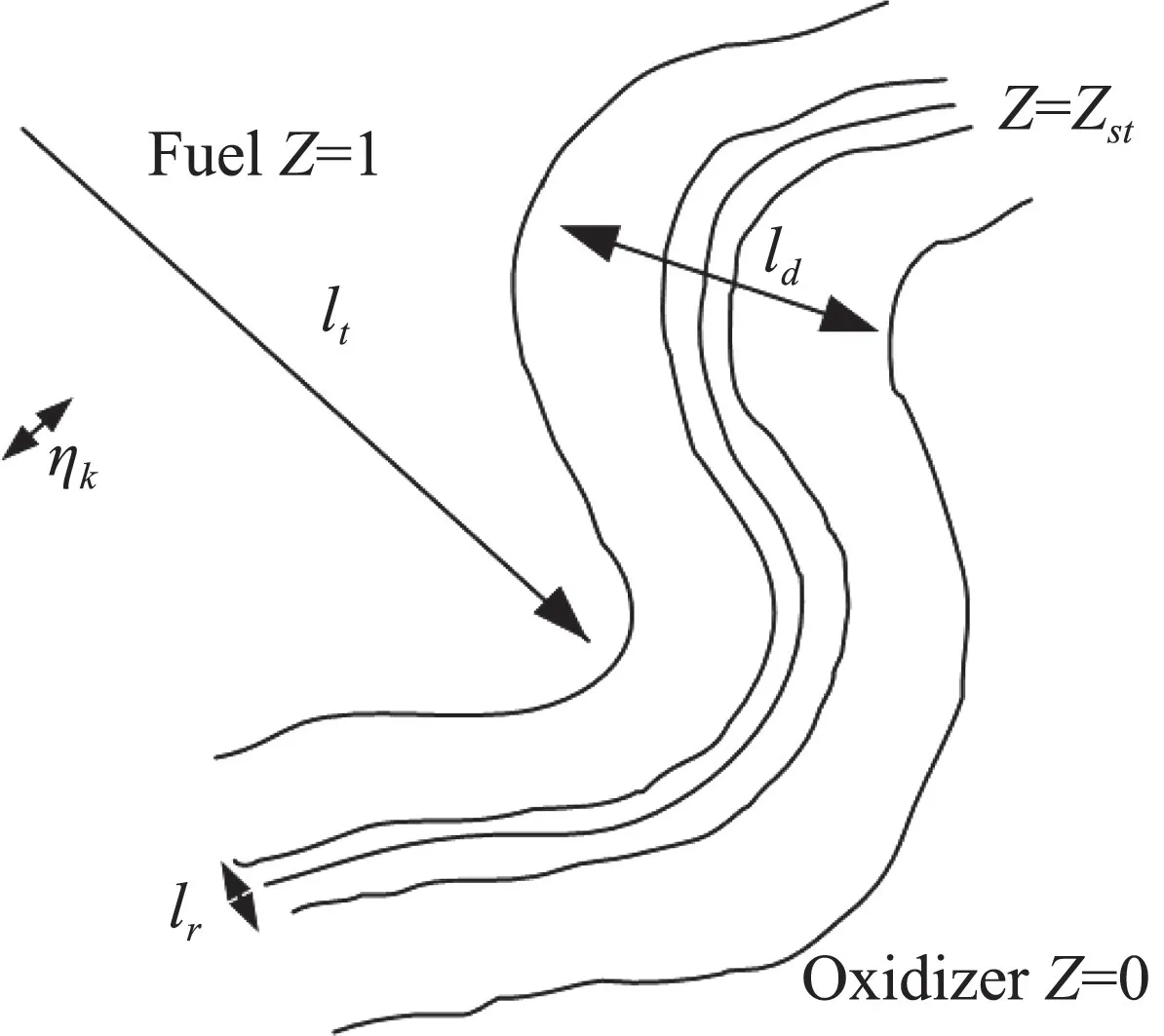
图1 火焰面模型的物理图像Fig.1 Physical image of the flamelet model
通过引入扩散燃烧中的重要物理量混合分数Z,可将瞬时组分浓度输运方程变换到混合分数空间,以混合分数空间内的化学反应层厚度作为小参数进行奇异摄动分析[18],忽略非定常效应,可得到火焰面内组分浓度的控制方程如式(1)所示,其中Ys为组分s的质量分数,ρ 为密度,χ 为标 量耗散率,为组分s的化学反应源项。另外,在低马赫数条件下,忽略静焓h 瞬时输运方程中的黏性耗散项及压力项,并在Lewis数为1的假设下,可得到瞬时静焓h 与混合分数Z 的方程相似,即式(2)中的h 和Z 的线性关系。最后,在低马赫数条件下假设整个燃烧空间为常压空间,即式(3)中的p 为常数。于是,可最终导出火焰面模型的控制方程为:
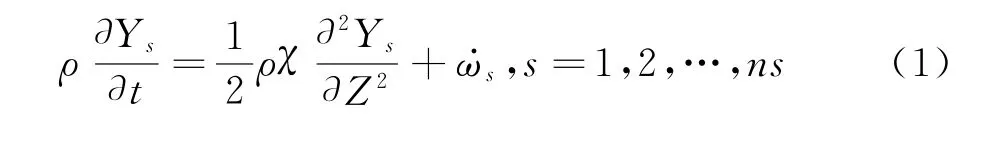
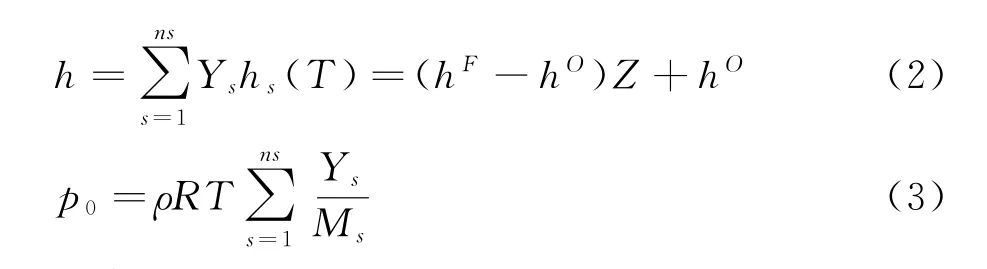
其边界条件为:
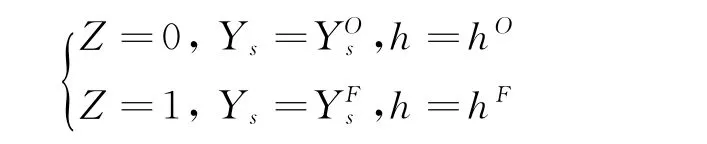
其中上标F 和O 分别表示燃料和氧化剂来流中的变量值。由于直接考虑火焰面模型方程中的非稳态效应难度较大,因此一般在应用时忽略式(1)中的时间相关项,此时称为稳态火焰面模型。式(1)中的标量耗散率χ 是随Z 变化的参数,一般采用当量混合分数Zst对应的χ 值,即当量标量耗散率χst,作为湍流混合场对火焰内部结构施加作用的控制参数。在给定不同的当量标量耗散率χst值条件下,求解火焰面模型方程(1)~(3)可得到Ys(Z,χst),T(Z,χst),即建立所谓的火焰面数据库。之后,流场内的平均组分浓度和温度可由PDF(PDF形式采用预设方式得到)积分获得:

基于随机变量Z 和χst分别与湍流的大尺度和小尺度相关的观点,可假设两者统计独立,则可表示为两个边缘PDF的乘积:

1.2 火焰面/进度变量模型
事实上,完整的火焰面模型方程的解包括稳态和非稳态两个分支,即所谓的“S型曲线”。以上稳态火焰面模型中以χst为控制参数建立的火焰面数据库只包含了稳态解,不能得到完整描述最大火焰温度与当量标量耗散率χst关系的整个“S型曲线”,从而无法模拟自点火和熄火过程。火焰面/进度变量(Flamelet/Progress Variable,FPV)模型[19-21]的提出主要是解决火焰面模型对自点火模拟精度不准确的问题,方法是引入一个可描述化学反应进程的进度变量C,以进度变量C 作为火焰面方程组的控制参数。C 可定义为某种反应物或生成物的组分浓度,由此可得:
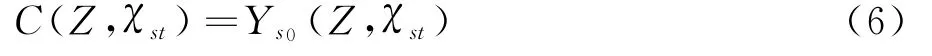
由于C 在χst一定的情况下与Z 一一对应,而其他组分浓度以及化学反应源项也与Z 一一对应,因此可以建立其他组分浓度以及化学反应源项与进度变量C 的一一对应关系,即建立包含Ys(Z,C)和关系的数据库。由此建立的火焰面数据库可以描述完整的“S型曲线”,从而准确描述自点火和熄火过程。
在获得火焰面数据库的基础上,可得到平均的组分浓度和温度在物理空间中的分布:

混合分数和进度变量的联合概率密度分布为:
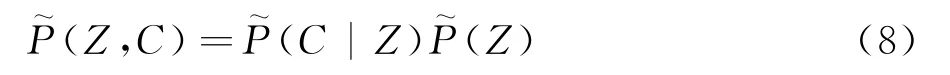


因此,还需要求解进度变量C 的输运方程,其中的进度变量源项的计算公式为:
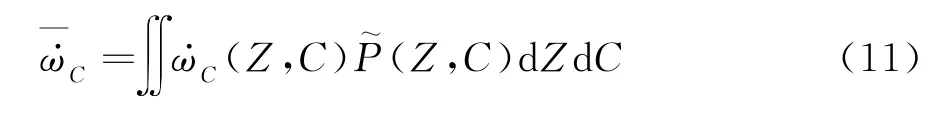
2 火焰面模型的可压缩修正
要将火焰面模型用于超声速燃烧流动中,首先面临的一个问题是:火焰面类模型中的基本假设——燃烧化学反应的时间尺度足够小而令局部瞬时化学反应层的厚度小于湍流的Kolmogrove尺度——在超声速燃烧流动中是否能够满足? Bray等[25]分析认为超燃冲压发动机燃烧室的燃烧满足火焰面的假设。Balakrishnan等[26]在湍流积分尺度等于燃烧室尺寸以及湍流度为50%的假设下,估计了来流马赫数1~25范围内超燃冲压发动机燃烧室内的湍流时间尺度的变化,并利用氢气/空气动力学模型估计了化学反应时间尺度,分析认为大部分情况下燃烧室内超声速湍流燃烧流动可满足火焰面假设。Waidmann 等[27]对德国宇航局(DLR)氢燃料超燃冲压发动机实验数据的分析也显示其燃烧处于火焰面模式。针对这一问题,国内Gao等[28]和Fan等[29]分别开展了典型氢燃料超声速燃烧室内湍流和燃烧特征时间尺度的分析,利用Cuenot给出的判据[30]检验火焰面假设在超声速燃烧流动中是否能够满足。其中,Gao等的分析基于RANS模拟,而Fan等则利用混合RANS/LES模拟,分析结果均显示,火焰面模型的基本假设在所研究的超声速燃烧场中均成立。然而,针对碳氢燃料的超声速燃烧流场中火焰面假设成立情况的研究,目前尚未见到公开文献报道。
在火焰面基本假设满足的条件下,火焰面模型在超声速燃烧流动中的应用还面临其他问题。原始的火焰面模型在使用时,流场的平均温度与组分浓度一样,均是由火焰面数据库的PDF积分获得,这种方法在超声速流动中无法考虑温度与速度的强耦合,也即动能和内能之间的转化。Zheng和Bray[31]最早通过构造基于经验的平均温度修正公式以考虑超声速流动中动能向内能的转化。Sabel’nikov等[32]在此基础上根据条件平均的思想,引入了速度关于混合分数的条件平均,从而将动能变化对火焰内部结构的影响包含到火焰面数据库中。以上两种修正模型中温度仍然采用火焰面数据库积分获得,无法有效考虑超声速流动中速度和温度的强耦合,故未得到广泛应用。Overmann[33]首次将火焰面模型应用于实际构型超燃冲压发动机燃烧室的二维数值模拟中,提出了仅利用火焰面数据库PDF 积分获得组分浓度,而温度由能量方程隐式得到的策略,使得基于低马赫数假设建立的火焰面模型可应用于复杂的超声速流动中。该策略之后被其他一些学者采用,包括基于火焰面模型的RANS模拟[34-36]以及LES模拟[37-40]。
然而,Overmann的策略在建立组分浓度的火焰面数据库过程中并未计及流动中的高马赫数可压缩效应,将基于该数据库获得的平均组分浓度直接用于反解温度的方法在理论上是不完备的。在高马赫数条件下分析1.1节中的火焰面模型理论:一方面,式(3)中将燃烧空间内的压强视为常数,而在超燃冲压发动机燃烧室流场中,由于存在复杂的波系,压强的空间变化明显;另一方面,式(2)中h 和Z 的线性关系在高马赫数流动中显然不能成立,此时动能变化引起的静焓变化将对火焰内部产生影响。
为了评估压强的空间变化在火焰面内部结构的影响,Gao等在文献[41]中针对德宇航(DLR)的超声速燃烧室[27]内典型流动条件(如表1所示),在不同的p0值(1~1.6)×105Pa条件下求解了火焰面方程(1~3),结果由图2 给出。可以看到,在基准压强1×105Pa基础上增大60%后,混合分数空间内的主要组分H2、O2和H2O 浓度变化非常小,且变化主要集中在Zst附近;而对于中间产物H、O 和OH 等,图2中显示压强变化可诱导出较明显的变化。接下来,将压强值取1.6×105Pa时获得的火焰面数据库用于DLR 的燃烧流场模拟,与之前使用基准压强火焰面数据库所获得温度结果进行了对比,如图3所示。可以看到,之前p 取1×105Pa火焰面数据库获得的温度峰值低于p 取1.6×105Pa时火焰面数据库的结果,但误差在3%以内。可以预想,若生成火焰面数据时采用的压强值高于实际燃烧流场压强值时,所获得的温度结果将偏低。

表1 DLR 超声速燃烧室实验算例条件Table 1 Experimental conditions for DLR scramjet

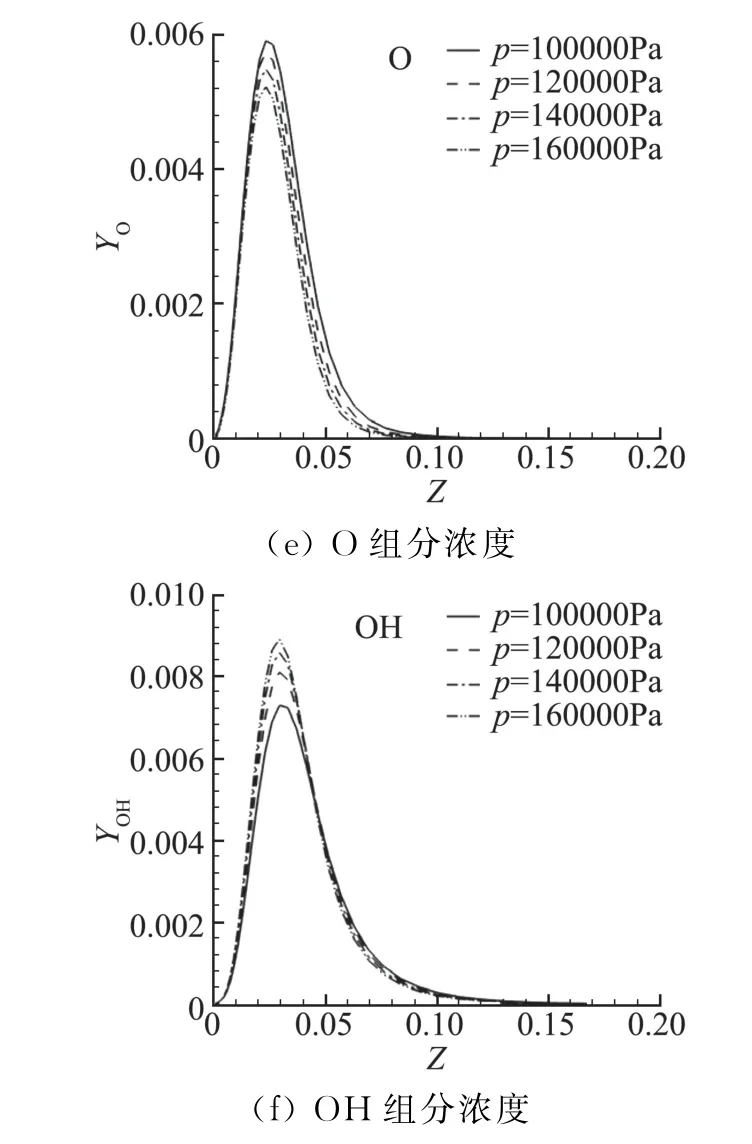
图2 不同压强取值条件下求解火焰面方程获得的组分浓度对比Fig.2 Species mass fraction distributions in the Z space under different values of p
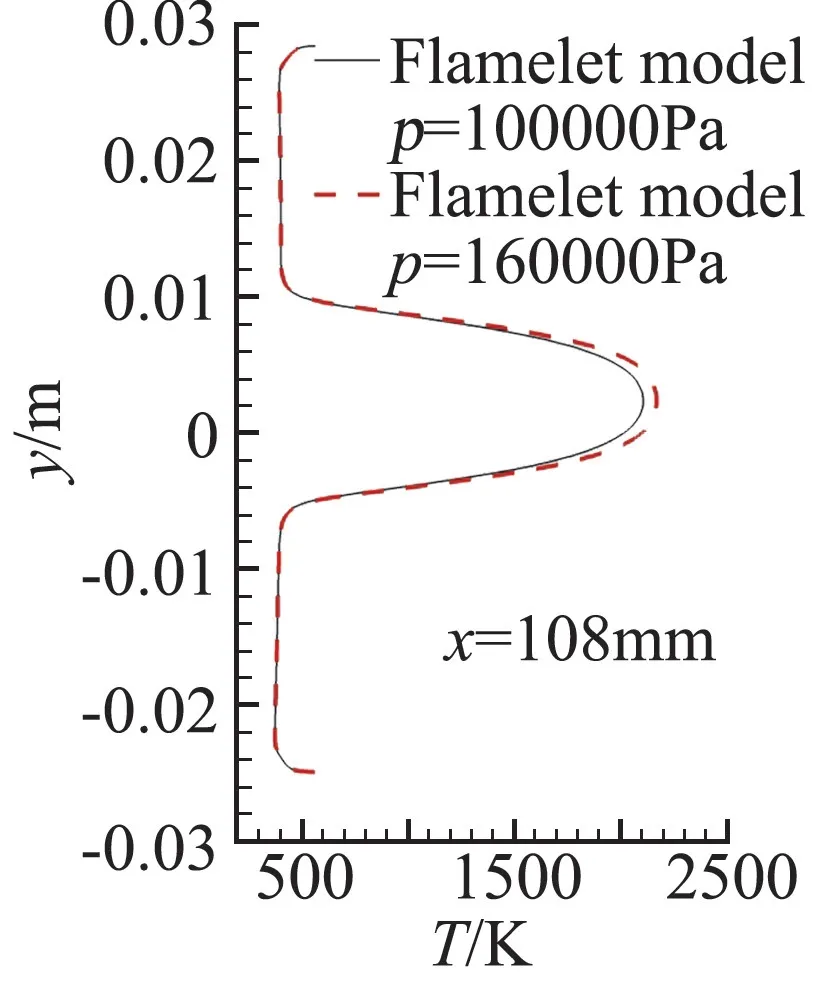
图3 不同压强取值条件下求解火焰面方程获得的温度分布Fig.3 Temperature distributions obtained by different sets of flamelet library with different values of p
以上的研究发现,火焰面数据库中的主要组分浓度以及所获得的流场温度对数据库建立时给定的环境压强取值并不敏感,在实际应用时可以选择燃烧室内的典型压强值作为火焰面数据库建立时的环境压强值。然而,若关心中间产物的浓度,则环境压强的取值则会产生明显影响。还有一点需要说明,如果实际燃烧室内的压强变化范围很大,则压强的变化也会对数据库中的主要组分浓度产生显著影响,此时则需要在火焰面数据库中考虑压强的影响。

图4 DLR 燃烧室内的温度云图Fig.4 Temperature contour in the DLR combustor
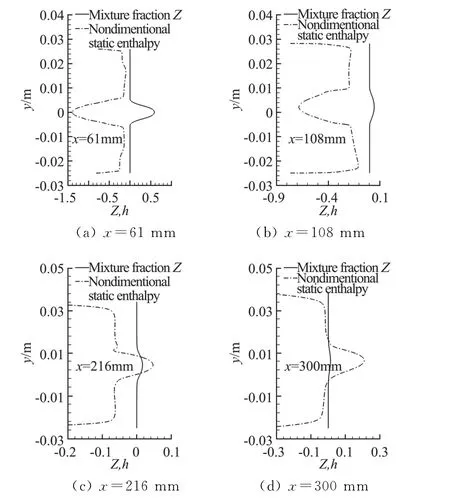
图5 燃烧流场中不同站位的平均 和的分布对比Fig.5 Distributions of andat different streamwise locations
另一方面,分析高马赫数可压缩效应在火焰面方程中的另一个重要影响:式(2)中的瞬时静焓h 与混合分数Z 的线性关系将不再成立。Gao 等在文献[41]中利用DLR 燃烧室流场定量评估了这一误差的影响。首先,提取了DLR 燃烧室流场(如图4所示)不同流向站位上的、用空气来流和氢气射流静焓值无量纲化后的分布,见图5。若瞬时的Z 和h满足线性关系,则应与相等,但图5中显示,不同站位上可以发现两条曲线差别明显,说明Z 和h的关系严重偏离线性关系。要定量评估这一误差的大小,需要在火焰面模型方程中建立真实的瞬时h和Z 的关系,进而建立相应火焰面数据库,将计算的温度结果与之前的结果对比。然而,超声速流动中瞬时h 和Z 关系并无确定的理论形式,因此以上做法无法实现。Gao等借鉴了Sabel’nikov等[32]提出的h 和Z 的二次函数关系。除了氧化剂和燃料来流确定的两个边界条件关系外,再提取每个站位上最大值与的对应关系,构造了不同站位上不同的h和Z 二次函数关系来生成不同的数据库。如图6给出了按以上方法获得的四个站位上的h 和Z 二次关系曲线。
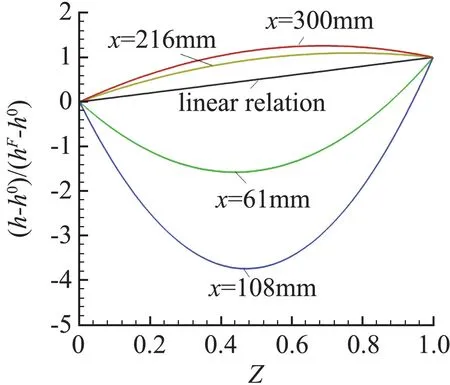
图6 不同站位上h 和Z 的近似二次函数关系Fig.6 Different h-Z quadric relations for different streamwise locations
图7 为不同的h 和Z 二次函数关系获得的火焰面数据库中典型组分(H2O 和OH)浓度在混合分数空间内的分布,可以看到主要组分的浓度差别很小,而中间产物浓度则有明显不同。应用以上火焰面数据库分别获得不同站位上的温度分布(记为flamelet model h-Z),并与之前的温度结果进行对比,如图8所示。可以看到,虽然图5中显示由于可压缩效应导致的与的偏离非常大,但图8中的数值实验结果却显示此偏离所引起的火焰面模型获得的温度差别非常小,温度峰值的偏差最大约为0.5%(x=108 mm)。特别地,x=108 mm 站位上,flamelet model h-Z 得到的温度峰值低于火焰面模型结果,表明在动能向静焓转化的流场区域未考虑可压缩效应的火焰面模型获得的温度场将偏高;x=300mm 站位上,flamelet model h-Z 得到的温度峰值均高于火焰面模型结果,表明在静焓向动能转化的流场区域未考虑可压缩效应的火焰面模型获得的温度场将偏低。由此可见,式(2)中h 和Z 线性关系在超声速流场中误差很大,但该效应对于火焰面模型温度场的模拟的影响很小。

图7 不同的h 和Z 关系下求解火焰面模型方程获得的组分浓度分布Fig.7 Mass fraction distributions in the Z space obtained under different h-Z relations
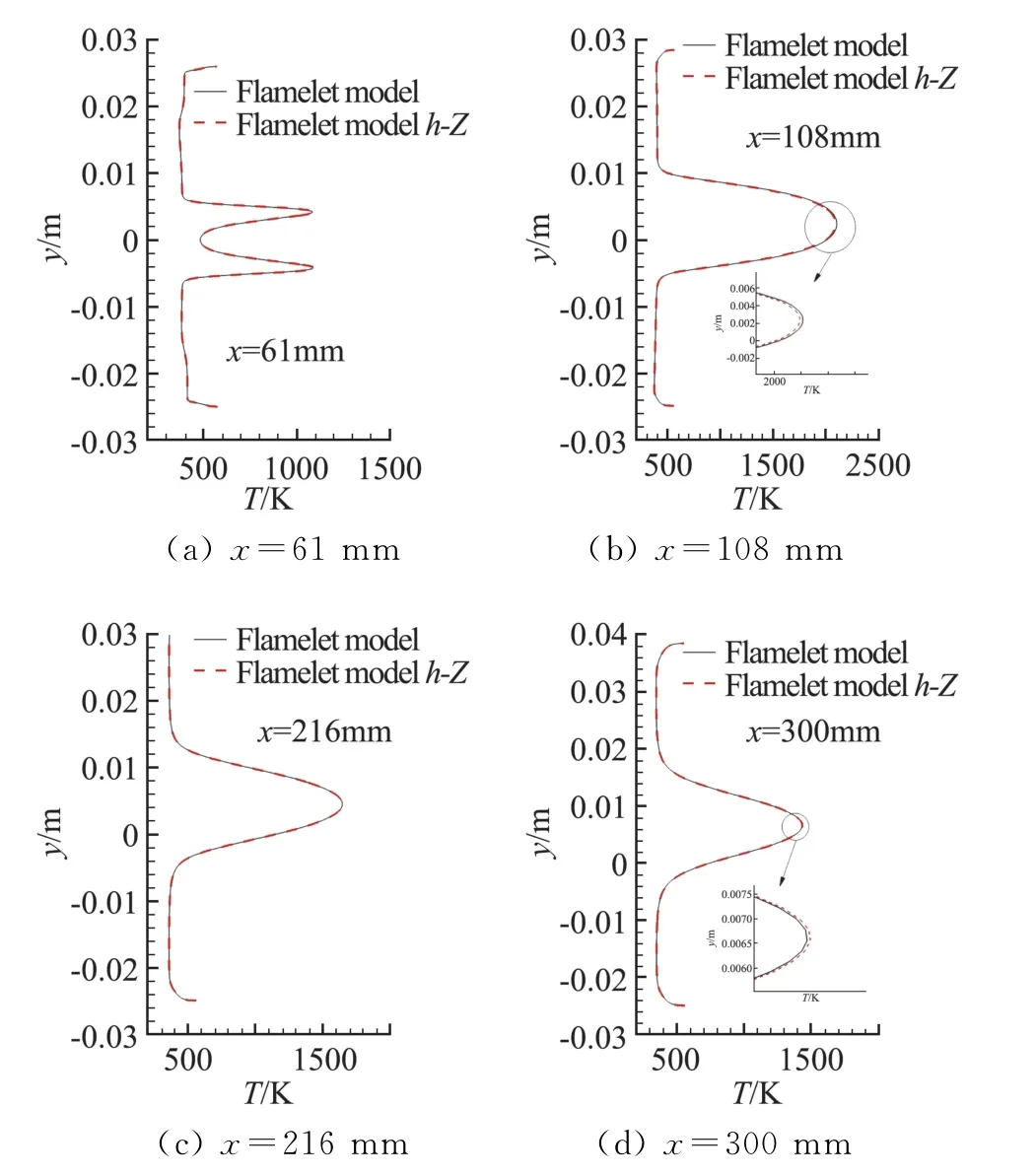
图8 考虑动能与静焓相互转化后的火焰面模拟获得的温度分布Fig.8 Temperature distributions using different sets of flamelet library under different h-Z relations
为了进一步评估流场可压缩效应对火焰面模型模拟的影响,高振勋等[42]建立了一种交互式的火焰面模型(Representive Interactive Flamelet model,RIF),即将流动方程与火焰面方程耦合求解,通过为燃烧区域的每点建立与当地流场参数相匹配的火焰面数据库,将流场当地压强变化以及h-Z 关系的变化直接引入到火焰面数据库中。利用RIF 模型对DLR 燃烧室的计算结果表明在该算例条件下,其与传统火焰面计算结果差别很小,表明该流动中可压缩效应对火焰面模型模拟结果影响很小。
3 火焰面/进度变量模型的可压缩修正
火焰面/进度变量模型所采用的数据库中包含了组分浓度和进度变量化学反应源项数据,该模型应用于超声速流动除了要考虑上文中流场当地的可压缩效应对数据库中组分浓度的影响,还需要考虑进度变量化学反应源项受可压缩效应的影响。Saghafian等[43]展示了火焰面数据库中的进度变量化学反应源项值对于混合分数空间内静焓分布变化非常敏感,因此在超声速流动中使用火焰面/进度变量模型时必须对数据库中化学反应源项进行可压缩修正。由于火焰面/进度变量数据库的建立很复杂,因此在建立数据库的过程中考虑流场当地可压缩效应非常困难。Saghafian[43]提出了另外一种思路:在建立数据库的时候仍然采用给定的压强值和静焓分布,而对PDF积分后的进度变量源项值构造基于流场当地变量的可压缩标度,其提出的可压缩标度形式为:
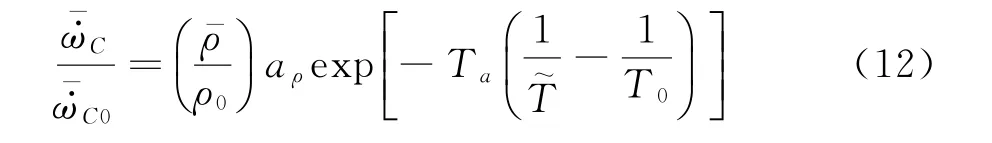

高振勋等将其提出的可压缩火焰面/进度变量模型应用于Cheng 的超声速轴对称射流燃烧实验算例[44]的RANS模拟,其温度场结果如图9所示。

图9 FPV模型所得Cheng算例的温度场Fig.9 Temperature contour using FPV model for the Cheng case

图10 式(13)可压缩标度系数沿对称轴的分布Fig.10 Distributions of the rescaling coefficient by Eq.(13)along axis
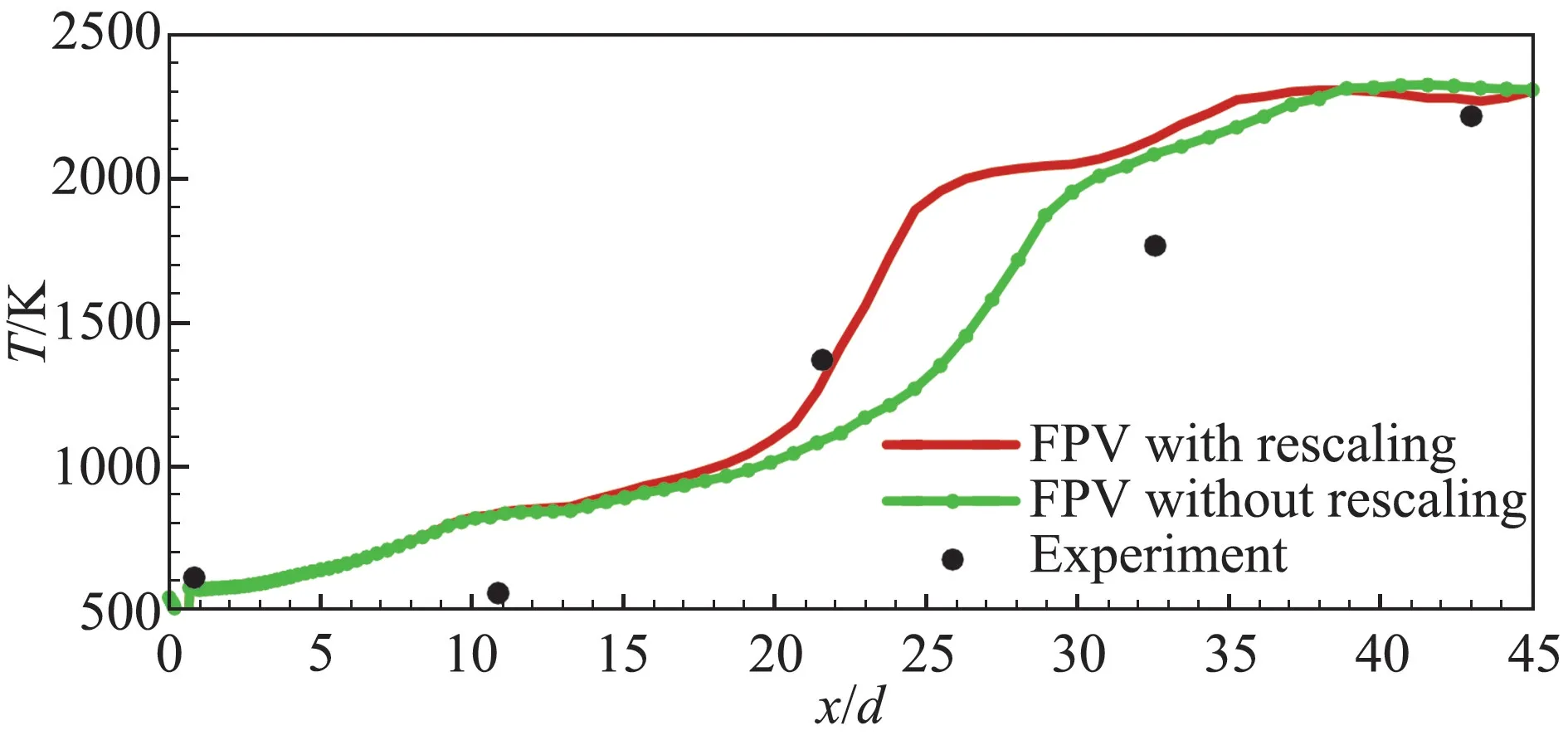
图11 使用/不使用可压缩标度的FPV模型得到对称轴温度分布对比Fig.11 Distributions of the temperature along axis using FPV model with and without the compressible rescaling
图10 展示了利用式(13)计算得到的进度变量源项可压缩修正系数在对称轴上的分布,可以看到,该系数在大部分区域均大于1,表明流场中可压缩效应显著增大了进度变量的化学反应源项。图11给出了使用式(13)可压缩标度的火焰面/进度变量模型与不使用该修正所得到的对称轴上温度分布对比,与图11中的结果相对应,式(13)的修正通过增大进度变量的源项从而所得到点火位置也提前,也与实验数据更加吻合,初步展示了该可压缩标度的有效性。该可压缩修正在复杂超声速燃烧流动中模拟的可靠性还待进一步开展研究。
4 结 论
本文主要针对火焰面模型以及火焰面/进度变量模型应用于超声湍流燃烧流动中所开展的可压缩修正相关研究进行了综述,主要研究结论包括:
1)对于火焰面模型,其数据库建立时压强为常数以及静焓与混合分数线性关系的假设在超声速流动中均不成立。数值实验发现:数据库中主要组分浓度对于压强的变化并不敏感,因此所获得的流场平均温度也与建立数据库所给定的压强值不敏感;虽然静焓与混合分数的关系在超声速流动严重偏离线性关系,但这一点引起的火焰面模型获得的温度场差别却很小。因此,尝试为流场每点建立考虑可压缩效应的数据库的交互式火焰面模型,与传统火焰面模型模拟的结果差别较小。
2)火焰面/进度变量模型数据库中进度变量的化学反应源项对于压强和静焓-混合分数关系的变化很敏感,现有考虑这一影响的可压缩修正主要是通过针对利用未经修正的数据库PDF积分后的平均源项进行可压缩标度来实现。数值实验研究发现,可压缩标度方法可有效考虑高马赫数效应对进度变量源项的影响,从而改善火焰面/进度变量模型对超声速燃烧流动的模拟精度。
