计及需求响应的风电并网优化研究
2020-11-03马涛
马 涛
(郑州轻工业大学 电气信息工程学院,郑州450002)
随着能源短缺和环境污染问题的日益严峻,开发清洁可再生的新能源受到人们的广泛关注和重视,其中风力发电因清洁高效等优良特性而获得快速发展[1],分布式风电在配电网的渗透率越来越高,但分布式风电输出功率具有典型的波动特性,为保证配电网的安全稳定经济运行,配电网对分布式风电的消纳能力是有限的,弃风现象在配电网的运行中时有发生[2],因此,为促进风电新能源的利用效率和配电网安全经济性的提高,需对风力发电在配电网的并网进行优化分析。
针对风力发电的并网优化,相关学者进行了一定的研究。 文献[3]建立以经济性为目标的风电并网优化模型,采用遗传算法对风电并网模型进行优化,文献[4]以风电并网后配电网运行总成本最低为优化目标,采用粒子群法进行风电并网优化,虽然均取得了一定的优化效果,但随着风电规模的增大,单纯依靠供应侧来满足配电网的安全经济运行变得日益困难,而需求响应通过对电力用户消费模式的改变,可使用户用电行为更贴近新能源输出功率特性,从而提高电网的消纳能力和风电的利用效率。 文献[5]对需求侧响应的政策、标准及实践现状进行了阐述,表明了需求响应的意义。 文献[6]在进行配电网资源规划时将需求侧响应考虑在内,分析了需求响应对配电网经济规划的影响,表明需求响应能更好地提高配电网的经济性。
本文在对风电输出功率特性分析的基础上,考虑需求响应对风电并网优化的影响,建立了计及需求响应的风电并网优化模型,模型的求解则采用Q 学习算法和量子粒子群法相融合的求解方法,通过PJM5-bus 配电网系统风电并网优化实例的计算分析,表明了本文优化模型及求解方法的有效性和优越性。
1 风电输出功率特性分析
风力发电机的有功输出功率Pw主要与风速v相关[7]:

式中:vci、vco为风力发电机的切入风速、切出风速;Pr、vr为额定功率、额定风速。
根据相关研究发现,某地区的风速服从Weibull分布[8],则可得风力发电机有功输出功率的概率密度函数为
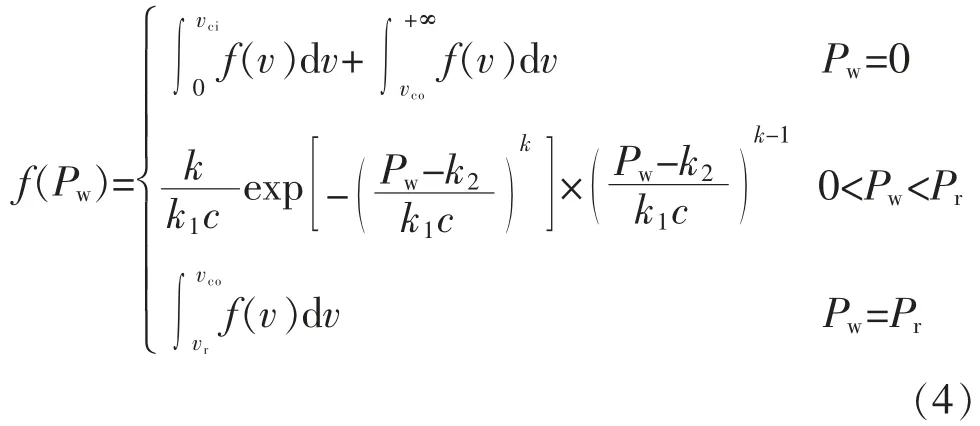
式中:k、c 为Weibull 分布函数的形状参数和尺度参数。
风力发电机多采用双馈式,定子绕组与电网为直接相连,转子绕组则由PWM 与电网相连,其定子侧和网侧变流器均能发出一定的无功功率[9],定子侧变流器无功功率下限、上限的表达式为
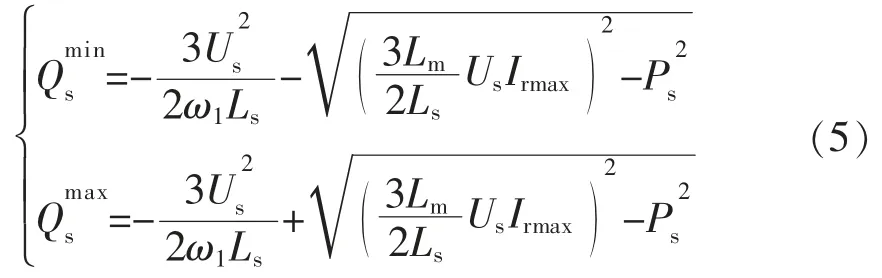
式中:Ps、Us、Ls分别表示定子有功功率、定子电压峰值和定子电感;Lm表示定子与转子的互感;Irmax表示转子侧变流器的最大电流;ω1表示定子电流角频率。
网侧变流器无功功率Qw的上下限范围为
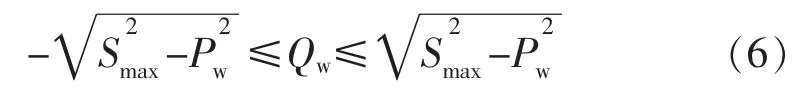
式中:Smax表示网侧变流器设计的最大功率;Pw为输出的有功功率。
综合式(5)和式(6)可得双馈式风力发电机的无功功率下限、上限的表达式为
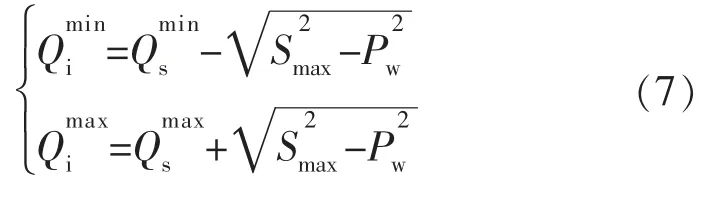
2 风电并网优化数学模型
2.1 目标函数
需求响应是指根据电价的引导或其它激励机制,使电力用户改变固有的用电模式的供需互动形式,通过需求侧响应可使电力用户的用电行为更贴近新能源的功率输出[10]。 本文在风电并网优化时计及需求响应主要是通过改变可转移负荷的使用时间,使负荷与风力发电在时序上更加贴近,从而促进风电消纳,缓和风电的波动,并提高电网的经济性。
本文可转移负荷模型表达式为[11]

式中:SLin(t)、SLout(t)表示t 时段可转移负荷转入总量、转出总量;NSL、NSLa分别表示可转移负荷的种类总数和运行时间大于一个时段的可转移负荷种类总数;Ik(t)、Ok(t)分别表示第k 类负荷在时段t 的转入量和转出量;pi,k表示第k 类可转移负荷在时段i的功率值,k 的取值范围为[0,NSL]。
本文计及需求响应的风电并网优化目标为完整调度周期内的电网经济性最好,目标函数表达式为
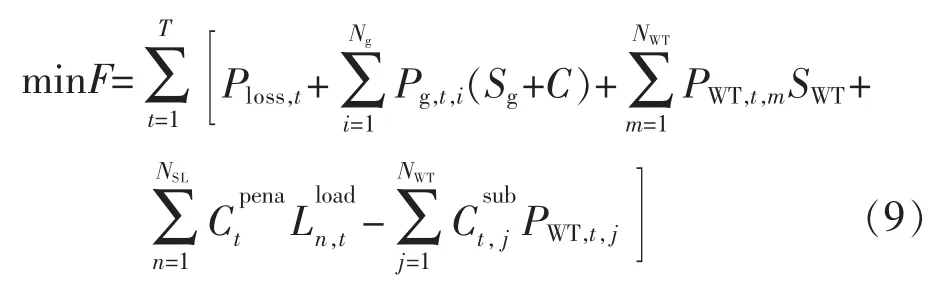
式中:T 表示完整调度周期的时段总数;Ng、NWT分别表示火力发电机组和风力发电机的数目;Ploss,t表示t 时段风电并网网络的损耗成本;Pg,t,i表示t 时段火电机组i 的发电功率;Sg、C 分别表示火电机组发电成本及环境成本;PWT,t,m表示t时段风机m的发电功率;SWT表示新能源风力发电的成本;表示第n个用户在t 时间 的可转移负荷量;、分别表示转移负荷在时间t 的补偿成本和风力发电的补贴价格。
2.2 约束条件
对风电并网进行优化需满足一定的等式约束条件和不等式约束条件。
等式约束条件表达式为
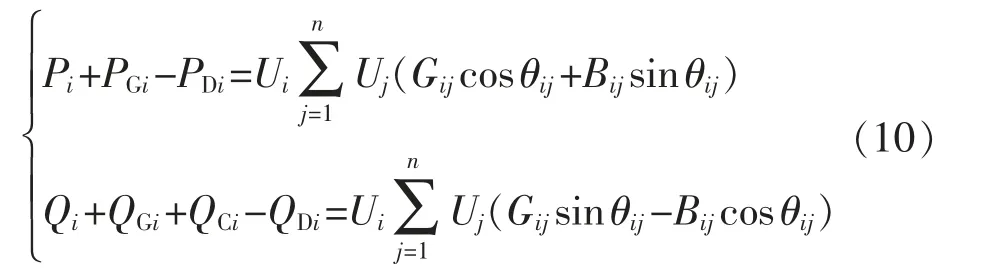
式中:Pi、Qi分别表示注入节点i 的有功功率和无功功率;PGi、QGi分别表示节点i 风力发电机输出的有功和无功功率;PDi、QDi分别表示节点i 的有功负荷和无功负荷;QCi表示补偿电容器输出的无功功率;Ui、Uj分别表示节点i 和节点j 的节点电压;θij、Gij、Bij表示节点i 和节点j 之间的相角差、电导和电纳。
不等式约束条件的表达式为
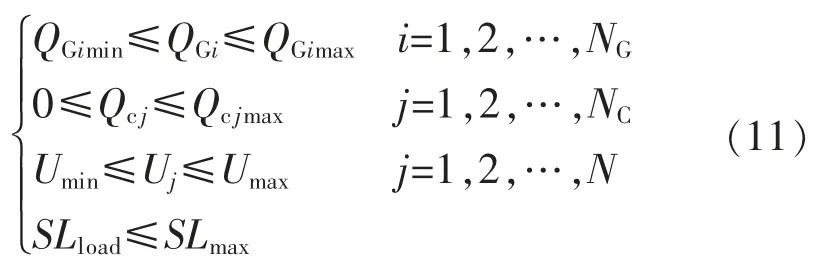
式中:QGi、QGimin、QGimax为风力发电机输出的无功功率及其最小值和最大值;QCj、QCjmax为无功补偿装置的无功输出及其最大值;Uj、Umin、Umax为节点电压及其最小值和最大值。
3 量子粒子群与Q 学习融合法原理
粒子群算法是一种基于鸟类觅食行为的群体智能优化算法[12],它通过对自身位置的不断更新来获得全局最优解,算法中的每个粒子均为优化目标的一个可能解,粒子的特征指标包括位置、速度和适应度值,传统粒子群法的速度和位置更新表达式为

式中:Vid、Xid分别表示粒子的速度和位置;k 表示迭代次数;c1和c2表示学习因子;ω 表示惯性权重;r1和r2为[0,1]之间的一随机数;Pid、Pgd表示粒子算法当前的个体最优值和全局最优值。
为克服粒子群算法全局性不足的缺点,研究人员将量子理论引入粒子群算法,提出了量子粒子群优化算法[13]。 量子粒子群优化算法只对位置进行更新,减轻了算法的复杂度,提高了算法的计算效率。量子粒子群法的进化方程表达式为

式中:Pi(t)表示局部吸引子;Pid(t)表示个体最优位置;Pgd(t)表示全局最优位置;M 为种群的粒子数;mbest(t)表示算法的平均最优位置;α 表示扩张收缩系数;Xi(t+1)表示t+1 时刻粒子的位置信息;φ 和u表示区间(0,1)的随机数。
参数α 是量子粒子群算法的唯一控制参数,通过α 的调节能够控制算法的搜索性能和收敛速度。根据强化学习方法的启发,可将Q 学习方法引入到量子粒子群算法中,其行动则为参数不同的选择策略,个体选择最优参数策略就转化为代理选择最优行动,在算法的搜索过程中,通过选择最优的行动参数来控制算法的搜索。
Q 学习算法是一种与问题模型无关的典型强化学习方法[14],它通过选择最大化代理带折扣的累积收益的行动来获得代理的最优行动策略。 智能体在每个状态均会依据自身策略来选择一个动作到达下一个状态,并将此动作的评价结果反馈给智能体,智能体则基于反馈信息来调整原有的策略,从而获得最优的动作。 Q 学习算法在t 时刻选择动作αt的评价值设为Q(st,αt),st表示算法的状态,则Q矩阵更新表达式如下所示:

式中:rt表示t 时刻的即时反馈结果;σ 表示学习因子,取值范围为0<σ<1;γ 表示折扣因子,取值范围为0<γ<1;st+1表示Q 学习算法下一个时刻的状态。
在量子粒子群算法中将群体中的粒子看作Q学习方法的代理,扩张收缩系数α 的选择策略等效为代理行动的集合,从而实现Q 学习方法与量子粒子群法间的映射。 本文融合量子粒子群法和Q 学习方法的求解方法基本流程如图1所示。

图1 本文融合算法基本流程Fig.1 Basic flow chart of fusion algorithm in this paper
4 风电并网优化算例分析
4.1 系统算例
本文以PJM5-bus 配电网系统作为测试系统进行相应的计算分析[15],分布式风力发电场接入节点1,系统结构如图2所示。 系统负荷分布于节点2、3、4,负荷比为3∶3∶4,机组G1、G2、G3、G4、G5 为常规火电机组,额定容量分别为100 MW、110 MW、520 MW、200 MW、600 MW,典型日下的系统负荷曲线和风力发电场的输出功率曲线如图3所示。 弃风惩罚成本为55 元/MW·h,高峰时间段的负荷节点2、3、4 的可转移负荷量及对应的转移成本、响应成本如表1所示。
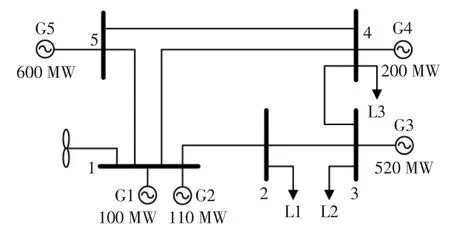
图2 PJM5-bus 配电网系统Fig.2 PJM5-bus distribution network system

图3 典型日下功率曲线图Fig.3 Typical daily power curve
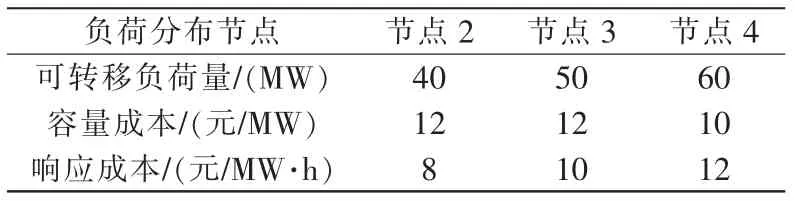
表1 可转移负荷参数表Tab.1 Transferrable load parameters
4.2 优化结果分析
根据本文建立的风电并网优化数学模型,对图2所示的测试系统进行并网优化,采用遗传算法、粒子群法、退火粒子群法和本文提出的Q 学习与量子粒子群融合算法对不计及需求响应、计及需求响应下的并网模型做优化求解,表2为并网优化后的结果,图4为计及需求响应时四种优化算法的收敛过程曲线图。
由表2和图4的并网优化结果可知,在风电并网优化时,考虑需求响应要比不考虑需求响应的并网总成本更低,配电网运行的经济性更好,弃风率更小,风电可获得更高得渗透率,与遗传算法、粒子群法、退火粒子群法相比,本文提出的Q 学习与量子粒子群融合算法在风电并网模型优化过程中能获得更好的优化结果,优化后获得的并网总成本为1153265.22 元,在四种算法中是最低的,且本文融合算法具有优良的收敛特性,优化时间仅比陷入局部最优解的遗传算法更慢,寻优过程收敛较快。
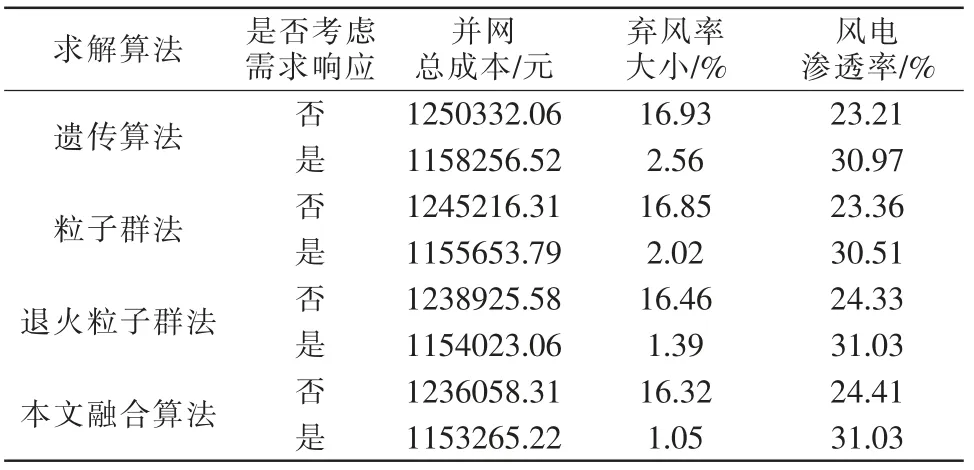
表2 并网优化结果分析Tab.2 Analysis of grid-connection optimization results
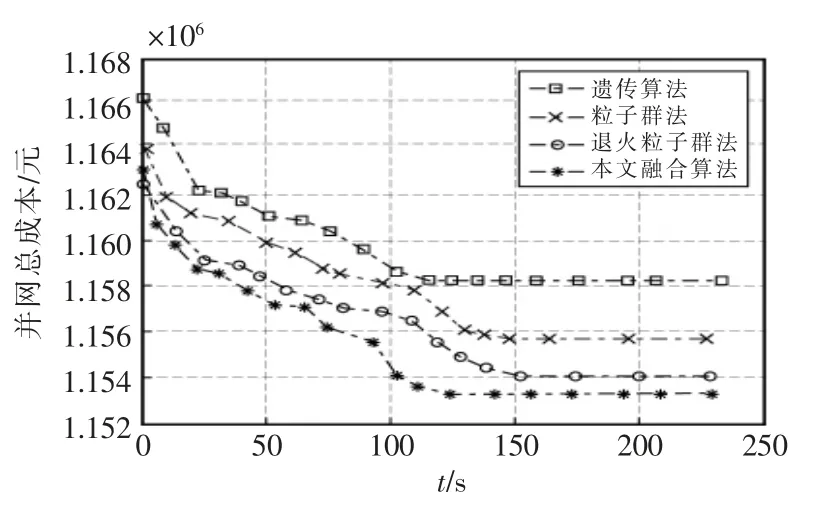
图4 优化收敛过程曲线图Fig.4 Optimize convergence process curve
5 结语
本文建立了计及需求响应的风电并网优化数学模型,并提出了Q 学习与量子粒子群相融合的求解算法,通过风电并网优化实例的计算对比分析,结果表明考虑需求响应的方法可使配电网负荷更好地响应风电的输出功率特性,从而获得更低的并网总成本、更低的弃风率和更高的风电渗透率,提高配电网的经济效益及对风力发电的消纳能力,而本文提出的Q 学习与量子粒子群相融合的求解方法能得到更好的优化解,优化后的风电并网总成本达到最低,且本文求解方法具有优良的收敛特性,优化所需时间较短。
